弯矩调幅法在连续梁计算中的研究

李 凯

(新疆水利水电勘测设计研究院,新疆 乌鲁木齐 830000)



弯矩调幅法在连续梁计算中的研究

李 凯

(新疆水利水电勘测设计研究院,新疆 乌鲁木齐 830000)

为了更好的解决厂房中楼梯内力计算值与实际值存在的差异,尽可能消除不合理的因素,引入了弯矩调幅的有限元计算法,对内力计算的弯矩值进行调整。本文阐述了弯矩调幅法的理论依据,并通过实例算例验证了该方法计算的可行性与合理性。最终计算结论说明：弯矩调幅系数与跨中弯矩值的调整值成线性关系,调整的幅度与外荷载以及结构支座的性质有关,弯矩调幅系数的选取受到结构塑性铰范围内的制约。

弯矩调幅法；连续梁内力计算；塑性铰；相对受压区高度

厂房设计中,楼梯是设计中经常出现的结构,但不同于普通的建筑专业,工业厂房和水电站厂房中,某些部位的楼梯不仅作为主要的交通通道,同时还往往会运输某些重要设备,所以，规范中荷载较大,按照普通的方法进行计算和控制往往使得截面和配筋量增大。因此，根据超静定钢筋混凝土结构的非弹性的理论[1-2],对结构内力计算的方法采取内力重分配,尤其是对结构弯矩根据塑性设计原理进行适当降低,在满足结构安全的前提下认为进行控制是解决问题的有效方法。

1 弯矩调幅与问题的提出

对于厂房的楼梯结构,无论是板式还是梁式楼梯,往往都是超静定结构,其一侧有较厚的墙体支撑,同时，两端也有厚板结构或柱挑出的梁系结构作为支座,此时按照理想的线弹性模型计算这些结构连接处就是刚性节点,即假设结构在受力过程中变形不变,这样会加大支座处的负弯矩值,同时钢筋过密又会增加施工难度,不利于混凝土的浇筑。尤其是对于连续梁计算,传统的内力计算方法往往有其局限性[3]。

基于上述考虑,为了追求和模拟与实际更加相符的受力条件,同时改善支座部位钢筋过于密集的状况,便于混凝土浇注,引入弯矩调幅的方法是合理且必要的。 因为这样可以反映出结构在荷载作用条件下弯矩的重分配问题并加以解决[4]。

2 基于连续梁的弯矩调幅法的理论依据

对于楼梯结构一般由休息平台板和楼板组成,在荷载作用下,各个部位的内力在竖向投影上是一致的,因此空间结构的楼梯结构可以用水平方向的连续梁等效替代,计算简图见图1：

图1 楼梯结构内力等效模型的建立

根据有限元的平衡方程：

{K}{α}={P}

(1)

式中 {K}为楼梯节点的刚度矩阵；{α}为楼梯节点的位移矩阵；{P}为楼梯节点的力的矩阵。

对于楼梯的支座弯矩,当为正时则不进行调幅；当出现负弯矩时根据经验选取合适的调幅系数进行调幅,调幅后支座弯矩值为：

ML=MPP

(2)

式中ML为楼梯单元节点调幅后支座弯矩值；MP为 楼梯单元节点调幅前支座弯矩值；P为楼梯支座弯矩调幅系数。

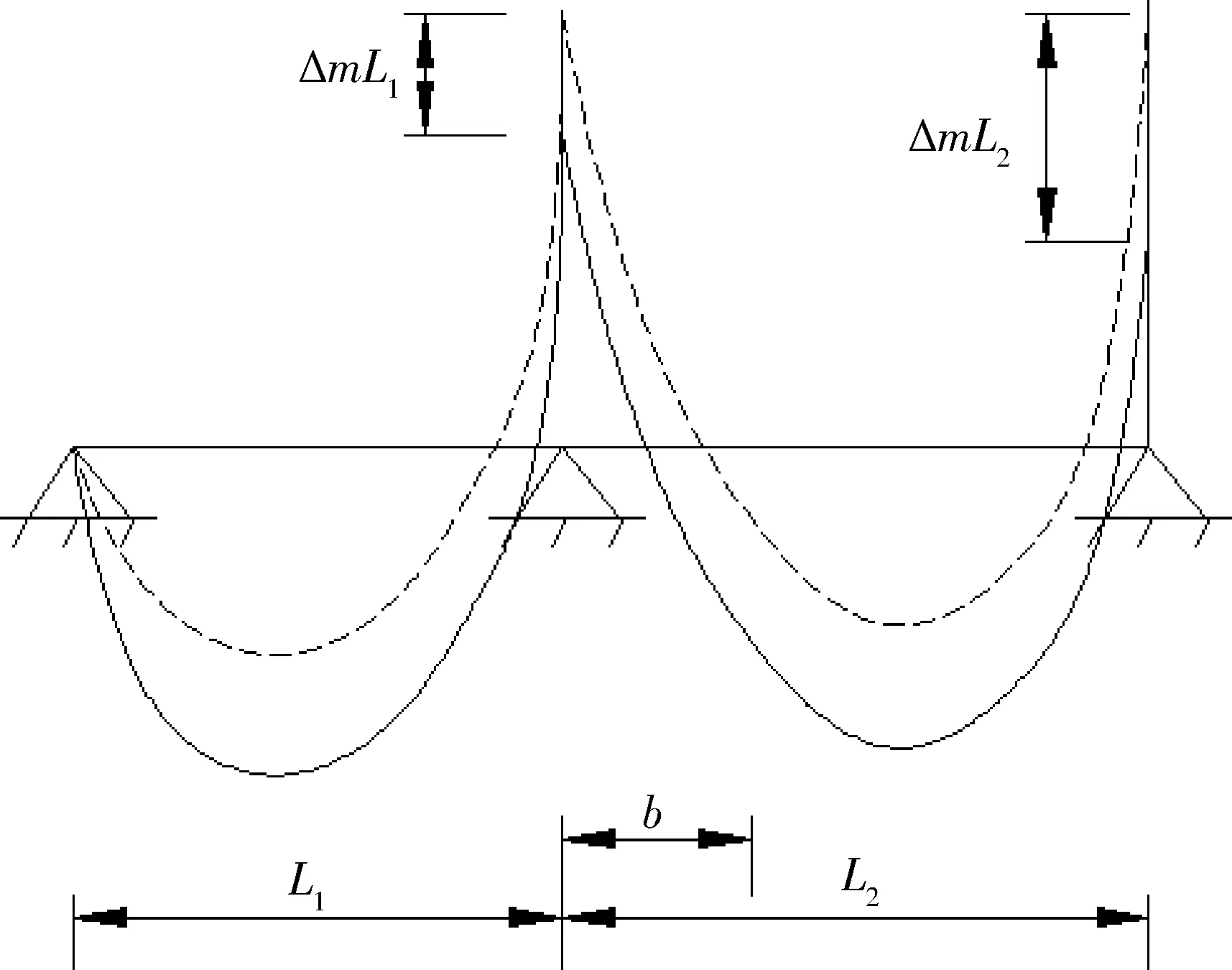
图2 楼梯结构弯矩调幅示意

对于连续梁根据弯矩调幅的含义,对于图2有如下关系：

ΔML1=MP1(1-p) 或ΔML2=MP2(1-p)

(3)

式中 ΔML1、ΔML2为楼梯左、右侧支座的弯矩调幅值；ML1、ML2为楼梯左、右侧支座的原有弯矩值。

在楼梯梯段的弯矩传递中,弯矩调幅沿程的变化量可以表示为：

(4)

即弯矩调幅沿程的变化就是表示两条曲线之间距离随长度的函数关系,也即楼梯梯段的导数表达式。

根据工程经验可知,在剪力线性分布的条件下进行计算可以满足精度要求,则此时在楼梯梯段的中间任意一个节点,把梯段L1和L2代入,当节点位于距离支座左端b时,任意节点的弯矩调幅值为：

(5)

实际计算中,不必任意一个截面的节点都需要计算,只需计算跨中截面的即可求得非支座节点的最大值,因此上面的公式也是跨中断面弯矩调幅的计算公式。

根据连续梁弯矩调幅法的规定,调幅后梁端支座弯矩绝对值的平均值加上跨中弯矩之和,应不小于按照简支梁计算的跨中弯矩值,即满足：

(|(ΔML1+MP1)|+|(ΔML2+MP2)|)/2+ΔML≥M0

(6)

式中M0为楼梯按照简支梁计算的跨中弯矩值。

总之,对楼梯梯段进行弯矩调幅,主要是考虑楼梯在承受一定的竖向荷载后,在梯段与平台板或支撑的邻近区域形成塑性铰之后,结构整体仍然在一定阶段具有一定的承载能力。但同时弯矩调幅也应该有一定限度,本文可以通过算例来验证这一点。

3 工程算例及成果分析

某水电站厂房的楼梯,混凝土材料强度为C25,选取其中一跑为计算对象,由梯段和休息平台板组成,结构两端各有支撑,其中梯段长度为5.2 m,休息平台板长为1.1 m,两端层高差为1.5 m,结构恒荷载取2 kN/m2,活荷载取8 kN/m2,梯板厚度为250 mm,对该结构进行弯矩调幅的计算分析,结构的计算简图见图3：

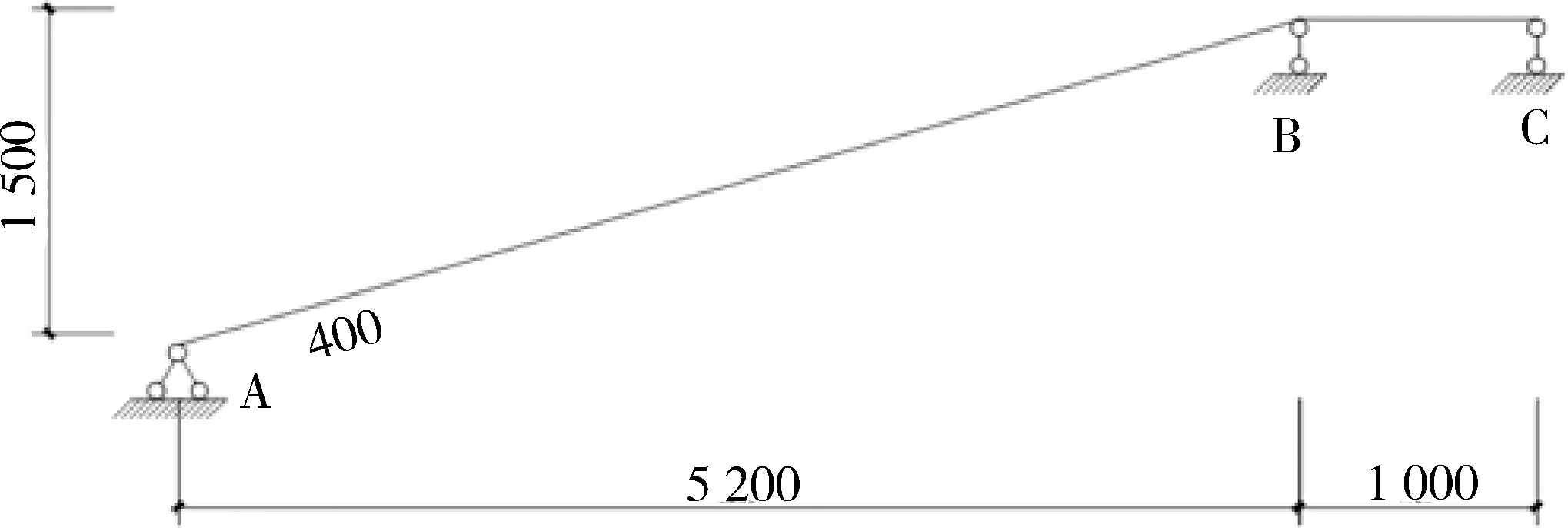
图3 楼梯算例结构示意(单位：mm)

根据以上的计算方法,采用有矩阵位移法对该梯段结构在P=5%，P=10%,P=15%,P=20%,P=25%几种调幅指标条件下的内力进行计算,最后计算结果见表1所示。

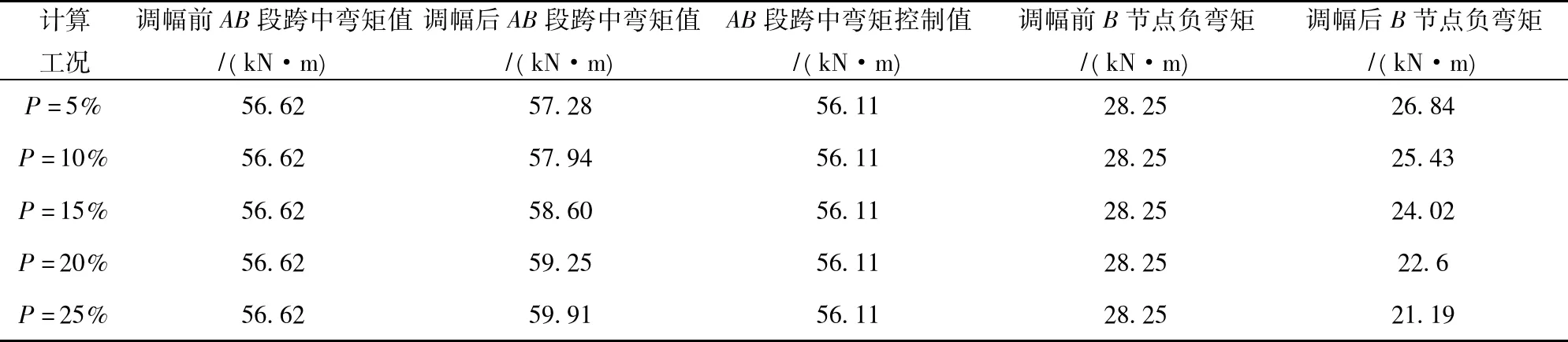
表1 不同调幅值条件下梯段弯矩有限元计算值

根据以上计算成果得到如下结论：

1) 在经过弯矩调幅法对有限元计算模型进行修正后,跨中弯矩值MAB相对于线弹性范围内有所增加,其增加值随调幅指标P的增加而增加,弯矩增加的幅度ΔML从1.17%变化到5.81%。与此同时,右端支座处的弯矩MB经过调幅的调整衰减迅速,减小的幅度值取决于弯矩调幅系数P的选取,计算结果达到了预期的效果和目的。

2) 把弯矩调幅系数P的变化率和跨中弯矩值MAB的变化率放在一张图标中进行比对,最后比对的结果见图4,发现二者的变化率呈线性分布,即证明了ΔML与ΔMAB具有线性相关的关系,二者的变化率ΔML/ΔL数值上等于下表直线的斜率,所以计算任意截面节点采取线性差值的方法进行计算是可行的。同时经过计算该直线的斜率约为0.232,经过计算验证该值与荷载分布和结构的计算简图以及支座的性质均有关系。

图4 不同调幅值条件下跨中弯矩值增大的变化趋势

3) 计算结果表明,虽然为了达到目的可以通过不断加大P值来消减支座处的弯矩,但也是有限度的,其原因就是混凝土结构塑性铰的转动是有限的[5],因此调幅量也是受此影响的,在弯矩调幅不宜大于25%的幅度内进行计算，可模拟梯段在塑性阶段的内力变形和弯矩的调整,再此基础上,楼梯梯段结构应满足正常使用极限状态的要求,即用裂缝开展宽度或挠度来控制结构是合理可行的。

4) 相关研究表明连续梁的调幅有其限值及其适用条件[6],计算时需要考虑混凝土的相对受压区高度ξ,当ξ>ξb时属超筋破坏,此时受压区混凝土已经破坏,结构不会形成塑性铰,因此，其值的大小反映了塑性铰的转动能力,这也是计算中的边界条件。

针对这种情况,对不同指标条件下的相对受压区高度ξ进行计算,计算成果见表2,在荷载值相对较低的条件下,相对受压区高度ξ均处于较低水平,均小于最大允许值(对C25混凝土,ξb取0.544),结构均可以形成塑性铰,且安全余地较大,前面的内力计算值真实有效。

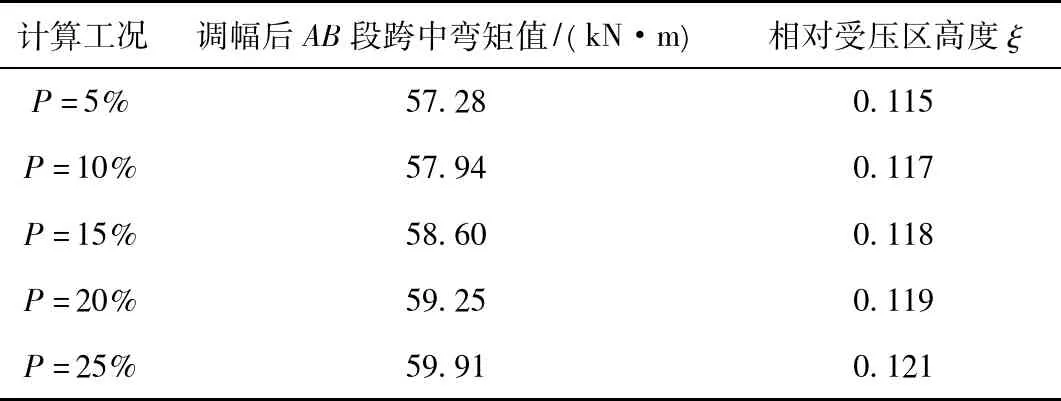
表2 不同调幅值条件下相对受压区高度的变化趋势

由于在荷载不大的条件下相对受压区高度随弯矩的变化率不大,这样会导致增加钢筋的配筋率,从而减小塑性的转动能力[7],因此，实际工程中可适度考虑调整支座截面的约束条件以解决这一问题。

4 结语

根据计算与分析可知,弯矩调幅法具有充分发挥结构承载力、减小支座截面配筋的特点,体现了内力分析与截面设计相协调的理念,尤其应用在连续梁内力计算结果与配筋量的调整与优化上具有主要意义,该计算方法的优越性和可靠性经过了对比和验证。在具体计算与设计中,需要重点判断结构处于塑性状态的范围,从而确定调幅的指标和区间,有必要时需对弯矩调幅后结构的抗剪能力需要重新复核。计算发现,荷载的水平应与弯矩调幅系数相匹配,有关的取值范围极其理论依据还有待继续深入研究并需要更多工程实例的验证。

[1] 过镇海.钢筋混凝土原理[M].北京：清华大学出版社, 1999．

[2] 河海大学,武汉大学,大连理工大学. 水工钢筋混凝土结构学(第四版)[M]. 北京：中国水利水电出版社，2009.

[3] 陈叶文,马博.利用mathcad及力法原理计算多跨连续梁的内力[J]. 广东水利水电， 2015 (8)：1-3，10．

[4] 屈凯锋.竖向及水平荷载作用下后张预应力框架的试验研究[D].重庆：重庆大学, 2002 ．

[5] 杨春峰,郑文忠,于群.钢筋混凝土受弯构件塑性铰的试验研究[J]. 低温建筑技术， 2003(1)：38-39．

[6] 邓宗才. 钢筋混凝土连续梁弯矩调幅法的研究[J] . 建筑结构， 1997(8)：30-32．

[7] 常莹莹. 钢筋混凝土受弯构件的延性分析[D] . 大连：大连理工大学, 2011 ．

(本文责任编辑 王瑞兰)

The Bending Moment Amplitude Modulation Method on research of Continuous Beam Calculation

LI kai

(Xinjiang Water Conservancy and Hydropower Survey Design Institute , Xinjiang, Urumqi)

in order to better solve the stairs in workshop internal force calculation value and actual value differences, eliminate the unreasonable factors, the introduction of the bending moment amplitude modulation of the finite element method, to adjust the bending moment of internal force calculation value. It is expounded in this article, the theoretical basis of the bending moment amplitude modulation method and through the instance example verifies the feasibility and rationality of the method. Final calculation conclusion: bending moment amplitude modulation factor and across a linear relationship with bending moment value adjustment, the adjustment range and the external load and the nature of the support structure, bending moment amplitude modulation factor selection is restricted by the structure within the scope of plastic hinge.

the bending moment amplitude modulation method; Continuous beam internal force calculation; The plastic hinge; The relative compressive zone height

2016-01-13;

2016-02-24

李凯(1982),男,硕士,工程师,从事水工结构设计工作。

TU323.3

A

1008-0112(2016)01-0041-03