V形导流伞对大型球罐热处理温度场的影响研究*

吉 方 邓贵德 梁海峰 段滋华

(1.太原理工大学；2.中国特种设备检测研究院)

V形导流伞对大型球罐热处理温度场的影响研究*

吉 方*1邓贵德2梁海峰1段滋华1

(1.太原理工大学；2.中国特种设备检测研究院)

用内燃法热处理大型球罐时，为了减小球罐上下的温差，在球罐内部加入一个V形导流伞，改变球罐内流场分布，使热空气对球罐加热更均匀。采用数值模拟的方法，研究了V形导流伞夹角的角度和导流伞的位置对球罐内部流场和壁面温度的影响。结果表明，在距下人孔1/3球罐直径处安装夹角为120°的V形导流伞时，球罐壁面最大温差最小，球罐壁面温度最均匀。

球罐 热处理 V形导流伞 Fluent 温度场

目前国内大型球罐广泛采用内部燃烧法来消除焊接残余应力，即在球罐下人孔处插入燃烧器，对球罐进行加热，使其达到热处理工艺要求的温度范围[1]。在大型球罐内燃法热处理过程中，经常会出现球罐上部壁温明显高于下部壁温的现象，导致球罐热处理结果不满足工艺要求。行业内根据实践经验，采用在球罐内部安装V形导流伞改变球壁内部流场，达到减少球罐上下温差的目的[2]。但实际操作中，V形导流伞的夹角大小以及热处理时导流伞放置的位置各不相同，没有统一的标准。国内相关研究很少，笔者采用数值模拟方法[3]，运用计算流体力学软件Fluent，研究了5种不同夹角导流伞和3种不同安装位置对大型球罐内燃热处理内部流场和温度场的影响。

1 数值分析

以直径26.8m的10 000m3球罐为例，如图1所示在球罐直径上、下位置处分别设置直径0.45m，伸出长度0.5m的人孔，在距下人孔L处安装直径为4.46m，厚度为20mm的V形导流伞，在下人孔处，插入EK-9100燃烧器(燃料选用0号轻柴油)对球罐进行加热，最终达到对球罐热处理的目的[2]。燃烧器的结构简化成一个喷油嘴和一个空气入口，如图2所示。

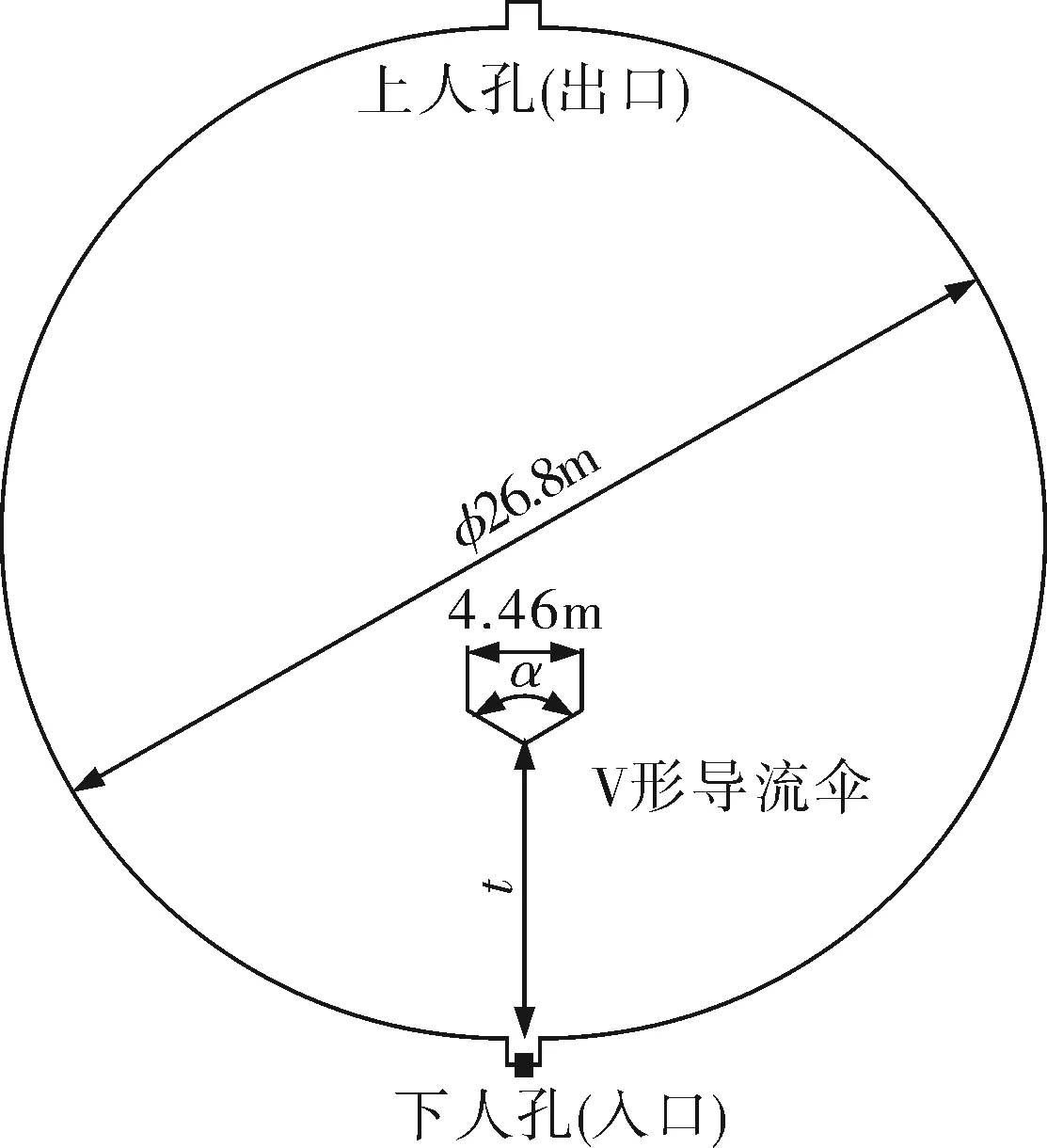
图1 10 000m3球罐热处理工艺布置示意图

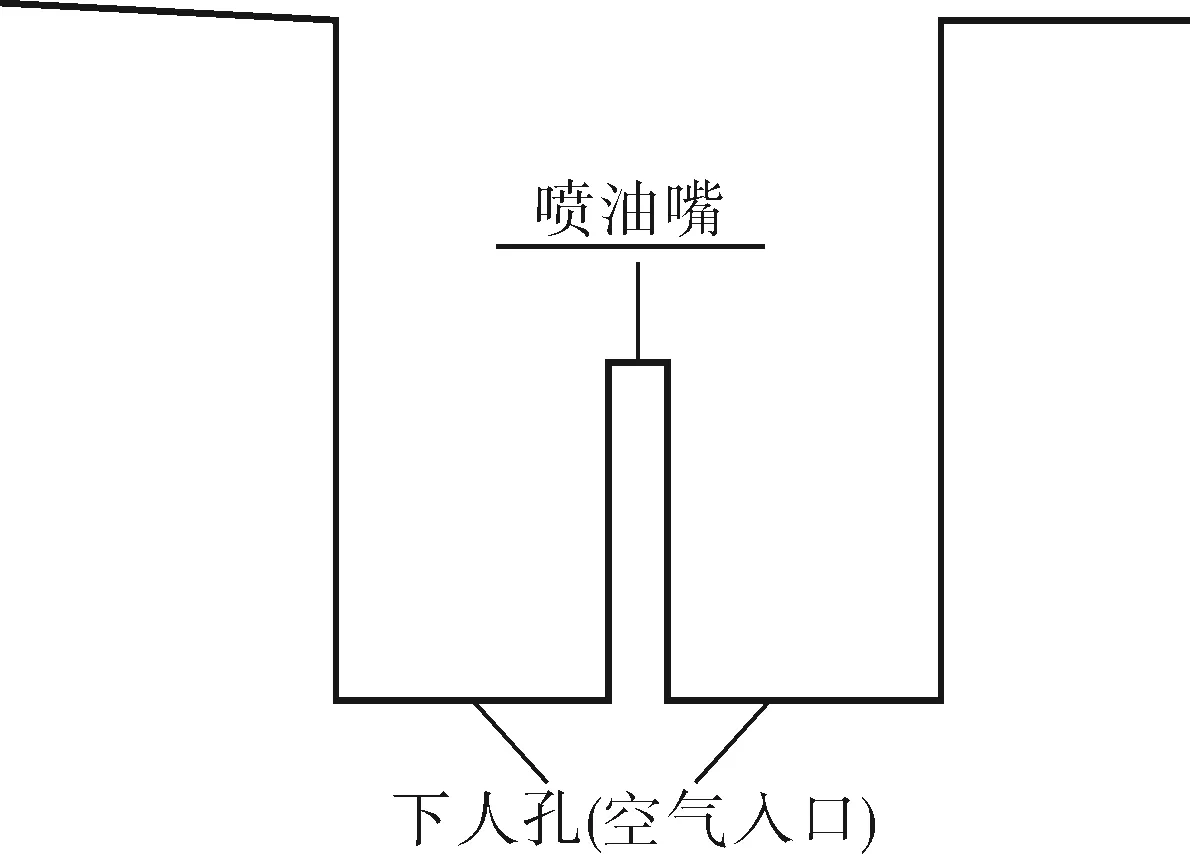
图2 燃烧器结构简化示意图

选用ANSYS Fluent数值计算软件，对球罐热处理保温阶段进行数值模拟。分析研究5种不同夹角(80、100、120、140、160°)的V 形导流伞和3种不同导流伞安装位置(距下人孔1/3D、1/2D、2/3D)时，球罐内部流场分布和壁面温度场。

2 物理数学模型

大型球罐采用内燃法热处理时，其中涉及到的物理化学过程主要包括雾化柴油的燃烧，空气的流动以及空气-球罐壁面的传热等，这些过程均满足质量守恒、动量守恒、组分守恒和能量守恒方程。在Fluent软件中选用合适的模型对其进行数值模拟[4～6]。湍流模型选用标准k-ε模型，燃料和空气从不同进口进入球罐下人孔处，燃烧模型选用非预混燃烧模型，0号柴油的射入和雾化的过程选用离散相模型。

2.1 湍流模型

球罐热处理时，被加热的热空气在球罐内部的流动采用标准k-ε模型[3～5，7～9]。标准k-ε模型是一个半经验公式，主要是基于湍流动能和扩散率。k方程是一个精确方程，ε方程是一个由经验公式导出的方程。k-ε模型假定流场完全是湍流，分子之间的粘性可以忽略。湍流能量方程和能量耗散运输方程如下：

Gk-Yk+Sk

(1)

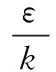
(2)

式中C1ε、C2ε、C3ε——常数，分别为1.45、1.92、1.3；

Gk——由层流速度梯度而产生的湍流动能；

Gb——由浮力产生的湍流动能；

Yk——由于在可压缩湍流中过渡的扩散产生的波动；

Sk、Sε——广义源项[4～6,10]；

σk、σε——k方程和ε方程的湍流Prandtl数为0.9。

2.2 燃烧模型

柴油和空气分别由两个入口进入，故采用非预混燃烧模型[8，9，11～14]。根据预测的混合分数分布推导出每一个组分的浓度，对非预混模型做了一定简化假设。流体的瞬时热化学状态与一个守恒量，即混合分数f相关，f可根据原子质量分数表示为：

(3)

其中，Zi表示元素i的元素质量分数。下标ox表示氧化剂流入口处的值，fuel表示燃料流入口处的值。如果所有组分的扩散系数相等，式(3)对所有元素都是相同且混合分数定义是唯一的。因此，f就是来源于燃料流的元素质量分数。在相同扩散率的假设下，组分方程可被简化为一个单一的关于混合组分f的方程。由于删去了组分方程中的反应源项，因此f是一个守恒量。平均(时间平均)混合分数方程为：

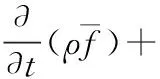
(4)

源项Sm仅指质量由液体燃料滴或反应颗粒传入气相中，Suser为任何用户定义源项[4～6,10]。

2.3 离散相模型

燃烧器燃烧过程涉及柴油雾化以及雾滴和空气之间的动量、质量、能量的传递。目前有两种数值计算方法处理多相流：欧拉-拉格朗日方法和欧拉-欧拉方法。笔者选用Fluent软件中的欧拉-拉格朗日方法的离散相模型[10，13，14]。颗粒轨迹通过颗粒作用力平衡方程来求解：

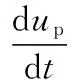
(5)

式中dp——颗粒直径；

FX——其他作用力[6,10]；

Re——相对雷诺数；

u——流体相速度；

up——颗粒速度；

μ——流体粘度；

ρ——流体密度；

ρp——颗粒密度。

3 计算方法

模型为轴对称模型，为了简化计算，建立1/2模型即可。采用四面体为主体的方式进行网格划分，共计126 640个节点，126 315个网格单元。

球罐、人孔壁和喷嘴壁的材料为金属材料，材料和介质参数见表1。

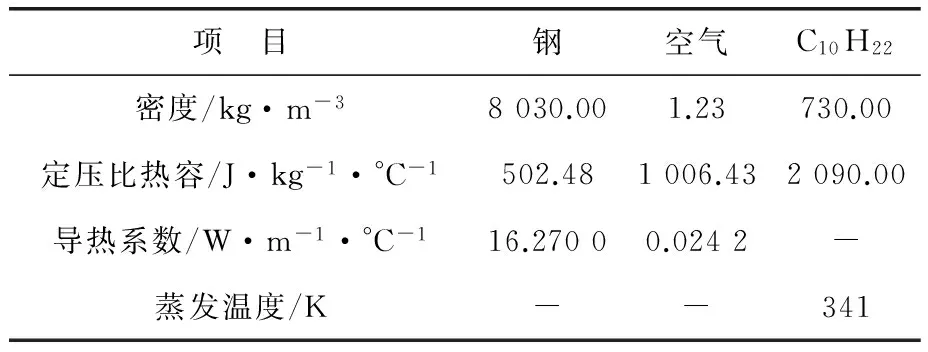
表1 材料和介质参数

笔者针对球罐热处理保温阶段进行数值计算。保温阶段可以近似看作稳态过程，稳态计算方法基于压力速度耦合求解器求解，选用SIMPLE算法，采用一阶精度迎风差分格式。先计算空气单独进入球罐的流场分布，再创建轻柴油喷射源，模拟燃烧过程，计算球罐内部的温度场分布。

下人孔空气入口边界条件：速度边界，空气流速为12.6m/s，湍流强度为5%，湍流水力直径为0.45m，空气温度为268.15K。

上人孔为出口边界条件：载荷边界，表压为0MPa。

球罐壁面厚度为36mm，选用对流传热方式，外界环境温度为268.15K，对流传热系数为0.05W/(m2K)。

喷油嘴为离散相入口，轻柴油蒸发温度341K，耗油量设为42g/s，根据elco燃烧器工作手册，工作压力为3MPa。

4 计算结果及分析

4.1 导流伞安装位置的影响

分别对导流伞安装在距下人孔1/3D、1/2D、2/3D处时的球罐热处理保温阶段进行数值模拟，如图3所示。球罐内部流场如图4所示。球罐的最高壁温、最低壁温和最大温差见表2。

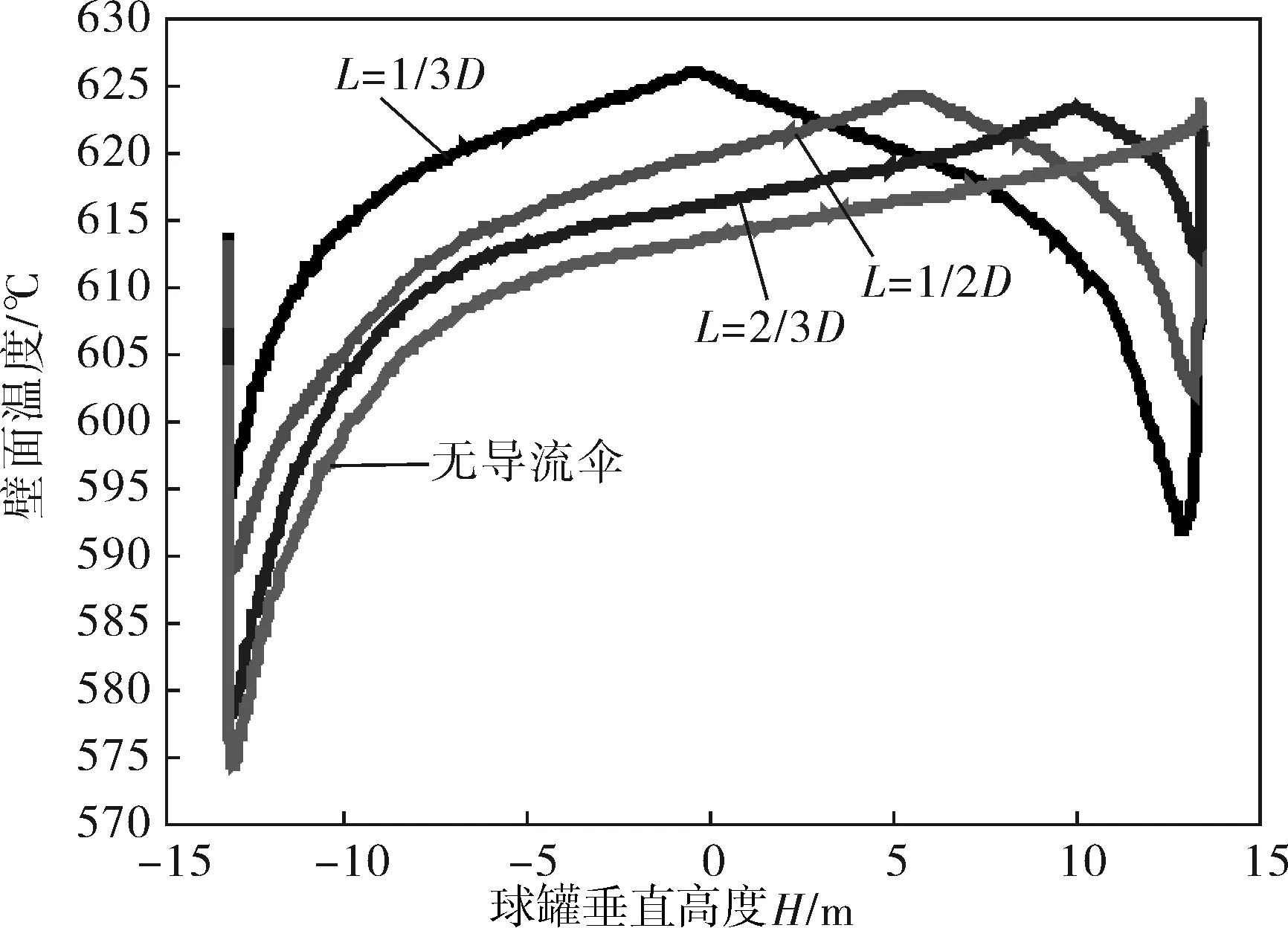
图3 球罐壁温曲线

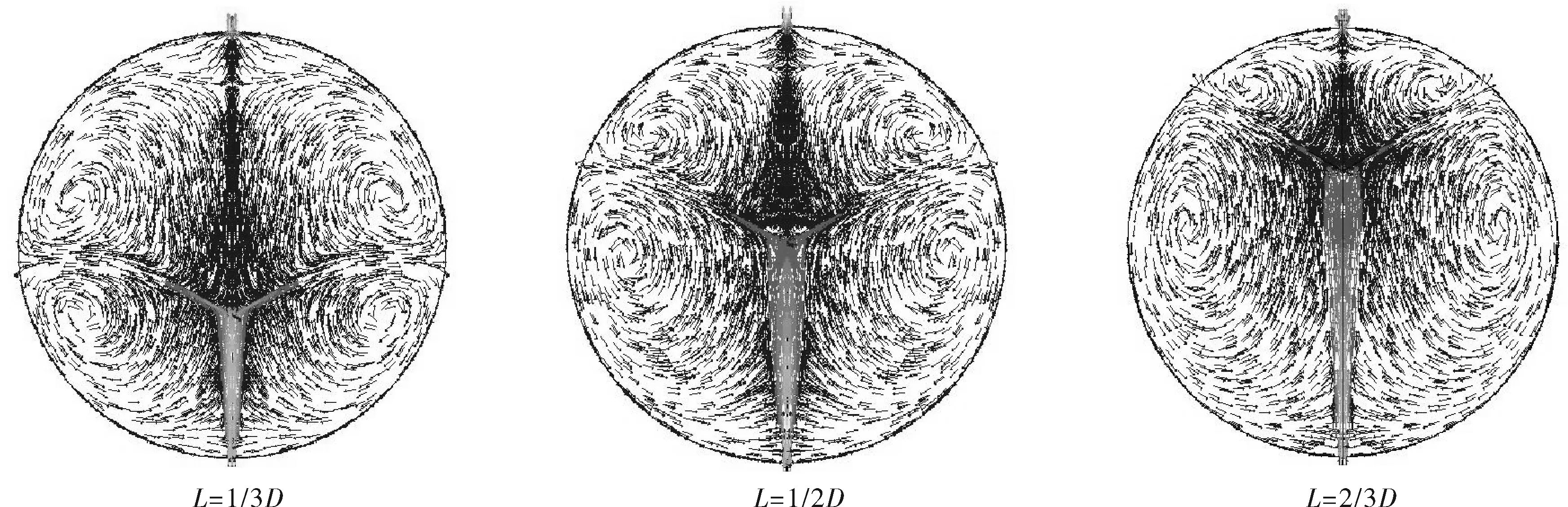
图4 球罐内部流场

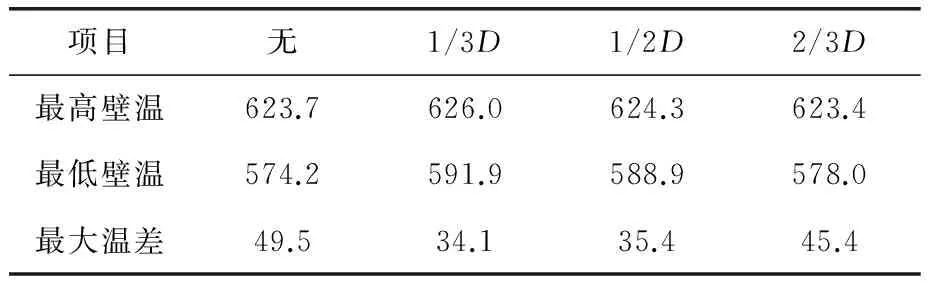
表2 导流伞不同安装位置壁温 ℃

从图3和表2可知，加入V形导流伞后，球罐壁面温度最大温差减小；导流伞安装位置L=1/3D时，球罐壁面温度最大温差最小。由图4可见，加入V形导流伞后，球罐内部流场分布产生了变化，从一侧一个漩涡变为两个，当L=1/3D时，漩涡的分界线最接近赤道。结合图3、4可以看出，球罐壁面温度的最高点在漩涡分界线附近。

4.2 V形导流伞夹角角度的影响

分别对放置在距人孔1/3D处的5种不同夹角的导流伞进行数值模拟，如图5所示。球罐的最高壁温、最低壁温和最大温差见表3，球罐内部流场如图6所示。从图5和表3可知，导流伞夹角α=120°时，球罐壁面温度最大温差最小。从图6中可以看出，导流伞夹角α=120°时，漩涡的分界线最接近赤道。结合图5、6可以看出，球罐壁面温度的最高点在漩涡分界线附近。

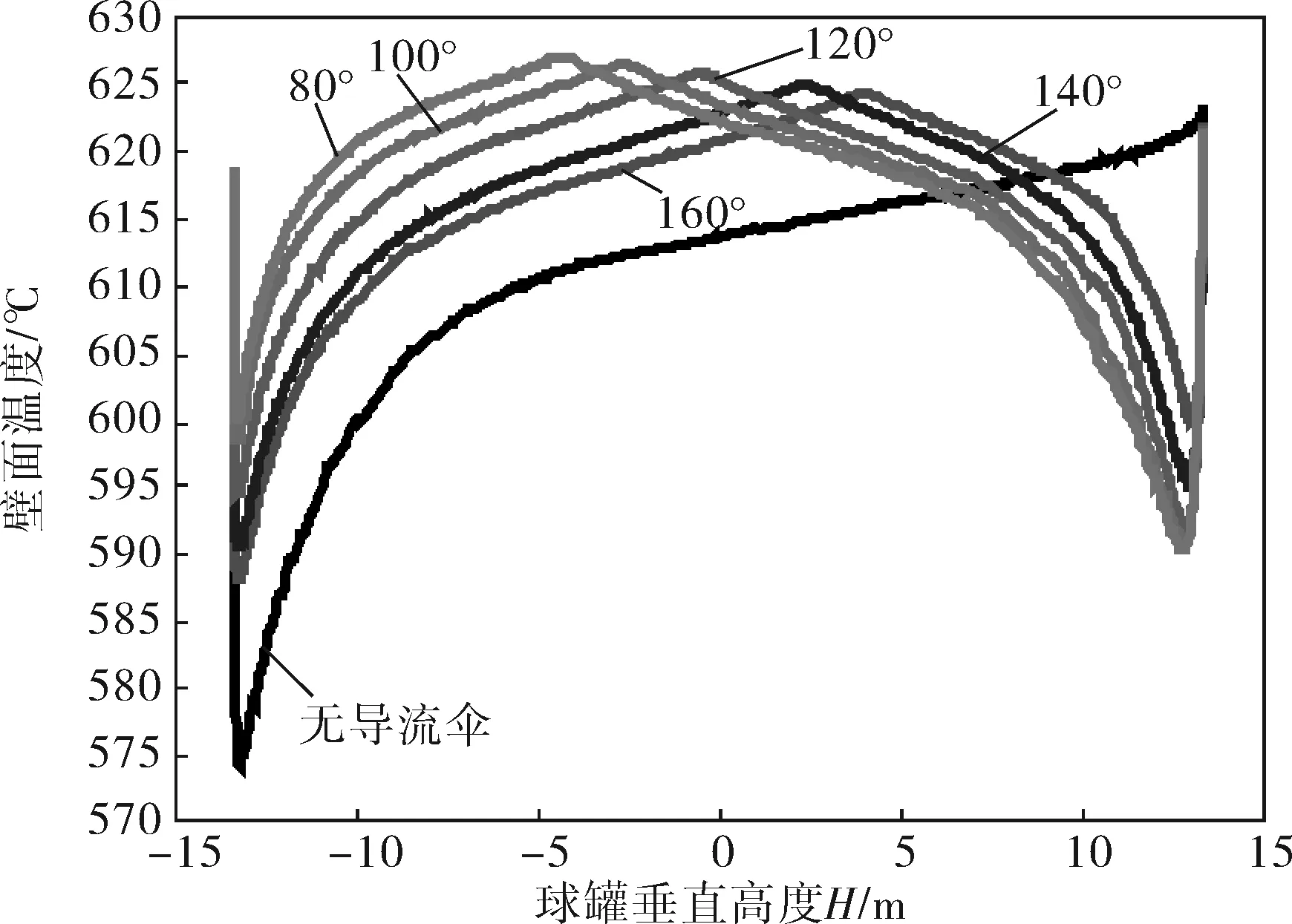
图5 球罐壁温曲线

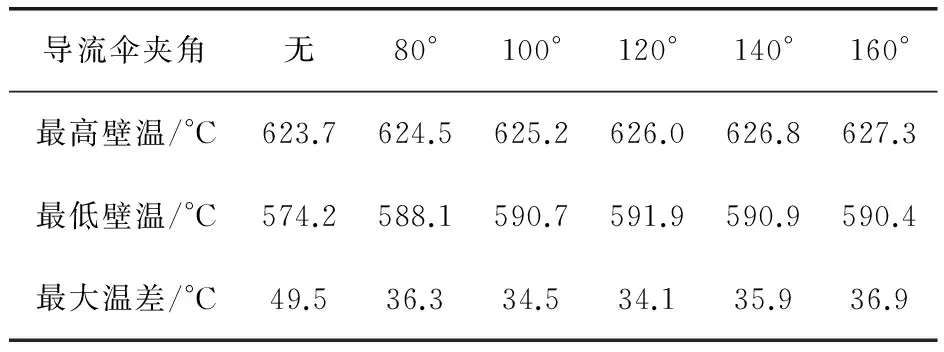
导流伞夹角无80°100°120°140°160°最高壁温/°C623.7624.5625.2626.0626.8627.3最低壁温/°C574.2588.1590.7591.9590.9590.4最大温差/°C49.536.334.534.135.936.9

5 结论

5.1大型球罐内燃法热处理时，加入V形导流伞可以改变球罐内部流场，减少球罐壁面温度最大温差。球罐壁温的最高点在漩涡分界线附近，壁面温度的最低点在球罐上下与人孔相接处。

5.2大型球罐内燃法热处理时，V形导流伞安装的最佳位置是在距下人孔1/3球罐直径处，V形导流伞的最佳夹角角度为120°。这时球罐壁面最大温差最小，球罐温度最均匀，与工程应用的实际状况基本相符。

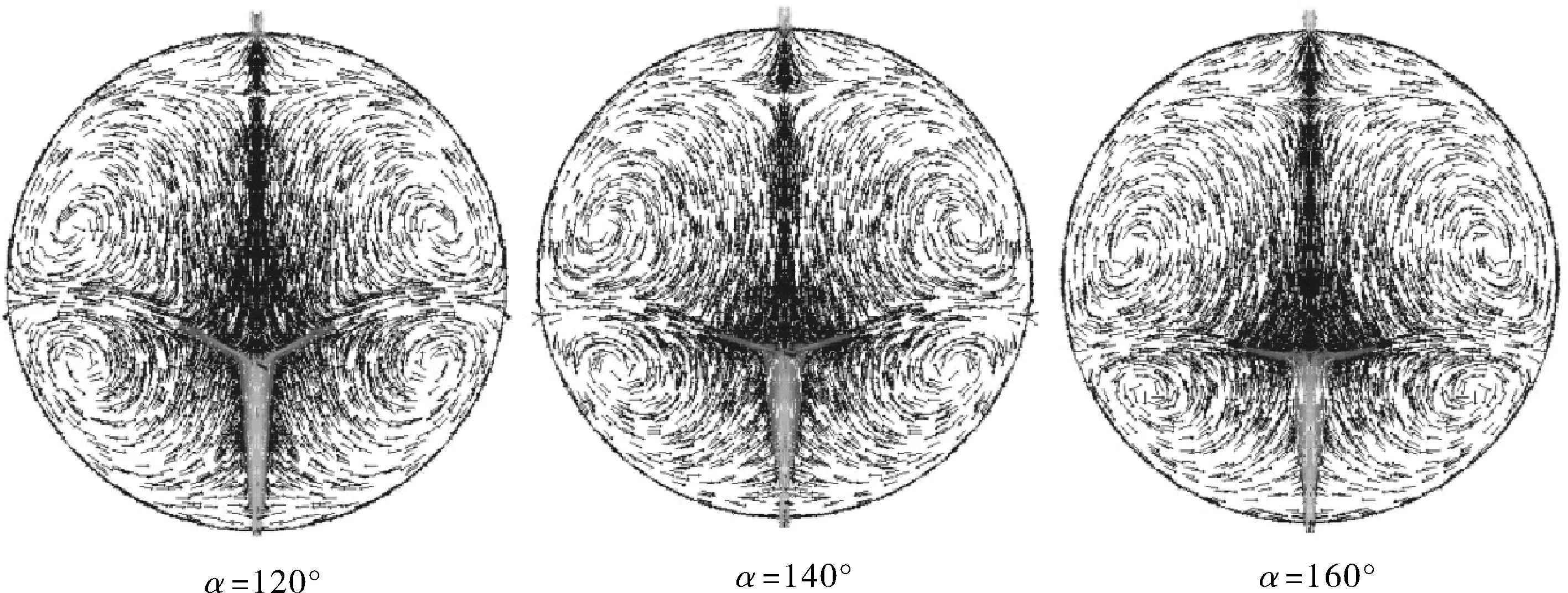
图6 球罐内部流场

[1] 傅家仁.大型球罐整体热处理方法[P].中国：1178249A，1998.

[2] 莫乾赐,鞠成伟,黄健,等.浅谈球罐焊后整体热处理[J].装备制造技术,2007，(7): 51～54.

[3] 魏强,杨文通,刘志峰.基于CFX的燃油燃气锅炉炉膛内燃烧传热的数值模拟[J].微计算机信息, 2006,22(25): 232～234.

[4] 唐家鹏.Fluent14.0超级学习手册[M].北京:人民邮电出报社,2013.

[5] 韩占忠,王敬,兰小平.Fluent流体工程仿真计算实力与应用[M]．北京：北京理工大学出版社，2004．

[6] 温正,石良辰,任毅如.流体计算应用教程[M].北京:清华大学出版社,2009.

[7] 李华莹,刘建敏,郭猛超.高原环境柴油机喷嘴内部流场与缸内温度场的三维数值模拟[J].车用发动机,2012，(5): 56～60.

[8] 艾志久,蒋静,吴昌,等.炉内燃烧场数值模拟研究[J].西南石油大学学报，2011,33(3): 165～168.

[9] 郭得锋.数值模拟在燃烧研究中的应用[J].内蒙古科技与经济,2006,8(4): 66～68.

[10] 潘国瑜.燃油燃气燃烧器燃烧与吹扫过程的试验研究及数值模拟[D].太原：太原理工大学，2011.

[11] 贾玉莲,王凤英.油罐喷射火燃烧模拟[J].工业安全与环保,2011, 37(2): 44～46.

[12] 张城伟,周长茂,王海波,等.圆筒式加热炉内辐射室燃烧数值模拟与分析[J].石油化工设备,2010, 39(5): 37～40.

[13] 李海燕,党建军,许存娥.旋转燃烧室雾化燃烧过程的数值模拟[J].火力与指挥控制,2008, 33(11): 155～161.

[14] 李海燕,冯瑞成,芮执元,等.基于数值模拟的旋转燃烧室的性能分析[J].兰州理工大学学报,2008,34(5): 64～67.

EffectofV-typeDiversionUmbrellaonHeatTreatmentTemperatureFieldinLargeSphericalTank

JI Fang1, DENG Gui-de2, LIANG Hai-feng1, DUAN Zi-hua1

(1.TaiyuanUniversityofTechnology,Taiyuan030024,China;2.ChinaSpecialEquipmentInspectionInstitute,Beijing100010,China)

In order to reduce the difference between high and low wall temperatures of the spherical tank when having the internal combustion heat treatment applied there, a V-type diversion umbrella was adopted in the spherical tank to change its internal flow field distribution so that spherical tank’s wall can be heated more evenly by hot air. Numerical simulation based on Fluent software was carried out to investigate the V-diversion umbrella’s effect on both internal flow field and wall temperatures of this spherical tank. The results show that installing V-type diversion umbrella at an included angle of 120°at the site 1/3 of the diameter to spherical tank’s bottom manhole can make tank wall’s temperature difference minimum and the wall temperature most uniform.

spherical tank, heat treatment, V-type diversion umbrella, Fluent, temperature field

TQ054

A

0254-6094(2016)01-0059-05

*国家公益性行业(质检)科研专项资助项目(201410028)。

**吉 方，男，1990年12月生，硕士研究生。山西省太原市，030024。

2015-03-12，

2015-04-13)