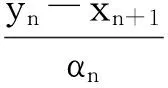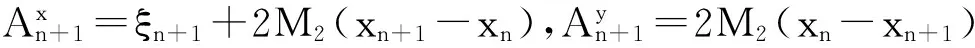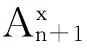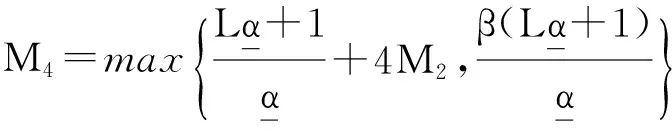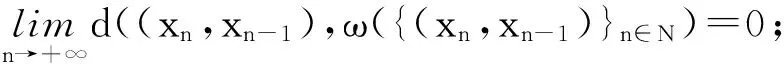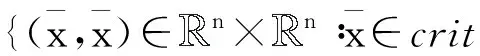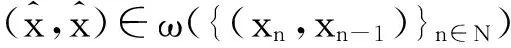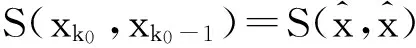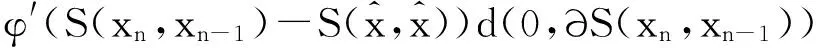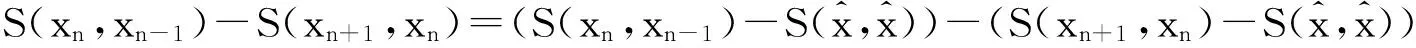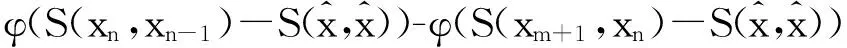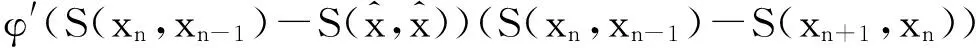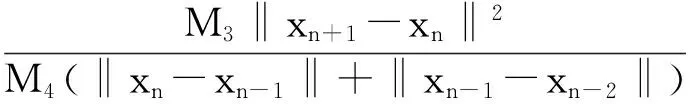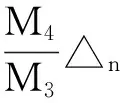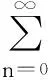非凸优化问题的惯性邻近梯度算法

刘 倩，张 征

( 西华师范大学 数学与信息学院，四川 南充 637009 )



非凸优化问题的惯性邻近梯度算法

刘 倩，张 征

( 西华师范大学 数学与信息学院，四川 南充 637009 )

研究了惯性邻近梯度法求解极小化一个非光滑函数与一个光滑函数之和的优化问题。通过假定目标函数满足KL不等式,证明了该算法的收敛性。

惯性邻近梯度法；非凸优化；KL不等式

0 引 言

本文中,我们考虑如下优化问题:

(1)

近年来,问题(1)受到了极大的关注。邻近梯度法是求解问题(1)的经典方法。2015年,PeterOchs等人在文献[1]中提出了求解问题(1)的如下惯性邻近梯度法:

xn+1=proxαnf(xn-αn▽g(xn)+βn(xn-xn-1)。

(2)

由于g为非凸函数,通过假定目标函数满足KL不等式(定义3), 他们证明了算法的收敛性。若目标函数f,g都为凸函数,通过借助Nesterov加速梯度方法的思想,Lorenz和Pock在文献[2]中提出了如下惯性邻近梯度法,

(3)

在一定的假设下,文献[2]中证明了算法(3)的收敛性。若假定为光滑函数(不一定凸),则算法(3)为

(4)

本文的目的是通过假定g为光滑函数, 借助文献[1]中证明算法(2)的思想来研究算法(4)的收敛性。值得注意的是,由文献[2]知,算法(4)比算法(2)数值效果好。这也是促使我们研究算法(4)的动机。

1 预备知识

在本节中, 我们给出一些概念和预备知识。

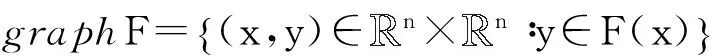
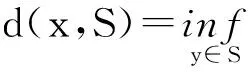
(ⅲ)h在x∈domh处的极限次微分,记作∂h(x),定义为

注1 由定义1知,

0∈∂h(x)。

(5)

(ⅲ)若h为凸函数,则∂h(x)退化为凸分析中经典的次微分定义。

注2 满足(5)的点x称为h的稳定点。h的所有稳定点集合记为crit(h)。

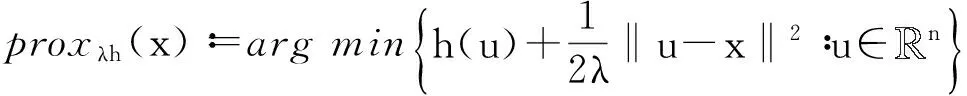
(ⅰ)φ(0)=0 ;(ⅱ)φ在(0,η)上连续可微且在0处连续;(ⅲ)φ′(s)>0,∀x∈(0,η);

(ⅳ) 对任意的x∈U∩[h(x*)

φ′(h(x)-h(x*))d(0,∂h(x))≥1。

注3 记Φη为满足(i),(ii),(iii)的函数集合。若h在dom∂h的每一点满足KL性质,则称h为KL函数。

有

引理4[8]设{ak}k∈N和{bk}k∈N为实数数列满足bk≥0,∀k∈N,{ak}k∈N下有界且ak+1+bk≤ak,对任意的k∈N。则{ak}k∈N单调递减且收敛,∑k∈Nbk<+∞。

3 收敛性分析

为方便起见, 我们将算法1.4重述于下。

其中,

(6)

惯性邻近梯度算法:

(7)

引理5 设序列{xn}n∈N由算法1.4迭代产生,则有

(f+g)(xn+1)+M1‖xn+1-xn‖2≤(f+g)(xn)+M2‖xn-xn-1‖2,∀n≥1。

(8)

其中,

证明 由(7)的第二式得

(9)

因为f为凸函数,则有

(10)

在(10)式中令得x=xn,

(11)

由引理2知,

(12)

将(11)与(12)相加可得,

(f+g)(xn)≥(f+g)(xn+1)+〈▽g(xn)-▽g(yn),xn-xn+1〉+

(13)

由于yn-xn+1=xn-xn+1+βn(xn-xn-1),则有

〈yn-xn+1,xn-xn+1〉=‖xn-xn+1‖2+βn〈xn-xn-1,xn-xn+1〉。

(14)

根据Cauchy-Schwarz不等式有,

(15)

且

(16)

又因为▽g为Lipschitz连续且yn=xn+βn(xn-xn-1),则

‖▽g(xn)-▽g(yn)‖≤L‖xn-yn‖=Lβn‖xn-xn-1‖。

(17)

将(14)-(17)代入(13)得

即证。

引理6 设序列{xn}n∈N由算法1.4迭代产生, 则有

ξn+1∈∂(f+g)(xn+1)，

证明 由(9)及注1(ⅳ)知,ξn+1∈∂(f+g)(xn+1) 。 因此,

其中,第二个不等式是根据▽g的Lipschitz连续性,第三个不等式是根据(7)的第一式。即证。

引理7 设序列{xn}n∈N由算法1.4迭代产生。则

(ⅱ)数列{(f+h)(xn)+M2‖xn-xn-1‖2}n∈N单调递减且收敛;

(ⅲ)数列{(f+g)(xn)}n∈N收敛。

证明 对任意的n≥1,记αn=(f+g)(xn)+M2‖xn-xn-1‖2,bn=(M1-M2)‖xn+1-xn‖2。由引理3.1知,

an+1+bn=(f+g)(xn+1)+M1‖xn+1-xn‖2≤(f+g)(xn)+M1‖xn-xn-1‖2=an。

根据引理4, 可知引理7的结论成立。即证。

引理8 设序列{xn}n∈N由算法1.4迭代产生。假定f+g满足强制性条件,即

则存在{xn}n∈N的子序列收敛到f+g的稳定点。事实上,{xn}n∈N的每一聚点都为f+g的稳定点。

证明 由于f+g为正常下半连续凸函数且满足强制性条件,则有f+g下有界。根据引理5有,

(f+g)(xn)≤(f+g)(xn)+M2‖xn-xn-1‖2≤(f+g)(x1)+M2‖x1-x0‖2,∀n≥1。

ξnk-▽g(xnk)∈∂f(xnk)

(18)

引理9 设序列{xn}n∈N由算法1.4迭代产生。 考虑函数

则存在M3,M4>0使得下述结论成立:

(ⅰ)S(xn+1,xn)+M3‖xn+1-xn‖2≤S(xn,xn-1);

(ⅱ)d(0,∂S(xn+1,xn))≤M4(‖xn+1-xn‖+‖xn-xn-1‖)。

证明 (i)令M3=M1-M2,由引理5及注4知, 结论成立。

(ⅱ) 因为

∂xS(x,y)=∂(f+g)(x)+2M2(x-y),∂yS(x,y)=2M2(y-x)。

(19)

则,vn+1∈∂S(xn+1,xn)。更多地,

≤‖ξn+1‖+4M2‖xn+1-xn‖

≤M4(‖xn+1-xn‖+‖xn-xn-1‖)

引理10 设序列{xn}n∈N由算法1.4迭代产生。 假定f+g满足强制性条件。 考虑函数

则下述结论成立:

(iii)S在ω({(xn,xn-1)}n∈N)上有限且为常值。

证明 (i)由定义易知该结论成立。

所以,S在ω({(xn,xn-1)}n∈N)上有限且为常值。即证。

接下来, 我们证明本文的主要结论。

定理1 设序列{xn}n∈N由算法1.4迭代产生。假定f+g满足强制性条件且函数

由于Ω为紧集且S在Ω上为常数, 由引理1知,当n>n0时有,

(20)

(21)

由引理9(i)知,

M3‖xn+1-xn‖2≤S(xn,xn-1)-S(xn+1,xn)。

(22)

将(20)和(22)代入(21), 由引理9(ii)可得

上式可等价地写为,

由Cauchy-Schwarz不等式，有

由于φ≥0,则对任意的n>n0,有

[1] OCHS P,CHEN Y J,BROX T,et al.IPiano: inertial proximal algorithm for nonconvex optimization[J].SIAM J.Imaging Sci.,2015,7:1388-1419.

[2] LORENZ D A,POCK T.An inertial forward-backward algorithm for monotone inclusions[J].J Math Imaging Vis.51:311-325.DOI 10.1007/s10851-014-0523-2.

[3] ROCKAFELLAR R T,WETS R J B.Variational analysis[M].Berlin:Springer,1998.

[4] ATTOUCH H,BOLTE J,REDONT P,et.al.Proximal alternating minimization and projection methods for nonconvex problems:an approach based on the Kurdyka-Lojasiewicz inequality[J].Mathematics of Operations Research,2010,35(2):438-457.

[5] ATTOUCH H,BOLTE J,SVAITER B F.Convergence of descent methods for semi-algebraic and tame problems:proximal algorithms,forward-backward splitting,and regularized Gauss-Seidel methods[J].Mathematical Programming,2013,137(1):91-129.

[6] NESTEROY Y.Introductory Lectures on Convex Optimization:A Basic Course[M].Boston:Kluwer Academic Publishers,2004.

[7] BOT R I,CSETNET E R.An inertial Tseng’s type proximal algorithm for nonsmooth and nonconvex optimization problem[J/OL].(2015-03-31)[2015-5-25].http://link.springer.com/article/10.1007/s10957-015-0730-z DOI:10.1007/s10957-015-0730-z.

[8] BAUSCHKE H H,COMBETTES P L.Convex analysis and monotone operator theory in Hilbert space[M].New York:Springer,2011.

Inertial Proximal Gradient Method for Nonconvex Optimization Problem

LIU Qian,ZHANG Zheng

(College of Mathematics and Information,China West Normal University,Nanchong Sichuan 637009,China)

In this paper,we investigate the inertial proximal gradient method for minimizing the sum of a nonsmooth convex function with a smooth one.By assuming the objective functions satisfy the KL inequality,we illustrate the convergence of the algorithm.

Inertial proximal gradient method;Nonconvex optimization;KL inequality

1673-5072(2016)03-0303-06

2016-03-31 基金项目：国家自然科学基金( 11371015);教育部科学技术重点项目(211163);四川省青年科技基金(2012JQ0035) 作者简介：刘 倩(1989—),女,新疆阿勒泰人,硕士研究生,主要从事优化理论研究。 通讯作者：张 征(1974—)，女，四川南充人，副教授，主要从事优化理论研究。E-mail: hi_zhangzheng@126.com

O177.91

A

10.16246/j.issn.1673-5072.2016.03.013