一种新的癫痫脑电融合特征提取方法
2016-12-24李艳艳杨陈军野梅娜
李艳艳,杨陈军,野梅娜,张 瑞
(西北大学 医学大数据研究中心, 陕西 西安 710127)
·数理科学·脑电数据分析专题研究·
一种新的癫痫脑电融合特征提取方法
李艳艳,杨陈军,野梅娜,张 瑞
(西北大学 医学大数据研究中心, 陕西 西安 710127)
癫痫是一种常见的大脑神经紊乱疾病,癫痫性发作主要由大脑中反常的神经元的超同步放电引起。为了更好地完成癫痫性发作的自动检测,文中提出了一种新的癫痫脑电融合特征提取方法。一方面,在基于Hjorth参数的振幅移动性与振幅复杂度的基础上,结合Hilbert变化提出了一种新的频率移动性与频率复杂度,然后将他们合成定义为改进的Hjorth参数特征;另一方面,结合二阶差分提出了一种改进的二阶差分样本熵。最后将改进的Hjorth参数特征与二阶差分样本熵一起作为融合特征放入超限学习机(ELM)中进行分类。数值实验结果表明,文中所提出的融合特征与ELM结合的癫痫性发作的自动检测方法与已有方法相比,检测性能有了很大提高,准确率可达到97.42%。
癫痫脑电;Hjorth参数;差分;样本熵;超限学习机(ELM)
癫痫是一种常见的大脑神经紊乱疾病。癫痫性发作主要由大脑中反常的神经元的超同步放电引起,其特点是突发性和反复性,对患者的生理和心理都造成巨大伤害,严重危害人们的正常生活,患者的过早死亡率可能是正常人的2~3倍。因此,关于癫痫的有效诊断和治疗具有十分重要的临床意义和社会意义[1-2]。
脑电图(electroencephalogram,EEG)是大脑神经细胞电活动在大脑皮层或头皮表面的总体反映,是研究癫痫的重要工具[3]。目前,医生分析癫痫患者的脑电图主要依靠视觉检查和经验判断来完成,但这样的方法存在一定的局限性[4]。首先,人工检测长时脑电是一件耗时耗力的工作,检测效率低;其次,人工检测会存在误差,对于同一段脑电不同的医生可能会有不同的结论,甚至同一个医生在不同时间下的结论也可能不同,缺乏一定的客观性。基于以上问题,癫痫性发作的自动检测成为近年来的研究热点问题。
20世纪60年代以来,癫痫性发作的自动检测技术有了很大提高,并提出了多种自动检测的方法。这些方法主要可以归类为时域分析、频域分析、时频分析、非线性方法等[5-6]。时域分析直接从脑电的时间域中对信号进行分析,具有直观性的优点。常用的方法有信号的方差、均值、峰值检测、过零截点分析等[7];频域分析是脑电分析和临床应用中一种主要分析方法,可以反映脑电信号的能量状态等情况。常用的有功率谱估计谱熵[8]等;单一的时域或频域分析容易丢失脑电信号中与病变相关的瞬态信息,所以近年来,时频分析在脑电分析中得到了较大的发展。常见的时频分析方法有小波分析[9]、二次时频分布[10]等。由于脑电信号是一种非线性信号,近年来采用非线性方法提取癫痫脑电特征也成为一个研究方向。常见的非线性分析方法有最大李雅普诺夫指数(Lyapunov指数)[5]、分形维数[11]、复杂度分析[12]、Hurst指数[13]、熵算法[14]等。
本文首先提出了一种新的癫痫脑电融合特征提取方法。一方面,在基于振幅的Hjorth参数移动性与复杂度的基础上,本文结合Hilbert变化提出了一种基于频率的Hjorth参数移动性与复杂度,然后将他们合成定义为改进的Hjorth参数特征;另一方面,本文结合二阶差分提出了一种改进的二阶差分样本熵。在上述工作的基础上,本文将改进的Hjorth参数特征与二阶差分样本熵进行特征融合,提出一种新的融合脑电特征提取方法。其次,结合超限学习机(extreme learning machine, ELM)完成癫痫性发作的自动检测。
1 新的融合特征提取方法
本小节将介绍基于改进Hjorth参数特征和二阶差分样本熵的一种融合特征提取方法。
1.1 差分运算
差分运算反映了离散量之间的一种变化,主要应用在误差修正和数据平稳处理上。与高阶导数类似,也有高阶差分的概念。二阶及二阶以上的差分称为高阶差分。这里主要介绍一阶差分和二阶差分。
给定一个信号X={x(1),x(2),…,x(T)},其中T表示每个信号的长度。则X的一阶差分信号为
X′={x′(1),x′(2),…,x′(T-1)},
x′(t)=x(t+1)-x(t), t=1,2,…,T-1。
(1)
类似地,X的二阶差分信号为
X″={x″(1),x″(2),…,x″(T-2)},
x″(t)=x(t+2)-2x(t+1)+x(t), t=1,2,…,T-2。
(2)
1.2 改进的Hjorth参数特征
1.2.1 基于振幅的Hjorth参数特征 Hjorth参数是由Bo Hjorth在1970年首次提出的,广泛应用于脑电信号分析[15-18]。共包含3个参数,分别定义为活动性(Activity)、移动性(Mobility)和复杂度(Complexity)。本文选取移动性和复杂性作为特征提取的参数指标。
对于给定信号X={x(1),x(2),…,x(T)},首先计算X的标准差为
(3)
其次,根据公式(1)和(2)计算信号X的一阶差分方程和二阶差分方程,并据此分别计算一阶差分标准差
(4)
及二阶差分标准差
(5)
在此基础上,脑电信号的移动性(Mobility)定义为一阶差分标准差与标准差的比值。记作
(6)
脑电信号的复杂度(Complexity)则进一步定义为
(7)
Hjorth参数计算简单,便于实现,因此广泛用于睡眠脑电、癫痫检测等的研究中。
1.2.2 基于频率的Hjorth参数特征 Hilbert变换[19-20]广泛应用于信号处理中,可以解决信号瞬时特征的提取问题,包含瞬时包络、瞬时相位及瞬时频率。
给定信号X={x(1),x(2),…,x(T)},对其实施Hilbert变换,可表示为
(8)
其中H表示Hilbert变换,*表示卷积。于是,信号x(t)的瞬时频率ω(t)可定义如下
(9)

(10)

(11)
1.3 二阶差分样本熵算法
样本熵(sample entropy,SampEn)是由Richman[21]提出的一种时间序列复杂性的度量方法。相对于近似熵而言,样本熵在计算中不包括自身数据的比较,不依赖于数据长度,具有更好的一致性和更高的准确度,并且对于丢失数据不敏感,是对近似熵算法的改进。样本熵值越大,表示序列越复杂。由于脑电信号在癫痫发作时的复杂度降低,因此可以采用样本熵的值作为特征来检测脑电信号发作与否。
本小节介绍一种改进的样本熵定义。首先按照公式(2)计算脑电信号的二阶差分信号,然后计算二阶差分信号的样本熵。我们称之为二阶差分样本熵,具体算法总结如下。
二阶差分样本熵算法 给定脑电信号X={x(1),x(2),…,x(T)},其中T表示信号的长度。
步骤1 运用公式(2)计算信号X的二阶差方信号,记作
Y={y(1),y(2),…,y(N)}, N=T-2
其中y(i)=x″(i)。
步骤2 按顺序组成一组m维矢量
ym(i)=[y(i),y(i+1),…,y(i+m-1)],
1≤i≤N-m;
(12)
步骤3 定义矢量Ym(i)与Ym(j)之间的距离为两者对应元素中差值最大的一个,即
d[Ym(j),Ym(j)]=
max[|y(i+k)-y(j+k)|];
(13)
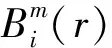

(14)
步骤5 求其对所有的i的平均值,用Bm(r)表示,即
(15)
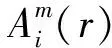
步骤7 定义样本熵为
(16)
当N为有限值时,上式可以表示成
(17)
1.4 一种新的融合特征
给定一组脑电信号Χ={X1,X2,…,XΓ},其中Xi={xi(1),xi(2),…,xi(T)}表示第i个脑电信号,Γ表示脑电信号的总数,T表示每个信号的长度。


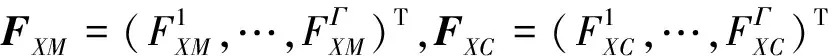

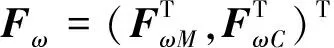

步骤3 将改进的Hjorth参数特征表示为
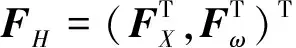
步骤4 根据二阶差分样本熵算法计算脑电信号Xi的二阶差分样本熵,记为

步骤5 将改进的Hjorth参数特征与二阶差分样本熵放在一起作为新的融合特征
F=(FHT,FST)T。
2 超限学习机(ELM)
超限学习机(ELM)是2006年Huang等人提出的一种新的快速学习算法[22],它克服了传统学习算法学习速度慢,并且容易陷入局部极大或极小的问题,现已被广泛应用于分类和回归问题中。
oj, j=1,…,N。
(18)
其中G(ai,bi,x)为隐层输出函数,oj为网络输出,(ai,bi)∈Rn×R为连接第i个隐单元的权重向量和阈值,βi=[βi1,…,βim]T是连接第i个隐层结点和输出结点的权重向量,ai·xj表示ai与xj的內积。
若网络的实际输出oj等于期望输出tj,即
(19)
上述N个等式可等价地表示为如下矩阵形式:
Hβ=T。
(20)
其中
H(a1,..,aL,b1,..,bL,x1,..,xN)=
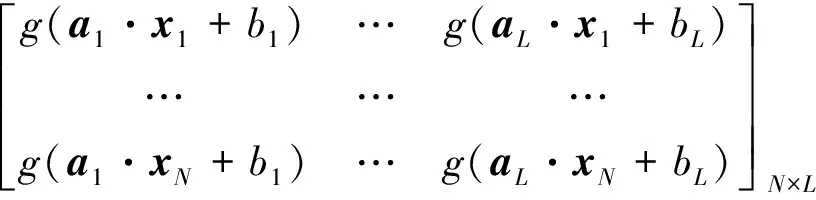
(21)
(22)
H称为单隐层神经网络的隐层输出矩阵,其第i行表示输入xi关于每个隐结点的输出,第j列表示输入x1,…,xN分别对应于第j个隐结点的输出。在ELM运算过程中,ai和bi由计算机随机给出,则问题转化为求解β。
综上所述,ELM的算法如下:
给定训练数据集,激活函数g(x),隐层结点个数L。
第一步:随机选取输入权重ωi,阀值bi,i=1,2,…,L;
第二步:计算隐层输出矩阵H;
第三步:计算输出权重β=H†T,其中H†为H的广义逆。
3 数值实验结果及分析
3.1 脑电数据
本文所用的脑电数据都是来自于德国波恩大学癫痫研究室临床采集的癫痫脑电数据库,是目前应用比较广泛的一个公开数据库[23]。共包含5个数据集,分别来自5个健康人和癫痫患者的脑电信号,标记为Z,O,N,F和S。每个数据集包含100个片段,采样率为173.61Hz,持续时间为23.6s。
数据集Z和O是健康人清醒状态下的脑电信号,其中Z是睁眼时候信号,O是闭眼时候的信号;数据集N,F,S是癫痫病人的脑电信号,N,F数据集是发作间歇期脑电信号,N是癫痫病人颅内病灶区外的海马结构的脑电信号,F是癫痫病人颅内病灶区的脑电信号;数据集S是癫痫发作期脑电。
研究表明, 相比正常脑电与发作脑电, 发作间歇期脑电与发作期脑电的判别更为困难。因此,本文仅在两个数据集F和S上来验证所提特征提取方法在癫痫发作检测中的可行性与有效性。每个数据集各包含100个片段,每个片段数据点个数为4 097,共得到200段数据。文中所有数值实验均是在 Matlab 8.1.0中运行。

图1 数据集F,S的EEG片段Fig.1 The EEG segments in set F and set S
3.2 结果与分析
在样本熵计算过程中,样本熵的值与嵌入维数m和阈值r有关。本文在计算中选取m=2,r=0.2SD,其中SD是信号Y的标准差。
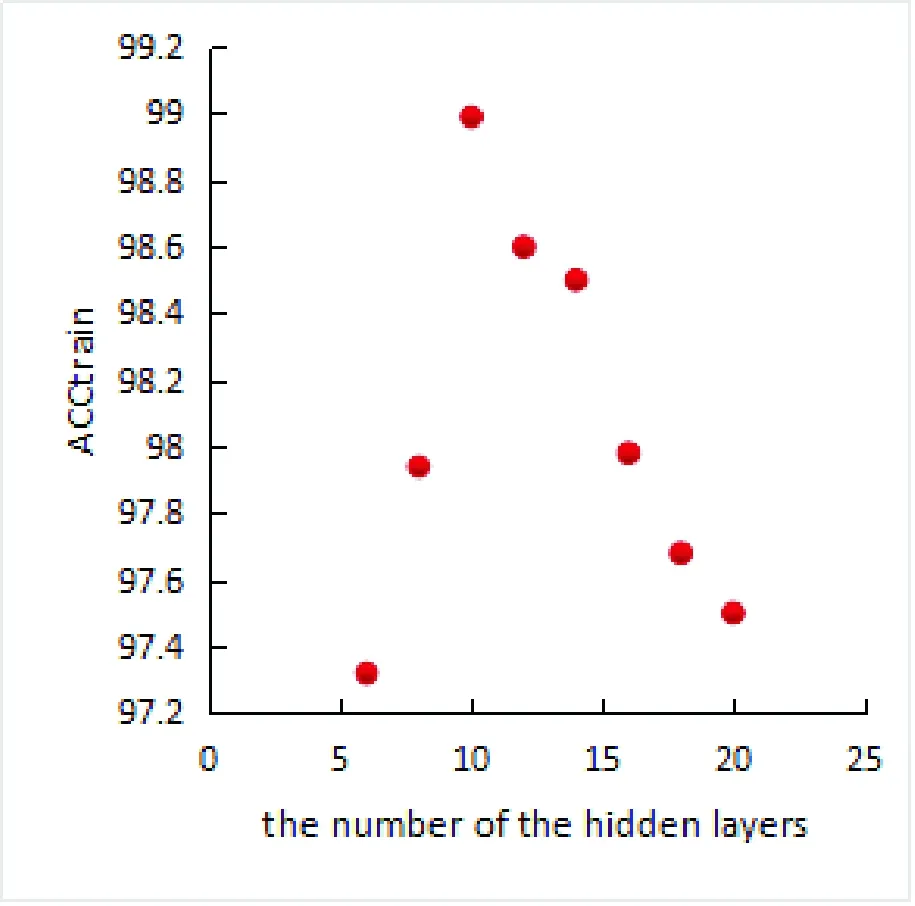
图2 ELM中不同隐节点在训练集上的准确率Fig.2 The training accuracy of ELM with different numbers of hidden nodes
在ELM中,激活函数为Sigmoid函数,隐节点个数选取为可加型节点,通过多次训练后取最佳准确率。本文中隐节点个数从6开始按步长为2增加至20,具体结果如图2所示。从图2可以看出,随着隐节点个数的增加,在隐节点个数为10时达到最大训练准确率99%,故选择隐节点个数为10。在运行过程中,所有数据被随机均分为训练集和测试集, 为了降低随机均分所导致的训练集和测试集中不同类数据点的不均衡, 本文将这种随机均分的实验执行50 次, 并以50次实验的平均结果作为最终分类性能的度量。
在SVM中,核函数选取径向基函数(radial basis function, RBF)。SVM中的正则参数C和核参数g通过十倍交叉验证的网格搜索方法(grid search method)确定。相应的效果图如图3所示,根据训练集上的平均最佳分类准确率100%,确定最佳的(C,g)为(2, 1)。

图3 SVM参数C-g等高线图Fig.3 The C-g contour plot of SVM with grid search
本文采用灵敏度Se、特异性Sp和准确率Pr作为评估算法的参考值,它们的定义分别为:
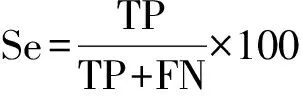
(23)

(24)
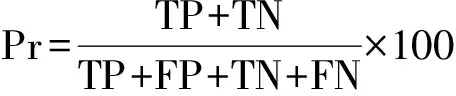
(25)
式中TP表示真阳性(true positive,TP),即实际为发作脑电,并且被正确检测为发作脑电;FP表示假阳性(false positive,FP),即实际为正常脑电,但被错误判定为发作脑电;TN表示真阴性(true negative,TN),即实际为正常脑电,且被判定为正常脑电;FN表示假阴性(false negative,FN),即实际为发作脑电,但被判定为正常脑电。
首先验证振幅移动性、振幅复杂度、频率移动性、频率复杂度以及二阶差分样本熵这5个单一特征的有效性与可行性。图4与图5分别表示上述3类特征的箱线图。由图4可见,癫痫发作间歇期脑电的振幅移动性与频率复杂度总体上低于发作期脑电的对应值;癫痫发作间歇期脑电的振幅复杂度与频率移动性总体上高于发作期脑电的对应值。由图5可见,癫痫发作期脑电的二阶差分样本熵低于发作间歇期的对应值。所有这些结果都说明,上述5种参数值均可以作为判断癫痫脑电发作与否的一个特征。

图4 间歇期脑电和发作脑电的Hjorth参数特征箱线图Fig.4 The boxplot of the Hjorth parameters corresponding to inter-ictal EEGs and ictal EEGs

图5 间歇期脑电和发作脑电的二阶样本熵箱线图Fig.5 The boxplot of the second-order differential Sample Entropy corresponding to inter-ictal EEGs and ictal EEGs
其次验证本文所提出的新的融合特征在癫痫性发作自动检测中的性能。表1展示的是3种不同特征(即改进的Hjorth参数特征、二阶差分样本熵、以及融合特征)的性能比较结果。从表1可看出,融合特征的分类性能比改进Hjorth参数特征和二阶差分样本熵都有了明显提升,其准确率可达到97.42%,敏感度达到97.25%,特异性达到97.65%。
表1 3种不同特征提取方法的性能比较
Tab.1 Performance comparison of three feature extraction methods

性能改进的Hjorth参数特征二阶差分样本熵融合特征准确率/%959888979742敏感度/%952489399825特异性/%983488589765
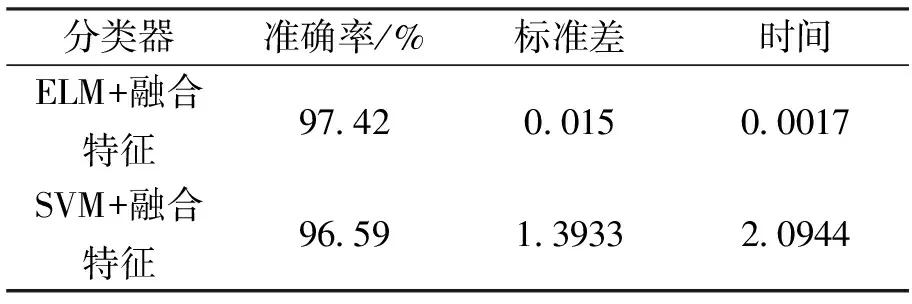
表2展示的是“融合特征+ELM”与“融合特征+SVM”两种自动检测方法所得到准确率、标准差及网络的训练时间。从表2可以看出,在分类准确率、稳定性和分类时间上,ELM的分类性能均优于SVM。
表2 ELM和SVM关于融合特征的性能比较
Tab.2 Performance comparison of the ELM and SVM with the same fusion feature
分类器准确率/%标准差时间ELM+融合特征9742001500017SVM+融合特征96591393320944
最后,本文对所提的自动检测方法(即“融合特征+ELM”)与其他已有检测方法的检测性能进行了系统的比较。为了比较的客观性,本文仅列出在相同数据集(波恩大学数据库的F和S集)上的检测结果。表3列出了本文所提方法与已有6个方法的比较,分别为近似熵+ELM(Approximate entropy+ELM);Hurst指数+ELM(Hurst exponent+ELM);去趋势波动分析+ELM(DFA+ELM);排列熵+SVM(Permutation entropy+SVM);多重排列熵+SVM(MPE+SVM);经验模态分解和去趋势+ELM(EMD and DFA+ELM)。由表3可以看出,本文所提的新的融合特征的分类性能好于其他方法,准确率有了一定程度的提升。
表3 本文所提方法与已有方法的检测性能比较
Tab.3 Perforence comparision between the proposed method and some existing methods

作者年份方法准确率/%Qiyuanetal2012Approximateentropy+ELM88Hurstexponent+ELM885DFA+ELM82Nicolaouetal2012Permutationentropy+SVM8313XiMinetal2015MPE+SVM9470LiuXiaofengetal2015EMDandDFA+ELM94.75ThispaperFusionFeature+ELM97.42
4 结 论
本文提出了一种新的癫痫脑电融合特征提取方法。一方面,在基于Hjorth参数的振幅移动性与振幅复杂度的基础上,本文结合Hilbert变化提出了一种新的频率移动性与频率复杂度,然后将他们合成定义为改进的Hjorth参数特征;另一方面,本文结合二阶差分提出了一种改进的二阶差分样本熵。在上述工作的基础上,本文将改进的Hjorth参数特征与二阶差分样本熵进行特征融合,提出一种新的融合脑电特征提取方法。其次,结合超限学习机(Extreme learning machine, ELM)完成癫痫性发作的自动检测。应用于德国伯恩大学脑电数据库上的数据集F和数据集S上,数值实验结果表明,本文所提出的融合特征具有较高的性能,能较好地完成癫痫性发作的自动检测。
[1] CORREA A G, LORENAOROSCO P D, LACIAR E. Automatic detection of epileptic seizures in long-term eeg records [J]. Computer in Biology and Medicine, 2015,57: 66-73.
[2] 刘小峰, 张翔, 王雪. 基于EEG去趋势波动分析和极限学习机的癫痫发作自动检测与分类识别[J]. 纳米技术与精密工程, 2015, 13(6): 397-403.
[3] 袁琦, 周卫东, 李淑芳等. 基于ELM和近似熵的脑电信号检测方法[J]. 仪器仪表学报, 2012, 33(3): 514-519.
[4] HUANG L Y, ZOU J, MA H J, et al. Brain functional network based on mutual information analysis of EEGs and its applcation to schizophrenia[J].Advanced Materials Research, 2013, 718-720:1440-1445.
[5] KANTZ H, SCHREIBER T. Nonlinear Time Series Analysis[M].Cambridge University Press, Cambridge, 1997.
[6] YUAN Qi, ZHOU Weidong. Epileptic EEG classification based on extreme learning meachine and nonlinear features [J].Epilepsy Research, 2011,96:29-38.
[7] GREENE B R, FAUL S, MARNANE W P, et al. A comparison of quantitative EEG features for neonatal seizure detection[J].Clinical Neurophysiology, 2008,119:1248-1261.
[8] REZEK I A, ROBERTS S J. Stochastic complexity measures for physiological signal analysis[J].IEEE Trans Biomed Eng, 1998, 45: 1186-1191.
[9] OSVALDO A,BLANCO R S,FIGLIOLA A. Wavelet entropy: a new tool for analysis of short duration brain electrical signals[J]. Journal of Neuroscience Methods,2001,105: 65-75.
[10] COHEN I. Time-frequency distributions-a review[J]. Proceedings of the IEEE, 1989, 77(7): 941-981.
[11] ACCARDO A, AFFINTO M, CAROZZI M, et al.Use of the fractal dimension for the analysis of electroencephalographic time series[J]. Biol Cybernetics, 1997, 77: 339-350.
[12] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Phys. Rev. Lett,2002, 88: 1595-1602.
[13] NURUJJAMAN M,RAMESH N,SEKAR IYENGAR A N. Comparative study of nonlinear properties of EEG signals of normal persons and epileptic patients[J]. Nonlinear Biomedical Physics,2009,3(1):6-11.
[14] ACHARYA U R, MOLINARI F. Automated diagnosis of epileptic EEG using entropies[J]. Biomedical Siganl Processing and Control, 2012,7: 401-408.
[15] BO HJORTH. EEG analysis based on time domain properties[J], Electroenceph. elin. Neurophysiology. 1970, 29:306-310.
[16] GREENE B R, FAUL S, MARNANE W P, et al. A comparison of quantitative EEG features for neonatal seizure detection[J]. Clinical Neurophysiology, 2008,119:1248-1261.
[17] PAIVINEN N, LAMMI S, GRONFORS T. Epileptic seizure detection: A nonlinear viewpoint[J].Computer Methods and Programs in Biomedicine, 2005,79: 151-159.
[18] KANG Jaehwan, CHUNG Yoongi, KIM Sungphil. Anefficient detection of epileptic seizure by differentiation and spectral analysis of electroencephalograms[J].Computers in Biology and Medicine, 2015,66(c):352-356.
[19] 刘慧婷,程家兴,张旻. 利用Hilbert变换提取信号瞬时特征的算法实现[J]. 微机发展,2003,13(6): 82-85.
[20] FU Kai, QU Jianfeng, CHAI Yi,et al. Classification of seizure based on the time-frequency image of EEG signal using HHT and SVM[J]. Biomedical Signal Processing and Control, 2014, 13: 15-22.
[21] RICHMAN J S, MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J].Am J Phisiol Heart Circ Physiol, 2000, 278: 2039-2049.
[22] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning ma chine: theory and applications[J].Neurocomputing, 2006,70: 489-501.
[23] ANDRZEJAK R G, LEHNERTZ K, MORMANN F, et al. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity:Dependence on recording region and brain state[J].Physical Review E,2001, 64(6): 061907.
(编 辑 亢小玉)
A novel fusion feature extraction method for epileptic EEG
LI Yanyan, YANG Chenjun, YE Meina, ZHANG Rui
(Medical Big Data Research Center, Northwest University, Xi′an 710127, China)
Epilepsy is one of the most common neurological disorders. It is characterized by recurrent epileptic seizures, which are caused by hypersynchronous discharges of an excessive group of cells in the brain. In this paper, a novel fusion feature extraction method is proposed for realizing the automatic seizure detection using epileptic EEGs successfully. On one hand, the frequency mobility and frequency complexity are defined. And further, combining with the Hjorth parameters, an improved Hjorth-parameters-based feature is designed. On the other hand, the second-order differential sample entropy is presented, which is based on the sample entropy and second-order differential method. Then the fusion feature, which combing the improved Hjorth-parameters-based feature and the second-order differential sample entropy, are fed into extreme learning machine (ELM) to complete the epileptic seizure detection. Experimental results show that the proposed seizure detection method achieves the detection accuracy at 97.42%, whose performance is greatly improved compared with some other existing methods.
epileptic electroencephalogram(EEG); Hjorth parameters; differential; sample entropy; extreme learning machine (ELM)
2016-03-19
国家自然科学基金资助项目(61473223);陕西省自然科学基础研究计划基金资助项目(2014JM1016)
李艳艳,女,陕西铜川人,从事癫痫脑电的特征提取研究。
张瑞,女,陕西西安人,西北大学教授,博士生导师,从事机器学习理论与算法,脑电心电数据分析等研究。
O29
A
10.16152/j.cnki.xdxbzr.2016-06-004
