基于Hopf振荡器的六足机器人步态CPG模型设计
2016-12-24任杰徐海东干苏王斌锐
任杰,徐海东,干苏,王斌锐
(中国计量学院 机电工程学院,浙江 杭州 310018)
基于Hopf振荡器的六足机器人步态CPG模型设计
任杰,徐海东,干苏,王斌锐
(中国计量学院 机电工程学院,浙江 杭州 310018)
利用中枢模式发生器实现六足机器人爬行步态是运动仿生的关键。建立机器人坐标系,基于D-H参数求解正运动学;采用Hopf振荡器设计多腿耦合模型;构建由6个CPG单元组成的环形CPG网络拓扑结构,每个CPG单元由2个耦合的Hopf振荡器组成,分别输出髋关节、踝关节运动信号;采用膝踝映射函数方法,将踝关节输出信号映射为踝关节和膝关节角度轨迹,从而降低网络中振荡器个数;通过改变耦合系数保证相邻振荡器的相位互锁,输出稳定平滑信号;搭建实物样机进行步态测试。仿真和实验表明,CPG网络相位差稳定,可实现六足机器人三角步态下的平稳行走,爬行速度约为6.45 cm/s。
中枢模式发生器;Hopf振荡器;六足机器人;运动学分析
六足机器人具有稳定的机械结构、灵活多变的行走方式,适合在复杂环境下工作,被广泛应用于灾后探测、环境勘测等工作中。大量研究表明,昆虫及其他生物的节律步态,是根据生物神经节律控制机理产生的一种自激振荡、相位互锁的运动模式,由位于生物低级神经中枢的中枢模式发生器(central pattern generator,CPG)产生的信号控制[1-2]。CPG已被广泛应用于机器鱼、机器海龟、机器果蝇等机器人控制领域[3-5]。与传统的基于模型的机器人控制方法相比,CPG不需要对机器人本体和环境进行建模,不依赖于外部反馈和高层命令而产生稳定的节律运动,可适应非结构化环境,具有运动模式多样、耦合性强、自适应性强等优点。
根据不同的应用环境,CPG模型被分为不同类型[2],如生物神经元模型、半中心模型、耦合振荡器模型等。常见的主要是半中心模型和耦合振荡器模型。半中心模型是模拟伸肌和屈肌的交替运动。根据半中心模型思想,Matsuoka对漏极积分器进行改进,加入模拟神经元适应特性的疲劳项,构成Matsuoka神经振荡器[3]。基于Matsuoka振荡器模型,Kimura等[4]在CPG中加入传感器反馈,采用2个相互抑制的屈肌和伸肌神经元构成了Kimura模型,提高了四足机器人运动的稳定性,但存在控制算法复杂,参数难调节等缺点。耦合振荡器模型由非线性振荡器组成,模型参数直接对应输出曲线的物理含义,实现幅值、频率等参数可调,便于控制。常见的有Kuramoto振荡器模型、Hopf振荡器模型、Wilson-Cowan振荡器模型等[6-7]。A. J. Ijspeert团队[8]将非线性振荡器应用在两栖蝾螈机器人上,实现了机器人游泳和步行运动。
本文仿生对象是蚂蚁。首先参考蚂蚁的腿部结构比例,进行单腿正运动学分析,设计六足机器人。其次,采用L. Righetti和A. J. Ijspeert的改进Hopf非线性振荡器构建CPG模型[9],构建环形网络拓扑结构。然后设计膝踝映射函数,减少振荡器数量,优化了CPG网络结构;通过Matlab仿真得到关节角度;最后在六足机器人上进行实物验证。
1 六足机器人的基本机构及步态
1.1 六足机器人机构
本文设计的六足仿生机器人分为躯干和肢体两部分,仿生对象为蚂蚁。肢体设计参考了非洲红火蚁的腿部结构比例,如图1所示,蚂蚁的腿部主要由基节、股节、胫节及跗节等组成。通过观察发现,蚂蚁的腿部自由度较多。为简化设计,六足机器人每条腿3个自由度,分别为髋关节、膝关节和踝关节,对应蚂蚁腿部分别是基关节、基-股关节、股-胫关节。其中,机器人的膝关节和踝关节转轴与地面平行,髋关节转轴与另外2个关节垂直,髋关节控制单腿的水平方向的横摆。
根据仿生蚂蚁腿部结构及机器人学原理,对六足机器人进行运动学建模。图2为六足机器人机构坐标系,图2(a)中c为机器人躯干质心坐标原点,定义∑c表示机器人躯干质心坐标系,zc沿垂直身体向上,xc沿身体横向方向,yc坐标轴通过右手螺旋定则确定,为躯体轴线前进方向。omi为m腿i关节中心坐标原点,用∑omi表示其关节坐标系,∑om0表示机器人腿部基坐标系。图2(b)中,m=1,2,…,6为机器人腿序号,i=1,2,3为腿部关节序号,分别表示髋关节、膝关节和踝关节,i=4时表示机器人足端,zmi为沿关节旋转方向坐标轴,xmi为沿连杆轴线方向坐标轴。L1、L2、L3分别为基节、股节、胫节长度。
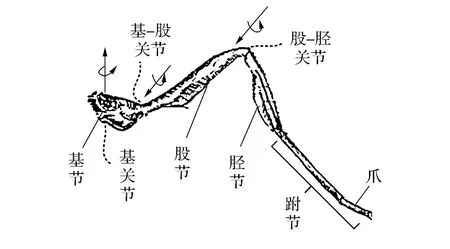
(a)蚂蚁腿部

(b)样机腿部
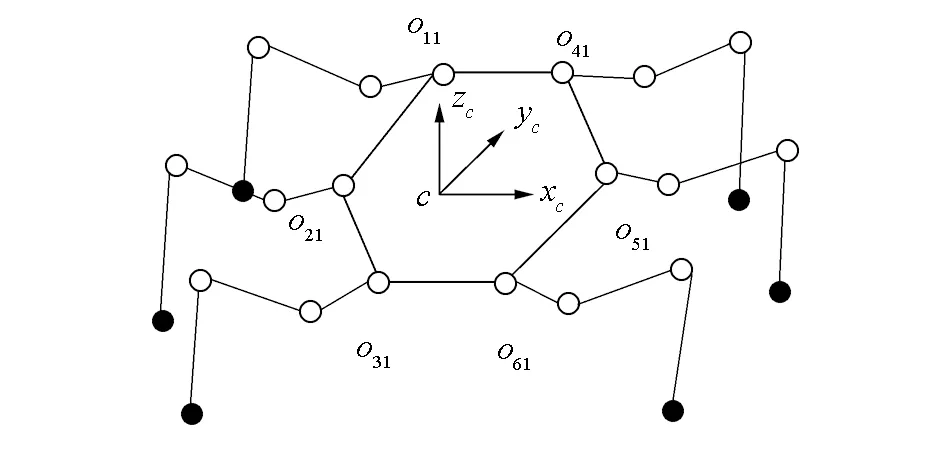
(a)躯干坐标系
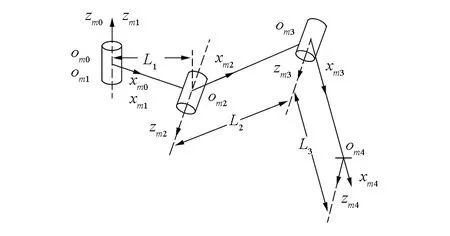
(b)单腿关节坐标系
1.2 正运动学分析
根据齐次坐标变换原理,通过齐次变换,可将机器人腿部基准坐标系∑om0变换到躯干质心坐标系∑c中,变换矩阵cTomo为
式中:(xom0,yom0,zom0)为机器人腿部基坐标系到躯干质心坐标系的平移坐标值,φ为腿部基坐标系∑om0到躯干质心坐标系∑c变换绕z轴的旋转角度。将表1中参数带入式(1)中,可以求得机器人腿部基坐标系与躯干质心坐标系之间的关系。
表1 基坐标系到躯干质心坐标系变换参数
Table 1 Transformation parameters of base coordinates to geocentric coordinate system
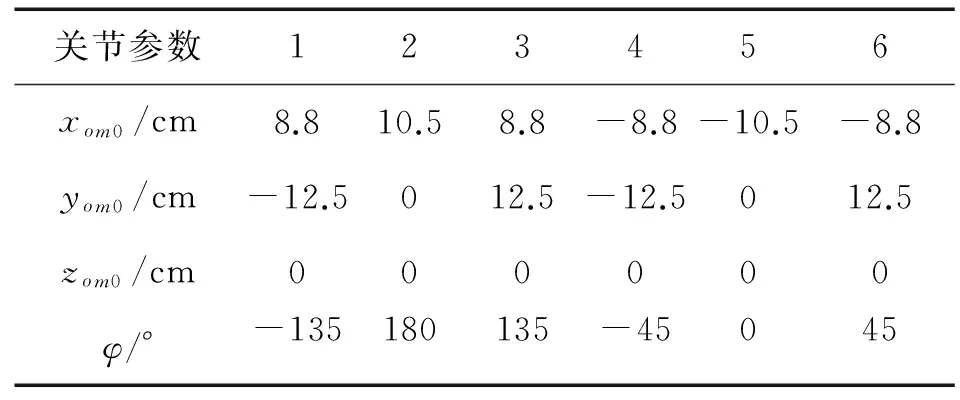
关节参数123456xom0/cm8.810.58.8-8.8-10.5-8.8yom0/cm-12.5012.5-12.5012.5zom0/cm000000φ/°-135180135-45045
机器人右侧腿部机构D-H参数如表2所示,θi表示第i个关节的转动角度。左侧腿D-H参数,除1=-π2,其他参数与右侧腿一致,均保持不变。

表2 右侧腿部机构D-H参数表
根据D-H坐标变换法[10],机器人足端点坐标系∑om4在躯干质心坐标系∑c中的位姿为
可求得右侧腿的运动学正解为
左侧腿的运动学正解为
1.3 六足机器人三角步态描述
步态指机器人的每条腿按一定顺序和轨迹的运动形式,包括通过调整迈步顺序和频率来调整身体的位姿[11]。
步态周期T为机器人完成一次完整步态所需要的时间。机器人单腿的迈步幅度称为步长。占空比为单腿在一个步态周期内,处于支撑相的时间在整个步态周期中所占比例,用字母γ表示。
六足机器人步态通常按照与地面接触脚的数目来划分。常见有三角步态、跟导步态和波动步态。三角步态是昆虫稳定行走时速度最快的一种步态。图3为一个步行周期内六足机器人的三角步态支撑相与摆动相示意图。白色表示摆动相,黑色阴影表示支撑相,腿1、腿3、腿5为一组,腿2、腿4、腿6为一组,同组腿相位相同,异组腿相位相差π。机器人行走时占空比分为3种情形:1)γ=0.5,即每条腿的支撑与摆动时间相等,一组腿支撑,另一组腿摆动(见图3(a));2)γ>0.5,即每条腿支撑时间大于摆动时间,6条腿出现同时着地的情况(见图3(b)),此种情况下,机器人稳定性较高,但速度较慢;3)γ<0.5,即每条腿支撑时间小于摆动相时间,6条腿出现同时悬空状况(见图3(c)),显然,这一情况机器人速度快但稳定性欠佳。占空比对爬行速度有直接影响。本文选择占空比为0.5的三角步态作为研究对象。
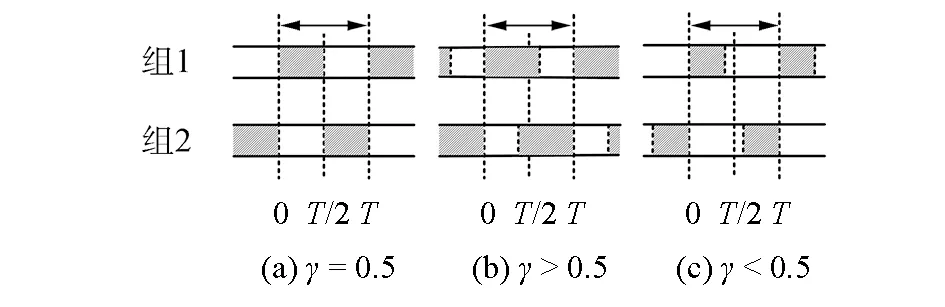
图3 六足机器人三角步态支撑相与摆动相示意图
2 CPG振荡器网络模型与仿真
2.1 CPG振荡器模型
中枢模式发生器(central pattern generator, CPG)是一种离散神经网络,能够产生复杂的高维信号控制动物的节律运动[12]。机器人学上,CPG通常被看作耦合动态系统,即非线性振荡器模型。CPG神经元的自发振动性与传统的机械振动类似,是通过采用互相连接的单个或者多个非线性振荡器来模拟CPG产生信号。其中非线性振荡器都有极限环,若极限环稳定,系统中所有的轨迹都会接近该极限环,这样即使系统中有小的扰动,系统也能回到稳定状态。
Hopf振荡器存在一个稳定的极限环,邻域中的轨线都螺旋趋近该极限环,具有很好的稳定性。与传统Hopf振荡器相比,本文采用改进的Hopf振荡器作为机器人信号发生器,不仅可以实现幅值频率可调,还可以独立调节支撑相与摆动相的相位关系,易于实现六足机器人腿部控制。其数学模型为
令x=rcosφ,y=rsinφ,γ=ωt,极坐标形式为


(a)μ变化的平衡点与极限环图
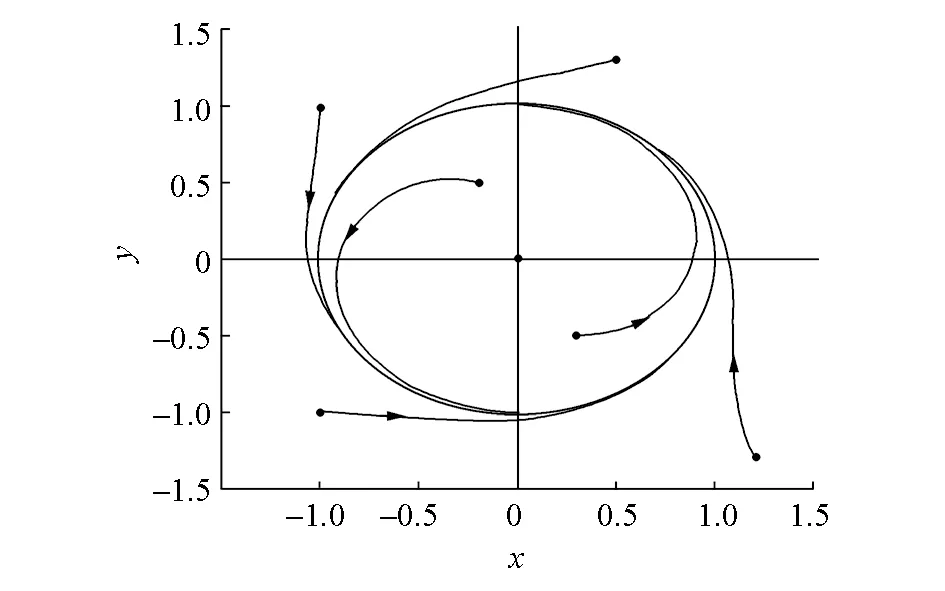
(b)x与y的相平面图
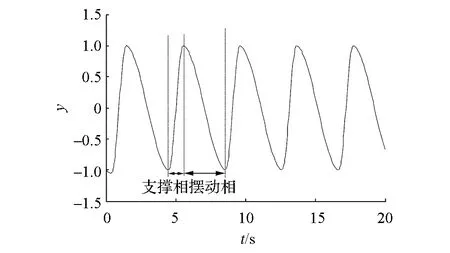
(c) 输出y的振荡曲线
由图4(c)可见,该振荡器能自发地产生稳定的周期振荡信号,方便调节上升和下降时间,从而很好地模拟了生物系统中的CPG神经元。
要实现六足机器人腿部之间的协调运动,需要振荡器的相互耦合,保证运动的同步性与协调性。耦合关系为
2.2 环形CPG网络模型构建
六足机器人的CPG网络拓扑结构由6个CPG单元构成,每个CPG单元对应六足机器人的一条腿,由Hopf振荡器组成。采用加权有向图构成网状结构,6个CPG单元作为有向图的6个顶点,相邻顶点之间采用全对称的双向连接。CPG网络拓扑结构如图6所示,在三角步态下,将腿分成{1,3,5}和{2,4,6}两组。同组腿相位相同,异组腿相位相反。
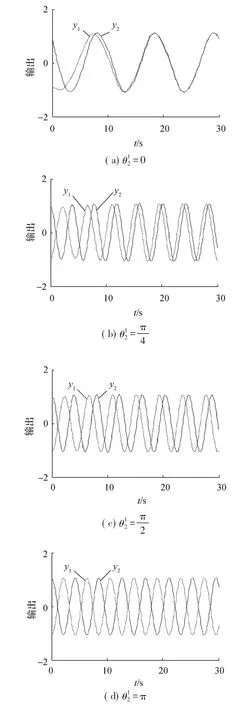
图5 两个耦合振荡器不同相位差输出波形图
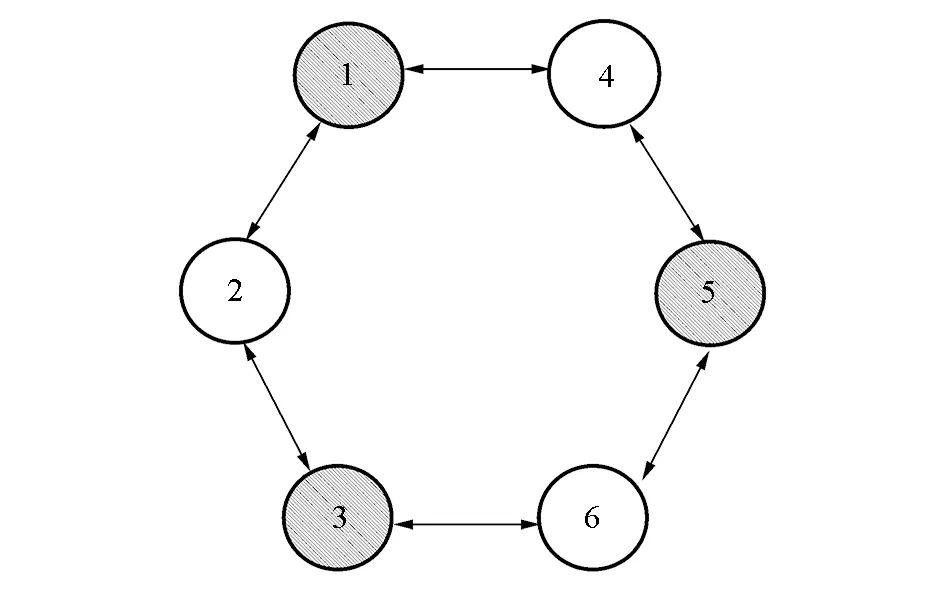
图6 环形CPG网络拓扑结构图
2.3 关节轨迹设计方案
六足机器人行走过程中,单腿关节角度具有如下规律:1)摆动相时,腿向前摆,髋关节角度增大,膝关节先正转再反转回到平衡位置,膝关节角度先增大后减小,踝关节转角与膝关节变化规律相同;2)支撑相时,腿后摆,髋关节角度减小,膝关节与踝关节角度几乎保持不变。
机器人有6条腿18个关节,如果每个关节都采用1个振荡器,需要18个振荡器,会使CPG网络过于复杂,非线性微分方程阶数过高,不利于CPG网络的参数优化和求解。
机器人在运动过程中,各关节之间相互配合,具有一定联系。为了简化模型结构,采用膝踝映射函数,根据踝关节的转角得到膝关节的转角。单腿CPG控制规律如下:1个CPG单元对应2个Hopf振荡器,输出信号相互耦合,分别控制髋关节、踝关节,膝关节信号通过膝踝映射函数得到。图7为2个Hopf振荡器生成的髋关节与踝关节的相位关系,其中y1为髋关节控制信号,y2为踝关节控制信号,调节两者频率值比为1:2,且两者保持固定的相位差。
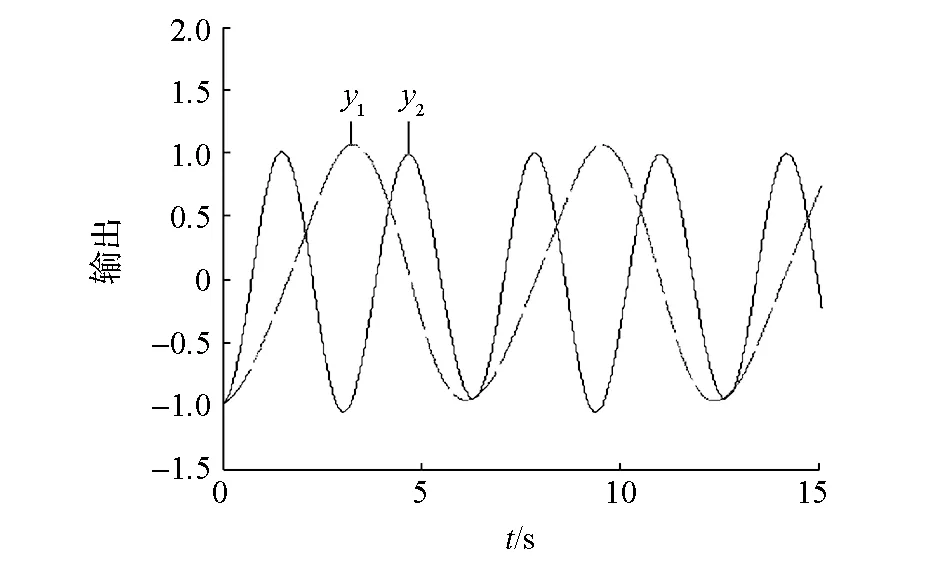
图7 三角步态髋关节、踝关节相位关系曲线
选取CPG模型髋关节输出曲线上升沿作为机器人摆动相,下降沿作为支撑相。根据机器人腿部摆动规律,对踝关节输出进行调整,在支撑相时调节参数,使踝关节输出趋向于零,符合实际规律。值得注意,两个振荡器耦合系数δ的取值会影响支撑相踝关节起始和末尾零值。当δ>1时,踝关节输出曲线振荡不符合正弦函数;当δ=0.35时,如图8,踝关节输出y21支撑相起始和结束位置数值有跳变;当δ=0.01时,踝关节输出y22支撑相基本趋于零值,关节输出平滑且趋于零。

图8 三角步态踝关节输出优化曲线
根据膝关节、踝关节的关节角度变化规律,将踝关节角度映射得到膝关节角度曲线,实现踝膝关节的耦合。单腿各个关节角度函数定义为
式中:k为比例系数,b为常数。调节k0、k1、k2、b1、b2使振荡器输出为髋关节、踝关节角度值。k3、k4、b3、b4为膝踝映射函数参数,参数b3、b4控制膝关节摆动幅度。
结合六足机器人机构参数,取k0=0.8,k1=0.78,b1=1.01,k2=0,b2=0,k3=0.78,b3=π/2,k4=0,b4=π/2。为了区分不同腿的不同关节角度,对每条腿的每个关节角度进行定义:用θij表示,其中i表示腿的序号(i=1,2,3,4,5,6),j=1表示髋关节,j=2表示踝关节,j=3表示膝关节。图9为三角步态下两条腿关节角度输出曲线,其中组{1,3,5}摆动角度用实线表示,以腿1作为示例;组{2,4,6}摆动角度用虚线表示,以腿2作为示例。两者相位相差为π。
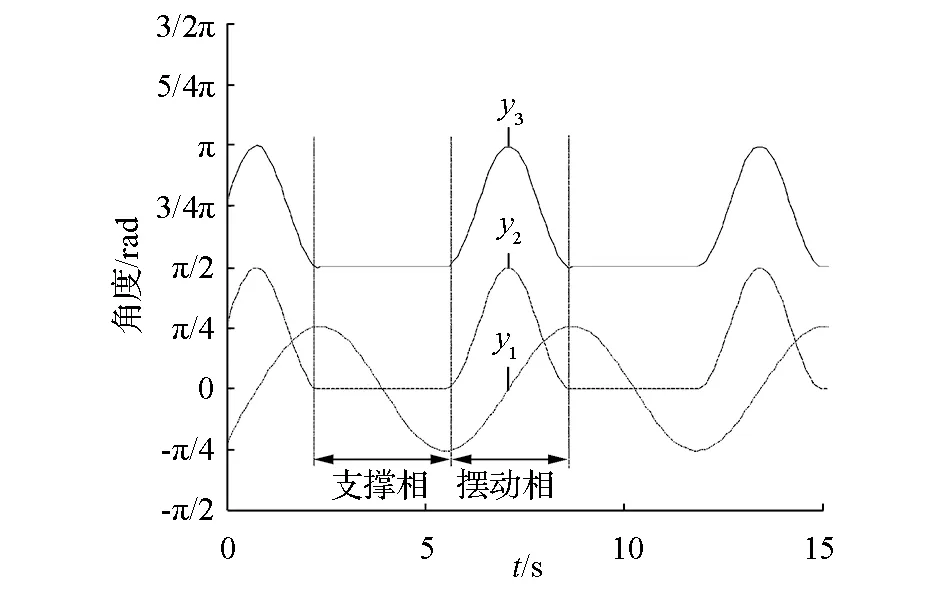
图9 三角步态单腿三关节输出曲线
根据前文正运动学分析,由机器人对应时刻各关节角度,可求出六足机器人足端位置轨迹,从而推出六足机器人三角步态下的理论步长。图10所示,点A1、A2、A3为机器人腿1在摆动相初始时刻髋关节、膝关节、踝关节角度,点B1、B2、B3为机器人腿1在摆动相结束时刻髋关节、膝关节、踝关节角度,A1=-0.796,A2=0.004,A3=1.58,B1=0.804,B2=0.008,B3=1.58,带入(4)式,求得六足机器人理论步长为17.25 cm。

图10 三角步态多足耦合三关节角度曲线
3 实物样机验证
为验证基于Hopf振荡器的六足机器人步态调节算法的有效性,本文搭建了六足机器人实验平台。六足机器人样机采用KST X20-8.4-50伺服舵机驱动,控制器为Arduino USB 32路伺服舵机控制器。主要包括显示模块、无线通讯模块、MPU6050模块、舵机控制模块。设计仿照六足蚂蚁的腿部比例,表3为六足机器人主要参数。其中,基节L1长度为髋关节到膝关节轴线距离;股节L2为膝关节到踝关节轴线距离;胫节L3为踝关节到足端的轴线距离。

表3 六足机器人样机主要参数
图11为六足机器人三角步态行走实验。实验平台上,每个短黑线间隔为20 m,样机搭载液晶显示,显示当前步态类型、振荡器预设参数。实验结果表明,机器人运动平稳,步态协调。经测量,六足机器人实际步长约为13.2 m,平均速度为6.45 m/s, 100 m内直线运动略向左侧平移4 m。机器人行走步长与理论步长有一定偏差,原因主要由于机构设计髋关节预留空间不足,实际行走未达到理论角度,实验中为避免关节发生碰撞,实际髋关节摆动范围约为[-π/6, π/6]。

图11 六足机器人三角步态行走实验
4 结论
本文设计了一种六足机器人节律运动CPG模型,仿真和实验表明:
1) 加入膝踝映射函数,可实现对六足机器人关节节律运动设计,简化CPG耦合网络模型;
2) 本文设计的关节映射函数参数合适,关节运动之间的相位关系合理;
3) 本文设计的CPG网络能够稳定的生成机器人的运动关节角度,输出结果较好的符合六足机器人三角步态的相位要求。
下一步将利用Hopf振荡器相位可调优点,进行六足机器人步态转换研究,实现更复杂灵活的动作。
[1]JAN IJSPEERT A J. Central pattern generators for locomotion control in animals and robots: a review[J]. Neural networks, 2008, 21(4): 642-653.
[2]吴正兴, 喻俊志, 谭民. 两类仿鲹科机器鱼倒游运动控制方法的对比研究[J]. 自动化学报, 2013, 39(12): 2232-2242. WU Zhengxing, YU Junzhi, TAN Min. Comparison of two methods to implement backward swimming for a carangiform robotic fish[J]. Acta automatica sinica, 2013, 39(12): 2232-2242.
[3]WU Xiaodong, MA Shugen. Adaptive creeping locomotion of a CPG-controlled snake-like robot to environment change[J]. Autonomous robots, 2010, 28(3): 283-294.
[4]高琴, 王哲龙, 赵红宇. 基于Hopf振荡器实现的蛇形机器人的步态控制[J]. 机器人, 2014, 36(6): 688-696. GAO Qin, WANG Zhelong, ZHAO Hongyu. Gait control for a snake robot based on Hopf oscillator model[J]. Robot, 2014, 36(6): 688-696.
[5]SEO K, CHUNG S J, SLOTINE J J E. CPG-based control of a turtle-like underwater vehicle[J]. Autonomous robots, 2010, 28(3): 247-269.
[6]LIU C J, FAN Z, SEO K, Fan Z, et al. Synthesis of matsuoka-based neuron oscillator models in locomotion control of robots[C]// IEEEProceedings of the Third Global Congress on Intelligent Systems (GCIS), 2012 Third Global Congress, Wuhan, China, 2012: 342-347.
[7]MATSUOKA K. Sustained oscillations generated by mutually inhibiting neurons with adaptation[J]. Biological cybernetics, 1985, 52(6): 367-376.
[8]FUKUOKA Y, KIMURA H, COHEN A H. Adaptive dynamic walking of a quadruped robot on irregular terrain based on biological concepts[J]. The international journal of robotics research, 2003, 22(3/4): 187-202.
[9]YU Junzhi, TAN Min, CHEN Jian, et al. A survey on CPG-inspired control models and system implementation[J]. IEEE transactions on neural networks and learning systems, 2014, 25(3): 441-456.
[10]BREAKSPEAR M, HEITMANN S, DAFFERTSHOFER A. Generative models of cortical oscillations: neurobiological implications of the Kuramoto model[J]. Frontiers in human neuroscience, 2010, (4): 190-14.
[11]JAN IJSPEERT A J, CRESPI A, RYCZKO D, et al. From swimming to walking with a salamander robot driven by a spinal cord model[J]. Science, 2007, 315(5817): 1416-1420.
[12]RIGHETTI L, JAN IJSPEERT A J. Pattern generators with sensory feedback for the control of quadruped locomotion[C]//Proceedings of IEEE International Conference on Robotics and& Automation. Pasadena, CA, USA, 2008: 819-824.
[13]MARK W. SPONG, S. HUTCHINSON, M. VIDYASAGAR. Robot modeling and con trol[M]. Hobokon, New Jekey, USA: John Wiley and Sons Inc., 2005: 65-74.
[14]于海涛. 基于非线性振子的 CPG 步态生成器及其运动控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009: 10-11. YU Haitao. Research on CPG gait generator based on nonlinear oscillator and its locomotion control[D]. Harbin, China: Harbin Institute of Technology, 2009: 10-11.
[15]FRIGON A, ROSSIGNOL S. Experiments and models of sensorimotor interactions during locomotion[J]. Biological cybernetics, 2006, 95(6): 607-627.

任杰,女,1990年生,硕士研究生,主要研究方向为仿生机器人运动控制。

徐海东,男,1991年生,硕士研究生,主要研究方向为仿生机器人运动控制。

王斌锐,男,1978年生,博士,教授,主要研究方向为仿生机器人及其智能控制。
2017年IEEE先进智能机电一体化国际会议
The 2017 IEEE International Conference on Advanced Intelligent Mechatronics
July 3-7, 2017, Munich, Germany
The 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM 2017) will be held on July 3-7 in Munich, Germany. The AIM 2017 conference brings together an international community of experts to discuss the state-of-the-art, new research results, perspectives of future developments, and innovative applications relevant to mechatronics, robotics, control, automation, and related areas.
The sponsors and organisers of AIM 2017 invite a submission of high quality mechatronics research papers describing original work, including the following topics: Actuators, Automotive Systems, Bioengineering, Data Storage Systems, Electronic Packaging, Fault Diagnosis, Human-Machine Interfaces, Industry Applications, Information Technology, Intelligent Systems, Machine Vision, Manufacturing, Micro-Electro-Mechanical Systems, Micro/Nano Technology, Modeling and Design, System Identification and Adaptive Control, Motion Control, Vibration and Noise Control, Neural and Fuzzy Control, Opto-Electronic Systems, Optomechatronics, Prototyping, Real-Time and Hardware-in-the-Loop Simulation, Robotics, Sensors, System Integration, Transportation Systems, Smart Materials and Structures, Energy Harvesting and other frontier fields.
Website: http://www.aim2017.org/
CPG model design based on hopf oscillator for hexapod robots gait
REN Jie, XU Haidong, GAN Su, WANG Binrui
(College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China)
The key to bionic motion is a central pattern generator (CPG), which realizes the crawl gait of a hexapod. Firstly, the coordinate system of the robot was set up and the associated forward kinematics were solved based on D-H parameters. Hopf oscillators were then adopted into the design of coupling models involving multiple legs. A CPG ring topology structure was established using six CPG units, with each CPG unit consisting of two coupled Hopf oscillators, which output the hip and ankle joint signals, respectively. In order to control each joint (of a hexapod robot), a knee-ankle mapping function was used. The function mapped the output of the ankle to joint angles for both the knees and ankles. The number of oscillators in the CPG network was reduced using this method. Meanwhile, the coupling coefficient was changed to guarantee the phase interlock of adjacent oscillators and give a stable and smooth signal. Finally, a physical prototype was constructed for testing the robotic gait. The simulations and test results show that this CPG network has a stable phase difference, which ensures that hexapod robot can walk stably in a triangular gait and a crawling speed of approximately 6.45 cm/sec can be achieved.
central pattern generator; Hopf oscillator; hexapod robots; kinematic analysis
2016-01-28.
日期:2016-09-21.
国家自然科学基金项目(51575503);浙江省自然科学基金项目(LY14F030021).
王斌锐. E-mail:wangbinrui@163.com.
TP242
A
1673-4785(2016)05-0627-08
10.11992/tis.201601036
http://www.cnki.net/kcms/detail/23.1538.TP.20160921.1116.002.html
任杰,徐海东,干苏,等.基于Hopf振荡器的六足机器人步态CPG模型设计[J]. 智能系统学报, 2016, 11(5): 627-634.
英文引用格式:REN Jie, XU Haidong, GAN Su, et al. CPG model design based on hopf oscillator for hexapod robots gait[J]. CAAI transactions on intelligent systems, 2016,11(5): 627-634.
