航天器大型柔性太阳翼挠性形变视觉测量优化设计
2016-12-24郎燕,于丹,刘鹏
郎 燕,于 丹,刘 鹏
(1.北京控制工程研究所,北京100094;2.哈尔滨工业大学模式识别研究中心,哈尔滨150001)
航天器大型柔性太阳翼挠性形变视觉测量优化设计
郎 燕1,于 丹1,刘 鹏2
(1.北京控制工程研究所,北京100094;2.哈尔滨工业大学模式识别研究中心,哈尔滨150001)
精确辨识出太阳翼的挠性参数有助于修正太阳翼动力学模型,为航天器控制系统的优化设计提供依据。基于非接触方式的在轨双目视觉测量可以最大程度保留太阳翼的完整性和功能性。讨论了美国、俄罗斯开展的太阳翼视觉测量在轨试验和标志物选择情况,针对未来航天器大型柔性太阳翼形变的在轨测量需求,设计了一种兼顾大视场和高精度的两组双目相机测量方案,给出了一种快速、高可靠地目标点检测和匹配算法,仿真结果表明该算法可有效提高测量精度。针对阴影区中不同照明条件下的标志点尺寸和材料的选择进行了试验研究,为在轨验证提供了依据。最后分析了不同观测角度时目标点的测量误差。
大型柔性太阳翼;挠性形变;在轨测量;双目视觉
1 引言
太阳翼上的太阳能电池阵为航天器提供正常工作所必需的能源。在航天器轨道控制和姿态控制过程中,推力器或控制力矩陀螺的工作使得太阳翼会产生挠性变形[1]。随着航天技术的发展,平台设备和载荷设备对整星功率需求越来越大,因此太阳翼尺寸也越来越大。在整星质量和功率的双重约束下,采用复合材料的大型柔性太阳翼已经开始应用[2],这使得航天器的挠性变形越来越大,振动基频越来越低,对控制系统的精度和稳定性提出了更高要求[3]。而过大的太阳翼形变还可能会对太阳翼的结构造成破坏[3⁃4],精确辨识出太阳翼的挠性参数(如固有频率、模态振型、阻尼等)有助于修正太阳翼动力学模型,为航天器控制系统的优化设计提供依据。由于太阳翼展开后面积大,在地面无法构建满足尺寸要求的真空微重力环境,所以在轨测量太阳翼形变量是实现太阳翼动力学模型辨识的有效手段。
美国NASA于1998年在哈勃空间望远镜SM⁃2任务中利用视觉对哈勃太空望远镜太阳翼的静态位置和动态响应进行测量。采用双目相机拍摄图像(静态位置测量)或者图像序列(动态响应特性测量),经过图像处理和三角解算得到特征点的三维坐标[4]。类似任务还包括NASA对和平号空间站一处舱体搭载的太阳翼系统参数的在轨测量[5]。该任务使用六台相机组成的双目视觉系统拍摄太阳翼的根部和末端的图像序列,利用三角解算得到目标点相对于时间的坐标序列,并利用特征系统辨识算法解出了太阳翼的系统特性,包括振动频率与阻尼等物理量[4]。
对于在轨试验中待观测太阳翼标志物特性的选择也有可供参考的研究结论。一种常见的方法是将反射性材料(如角反射器)制成的目标点贴在被测材料上[6],成像时这些点会在图像中成为白色亮点,计算时利用这些亮点进行匹配。但这一方法的缺点是对光照敏感,只有入射光与相机的光轴的夹角较小时才能获得良好对比度的图像,否则会无法识别。另一种人工标记点是使用白色材料,例如普通的白纸:地面测试表明采用白纸能够取得较好的效果,不会在相机光轴与入射光夹角较大时无法检测到目标[7]。此外,结构光测量的方法也被用于目标点的生成,即用投影设备将目标点投射在被测材料上进行测量[8],这一方法不会对被测材料产生影响,但是只适用于漫反射材质,且透射率和吸收率小的被测材料。
已报道的空间试验都采用了典型的双目视觉测量方法。由于太阳翼材料和结构的特殊性,使用接触式测量的方法(如加速度传感器)会导致电气结构复杂,检测位置少,同时给太阳翼带来明显附加质量[4]。使用基于视觉测量的非接触式方法,通过获知太阳翼上人工标志点或其自身的纹理位置来判断形变大小,这种测量方式对被测对象的影响最小,能够在最大程度上保留太阳翼的完整性和功能性[5]。
针对我国未来大型柔性太阳翼形变的在轨测量需求,本文提出一种基于大、小视场的两组双目视觉相机的测量方案,分别观测太阳翼的不同区域:小焦距相机组拍摄太阳翼近端图像,大焦距相机组拍摄太阳翼远端图像,拍摄到的两组图像能够覆盖整个太阳翼。从而兼顾大视场和高精度。为提高双目相机的在轨测量计算速度和可靠性,给出一种新的目标点检测和匹配方法,以提高太阳翼变形的测量精度。针对阴影区下不同照明条件下标志点的尺寸和材料的选择进行试验,并推导了不同观测角度时目标点的测量误差。
2 太阳翼形变视觉测量方案
2.1 双目相机的布局
对于单侧尺寸为12 m×5 m的大型柔性太阳翼阵面,试验条件列于表1。

表1 试验输入条件Table 1 Simulation parameters
双目相机的布局原则包括以下几点:
1)标志点尽量在图像的中央,减少镜头光学畸变的影响;
2)每组相机左右图像应保证较大的公共区域;
3)保证近场和远场图像也存在适当的公共区域,便于在太阳翼形变时视觉测量仍能覆盖太阳翼的全部区域;
4)近场图像可计算的目标点个数和远场图像可计算的目标点个数之和需大于标志点数量;
5)在太阳翼绕根部旋转±1°时,仍保证以上性质。
编写仿真程序,输入相机参数与太阳翼参数生成理想的拍摄图像,最终得到了表2所示的合适的相机内外参数,仿真图像结果如图1所示。
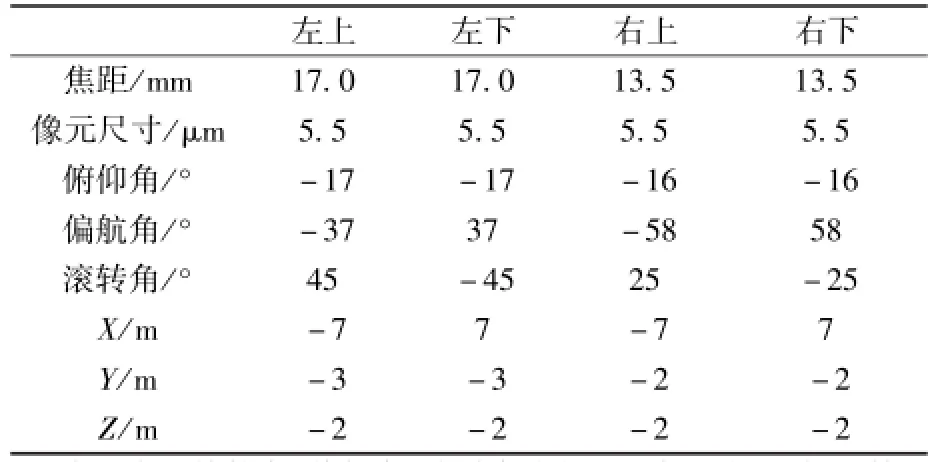
表2 相机优化布局结果Table 2 Optimal camera configurations

图1 太阳翼上标志点仿真成像图像Fig.1 Imaging simulation of markers on solar arrays
2.2 标志点检测和提取优化算法
针对图1的仿真图像,可结合相机内外参数解出各个点的三维坐标[9⁃11]。给定相机参数和仿真图像,计算标志点三维坐标的基本步骤为:1)在图像上计算出各个标志点几何中心的图像坐标(目标点检测);2)根据极线约束匹配左右图像目标点(目标点匹配);3)三维坐标重构。
2.2.1 标志点检测
根据本试验先验知识:标志点之间的距离已知。因此采用预报⁃校正法来提取目标点。
计算标志点在图像中坐标的步骤如下:
1)如图2所示,假设三个点X1、X2、X11为太阳翼处于任何位置时变形最小的点,它们在近场左相机图像上的像点分别为x1、x2、x11。根据标定的左相机外参数、内参数和目标点在全局坐标系中的坐标位置,估算x1、x2、x11在图像中的三个初始估计位置。分别在三个初始位置附近用25×25的高斯模板搜索目标点,并计算匹配区域的质心坐标,记为和(为了计算方便,X1、X2、X11选择图像上部分的点。)
2)计算直线x1x2的方程,记为y=l1x+b1,计算x1、x2两点在图像上水平方向的增量Δx1=x2-x1。

图2 近场左相机中目标点检测Fig.2 Marker recognition of the left near field camera
3)在图像上估计x2点的位置。计算+Δx1和以为中心计算15×15窗口区域的质心,记为
6)在图像上估计x3的位置。计算和以为中心计算15×15窗口区域的质心,记为
8)更新直线方程和水平方向位移量。用点(x′3,y′3)和(x′2,y′2)更新直线方程y=l3x+b3和位移量Δx′3=x′3-x′2。
9)用上述方法计算当前行上其他点在图像上的位置坐标,如果在搜索过程中失败,用直线估计位置点作为目标点检测位置。
10)估计下一行第一个点的方法与水平方向估计第二个点的方法相同,即估计x11位置使用的方法与在水平方向上估计x2位置的方法相同。
11)在下一行第一个点和第二个点之间的直线方程使用上一行第一个点和第二个点之间的直线平移到下一行第一个点的直线方程替代,即x11x12与x1x2平行。
12)下一行其他点位置的方法与估计上一行其他点位置的方法相同。
用这种方法,可以得到两幅图像所有标志点的图像坐标。该方法的优点为:
1)计算速度快。每一个标志点质心位置的计算都是将已经得到的标志点的质心位置及其在图像上的直线关系作为先验知识的,搜索在较小的区域中进行。2)可靠性高。在局部范围内太阳翼变形量较小,连续三个标志点近似在一条直线上的假设是成立的。另外,在太阳翼展开过程中标志点脱落或移位,该方法仍然有效。
2.2.2 标志点匹配
根据极线几何的知识,求出基础矩阵F,计算左右图像的对应点xl、xr是否满足其中等于零的条件在实际中可放宽为小于某个阈值。用这样的方法,匹配出两图像中的对应点。
在实际测量中,基础矩阵F在相机标定时可直接求解,并作为参数装订到视觉测量系统中,不需要在轨计算。设令标志点数量为N,求解以下方程组便可解出基础矩阵F。

在图像上对点的检测存在噪声是典型的情形。通常情况下,正确的点应该在检测点附近,,但
校正前后测量精度的对比列于表3中。在校正前,测量精度随图像中噪声能量的增加快速下降,校正后,测量精度得到明显改善,特别是在噪声能量较大时这种改善效果更加明显。
2.2.3 两组双目相机系统中标志点的提取
基于太阳翼根部在任何情况下变形较小的假设,预报⁃校正法检测目标点对于太阳翼根部的图像是完全适用的。然而对于末端的两幅图像,由于发生形变时标志点本身的位置相对于根部有较大变化,因此直接使用零位坐标应用预报⁃校正法可能会有较大的误差,甚至检测不到目标点。对于这个问题,可以利用远近场图像存在较大公共区域这一特性,使用如下方法进行标志点检测:
1)首先计算出近场两幅图像重叠区域所有标志点的三维坐标。
2)选择近场图像和远场图像重叠区域中的一组满足直角关系的三个目标点。用近场双目视觉相机计算这三个标志点在太阳翼坐标系中的坐标。例如图3左图选择的三个点。
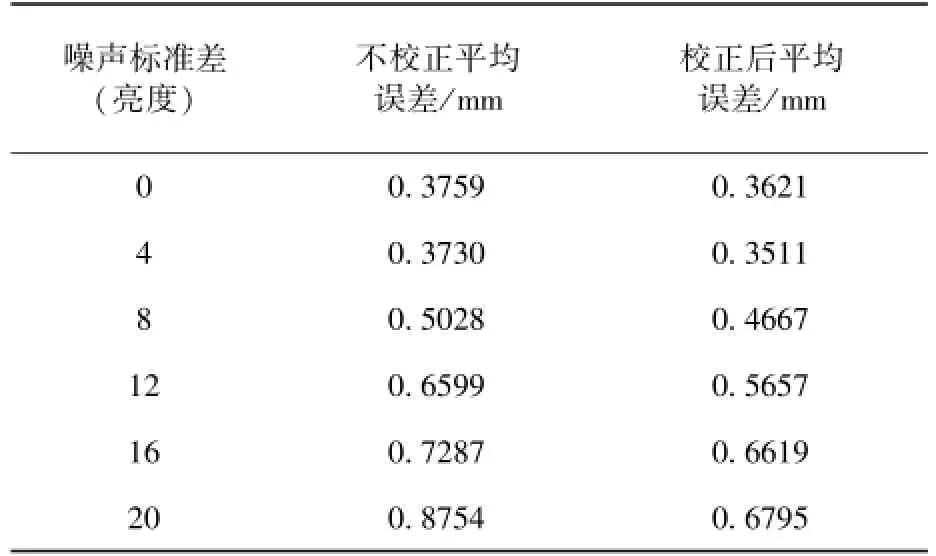
表3 校正对测量精度的改进Table 3 Effects of calibration on measurement accuracy
3)根据远场相机的内外参数,以及三个标志点在太阳翼坐标系下的坐标,经过反向投影得到这三个标志点在远场相机图像中的初始位置,如图3右图所示。
4)利用这三个图像坐标作为预报⁃校正法的起始参考点,计算出远场图像其余标志点的图像坐标。
同理,计算出右相机图像对应的目标点,根据三角解算重构出这些标志点的三维坐标,结合近场相机得到的坐标,便可得到太阳翼上所有标志点的坐标。该方法在太阳翼零位以及末端位移不超过100 mm的情况中得到了准确的测量结果。
2.3 照明条件与标志点材料的选取
为了避免杂光影响,考虑在阴影区进行双目相机的测量。确定合适的照明条件以及良好的标志点材料是必要的。针对这一需求,进行了相关试验,通过使用不同功率的LED照明以及不同材料的标志点,确定了优化的照明+标志点组合。
试验选择在夜晚进行,光源、相机和标志的空间位置如图4所示。
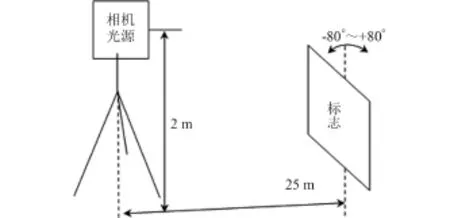
图4 实验器材布局Fig.4 Layout of equipment in the experiment
候选的材料包括:3M反光膜、玻璃微球反光带、白纸、白色硅胶,其中3M反光膜和玻璃微球反光带都用反光粉作为反射材料,反光粉的成分包括SiO2、CaO、Na2O、TiO2、BaO等。将候选材料裁剪成圆形和方形贴在太阳翼表面材料(Kapton薄膜)上,布局如图5所示。

图5 标志点布局和材料Fig.5 Layout and material of the markers
图6给出了成像试验结果。其中,(a)为标志板在0°位置拍摄的局部放大图像,距离25 m,白纸标志和硅胶标志没有成像,3M反光胶带成像较暗,玻璃微球反光带清晰成像。(b)为标志板在-30°位置拍摄的局部放大图像,距离25 m,白纸标志和硅胶标志没有成像,3M反光胶带成像较暗,运动用反光带清晰成像,表面覆盖一层kapton膜的反光带亮度变的更暗,其他反光带的亮度也下降了。(c)为标志板在-60°左右位置拍摄的图像和局部放大图像,距离25 m,白纸标志和硅胶标志没有成像,3M反光胶带不能可辨识地成像,运动用反光带可以成像,表面覆盖一层kapton膜的反光带亮度变的几乎不可见,其他反光带亮度也下降了,但可辨识。(d)为标志板在-80°左右位置拍摄的图像,所有标志点都不能成像。

图6 成像实验结果Fig.6 Experimental results of imaging
试验结果表明,使用11W LED作为光源,当光轴与目标坐在平面法线夹角60°以内时,玻璃微球反光带可以成像,3M反光胶带成像的角度范围小,其他材料标识器不能成像。对于LED光源,每瓦需要提供6 cm2的散热。
2.4 标志点大小估计
由于目标点具有一定质量,所以需要尽量减少目标点的体积以降低附加质量对太阳翼材料的影响,同时也需要保证在拍摄的图像中能够检测到目标点,不至于目标点太小而造成较大误差。因此需要找到一个适当的标志点半径,使得在生成的图像中最小的椭圆短轴在10个像素左右。
通过仿真实验,指定标志点半径,在标志点圆周上指定一些点,经过透视投影变换,得到图像上取点的分布,统计椭圆长轴和短轴近似的最大值和最小值。仿真结果表明,标志点半径为10 cm时,椭圆短轴长大约占8个像素,符合限制条件。
进一步,在真实的情况下还可以通过减小标志点的数目、改变标志点间距等方法降低标志点质量对太阳翼的影响。
2.5 标志点检测误差
目标点为圆形,经透视投影变换后,在图像中以椭圆的方式体现。根据文献[8],图像上椭圆的中心和圆形标志点的中心在图像上的投影并非是重合的。因此,透视投影变换下圆形标志点在像平面上的畸变误差也需要考虑。

图7 空间椭圆透视Fig.7 Spatial elliptical perspective
如图7所示,椭圆O1A1B1C1D1在平面π上的投影为椭圆Γ,相机焦距f,坐标系Oxyz与O′x′ y′z′间通过旋转矩阵R=[ri](i=1,2,…,9)变换,α、β、γ为O′O1在O′x′y′z′的方向角,φ为O′B2与x′正方向逆时针夹角,同时设θ=∠A1O′O1=∠C1O′O1,定义ϕ角如下式:

椭圆Γ的方程为下式:

因此中心坐标为:

由于这里椭圆所占的像素面积较小,采用质心法求取椭圆的几何中心,并假设这种方法的结果就是上述求得的坐标值。而空间椭圆O1A1B1C1D1的中心O1在平面π上的投影坐标为:

可以看出空间椭圆中心的投影和投影椭圆的中心存在偏差,设这种畸变误差为二者坐标的欧氏距离,通过计算可知当空间椭圆与图像平面的夹角为0°、99°、180°时,畸变误差为零。此外圆形目标成像后,图像上椭圆越小,畸变误差就越小。所以,应该结合照明条件、图像处理方法对标志点的检测能力等因素选择适当的标志点尺寸。在本文的仿真实验中,使用直径为10 cm的圆形标志点,成像后得到椭圆,畸变误差小于0.2个像素。
3 结论
通过在太阳翼上粘贴利用运动反光材料制成的标志点,并加以合适的照明条件,在黑暗条件下拍摄的图像中可以识别出各个标志点。根据误差分析的结果,左右相机的基线距为14 m时,可以得到较准确的测量结果。选择直径为100 mm的标志点,以本文说明的相机参数配置,成像目标的直径约为8个像素,可以被检测。通过检测到的标志点在图像中的坐标,利用双目视觉原理可以算出标志点的三维坐标,从而可以获得太阳翼的形变情况。
(
)
[1]屠善澄.卫星姿态动力学与控制(1)[M].北京;中国宇航出版社,1999:162⁃163.Tu Shancheng.Satellite Attitude Dynamics and Control(1)[M].Beijing:China Aerospace Press,1999:162⁃163.(in Chinese)
[2]杨巧龙,任守志,王举,等.柔性太阳翼技术发展现状及其关键技术研究[C]//可展开空间结构学术会议,西安;2014.Yang Qiaolong,Ren Shouzhi,Wang Ju,et al.Research on the development status and key technology of flexible solar wing technology[C]//Deployable Space Structure Confer⁃ence,Xi'an;2014.(in Chinese)
[3]许英健.航天器太阳翼动态影响测量系统的研究与设计[D].上海:上海交通大学,2012.Xu Yingjian.Research and Design of Dynamic Measurement System for Spacecraft Solar Wings[D].Shanghai:Shanghai Jiao Tong University,2012.(in Chinese)
[4]Sapp C A,Dragg J L,Snyder M W,et al.Photogrammetric assessment of the hubble space telescope solar arrays during the second servicing mission[R].NASA/TP⁃98⁃201793,NAS 1.60:201793,S⁃839,1998.
[5]Gilbert M G,Welch S S,Pappa R S,et al.STS⁃74/MIR photogrammetric appendage structural dynamics experiment preliminary data analysis[J].AIAA⁃1997⁃1168,1997.
[6]Juang J N,Pappa R S.An eigensystem realization algorithm for modal parameter identification and model reduction[J].Journal of Guidance,Control,and Dynamics,1985,8(5),620⁃627.
[7]Giersch L R M.Pathfinder photogrammetry research for ultra⁃lightweight and inflatable space structures[R].NASA/CR⁃2001⁃211244,NAS 1.26:211244,2001.
[8]P Pappa R S,Black J T,Blandino J R,et al.Dot⁃projection photogrammetry and videogrammetry of gossamer space struc⁃tures[J].Journal of Spacecraft and Rockets,2003,40(6):858⁃867.
[9]张广军.机器视觉[M].北京:科学出版社,2005:99⁃122.Zhang guangjun.Machine Vision[M].Beijing:Science Press,2005:99⁃122.(in Chinese)
[10]Zhang G,Wei Z.A position⁃distortion model of ellipse centre for perspective projection[J].Measurement Science and Technology,2003,14(8):1420.
[11]冯文灏.近景摄影测量[M].武汉:武汉大学出版社,2002:60⁃213.Feng Wenhao.Close⁃range Photogrammetry[M].Wuhan:Wuhan University Press.2002:60⁃213.(in Chinese)
[12]Gonzalez R C,Woods R E.Digital Image Processing[M].北京:电子工业出版社,2011:20⁃245.
Optimization Design of On⁃orbit Vision Measurement in Spacecraft Large Flexible Solar Arrays Deformation
LANG Yan1,YU Dan1,LIU Peng2
(1.Beijing Institute of Control Engineering,Beijing 100094,China;2.Harbin Institute of Technology,Pattern Recognition Research Center,Harbin 150001,China)
The precise identification of the flexible parameters of the solar arrays is helpful to modify the dynamic model of the solar arrays,which will provide a basis for the optimization design of the spacecraft control system.On⁃orbit binocular vision measurement based on non⁃contact mode can keep the integrity and function of the solar arrays to the maximum extent.First,the on⁃orbit solar arrays vision measurement experiments and the selection of markers in the United States and Russia were discussed in this paper.According to the needs of future spacecraft on⁃orbit measurement of large flexible solar array deformation,a two groups of binocular camera measurement scheme with large visual field and high precision was proposed,and a quick and reliable marker detection and matching algorithm was provided.The simulation results showed that the proposed algorithm could effectively improve the measurement accuracy.Then,experiments on the marker size and material were carried out with different lighting conditions in the shadow area which could provide a basis for the on⁃orbit verification.Moreover,the measurement error of the markers at different observation an⁃gles was analyzed.
large flexible solar arrays;flexible deformation;on⁃orbit measurement;binocular vision
V448.25
A
1674⁃5825(2016)06⁃0781⁃07
2016⁃05⁃27;
2016⁃11⁃10
国家自然科学基金(61672190)
郎燕(1981-),女,博士,高级工程师,研究方向为航天器控制系统设计。E⁃mail:yan.lang@126.com
