基于形态小波的核磁共振测井信号去噪及现场应用研究

2016-12-23蔡剑华黎小琴

地质与勘探 2016年1期

关键词：小波测井信噪比

蔡剑华，黎小琴，张勋

(湖南文理学院信息研究所湖南常德 415000)

地球物理

基于形态小波的核磁共振测井信号去噪及现场应用研究

蔡剑华，黎小琴，张勋

(湖南文理学院信息研究所湖南常德 415000)

核磁共振测井中采集到的回波串信号十分微弱,而背景噪声很强，使信噪分离困难。为解决这一问题，引入了结合数学形态学的特征识别和小波分解的多分辨率分析特性的形态小波方法。讨论了方法的数据基础和应用步骤，并与小波软阈值方法处理结果进行了对比分析。实测数据处理结果表明：形态小波去噪方法具有良好的细节保留和抗噪声能力，去噪效果优于小波软阈值滤波方法；在消除测井信号随机噪声的同时，能很好地保留信号的波形和特征，在较低信噪比下仍可有效地提取测井信号的有用信息，提高了T2谱的反演精度。

形态小波核磁共振测井小波软阈值去噪

Cai Jian-hua, Li Xiao-qin，Zhang Xun. De-noising of NMR logging signals based on the morphological wavelet and its real application[J]. Geology and Exploration, 2016, 52(1):0146-0151

核磁共振测井可以计算储层孔隙度、渗透率等主要的储层物理参数，还可以识别和评价储层流体及其性质，在石油勘探开发中有独特而重要的应用(肖立志等，2003)。核磁共振测井中横向弛豫时间 T2谱是由测得的回波串信号反演得到，再用T2谱估算储层孔隙中流体的物理参数，所以核磁共振测井信号的SNR决定着T2谱反演的精度，这种情况在SNR小的核磁共振测井中更加突出(Edwards，1996；翁爱华等，2003)。提高回波串信号的SNR，可改善核磁共振测井的精度，其有效措施就是对信号进行去噪的预处理。较成熟的核磁共振测井信号滤波算法有时间平均、有限冲击响应、小波变换、模态分解等方法(Edwards，1996；蔡剑华等，2010；吴磊等，2011)。本文结合数学形态学的特征识别和小波分解的多分辨率分析特性，提出将形态小波应用到核磁共振测井信号去噪中来。对回波串信号进行去噪处理，从而抑制噪声，突出有用信号的信息，最后对降噪后的信号进行T2谱的反演获得储层物理参数。本文研究了形态小波在测井信号分析领域的应用原理和方法，并与小波软阈值的滤波方法的降噪效果进行了对比，来验证该方法的可行性与有效性。

1 方法原理

1.1 形态小波

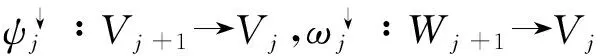
(1)

(2)

满足上述条件的分解为非对偶小波，分析与合成算子采用形态学滤波器就构成了形态小波(严家斌等，2008)。形态小波作为一种非线性小波，兼顾数学形态学的形态特征和小波的多分辨率特性，在去噪的同时具有良好的细节保留能力，能有效地保留信号的有用信息。

1.2 数学形态学基本变换

数学形态学的基本运算有：膨胀、腐蚀、开启和闭合，他们分别定义如下(Haoetal.，2009；沈路等，2010)：

定义1 设A为集合，B为结构元素，则A关于B的腐蚀变换定义为

AΘB={x:B+x⊃A}

(3)

定义2 设A为集合，B为结构元素，则A关于B的膨胀变换定义为

A⊕B=∪{x:A+b:b∈B}

(4)

定义3 设A为集合，B为结构元素，则A关于B的开变换定义为

(5)

定义4 设A为集合，B为结构元素，则A关于B的闭变换定义为

(6)

腐蚀、膨胀、开、闭这4种运算为形态学基本运算，速度很快。本文采用的形态小波是极大提升形态小波，预测和更新算子是基于极大值(膨胀)形态算子来构造的(沈路等，2010)。

1.3 小波阈值去噪

对于连续的情况，小波为(Donohoetal.，1994；蔡剑华等，2013)：

ψa,b(t)=|a|-1/2ψ((t-b)/a) a,b∈R,a≠0

(7)

式中：Ψ(t)为一个基本小波函数或母小波函数，a为伸缩(尺度) 因子；b为平移因子。任给函数f(t) ∈L2(R)，其连续小波变换及重构公式(逆变换) 为

(8)

(9)

对于离散情况，小波为(Donohoetal,1994,1995)：

ψj,k(t)=|a|-j/2ψ(2-jt-k)

(10)

与函数f(t)相应的离散小波变换系数及其重构公式为

(11)

(12)

式中：C是一个与信号无关的常数。根据小波变换的Mallat算法，对信号其进行分解，得到不同尺度上的小波系数Cj,k，再对Cj,k进行阈值处理，然后再进行重构得到新信号。本文采用常用的软阈值算法如下(Donohoetal.，1994，1995；Trad，2000)：

(13)

(14)

其中，N为信号长度，σ为噪声的方差(Donohoetal.，1995)

σ=MADj/0.6745

(15)

MADj为小波分解后第j层高子带系数的中值。可见，小波软阈值去噪是利用阈值处理信号经小波分解后的小波系数，去除由噪声引起的小波系数，保留由信号产生的小波系数，然后由处理后的小波系数进行小波反变换重构出去噪后的信号，软阈值去噪中，阈值的取值来自信号本身，较硬阈值方法能更多的保留有用信号。

2 方法步骤

形态小波能够实现信号形态特征和噪声的分离，具有在不同尺度上保留信号局部极大值的特性，非常适合从含噪的核磁共振测井信号中提取有用的成分。图1为基于形态小波的核磁共振测井信号去噪流程图，具体方法描述如下：

1) 先用形态小波对信号进行分解，对各尺度上细节信号进行软阈值降噪处理，保留包含局部极大形态特征的尺度信号。

2) 再用形态合成算子对阈值去噪后的信号进行重构，得到形态小波降噪后的信号。

3) 对降噪后的信号进行T2谱的反演获得储层物理参数。

3 去噪效果评价参数

图1 基于形态小波的核磁共振测井信号处理流程图

为了探讨本文方法对测井信号的去噪效果，采用了信噪比(SNR)、均方误差(RMSE)、曲线平滑度指数(SR)三项指标来对核磁测井信号去噪效果进行评估。SNR反映算法的去噪能力；去噪前后信号的幅值差异用RMSE来体现；SR用来衡量曲线的平滑程度。RMSE,SNR和SR的计算见(16)～(18)式所示(Goutsia，2000；闫常友等，2005；陈涛等，2008)。

(16)

(17)

(18)

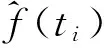
4 核磁共振信号处理

4.1 信号去噪

图2所示是一段实测的核磁共振测井的回波串信号。核磁共振测井的原始数据是幅度随时间衰减的回波信号，其数学模型为(蔡剑华等，2010)：

(19)

核磁共振测井采集到的回波串信号及其微弱，且井下环境噪声复杂，测井信号极易受环境噪声的干扰。由图2所示的实测回波串信号可以看出，信号受噪声的污染较大，信噪比低，信号的波形和峰值特征都被噪声淹没了。

图3对比了小波软阈值滤波和本文提出的形态小波处理的去噪结果。图4对比了原始测井信号和本文方法去噪后信号的时频谱图。从图3和图4可以看出：(1)两种处理结果相比，形态小波去噪算法对高频噪音的抑制效果要好，保持了原始信号的趋势，而且更加平滑。(2)核磁共振测井信号的低频部分是信号的主要部分，原始测井信号受高频的随机噪声干扰较大，信噪比较低；形态小波去噪后信号的时频图显示随机噪声得到了很大程度的抑制，而其含有有用信息的低频部分能量分布变化不大，信息得到了很好的保留，为反演出高质量的T2谱奠定了基础。

图2 原始核磁共振测井的回波串信号

4.2 去噪效果评价

为了验证形态小波相对小波软阈值滤波算法在分析核磁测井信号的有效性与优越性，采用了SNR、RMSE、SR三项指标来对测井信号去噪效果进行评估。表1分别列出了小波软阈值和本文去噪方法的3个评价参数的对照值。由表1可以看出：(1)小波软阈值滤波方法效果较好，去噪后SNR达到31.821，去噪后信号的RMSE仅为0.00507，SR为0.90785，而且特征保持的也相对较好，是相对较好的滤波方法。(2)本文提出的方法去噪效果较好，去噪后SNR达到35.793，RMSE仅为0.00237，SR达到了0.93142，且信号峰值特征保持较好，体现了本文方法良好的细节保持能力，非常适合于低SNR核磁共振测井信号的去噪。

为研究降噪前后T2谱分布的改善效果，分别用去噪前后的信号计算了T2谱分布，并比较了小波软阈值和形态小波处理后的结果。图5所示为去噪前后的T2谱分布。显然，噪声的影响得到了很大的改善，去噪后突出了反演曲线中被淹没的波峰信息。相比小波软阈值和形态小波处理后的结果，在反演的T2曲线中，形态小波处理后的T2谱分布，两个波峰更为明显。

图3 两种方法消噪后的回波串信号

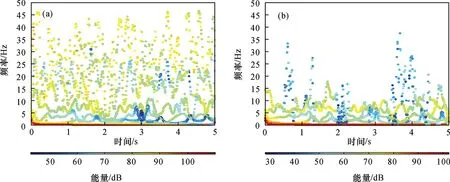
图4 消噪前后回波串信号的时频谱图

表1 两种去噪方法评价参数的比较

图5 消噪前后反演的T2谱

表2 去噪前后核磁测孔隙度结果对比

4.3 现场应用

采用本文方法和小波阈值方法分别对4个井8个不同段位的核磁测井信号进行了现场应用研究。表2给出了用去噪前后核磁信号反演得到的孔隙度结果。以水测孔隙度为真值，去噪前测得的孔隙度相对误差绝对值的平均值是4.8613%，小波软阈值去噪后测得的孔隙度相对误差绝对值的平均值是2.6737%，形态小波方法去噪后测得的孔隙度相对误差绝对值的平均值是1.8512%。可见去噪后大大提高了T2谱的反演精度,且形态小波方法要优于小波软阈值方法。

5 结论

核磁共振T2谱反演质量决定着核磁共振资料的应用效果，信噪比对T2谱反演质量影响较大，而核磁共振测井信号比较微弱，容易被环境等随机噪声干扰，信号噪声容易造成解的偏离。本文提出的形态小波去噪方法，结合了数学形态学和小波变换各自的优点，在消除背景噪声的同时，能很好地保留核磁共振测井回波串信号的波形和特征，去噪效果优于小波软阈值滤波方法，在较低信噪比下仍可有效地提取测井信号的有用信息，为反演出高质量的T2谱奠定了基础。

Cai Jian-hua,Wang Xian-chun,Hu Wei-wen.2013.De-noising of MT signal based on empirical mode decomposition and wavelet threshold method[J].Geophysical Prospecting,48(2):303-307(in Chinese with English abstract)

Cai Jian-hua,Tang Jing-tian，Hu Wei-wen.2010.A New De-noising Method of NMR Log Signals Based on Empirical Mode Decomposition [J].Nuclear Electronics & Detection Technology,30(3):389-393(in Chinese with English abstract)

Chen Tao,Li Bing-hai.2008.Removal of non-Gaussian stripe noise in images based on Wavelet[J].Geology and Exploration,1:19-27(in Chinese with English abstract)

Donoho D L.1995.De-noising by soft-thresholding[J].IEEE Transaction on Information Theory,41(3):613-627

Donoho D L,Johnstone I M.1994.Ideal spatial adaptation via Wavelet shrinkage[J].Biometrika,81:425-455

Edwards C.1996.Improved NMR well logs from Time dependent echo filtering [C].In 37th annual logging symposium transactions : Society of Professional Well Log Analysts:12

Goutsias J,Heiimans H J.2000.Nonlinear multi-resolution signal decomposition schemes-Partl: morphological pyramids[J].IEEE Transactions on Image Processing,9(11):1862-1876

Heijmans H,Goutsias J.2000.Nonlinear multi-resolution signal decomposition schemes-Part II; morphological wavelets[J].IEEE Transaction on Image Processing,9 (11):1897-1913

Hao Ru-jiang,Chu Fu-lei.2009.Morphological undecimated wavelet decomposition for fault diagnostics of rolling element bearings[J].Journal of Sound and Vibration,320(4-5):1164-1177

Shen Lu,Zhou Xiao-jun,Liu Lie.2010.Application of Morphological Wavelet De-noising in Extracting Gear Fault Feature[J],Transactions of the Chinese Society for Agricultural Machinery,41(4):217-221(in Chinese with English abstract)

Trad D O,Travassos J.M.2000.Wavelet filtering of magnetotellurie data[J].Geophysics,65:482-491

Weng Ai-hua，LiZhou-bo,Mo Xiu-wen.2003.Processing of low signal/ noise ratio NMR logging data[J].Journal of Ji Lin university(earth science edition),33(2):232-235(in Chinese with English abstract)

Wu Lei,Kong Li,Cheng Jing-jing.2011.Signal De-noising Algorithm Design in NMR Logging Based on Wavelet Transform[J].Instrument Technique and Sensor.10: 71-73(in Chinese with English abstract)

Xiao Li-zhi，Xie Ran-hong.2003.Applications of NMR to oil well logging and formation evaluation[J].Engineering Science,5(9):87-85(in Chinese with English abstract)

Yan Chang-you,Yang Qi-xun,Liu Wang-shun.2005.A real-time data compression&reconstruction method based on lifting scheme[J].Proc CSEE,25(9):6-11(in Chinese with English abstract)

Yan Jia-bin,Liu Gui-zhong,Liu Jian-xin.2008.Application of wavelet transform in processing nature electromagnetic field time series[J].Geology and Exploration,44(3): 75-78(in Chinese with English abstract)

[附中文参考文献]

蔡剑华,汤井田,胡惟文.2010.基于经验模态分解的核磁共振测井信号去噪新方法[J].核电子学与探测技术,30(3):389-393

蔡剑华,王先春,胡惟文.2013.基于经验模态分解与小波阈值的MT信号去噪方法[J].石油地球物理勘探,48(2):303-3070

陈涛,李兵海.2008.基于小波变换去除遥感图像非高斯条纹噪音方法探讨[J].地质与勘探,1:19-27

沈路,周晓军,刘莉.2010.形态小波降噪方法在齿轮故障特征提取中的应用[J].农业机械学报,41(4):217-221

翁爱华,李舟波,莫修文.2003.低信噪比核磁共振测井资料的处理技术[J].吉林大学学报(地球科学版)，33(2):232-235

吴磊,孔力,程晶晶.2011.基于小波变换的核磁共振测井信号去噪算法设计[J].仪表技术与传感器,10:71-73

肖立志,谢然红.2003.核磁共振在石油测井与地层油气评价中的应用[J].中国工程科学,5(9): 87-85

闫常友,杨奇逊,刘万顺.2005.基于提升格式的实时数据压缩和重构算法[J].中国电机工程学报,25(9):6-11

严家斌,刘贵忠,柳建新.2008.小波变换在天然电磁场信号时间序列处理中的应用[J].地质与勘探,44(3): 75-78

De-noising of NMR Logging Signals Based on the Morphological Wavelet and its Real Application

CAI Jian-hua,LI Xiao-qin，ZHANG Xun

(InformationInstitute,HunanUniversityofArtsandScience,Changde,Hunan415000)

In nuclear magnetic resonance (NMR) logging,the echo signal is very weak while the background noise is strong.Thus it is difficult to separate signal and noise in the data.To solve this problem,this work combined mathematical morphology and multi-resolution analysis of wavelet decomposition to generate a new de-noising method for NMR logging signals,called the morphological wavelet.This paper presents its principle and operation steps,and compares its de-noising effect with that of the wavelet soft-threshold method.The processing results of real logging data show that this new method can preserve details and resist against noise well,superior to the wavelet soft-threshold method.When it removes random noise,the signal waveforms and characteristics can be retained.Even in the case of lowSNR,the useful information also can be effectively extracted,which enhances the inversion precision of the T2spectrum.

Morphological Wavelet,NMR Logging,Wavelet soft-threshold,de-noising