煤粉颗粒热解时的膨胀与其物理化学性质的关系

张盛诚， 何 榕

(清华大学 热能工程系， 北京 100084)



煤粉颗粒热解时的膨胀与其物理化学性质的关系

张盛诚， 何 榕

(清华大学 热能工程系， 北京 100084)

通过建立数学模型来研究煤粉颗粒热解时的膨胀规律，用分形孔隙模型生成煤粉的孔隙结构，描述热解过程发生的化学反应、气体在孔隙中的扩散和煤粉颗粒的膨胀与收缩.对模型计算结果进行拟合，得到描述煤粉颗粒膨胀的微分方程，通过与其他研究者模型计算结果的对比验证该微分方程，分析了煤种的官能团含量、煤粉颗粒的孔隙率和比表面积对其膨胀的影响，并定义了一个综合了煤的物理化学性质的参数X.结果表明：官能团含量上升，煤粉颗粒的最大膨胀率和煤焦的膨胀率增大；孔隙率或比表面积增大，煤粉颗粒的最大膨胀率和煤焦的膨胀率减小；参数X越大，煤粉颗粒在热解过程中会发生更大的膨胀.

煤； 热解； 官能团； 孔隙； 膨胀

热解是煤燃烧、气化和液化等过程的初始阶段，对后续过程有重要影响，很多学者对此进行了研究[1-3].随着温度的上升，煤粉颗粒在热解时会发生化学反应，释放挥发分[4].同时，煤是一种有机大分子，在高温下软化熔融，因此热解时煤粉颗粒也会发生膨胀和收缩.煤粉颗粒的膨胀和收缩直接影响热解过程中颗粒的大小，那么挥发分在颗粒中的停留时间也受到影响，进而影响挥发分在颗粒内部的二次反应，这会对热解产物的生成速率和产量有影响[5].热解时煤粉颗粒的膨胀和收缩也会影响热解结束时煤焦的物理结构和煤焦颗粒的反应活性[6].

Khan等[7]对24种不同的煤进行了实验，结果表明所采用的24种煤在热解过程中都有不同程度的膨胀和收缩.Yu等[8]研究了加热速率对3种煤粉颗粒膨胀的影响，结果表明随着加热速率的提高，最终获得的煤焦的膨胀率先增大，达到一个最大值之后进一步提高加热速率，煤焦的膨胀率却减小，这与Gale等[9]的实验结论一致.同时，Yu等[8]的研究也表明，对于同一种煤，粒径小的颗粒会发生更大的膨胀，这是因为镜质组在小颗粒中聚集，而镜质组是煤粉颗粒塑性的来源.Gale等[9]的研究表明，随着温度的上升，煤焦的膨胀率减小.Strezov等[10]使用CCD相机观察了煤粉颗粒膨胀率的实时变化，研究了压力对膨胀率的影响，结果表明热解时煤粉颗粒先发生膨胀随后发生收缩，随着压力的上升，煤粉颗粒的最大膨胀率和煤焦的膨胀率均先增大后减小，其原因是压力对煤粉颗粒的塑性有2方面的竞争性作用.还有一些研究者通过建立模型来研究煤粉颗粒热解时的膨胀和收缩规律.Melia等[11]基于孤立孔模型，对煤粉颗粒的膨胀进行了数值研究.Solomon等[12]基于FG-DVC模型建立了热解时煤粉颗粒的膨胀模型，应用该模型研究了压力对煤焦膨胀率的影响，结果表明随着压力的上升，煤焦的膨胀率先增大后减小，这与实验结果相吻合.Yu等[13]采用一个多孔气泡颗粒来描述煤粉的孔隙结构，建立描述煤粉颗粒膨胀的模型，并利用该模型预测煤粉颗粒的膨胀和收缩.但是，随着加热速率的上升，这些模型预测到的煤焦膨胀率是持续增大的，没有出现减小的现象，其原因是这些模型不适用于较大范围的加热速率.因此，这些模型没有基于准确的孔隙结构模型，不能用来研究原煤的孔隙结构对煤粉颗粒膨胀的影响.

然而，煤粉颗粒是一种典型的多孔介质，除了热解时的外界条件，煤粉本身的孔隙结构对煤粉颗粒的膨胀和收缩也存在影响，但由于目前的实验条件很难研究这一点，而且又缺少这方面的模型，因此关于这方面的研究很少.笔者基于分形孔隙模型建立了描述热解时煤粉颗粒膨胀和收缩的数学模型，利用该模型研究了煤中官能团含量、温度和孔隙结构对膨胀率变化速率的影响，得到了描述膨胀率变化速率的微分方程.煤粉颗粒的膨胀和收缩是由其物理化学性质决定的，利用该微分方程分别研究了煤的物理化学性质对煤粉颗粒膨胀的影响.

1 煤粉颗粒膨胀模型

1.1 模型的建立

煤粉颗粒具有发达而复杂的孔隙结构，采用Liang等[14]的分形孔隙模型生成孔隙结构来模拟真实的煤粉颗粒.通过分形孔隙模型生成的孔隙结构在孔隙率和比表面积上接近真实的煤粉颗粒，并且调整分形孔隙模型的输入参数可以生成具有不同孔隙率和比表面积的孔隙结构.图1给出了真实煤粉颗粒的SEM图和分形孔隙模型生成的孔隙结构，后者由100×100×100个立方体网格组成，分为气体网格(图1(b)中的白色网格)和固体网格(图1(b)中的黑色网格).其中，孔隙由气体网格组成，而煤分子和灰分则随机分布在固体网格中.

(a)煤粉颗粒的SEM图(b)孔隙结构

图1 煤粉颗粒的SEM图和孔隙结构

Fig.1 SEM images and pore structure of coal particles

热解时，固体网格中的煤分子发生化学反应，释放挥发分.化学反应采用Chen等[15]的FD(Fragmentation and Diffusion)煤热解模型来描述，该模型包含了热解时煤分子裂解、一次产物生成和二次反应，如图2所示.该模型假设煤分子由2 500个单体通过共价键连接形成大分子网络结构，每个单体由芳香簇和官能团组成，单体包含16种官能团，每种官能团可以裂解生成轻质气体，如生成CO2的羧基和生成H2O的羟基等.热解反应发生时，连接单体的共价键随机断裂形成焦油碎片和气体碎片.焦油碎片继续反应生成一次焦油，一次焦油在颗粒内部会发生二次反应，即交联反应和裂解反应.气体碎片中的官能团裂解生成轻质气体，芳香簇形成一次焦炭.

热解产生的气体分布在颗粒的内外表面上，通过孔隙向颗粒外部扩散.分形孔隙模型生成的孔隙结构中孔隙由一个个立方体网格组成，采用分子运动论来描述气体在网格中的扩散，这种方法已被Cao等[16]证实可以用来描述分形孔隙模型中气体的扩散.

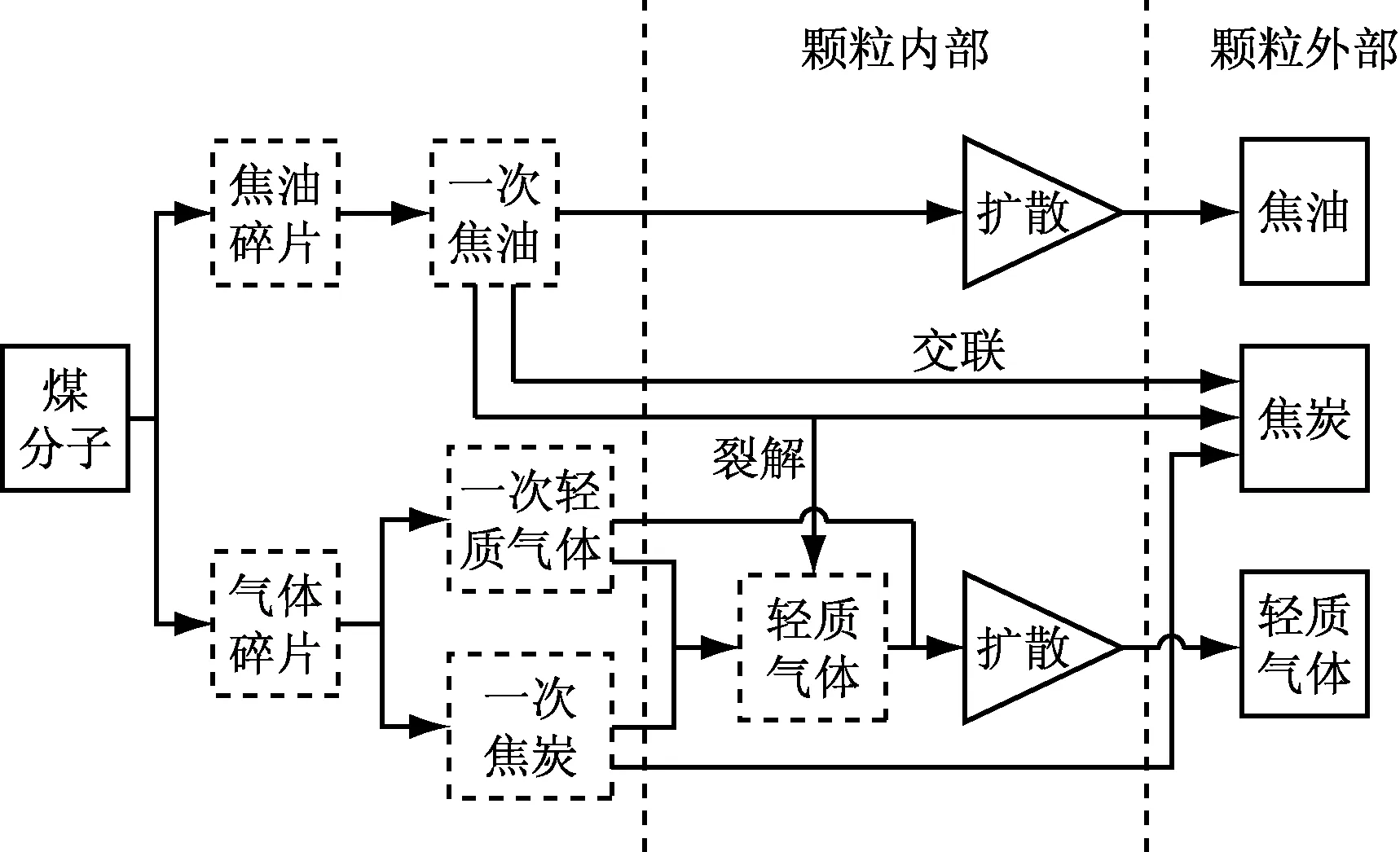
图2 FD煤热解模型

孔隙中聚集的气体使得颗粒内部压力上升，颗粒内外形成压力差，导致软化的煤粉发生膨胀[12]，膨胀引起的网格移动量采用以下公式[11]计算：

(1)

式中：Δl为固体网格的移动量；l为固体网格的长度；Δp为网格两端压力差；Δt为时间间隔；μ为煤粉颗粒的黏度.

采用Oh等[17]的经验公式来计算μ和T′：

(2)

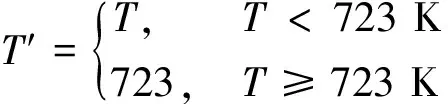
(3)

式中：φ′为胶质体的含量；T和T′为温度；E为参数，数值取自文献[17]；R为通用气体常数.

在热解后期，煤粉颗粒的黏度急剧增大，颗粒发生再固化和收缩.不同研究者对收缩临界黏度所取的值不同[18]，本文取为1.0×104Pa·s.软化熔融的煤粉颗粒表现出表面张力，由于分形孔隙模型生成的孔隙结构为立方体，可以假设为一个等效的压力作用在颗粒的外表面：

(4)

式中：σ为表面张力，σ=0.03 N/m[18]；r为颗粒的等效直径，m.

该等效压力计入式(1)的压力差Δp中，由式(1)计算表面张力引起的煤粉颗粒收缩.同时，热解时由于轻质组分的释放，煤粉真密度增大，导致颗粒收缩.Gale等[19]的研究表明，煤粉真密度仅与失重率有关，而与加热速率和热解温度等因素无关，据此可以得到真密度与失重率的关联式：

(5)

式中：ρt为煤粉的真密度；ρt0为原煤的真密度；x′为热解时煤粉的失重率.

真密度增大引起煤粉颗粒收缩，其体积变化为

(6)

式中：Vs为固体部分的体积：mp为颗粒的质量.

1.2 膨胀率变化速率

不同的煤种往往具有不同的官能团含量，而且官能团含量在热解过程中也是不断下降的，不同煤粉颗粒的孔隙率和比表面积也不同.煤粉颗粒的膨胀是由气体压力差导致的，官能团是气体的来源，其含量影响产气量，温度影响气体的生成速率，孔隙率和比表面积影响气体的分布，这4个参数都会影响颗粒内外的压力差，因此都对膨胀率的变化速率有影响.为了使模型的结果有较为普遍的适应性，通过对模型计算结果进行拟合，得到描述膨胀率变化速率的微分方程：

(7)

式中：α为膨胀率，为热解时煤粉的粒径与初始粒径之比；φ为官能团含量；θ为孔隙率；s为比表面积.

为了突出本文的研究重点，假设煤粉颗粒等温，忽略颗粒内部温度梯度，所有的模拟都在101 325 Pa下进行.FD煤热解模型假设煤分子中存在16种官能团，若考虑每一种官能团的影响将使式(7)异常复杂.为简化起见，忽略每一种官能团的影响，φ为16种官能团的总含量.从最后结果来看，这种简化是合理的.利用煤粉颗粒膨胀模型，给定初始的φ、T、θ和s，模拟一个较短时间的热解过程，用膨胀率变化量除以时间就可以得到该条件下的膨胀率变化速率.研究官能团含量的影响时，计算了12个算例，这些算例的初始温度设为1 100 K，初始孔隙率为0.32，比表面积为0.83×107m2/m3，而初始官能团含量则在0～0.53内变化.图3给出了官能团含量对膨胀率变化速率的影响，图中的每一个点为给定初始条件下一个算例计算出来的膨胀率变化速率，实线为曲线拟合的结果.从图3可以看出，当官能团含量高于0.111时，膨胀率变化速率为正，膨胀率增大，颗粒膨胀；当官能团含量下降到0.111时，煤粉颗粒黏度达到临界黏度1.0×104Pa·s时，膨胀率变化速率为0；当官能团含量低于0.111之后，膨胀率变化速率为负，膨胀率减小，颗粒收缩.采用同样的方法研究温度、孔隙率和比表面积对膨胀率变化速率的影响，然后采用曲线拟合得到这些自变量与膨胀率变化速率的关系.

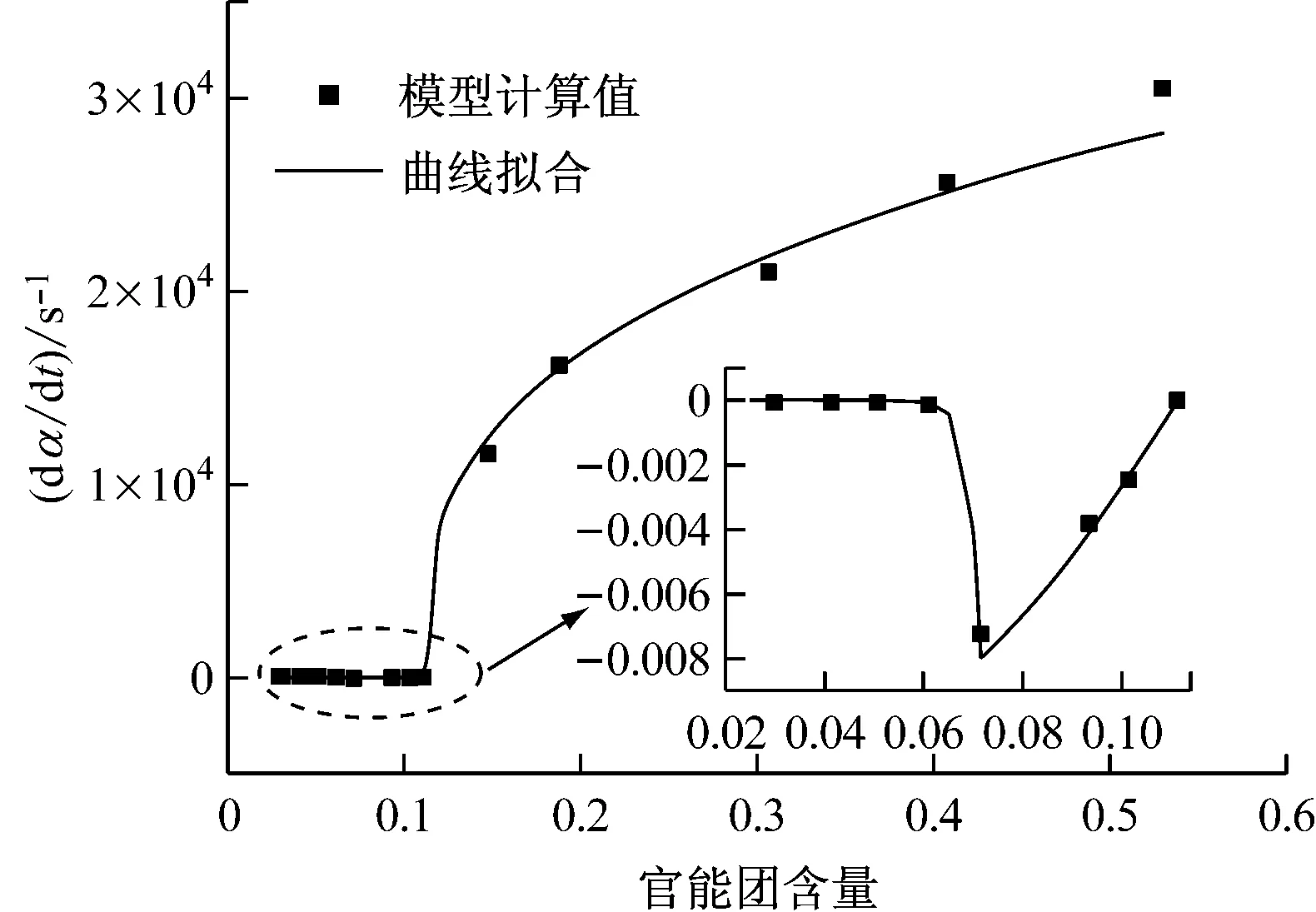
图3 官能团含量对膨胀率变化速率的影响

分别获得膨胀率变化速率与4个自变量之间的数学关系后，对所有算例的计算结果进行拟合，同时将膨胀率变化速率与4个自变量进行关联，可以得到描述膨胀率变化速率的微分方程：

(8)

(9)

(10)

1.3 微分方程的验证

为验证微分方程(8)的正确性，将采用该方程预测得到的膨胀率与其他研究者模型预测得到的膨胀率进行对比.笔者对4种煤热解过程中的膨胀率进行了预测，4种煤在沉降炉中通过对流和辐射加热，沉降炉壁温和气流温度均为1 473 K.4种煤的工业分析、官能团含量和初始孔隙参数见表1和表2.煤粉颗粒的初始粒径为30 μm.

图4给出了本文预测和其他研究者模型预测得到的膨胀率.从图4可以看出，Sheng等[18]的模型预测到了煤粉颗粒在热解时发生的膨胀，Yu等[13]的模型预测到了热解时煤粉颗粒先膨胀后收缩，本文的微分方程预测到了4种煤的膨胀和收缩.虽然不同研究者采用的煤种和加热速率等条件都不尽相同，但是通过对比图4，可以定性地证明本文得到的微分方程可预测热解时煤粉颗粒发生的膨胀和收缩. 从图4还可以看出，由于煤粉颗粒先膨胀后收缩，所以在热解过程中，煤粉颗粒在膨胀阶段结束时会出现最大膨胀率αm；在收缩阶段结束时，煤粉颗粒会达到最终膨胀率αc，最终膨胀率也是煤焦的膨胀率.

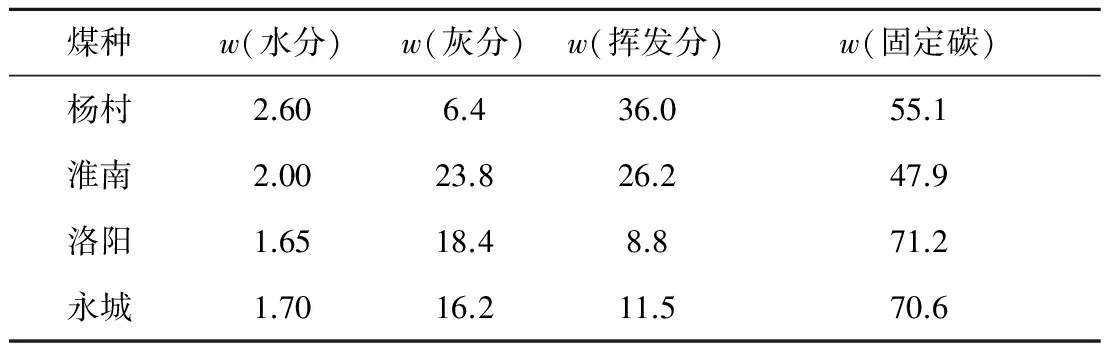
表1 4种煤的工业分析

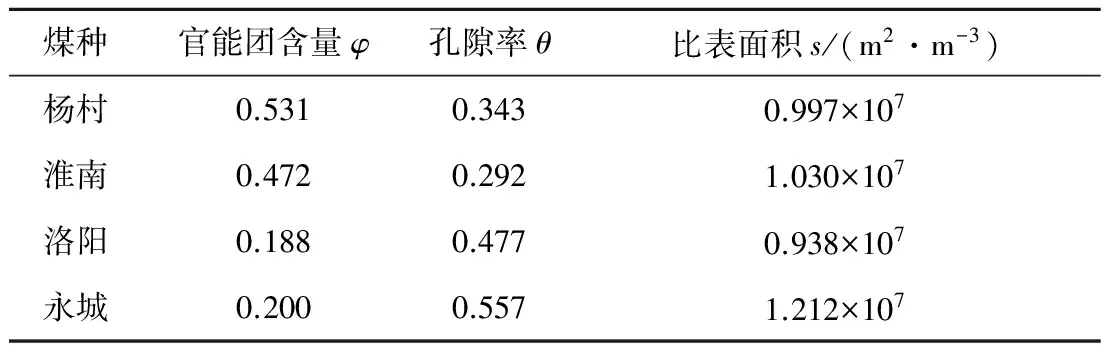
表2 4种煤的官能团含量和孔隙参数

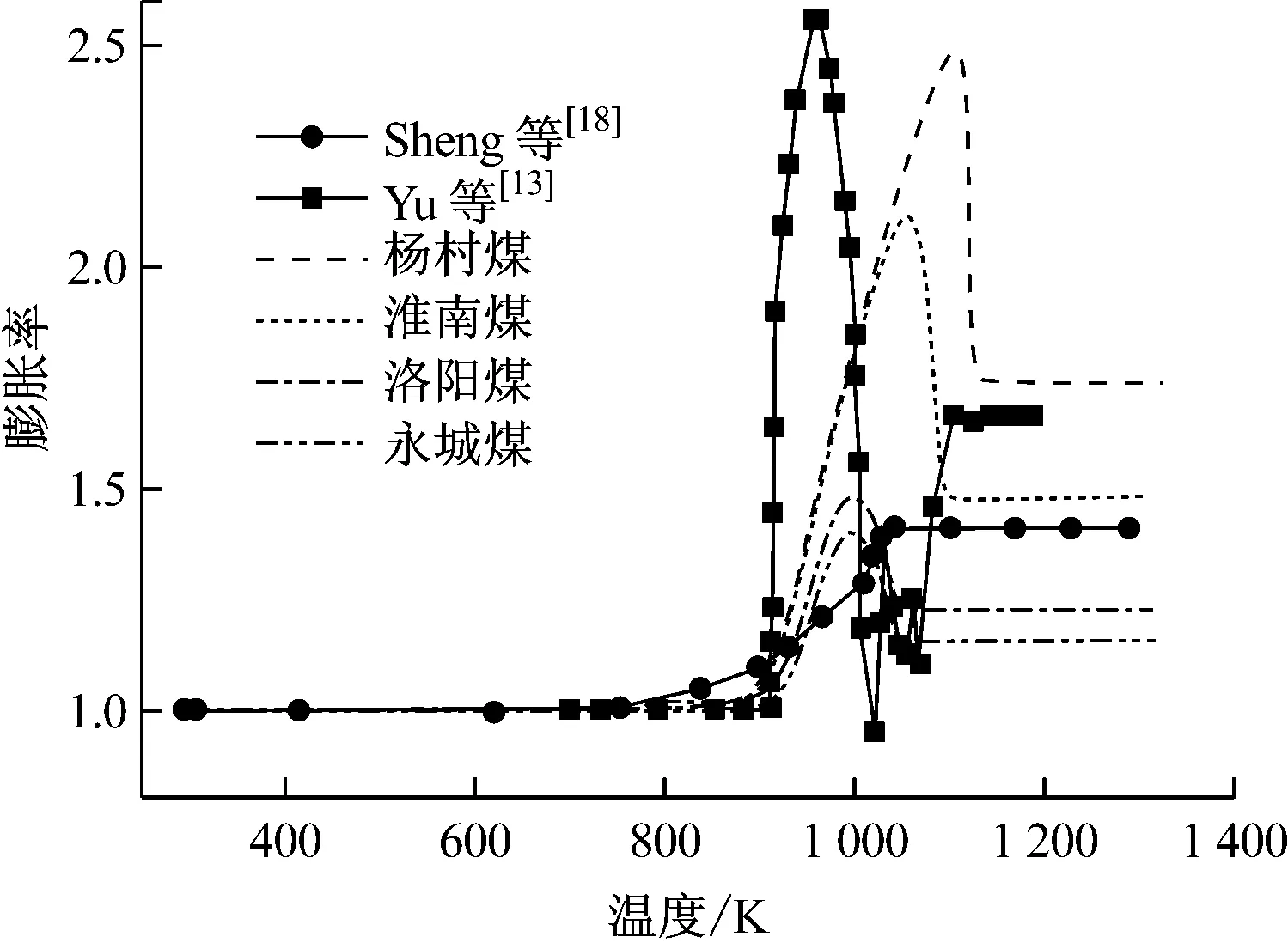
图4 热解时预测得到的膨胀率随时间的变化

2 膨胀率的变化

2.1 官能团含量的影响

研究官能团含量的影响时，初始孔隙率设为0.4，比表面积为1.0×107m2/m3，加热速率为3 000 K/s，当温度达到1 273 K之后保持温度不变，初始粒径为30 μm.图5给出了热解时煤粉颗粒最大膨胀率和煤焦膨胀率与原煤官能团含量的关系.从图5可以看出，随着官能团含量的上升，最大膨胀率增大.由于官能团是热解时气体的来源[20]，官能团含量越高，产气量也越高，因而导致颗粒内外形成更大的压力差，引起煤粉颗粒发生更大的膨胀.同时也可以发现最大膨胀率增大的趋势在减缓，这是由于在热解过程中，高官能团含量的煤粉颗粒发生的膨胀更大，煤粉颗粒的孔隙率和比表面积也更大，较大的孔隙率和比表面积有利于气体产物在孔隙中的扩散，从而减小颗粒内外压力差，使煤粉颗粒的膨胀变缓.从微分方程(8)也可以直接看出，在膨胀阶段，孔隙率和比表面积越大，膨胀率的变化速率越小.从图5还可以看出，煤焦膨胀率随着官能团含量的上升而增大.煤焦膨胀率是由热解时膨胀阶段和收缩阶段共同决定的.随着官能团含量上升，煤焦膨胀率增大是由于煤粉颗粒在膨胀阶段发生了更大的膨胀.煤焦膨胀率增大的趋势也在减缓，但是减缓的幅度比最大膨胀率的减缓幅度大，这是由于高官能团含量的煤粉颗粒发生了更大的收缩.官能团含量越高，一方面产气量越高，失重率越大，真密度增大越大，收缩加大；另一方面热解反应持续时间越长，而加热速率是一定的，导致煤粉颗粒会在更高的温度下收缩，而高温会加速煤粉颗粒的收缩，如微分方程(8)所示.

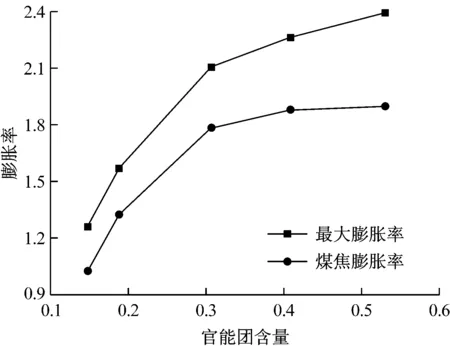
图5 官能团含量对最大膨胀率和煤焦膨胀率的影响

2.2 孔隙率的影响

研究孔隙率的影响时，原煤官能团含量为0.53，初始比表面积为1.0×107m2/m3，加热速率为3 000 K/s，当温度达到1 273 K之后保持温度不变，初始粒径为30 μm.图6给出了原煤孔隙率对最大膨胀率和煤焦膨胀率的影响.从图6可以看出，随着孔隙率的增大，最大膨胀率和煤焦膨胀率均减小.孔隙率越大，则煤焦颗粒中包含的有机煤分子越少，颗粒产气量越小，同时大的孔隙率有利于气体的扩散，这2个因素共同导致颗粒内外的压力差减小，从而引起的煤粉颗粒膨胀减小.最大膨胀率和煤焦膨胀率表现出的变化规律基本一致，这说明初始孔隙率对煤粉颗粒收缩的影响不大.微分方程(8)表明，在收缩阶段(官能团含量低于0.111)时，膨胀率变化速率与孔隙率无关.本文模型中颗粒的收缩是由于表面张力和真密度增大引起的，孔隙率对这2个因素都没有影响.

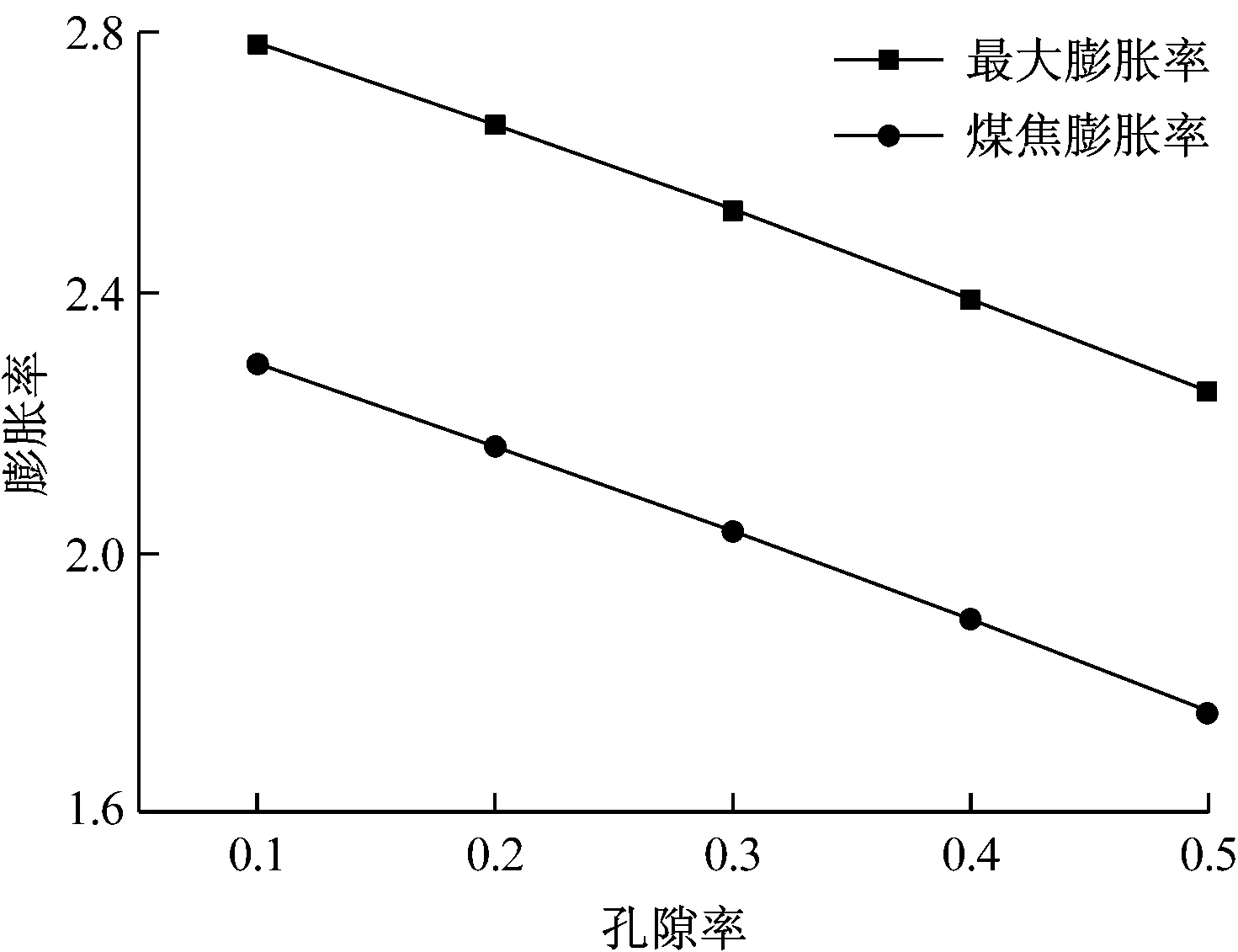
图6 孔隙率对最大膨胀率和煤焦膨胀率的影响

2.3 比表面积的影响

研究比表面积的影响时，原煤官能团含量为0.53，初始孔隙率为0.4，加热速率为3 000 K/s，当温度达到1 273 K之后保持温度不变，初始粒径为30 μm.图7给出了最大膨胀率和煤焦膨胀率与原煤比表面积的关系.从图7可以看出，随着比表面积的增大，最大膨胀率和煤焦膨胀率均减小.这是由于热解产生的气体分布在煤粉颗粒的表面上，比表面积越大，则气体分布在更大的表面上，导致压力减小，那么引起的煤粉颗粒膨胀也减小.最大膨胀率和煤焦膨胀率表现出的变化规律基本一致，这是因为和孔隙率一样，比表面积对煤粉颗粒收缩的影响不大.比较图5～图7可以发现，相对官能团含量和孔隙率，比表面积对膨胀率的影响要小一些.

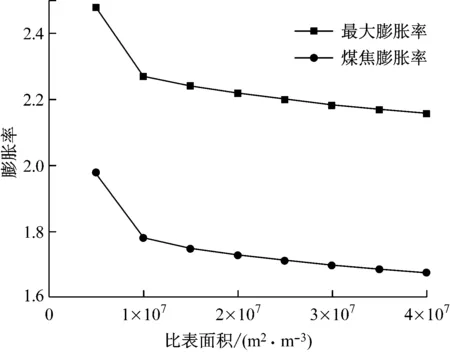
图7 比表面积对最大膨胀率和煤焦膨胀率的影响

3 分析与讨论

官能团含量表征了煤的化学性质，而孔隙率和比表面积则表征了煤的物理性质.在外界条件(加热速率、热解终温等)保持不变的情况下，煤粉颗粒的膨胀是由其物理化学性质共同决定的，膨胀也体现了其物理化学性质.由于热解过程中煤粉颗粒的膨胀是由颗粒内外压力差引起的，所以影响颗粒内部压力形成的因素都会对膨胀产生影响.其中，官能团及其含量影响颗粒内部的压力；而孔隙率和比表面积则决定生成气体的分布和扩散，会影响颗粒内外的压力差.定义一个表征煤的物理化学性质的综合参数X来研究煤粉颗粒膨胀与煤本身性质的关系：

(11)

(12)

式中：sr为相对比表面积.

参数X是无量纲的，将参数X定义成式(11)的形式是考虑到官能团含量上升会增大煤粉颗粒的膨胀，孔隙率和比表面积增大则减小煤粉颗粒的膨胀，而且相比于官能团含量和孔隙率，比表面积对膨胀的影响要小.

图8给出了参数X与最大膨胀率和煤焦膨胀率的关系，其中横坐标为1/X，纵坐标为lnα.从图8可以看出，最大膨胀率的对数值lnαm和煤焦膨胀率的对数值lnαc都与1/X具有很好的线性关系，相关系数分别为0.991和0.973.通过线性回归还可以发现，最大膨胀率对数值拟合直线的斜率为-0.307，而煤焦膨胀率对数值拟合直线的斜率为-0.295，取绝对值之后，前者略大，这说明参数X对最大膨胀率的影响要大于对煤焦膨胀率的影响，这就印证了图5中的现象.图5表明，官能团含量上升，虽然最大膨胀率和煤焦膨胀率的曲线都变得平缓，但是煤焦膨胀率的曲线更平缓一些，说明煤焦膨胀率受到的影响更小.通过拟合得到最大膨胀率和煤焦膨胀率与参数X的关系为

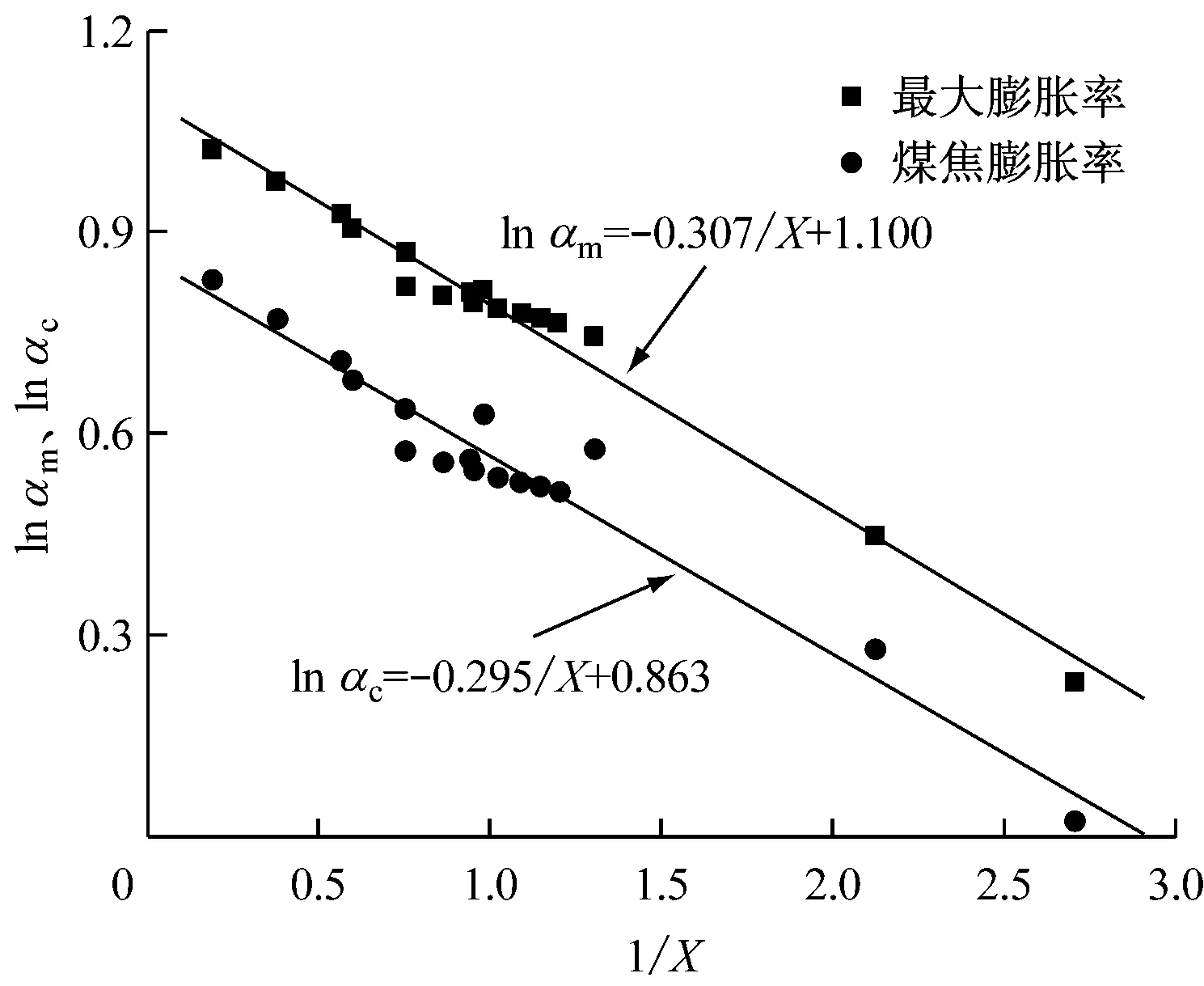
图8 参数X与最大膨胀率和煤焦膨胀率的关系

(13)

(14)

参数X实际上反映了煤粉颗粒本身的膨胀能力，综合考虑了物理化学性质对膨胀的影响.参数X越大，不论是由于官能团含量越高还是由于孔隙率或比表面积越小，热解过程中颗粒内外形成的压力差都会越大，那么煤粉颗粒的膨胀也会越大.由式(13)和式(14)可知，最大膨胀率和煤焦膨胀率与1/X呈现出负的指数关系，表明虽然随着参数X的增大，煤粉颗粒的最大膨胀率和煤焦膨胀率增大，但是增大的幅度在减缓.这是因为煤粉颗粒膨胀得越大，煤粉颗粒的孔隙率和比表面积增大得越多，这有利于颗粒内部压力的释放，从而减缓煤粉颗粒的膨胀.

4 结 论

(1) 煤粉颗粒的最大膨胀率和煤焦膨胀率随着官能团含量的上升而增大，随着孔隙率或比表面积的增大而减小.

(2) 在外界条件一定时，煤粉颗粒的膨胀只与煤本身的物理化学性质有关，所定义的参数X反映了煤粉颗粒本身的膨胀能力.

(3) 随着参数X的增大，热解过程中煤粉颗粒的最大膨胀率和煤焦膨胀率均增大，但是增大的幅度在减缓.

[1] 李乾坤, 周劲松, 骆仲泱, 等. 煤种及热解条件对煤焦脱除烟气汞的影响[J]. 动力工程学报, 2012, 32(6): 463-468.

LI Qiankun, ZHOU Jinsong, LUO Zhongyang,etal. Effect of coal type and pyrolysis condition on removal efficiency of flue gas mercury by coal char[J]. Journal of Chinese Society of Power Engineering, 2012, 32(6): 463-468.

[2] 夏芝香, 岑建孟, 唐巍, 等. 热解温度对2种煤在流化床中热解产物的影响[J]. 动力工程学报, 2015, 35(10): 792-797, 839.

XIA Zhixiang, CEN Jianmeng, TANG Wei,etal. Effects of pyrolysis temperature on pyrolysis products of two kinds of coal in a fluidized-bed reactor[J]. Journal of Chinese Society of Power Engineering, 2015, 35(10): 792-797, 839.

[3] 虞君武, 陈永利, 何榕, 等. FD模型应用于煤热解过程的数值模拟[J]. 化工学报, 2014, 65(9): 3592-3598.

YU Junwu, CHEN Yongli, HE Rong,etal. Numerical simulation of coal pyrolysis using FD model[J]. CIESC Journal, 2014, 65(9): 3592-3598.

[4] SOLOMON P R, SERIO M A, SUUBERG E M. Coal pyrolysis: experiments, kinetic rates and mechanisms[J]. Progress in Energy and Combustion Science, 1992, 18(2): 133-220.

[5] SIMONS G A. Coal pyrolysis II. species transport theory[J]. Combustion and Flame, 1984, 55(2): 181-194.

[6] HE Rong, SATO J I, CHEN Changhe. Modeling char combustion with fractal pore effects[J]. Combustion Science and Technology, 2002, 174(4): 19-37.

[7] KHAN M R, JENKINS R G. Swelling and plastic properties of coal devolatilized at elevated pressures: an examination of the influences of coal type[J]. Fuel, 1986, 65(5): 725-731.

[8] YU Dunxi, XU Minghou, YU Yun,etal. Swelling behavior of a Chinese bituminous coal at different pyrolysis temperatures[J]. Energy & Fuels, 2005, 19(6): 2488-2494.

[9] GALE T K, BARTHOLOMEW C H, FLETCHER T H. Decreases in the swelling and porosity of bituminous coals during devolatilization at high heating rates[J]. Combustion and Flame, 1995, 100(1/2): 94-100.

[10] STREZOV V, LUCAS J A, WALL T F. Effect of pressure on the swelling of density separated coal particles[J]. Fuel, 2005, 84(10): 1238-1245.

[11] MELIA P F, BOWMAN C T. A three zone model for coal particle swelling[J]. Combustion Science and Technology, 1983, 31(3/4): 195-201.

[12] SOLOMON P R, SERIO M A, HAMBLEN D G,etal. Measurement and modeling of advanced coal conversion processes[R]. Washington D C, USA: USDOE, 1992.

[13] YU Jianglong, LUCAS J, WALL T F,etal. Modeling the development of char structure during the rapid heating of pulverized coal[J]. Combustion and Flame, 2004, 136(4): 519-532.

[14] LIANG Zhanggang, HE Rong, CHEN Qun,etal. Fractal generation of char pores through random walk[J]. Combustion Science and Technology, 2007, 179(3): 637-661.

[15] CHEN Yongli, HE Rong. Fragmentation and diffusion model for coal pyrolysis[J]. Journal of Analytical and Applied Pyrolysis, 2011, 90(1): 72-79.

[16] CAO Liyong, HE Rong. Gas diffusion in fractal porous media[J]. Combustion Science and Technology, 2010, 182(7): 822-841.

[17] OH M S, PETERS W A, HOWARD J B. An experimental and modeling study of softening coal pyrolysis[J]. AIChE Journal, 1989, 35(5): 775-792.

[18] SHENG Changdong, AZEVEDO J L T. Modeling the evolution of particle morphology during coal devolatilization[J]. Proceedings of the Combustion Institute, 2000, 28(2): 2225-2232.

[19] GALE T K, FLETCHER T H, BARTHOLOMEW C H. Effects of pyrolysis conditions on internal surface areas and densities of coal chars prepared at high heating rates in reactive and nonreactive atmospheres[J]. Energy & Fuels, 1995, 9(3): 513-524.

[20] GAVALAS G R, CHEONG P H K, JAIN R. Model of coal pyrolysis. 1. qualitative development[J]. Industrial & Engineering Chemistry Fundamentals, 1981, 20(2): 113-122.

Relationship Between Swelling Behavior and Physical/Chemical Properties of Coal Particles During Pyrolysis

ZHANG Shengcheng, HE Rong

(Department of Thermal Engineering, Tsinghua University, Beijing 100084, China)

To investigate the coal particle swelling behavior during pyrolysis, a numerical model was developed by using the fractal pore model to generate the coal particle pore structure, and then to describe the chemical reactions, gas diffusion and the swelling and contraction behavior of coal particles during pyrolysis. Based on fitted curves with model results, a differential equation was obtained to describe the coal particle swelling, which was validated by comparing with predicted results of other researchers, and was then used to study the effects of following factors on the swelling, such as the functional group content, particle porosity and specific surface, etc., and finally a comprehensive parameterXwas defined to characterize the swelling ability of coal particles in consideration of above factors. Results show that both the maximum coal particle swelling ratio and the char swelling ratio increase with rising functional group content, and with reducing porosity and specific surface area. The larger theXis, the greater the swelling of coal particles will be during pyrolysis.

coal; pyrolysis; functional group; pore; swelling

2016-01-04

2016-02-29

国家自然科学基金资助项目(51176096)

张盛诚(1988-)，男，湖北黄冈人，博士，研究方向为煤的热解. 电话(Tel.)：15800648491； E-mail：zsc19881218@163.com.

1674-7607(2016)12-0951-07

TQ530.2

A 学科分类号：470.10