一种基于多线程加密的防伪二维码的生成方法
2016-12-23郑志学李长云
郑志学,李长云,倪 伟
(湖南工业大学 计算机与通信学院,湖南 株洲 412007)
一种基于多线程加密的防伪二维码的生成方法
郑志学,李长云,倪 伟
(湖南工业大学 计算机与通信学院,湖南 株洲 412007)
针对运用RSA算法生成防伪二维码过程中,因大数的模幂运算导致效率低下的问题,利用GPU在多线程并行计算中的优势,将大数的模幂运算转化为小整数的多阶段的并行模幂运算,采用多线程技术对分解后的小数进行处理,最终合并运算结果,生成相应的防伪二维码。通过一系列实验对改进前后的二维码生成时间进行对比,结果表明改进后的方案能有效地提升防伪二维码系统的运行效率。
GPU;RSA加密;并行运算;二维码
0 引言
二维码是一种新兴的信息数据的载体,自20世纪80年代产生以来以其独特的便利特性得到了广泛的应用。随着科学技术和理论研究的不断发展,二维码的种类和表现形式呈现多态特性,其中比较流行的有PDF417、QR Code、Data Matrix、Maxi Code等[1]。而QR Code以其良好的兼容性和纠错性在支付和数据传输方面得到了更为广泛的关注和运用。在商业活动中对产品信息的保护非常重要,而QR Code的低成本、易生成和便携带的特点使其成为商业活动中的重要信息携带载体[2]。传统的二维码信息极易被仿造和复制,在一些较为重要商品信息的流通过程中此问题尤为突出。因此,针对二维码的防伪加密研究已经成为国内的研究热点,而基于RSA非对称加密技术的防伪二维码生成方式,以其密匙传输的便利特性和极高的安全性得到了广泛的应用[3]。然而随着计算机硬件的快速发展和加密技术的理论研究不断深入,对加密数据进行攻击和破解的技术也在快速地提升。因此,以大数分解难度作为其安全性保证的RSA加密算法,需不断地提升其密匙长度来适应不同环境下的安全要求。虽然大数分解作为数学界至今未解的难题,但是通过不断提升模长来保证数据信息的安全性则成为制约RSA加密算法应用的瓶颈。目前768 b模长的RSA体制已经不再安全,一般采用1 024 b或2 048 b的模长体制才能保证信息的安全性[4],但与此同时,增大模长体制的加密方式也使得产生密文的时间成倍增长,由此导致了防伪二维码的生成效率极为低下。
因此本文提出了一种基于多线程的防伪二维码生成方法,借助GPU在并行计算上的优势,将RSA加密算法中的极大整数进行分解,利用多线程的小整数模幂运算来缩短加密时间,达到提升防伪二维码生成效率的目的。
1 传统防伪二维码加密方式
由于非对称加密算法中产生了2种不同的密匙,即公匙和私匙,而私匙的保密性和公匙的可分发性使得非对称加密算法的应用范围极为广泛,而非对称加密算法中的RSA算法在经历了30多年发展和验证之后,其安全性和稳定性得到了广泛的认可。随着二维码技术的逐渐成熟和流行,在商业活动中运用二维码进行防伪的方法得到越来越广泛的关注,而RSA非对称的加密算法以其良好的安全性和稳定性逐渐成为二维码加密防伪的主要方式。
1.1 RSA加密算法原理描述
RSA加密算法是在1977年由美国麻省理工学院R. Rives、A. Shamir、L. Adleman 3位学者提出的[5]。经过多年的实践验证,RSA算法以其算法的完善性、安全性和便于实现等特性得到了广泛的应用[6]。其基本实现方法如下。
1)为了保证加密的可靠性,先随机获取2个极大的素数p和q。
2)通过公式n=pq和gcd(e, (n))=1计算出响应的函数值。
3)随机选取极大整数公匙e使其满足gcd(e, (n))= 1。
4)通过公式ed≡1(mod (n))来求解密匙L。
5)保留从上面获取公匙e,私匙d和模长n,以(e, n)作为加密公匙,以(d, n)作为加密私匙。
6)通过加密算法c=E(m)=me(mod n)和解密算法m=D(c)=cd(mod n)来对数据信息进行加密和解密操作。
大数分解依然是数论中一个未解的难题,因此破译RSA的难度几乎与大数的分解难度等价[7]。RSA加密算法作为目前最优秀也是应用最广泛的公匙方案,在过去的几十年中经历了各种破译考验而逐渐被人们所接受和认可[8]。RSA算法加密和解密的流程如图1所示[9]。
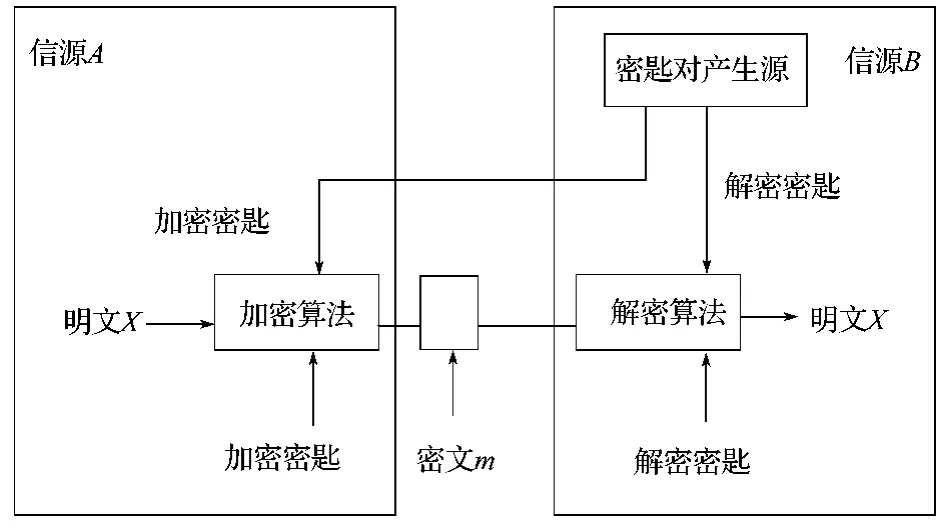
图1 RSA加密和解密流程图Fig. 1 Flow chart of RSA encryption and decryption
1.2 传统基于非对称加密的防伪二维码存在的问题
RSA算法的安全性建立在以大数分解困难的基础上,虽然大数分解的是数论中一个未解的难题,但是随着计算机硬件和密码学理论不断地发展,以RSA为代表的非对称加密算法的安全性不断地受到新的威胁。1994年彼得·秀尔证明一台量子计算机可以在多项式时间内进行因数分解。1999年,数百台电脑合作分解了一个512 b的密码,从而导致需要不断地增长密匙的长度。到目前为止公认较为安全的密匙长度为1 024 b,而在一些对安全要求极为严格的领域,密匙长度甚至达到2 048 b。随着密匙长度的不断增加,密匙产生的效率也在不断地下降,加密时间也在不断地增长,从而影响防伪二维码生成系统的整体效率。由此可知,如何缩短加密时间是提升防伪二维码生成系统的整体效率的关键所在。图2为不同密匙长度条件下加密大小分别为200 B,2 kB,10 kB数据的加密时间对比。
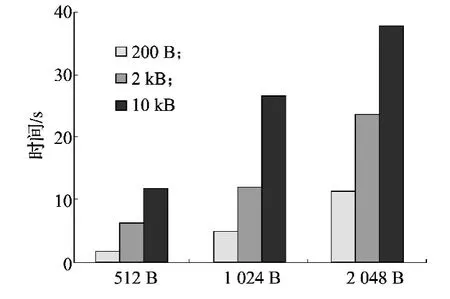
图2 不同密匙长度下数据加密时间Fig.2 Data Encryption Time under Different Key Lengths
2 GPU多线程并行运算技术
当前社会信息量呈现爆炸式增长,从而导致数据计算量不断提升,传统的基于CPU的串行计算方式已经无法满足人们对高效数据处理的要求,而GPU在多线程并行数据处理方面的先天优势则越来越受到广泛的关注。基于GPU的多线程并行运算的CUDA(compute unified device architecture)框架则是在这种需求条件下产生的,它以成本低廉、易于实现和无需掌握复杂的图像编程方法而逐渐被人们所认可。其架构的基本原理为:以CPU作为Host端来控制整体复杂的计算任务流程,以GPU作为Device端,利用其多核多线程的优势,根据Host端的任务调度进行高密度的并行数学计算,最终将计算结果反馈到Host端从而大大缩短数据计算的时间,为数据的后续操作提供了便利。通过CUDA框架实现多线程高并发的流程如图3所示。

图3 CUDA框架实现多线程高并发的流程Fig. 3 Flowchart of the multi-threading high concurrency achieved under CUDA framework
3 基于多进程的RSA加密算法生成防伪二维码方案
3.1 基本原理
传统防伪二维码的生成效率低下的原因在于:采用非对称的RSA算法进行加密操作时,为了保证信息的安全性故而采用了较长的密匙,而大数的模幂运算在串行方式情况下不仅效率低下而且对系统的资源要求也十分苛刻。因此假设需要加密的明文信息为某一大整数X,而X可以分解为多个小整数的乘积,即X=X1×X2×…×Xn,由此可知原本的计算密文的算法就改为Y=(X1×X2×…×Xn)e(mod n)。进一步可以转化为。从而将大数的模幂运算转换成小整数的运算,通过基于CUDA架构的多线程并行运算来提升加密的效率。
3.2 实现步骤
1)首先获取500以内的素数作为基本的小整数。
2)设需要加密的明文信息为一大整数X,根据因式分解的性质可知如果小素数a和b均为X的因子,那么素数a和b的乘积也必然是X的因子。因此,假设获取的素数个数为N,并行线程数为M则每一个线程中分配的因子个数S为N/M个,为了避免进程中的素数大小分配不均导致个别线程计算效率低下的问题,在分配素数之前需要先对基本N个小整数进行排序,按照两端各自取数的分配方式来使得素数能够平均分配在不同的线程中。
3)在各个线程中对所分配的基本小素进行整除运算,保留那些能够整除X的基本小数(以X1X2…Xn为例),对保留的小数就进行如下运算X=X/(X1× X2×…×Xn),之后重复步骤2,直至没有能够被整除的素数为止。
4)通过以上步骤保留的小整数即可作为多线程并行运算的最终小整数,按照步骤2中对基数排序的方式对小整数进行排序,再次将这些小整数平均地分配到不同的线程中,在不同的线程中计算不同的密文信息,如线程1中分配的小整数为X1X2…Xm,线程2中分配的小整数为Xm+1Xm+2…Xn,则根据密文的计算公式线程1中的最终整数即为,线程2的最终整数为,之后的线程以此类推从而最终的密文信息Y=Y1Y2…Yn(mod n)。
5)根据密文信息Y生成相对应的二维码。
整体流程如图4所示。
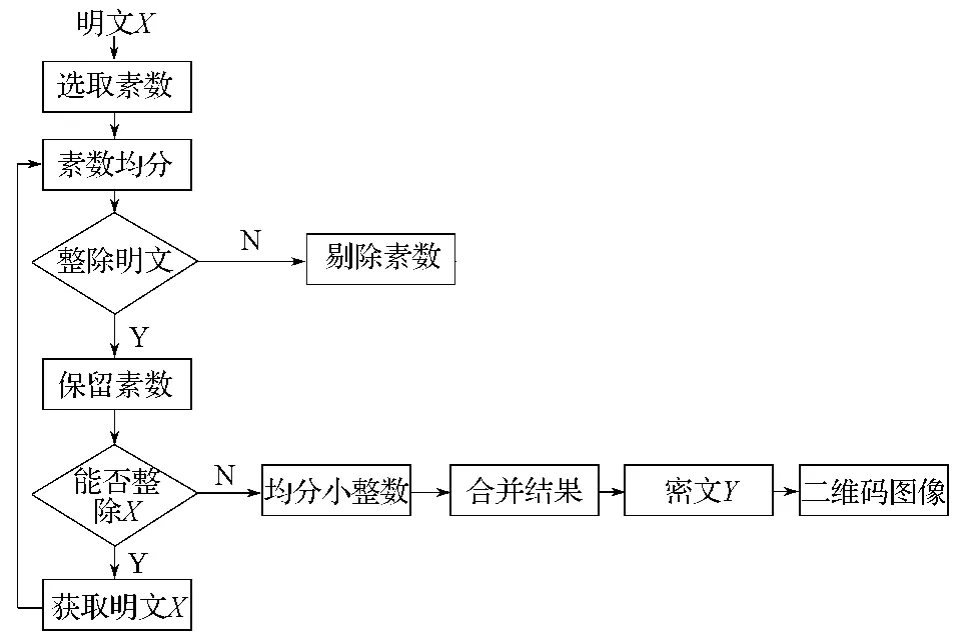
图4 多线程防伪二维码生成流程Fig. 4 Generation process of multi-threading counterfeit-proof two-dimensional codes
4 实验与结果分析
本文按照文中所述的实现方式,采用配置为Intel酷睿双核2.0 GHz,2 G内存,500 G硬盘,GT420M显卡为主要硬件平台,以Windows 7系统作为系统测试平台,以CUDA架构作为数据多线程并行加密的实现方式,以Visual Studio 6.0为开发工具,采用尺寸为256×256容错等级为L的二维码进行测试和验证。
当数据量较小时,采用多线程并行运算对单次的数据加密时间极短,从而无法统计较为准确的单次防伪二维码生成时间。考虑到实际情况下二维码的信息存储量限制,产品防伪数据大小一般不会超过500 B,因此本文采用数据量为100, 300, 500 B的明文信息分别在模数长度为512, 1 024, 2 048 b的条件下进行测试,将传统防伪二维码和改进后的二维码生成时间进行对比,实验统计如表1和表2所示。实验结果表明,在明文数据量相同的情况下,改进后的多线程并行产生防伪二维码的产生的时间比传统串行加密生成防伪二维码的时间缩短了近60%,而且当数据量增加时候,防伪二维码的产生效率也有明显的提升。以上结果说明,本文提出的基于多线程的并行加密方式生成二维码的方法,能有效地改进传统防伪二维码生成效率低下的问题。
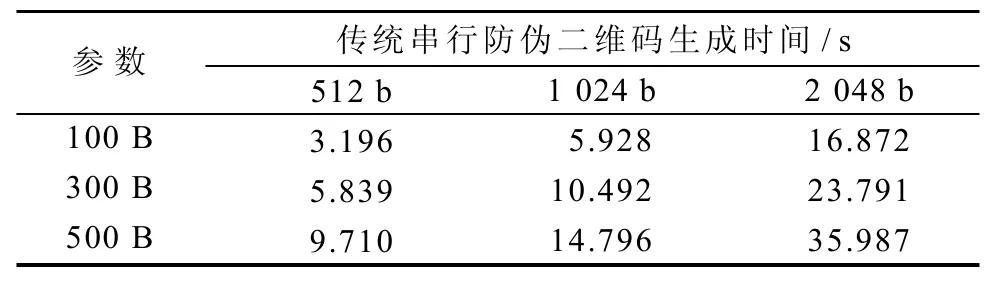
表1 传统防伪二维码生成时间Table 1 Generation time of conventional counterfeitproof two-dimensional codes

表2 改进后的防伪二维码生成时间Table 2 Generation time of improved counterfeitproof two-dimensional codes
5 结语
传统防伪二维码因为是基于CPU的串行加密方式,当数据量较大时,生成防伪二维码的时间大部分消耗在对明文数据处理的阶段,从而大大降低了整体二维码的生成效率。然而由于加密方式的不同,到目前为止还没有一个较为系统的提升防伪二维码生成效率的方案。因此本文在分析传统基于RSA加密的防伪二维码生成方式的基础上,借鉴并行运算对数据处理的高效特性,提出基于GPU的多线程并行加密运算生成防伪二维码的方法来改善防伪二维码的生成效率问题,提升系统整体稳定性。同时由于多线程并行运算中因数据分布不均从而影响系统的整体效率,以后将在多线程并行运算中线程数的选择以及小素数平均分配问题上作进一步的研究。
[1]于英政. QR二维码相关技术的研究[D]. 北京:北京交通大学,2014.YU Yingzheng. Research on QR Code Correlation Technique [D]. Beijing:Beijing Jiaotong University,2014.
[2]陈 君. 二维码技术在移动终端的安全应用研究[D]. 广州:广东工业大学,2015. CHEN Jun. QR-Code Technology in the Mobile Terminal Security Application Research[D]. Guangzhou:Guangdong University of Technology,2015.
[3]王立新. 基于移动物联网的溯源与防伪系统的设计与实现[D]. 成都:电子科技大学,2015. WANG Lixin. Design and Implementation of Traceability and Anti-Counterfeiting System Based on Mobile Internet of Things[D]. Chengdu:University of Electronic Science and Technology of China,2015.
[4] 胡 云. RSA算法研究与实现[D]. 北京:北京邮电大学,2010. HU Yun. Research and Implementation of RSA Algorithm [D]. Beijing:Beijing University of Posts and Telecommunications,2010.
[5] 张永建. RSA算法和SM2算法的研究[D]. 赣州:江西理工大学,2015. ZHANG Yongjian. Research on RSA Algorithm and SM2 Algorithm[D]. Ganzhou:Jiangxi University of Science and Technology,2015.
[6]YANG C C,CHANG T S,JEN C W. A New RSA Cryp,tosystem Hardware Design Based on Montgomerys Algorithm[J]. IEEE Trans Circuits and Systems,1998,45 (7) :908-913.
[7] 钱亚彬. 基于RSA算法的二维码防伪技术在生鲜产品领域的设计与应用[D]. 开封:河南大学,2015. QIAN Yabin. QR-code Anti-Counterfeiting Technology Based on RSA Algorithm Design and Application in the Field of Fresh Products[D]. Kaifeng:Henan University, 2015.
[8]宋 琦. 基于RSA的一般访问结构的秘密共享研究[D].合肥:合肥工业大学,2015. SONG Qi. General Access Structure Based on RSA Secret Sharing Research[D]. Hefei:Hefei University of Technology,2015.
[9]孙 伟. 公钥RSA加密算法的改进与实现[D]. 合肥:安徽大学,2014. SUN Wei. Improvement and Implementation of a Public Key RSA Encryption Algorithm[D]. Hefei:Anhui University,2014.
(责任编辑:申 剑)
A Generation Method of Counterfeit-Proof Two-Dimensional Codes Based on Multi-Threading Encryption
ZHENG Zhixue,LI Changyun,NI Wei
(School of Computer and Communication,Hunan University of Technology,Zhuzhou Hunan 412007,China)
In view of the inefficiency resulting from modular exponentiation of large numbers in the generation process of counterfeit-proof two-dimensional codes by using RSA algorithm, the modular exponentiation of large numbers can be transformed into the small integer stage parallel modular exponentiation by taking advantage of GPU in the multithreading parallel computing process. The fractional decimals can be processed by adopting the multi-threading technique, with the final calculation result merged together, to generate the corresponding counterfeit-proof two-dimensional code. A comparison has been made between the generation time of the two-dimensional codes before and after they are improved. The experimental results show that the improved scheme helps to improve the efficiency of the two-dimensional code system effectively.
GPU;RSA encryption;parallel arithmetic;two-dimensional codes
TP301.6
A
1673-9833(2016)05-0041-04
10.3969/j.issn.1673-9833.2016.05.009
2016-07-17
郑志学(1989-),男,河南济源人,湖南工业大学硕士生,主要研究方向为数据加密与防伪,E-mail:sunfree@qq.com
