机床多体系统空间刚度场约束下的加工误差预测

高羡明,洪军,甄宜超

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.西安精雕软件科技有限公司,710119,西安)



机床多体系统空间刚度场约束下的加工误差预测

高羡明1,洪军1,甄宜超2

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.西安精雕软件科技有限公司,710119,西安)

针对机床加工误差预测结果不连续的问题,提出了一种基于多体系统理论的机床加工空间连续误差预测方法。该方法结合多体系统运动学求解特点,将机床部件视作弹性体,利用低序体阵列和传递矩阵来描述机床部件之间的运动关系;基于刚度缩聚理论与最小二乘法原理,提取体单元移动载荷约束下的刚度缩聚模型;基于雅克比传递矩阵建立整机空间加工误差模型。结合切削工艺模拟方法,以某镗铣复合加工中心加工发动机壳体为例,对发动机壳体的立面、底面以及孔特征进行立铣、端铣、镗孔加工误差预测。基于复合工艺约束下的加工误差预测模型,对多种装夹角度下的发动机壳体加工误差进行了对比分析,结果表明,利用多体系统进行低序体阵列描述,有利于实现组合式加工误差求解,可用于机床的组合优化分析;结合切削工艺模拟的复合加工误差分析,以发动机壳体装夹角度为优化目标进行加工工艺优化设计,当转角为90°时,加工精度可提高35%。该方法能够有效地预测加工误差,进而支持机床的工艺优化设计。

数控机床;多体系统理论;误差预测;加工空间;工艺优化

现代机床制造技术正朝着高速度、高精度的方向快速发展,提高机床精度的研究也备受重视。机床通过刀具与工件之间的相对运动来完成零件表面的成形加工[1],而刀具和工件相对位置变化是通过改变机床各个部件相对位姿而实现的。机床部件相对位姿的变化造成了机床整机构型的改变,进而导致了机床刚度性能在机床加工空间内的不均匀性,从而不可避免地产生了机床加工误差。

为提高机床加工质量,降低误差,必须对影响机床加工误差的因素进行分析,建立空间加工误差模型。针对机床加工误差的预测问题,国内外学者做了大量的研究工作,其中文献[2]运用多体系统理论和齐次坐标系变换方法,考虑部件的运动学关系,建立了五轴数控机床加工S形检测试件的误差模型;文献[3]基于Proe模型,建立了机床加工空间误差预测模型;文献[4]以多轴磨床为对象,建立了误差预测模型;文献[5-9]采用多体系统理论建立了机床的误差模型。以上学者从多个角度对机床误差进行建模,误差预测模型目标是建立加工误差预测与影响因素的关联关系,然而大部分研究都将机床部件视作刚体,不考虑受载变形。对此文献[10]建立了多轴加工系统的刚度性能模型,分析了机床受载性能;文献[11-13]对影响机床性能的各项因素进行了研究分析;文献[14-15]基于多体系统运动学理论,建立了复杂装备的运动传递关系;文献[16]基于刚度组集理论对混联机床进行了静刚度分析与优化技术研究。以上研究工作考虑了影响机床受载变形的刚度指标,然而在空间变形分析方面以离散点变形分析为主,存在一定的不足。

结合多体系统运动求解的特点,将部件视为弹性体,通过刚度模型建立受载与变形的关联关系,从而实现了机床受载约束下的整机加工空间误差预测。本文提出了一种基于多体系统理论的机床加工空间误差预测方法,该方法具有运动学求解的空间连续性优势,又考虑了机床受载情况下的变形特点。该方法首先解耦机床多体系统组成,建立体单元移动载荷约束下的刚度模型,基于雅克比传递矩阵建立整机空间误差模型。结合包含空间位置的加工工艺参数,本文方法可以实现复合工艺的加工误差预测,具有很好的通用性,模型流程如图1所示。

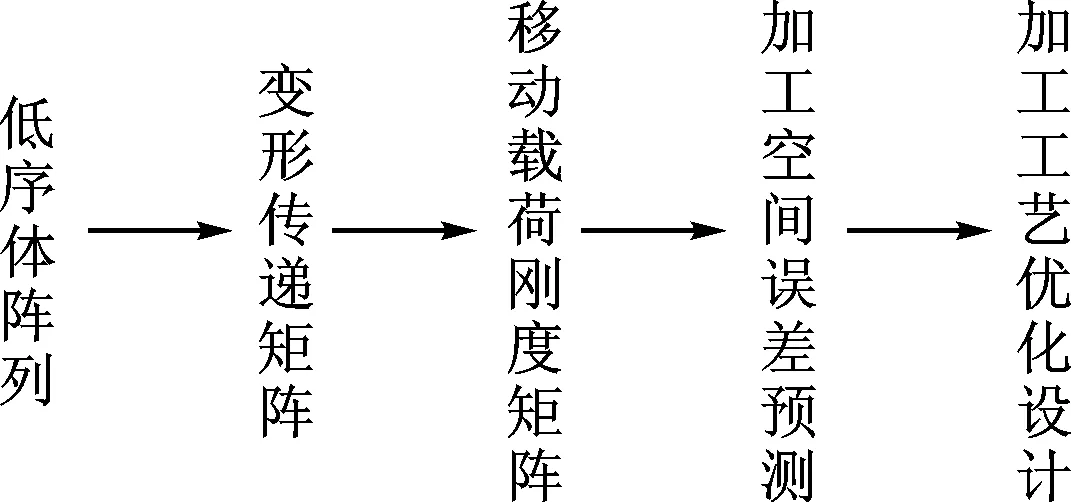
图1 空间刚度建模流程图

1 机床柔性多体系统变形传递分析

多体系统是对工程中复杂机械系统的抽象与描述,多体系统的拓扑结构关系描述尤其适合具有相对运动机械机构的误差建模问题之中,目前已应用于机器人、机床、卫星等复杂机械的误差分析之中。

在多体系统中,体与体、体与系统之间相对位置关系由包含位置与姿态参量的空间坐标系决定。如果在整个多体系统中设定整体坐标系,个体中设定子坐标系,体与体,体与整体空间的位姿问题可以转化为整体坐标系与子坐标系的位姿问题,从而实现多体系统变形的计算。要进行变形计算,首先采用低序体阵列方法描述多体系统拓扑结构的关联关系,进而分析体系统的变形关联关系。在如图2所示的多体系统中,选取惯性参考系R为B0体,任选一个结构体为B1体,之后按远离B1体的方向从一个分支到另一分支依次为其他各体编号。从多体系统中任选Bj体作为一个典型体,则该Bj体的n阶低序体的序号定义为

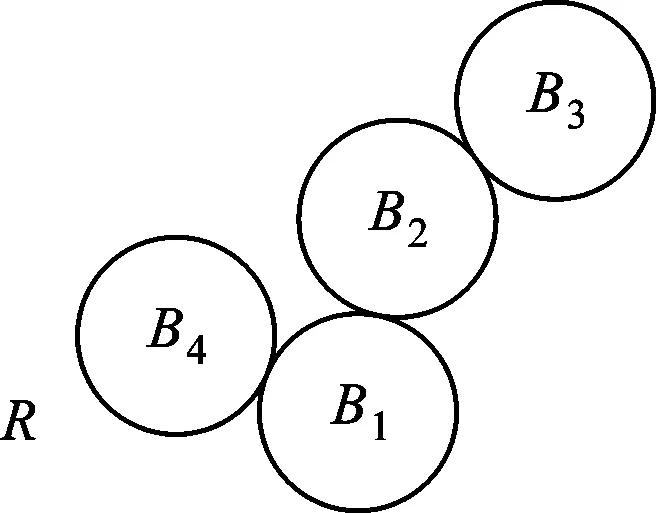
图2 多体系统拓扑结构图

(1)

式中:L为低序体的算子,并且将体Bj称为Bi的n阶高序体,并且满足

Ln(j)=L(Ln-1(j))

(2)

根据式(1)和式(2)可以求解出如图2所示的多体系统中任一体的各阶低序体序号,从而可以得到如表1所示的多体系统的低序体阵列。

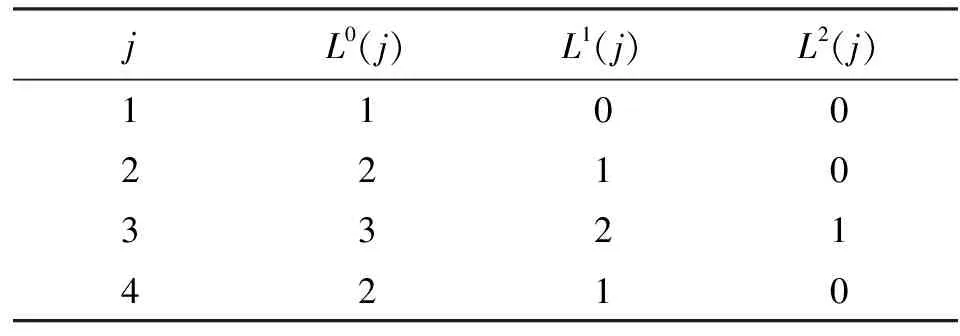
表1 多体系统拓扑结构的低序体阵列

各部件以及终端位置在自身局部坐标系下的变形和在整体坐标系下的位移关系可表示为

(3)

式中:Δ为以地面为基准的整体坐标系下各部件的关键几何特征的方位变化量;δ为各部件局部坐标系下由于自身变形引起的该部件关键几何特征方位的变化量;Tj表示部件j的关键几何特征的方位变化量δj对部件j-1关键几何特征的方位变化量Δj-1的位移传递关系。

2 基于空间刚度场的加工误差模型

根据多体系统运动学理论,部件变形累积得到机床加工变形误差。在加工过程中部件变形误差主要由部件受载引起,受载变形大小决定于部件刚度与受载值。部件刚度受限于部件结构,加工受载与加工工艺相关。

2.1 移动载荷约束下的刚度求解

获取机床部件及整机的刚度最常用的手段包括有限元分析法与解析法两种。有限元分析法能够求解复杂结构的刚度,但是对于处理移动载荷下的结构刚度还不完善;解析法能够在具体分析结构参数的基础上,结合经典刚度计算模型进行刚度求解,对于移动载荷也有很好的求解效果,然而复杂结构建模过程复杂,且不具备良好的通用性。

根据机床部件的结构特点,部件受载分为固定载荷与移动载荷两种情况。其中,固定载荷刚度可通过有限元工具或者实验测量方法得到;对于移动载荷,结合有限元分析与解析法,通过提取载荷点约束下的部件刚度,运用最小二乘法进行数据拟合,实现移动载荷作用下的部件刚度矩阵求解。

对于如图3所示的部件i来说,某一点受到单向载荷作用下会产生6个方向的变形,各部件的6向变形最终均会累积至加工末端,从而造成加工误差。部件在6方向载荷作用下产生的6个方向的变形,其中δxy表示在Fy载荷作用下x方向的位移变形,εxy表示在Fy载荷作用下x方向的角度变形。根据胡克定律,已知部件在载荷作用下的6个方向的变形,进而可以求得部件在6个方向的刚度矩阵。

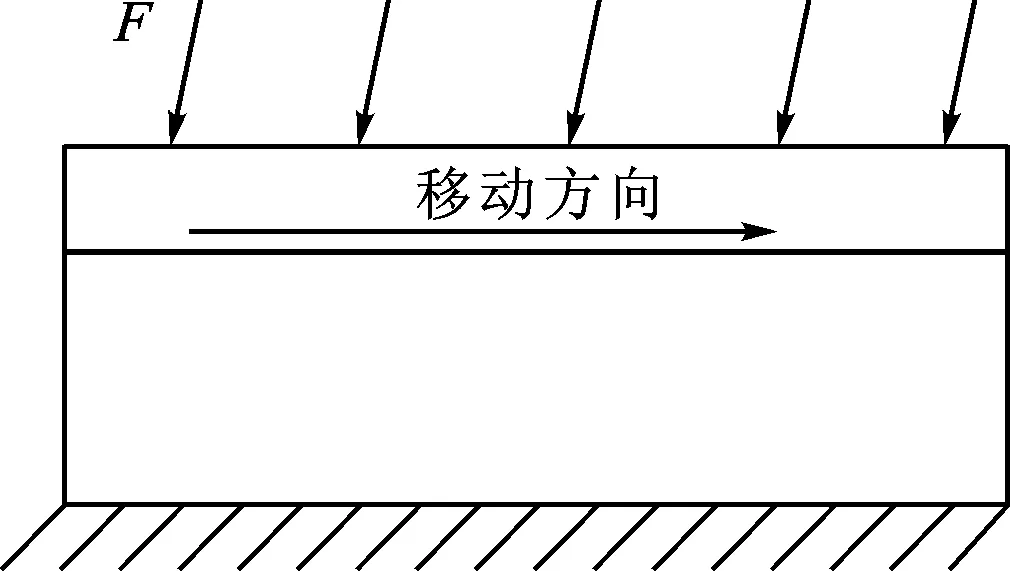
图3 部件i受载示意

当存在移动载荷作用时,假定载荷作用点上存在多个离散点,运用最小二乘法,建立包含运动轴的体单元移动载荷刚度矩阵。如图4所示,已知矩形域上的插值数据点(xi,yi)的值f(xi,yi)构建x、y的二元多项式P(x,y)(x,y次数不超过两次),使其满足插值条件P(xi,yi)=f(xi,yi),i,j=0,1,2。根据9个插值数据点的坐标(xi,yi)及其相应的函数值f(xi,yi),i,j=0,1,2,可列出下式

图4 矩形域上的插值数据点

(4)

令

式中:U、V均为3阶Vandermonde矩阵。将F=UAVT变换为A=U-1F(VT)-1之后,根据式(4)即可求得所需的二元插值多项式

P(x,y)=XAYT=XU-1F(YV-1)T

(5)

通过式(5)进行编程即可实现该算法,从而求得包含位置信息的机床刚度矩阵。

2.2 切削工艺模拟

在加工过程中,主切削力方向仅与刀具坐标系相关,而机床加工误差方向为机床空间笛卡尔坐标系。为了便于进行加工误差求解,需要对切削力进行整机坐标系下的一致性转换,实现工艺与误差关联。

图5为空间6向载荷等效模拟切削工艺的示意图,切削工艺主要通过切削参数来表征,结合工件、刀具结构与材料参数,通过传统的切削力求解模型,可以实现任意切削工艺下的切削力计算。通过子坐标系与整体坐标变换,即可实现切削力的6向载荷的等效转换,进而实现6向载荷下的切削工艺模拟。

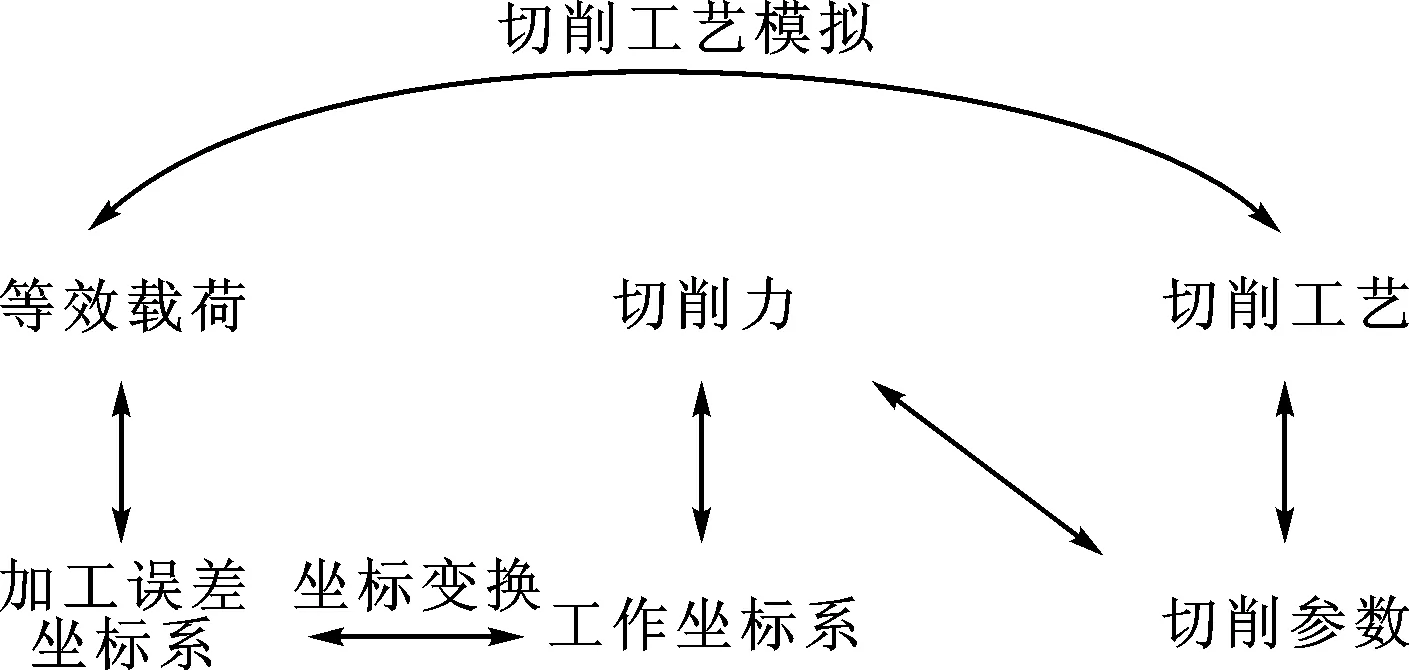
图5 切削工艺模拟

机床切削工艺包括车削、铣削、镗削等,由于刀具的切削方式不同,6向等效载荷的转化方程也有所差异,以周铣、顺铣为例进行切削力等效转换。将主切削力Fc分别向x、y两个方向正交分解,分解结果如图6所示,主切削力Fc沿x方向的分力Fcx由Fcx1到Fcx2,沿y方向的分力Fcy由0到Fcy2。因此,在进行切削力模拟过程中,只需模拟主切削力Fc沿x方向的分力Fcx及沿y方向的分力Fcy的均值作为加载切削力即可。

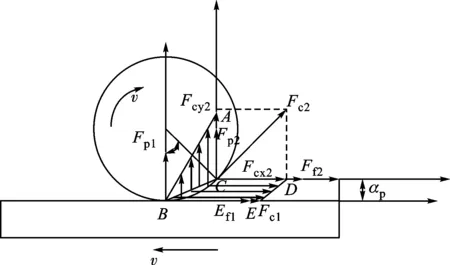
图6 周铣、顺铣切削力转换示意图

基于体单元变形影响规律,建立加工空间内零件加工表面的形貌描述方程,同时关联加工轨迹所在位置的加工工艺,可以计算出机床加工终端任意加工位置的切削力,从而实现加工表面形貌的误差预测。

2.3 空间加工误差建模

假定工件表面形貌描述模型为f(x,y,z),加工表面任意位置所对应的切削力为F(f(x,y,z))。切削力可以针对不同的加工工艺、不同工况进行计算,如不同的切削方式对应不同的切削载荷求解公式。在同一切削方式下,由于毛坯表面加工误差影响切削过程中的切削深度,使得切削载荷发生变化,从而造成加工误差复映现象等。通过关联切削力与形貌描述模型,联立可得机床加工形貌的误差模型为

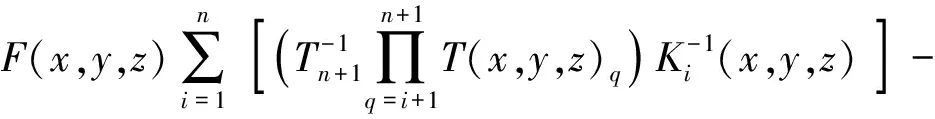
(6)

3 实例应用

以精密坐标镗铣加工中心加工发动机壳体为例,进行加工误差预测与优化设计。THM46100加工中心包含3根直线轴,1根回转轴,加工空间为x向1 200 mm,y向1 100 mm,z向1 200 mm。机床主要包括床身、立柱、滑鞍、主轴箱、工作台等部件,其中床身上安装z向行程导轨,工作台在z向滑动;工作台部件包含B轴回转运动;立柱安装有x向行程导轨,滑鞍在立柱上滑动;滑鞍上装有y向行程导轨,主轴箱在y向滑动。机床的结构如图7所示,根据实际结构构建多体系统拓扑结构以及低序体阵列描述,从而确定各部件间的变形关联关系。

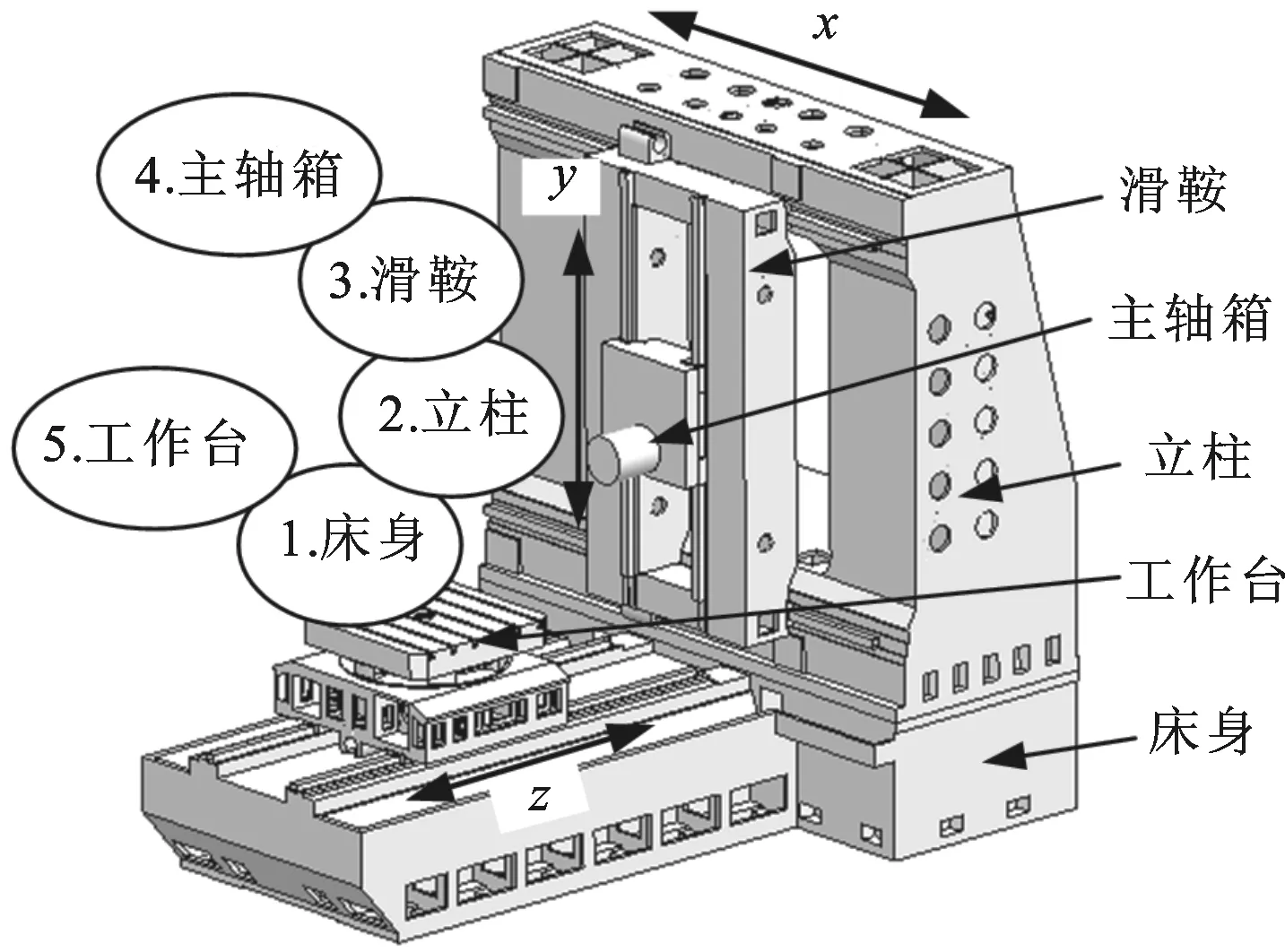
图7 精密卧式加工中心及其拓扑结构图

3.1 复合工艺零件加工误差预测

以发动机壳体为例进行复合工艺误差预测。发动机壳体结构如图8所示,主要包括镗孔、铣端面以及立铣侧面3个复合工艺。

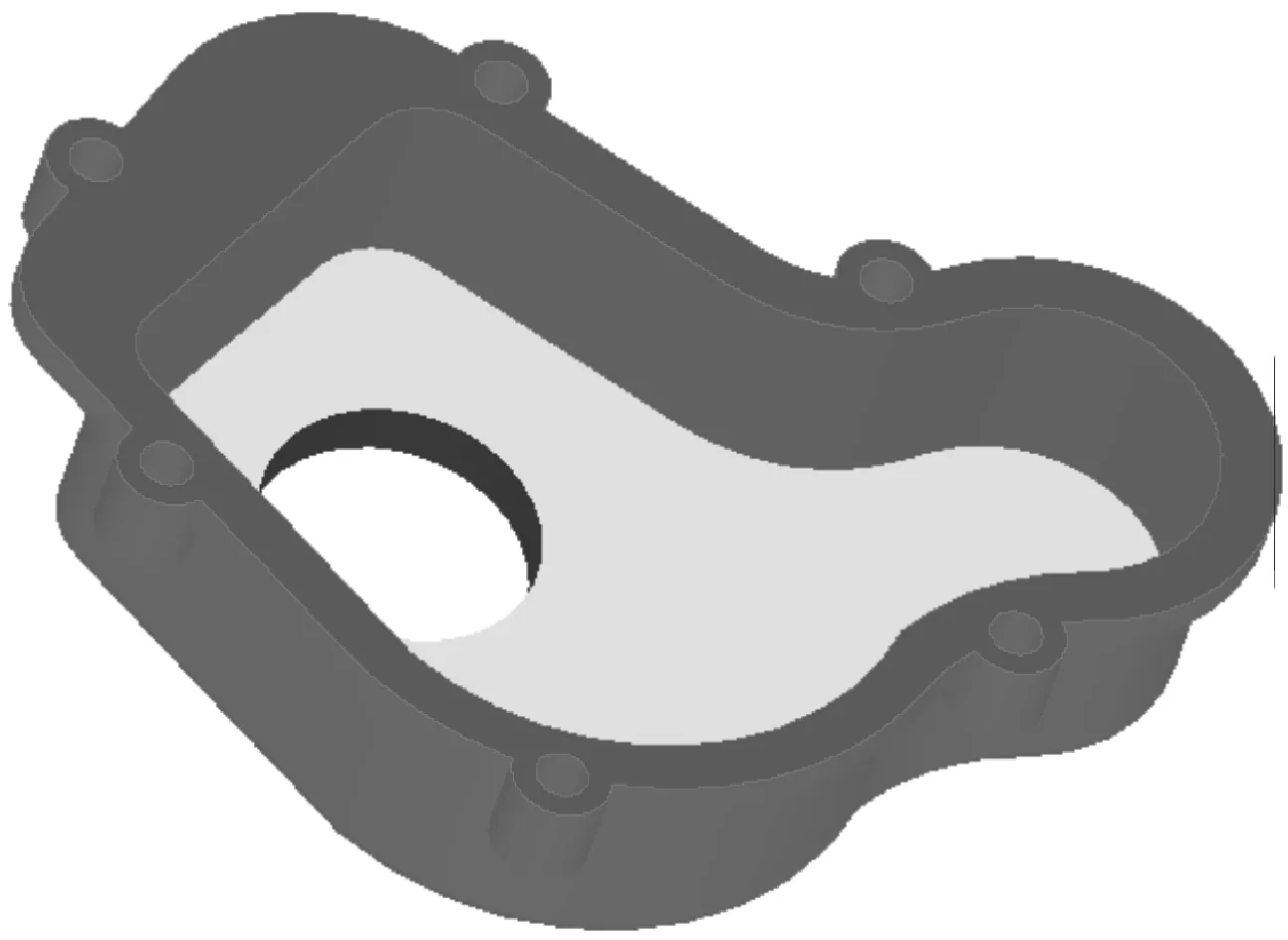
图8 发动机壳体加工表面示意图

以切削力转化理论为基础,根据待加工表面尺寸,分别对端铣、周铣、镗削的切削力进行计算。

(1)端铣:待加工结合面的最小距离为10 mm,采用20 mm端铣刀,齿数为3,铣削宽度ae=10 mm,切削深度ap=4 mm,每齿进给量fz=0.09 mm。

(2)周铣:箱壳内壁采用圆柱铣刀,加工最小直径为60 mm,刀具直径为50 mm,齿数为8,铣削宽度ae=3 mm,切削深度ap=2 mm,每齿进给量fz=0.25 mm。

(3)镗削:采用双刀镗削,待镗孔直径为70 mm,切削深度ap=1 mm,每齿进给量fz=0.25 mm。

对切削载荷进行等效转换,可得各向载荷计算结果如表2所示。

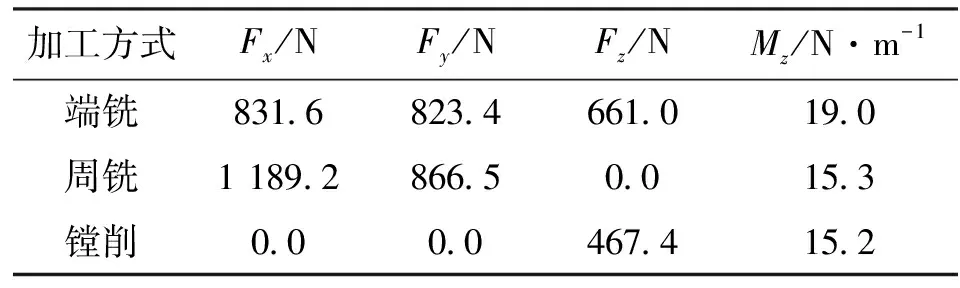
表2 壳体加工过程中的各向载荷

基于加工误差预测理论模型分别对结合面、底面、内表面、轴承孔的加工精度进行预测。在THM46100加工中心上进行端铣,加工结合面与底面,重点对影响加工质量的z方向加工误差进行分析,端铣结果如图9所示。对于端铣结合面,z方向最大加工误差为17.23 μm,最小加工误差为11.44 μm;对于端铣底面,最大加工误差为19.67 μm,最小加工误差为15.22 μm。底面与结合面的加工误差趋势一致,z方向加工误差在y方向的变化量明显大于x方向,这主要是由于机床y方向的刚度变化大于x方向的变化所引起的。结合面加工误差整体小于底面加工误差,这是由于沿z方向刚度发生了变化,在相同工艺情况下,刚度变化对加工误差会产生主要影响。

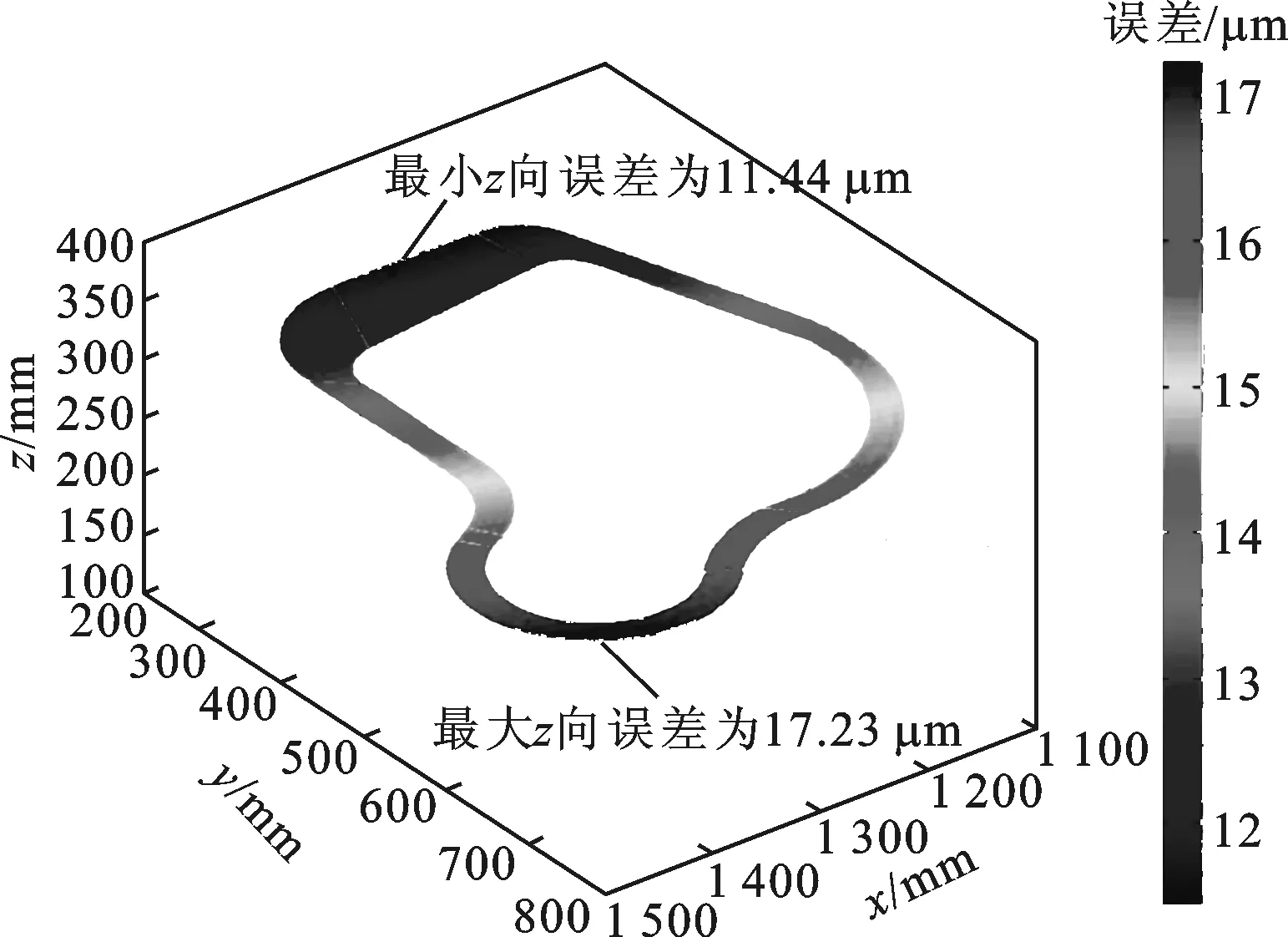
(a)端铣结合面

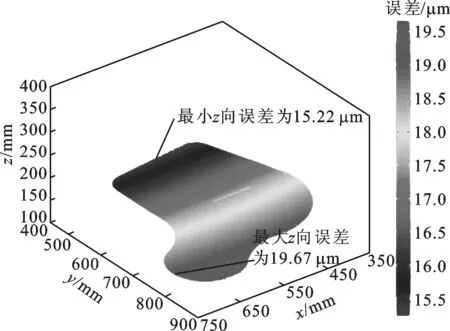
(b)端铣底面图9 端铣工艺下的加工精度预测

对于周铣内表面,加工误差与方向随内表面而改变,因此将加工误差分解为x、y两个方向进行分析。由图10可以看出,在周铣结合面过程中,x方向最大误差为10.5 μm,最小误差为7.96 μm;y方向的最大误差为-19.06 μm,最小误差为-16.41 μm。x、y方向加工误差的变化情况与端铣误差变化一致,即刚度场为影响加工误差的主要因素。

在镗削过程中,由于加工面也是圆环面,因此需要对x、y方向误差进行分析。由图11可知,镗削轴承孔过程中,x方向的加工误差较小,可以忽略不计,y方向的加工误差相对较大。在镗削过程中,最大加工误差为-21.91 μm,最小加工误差为-21.02 μm。

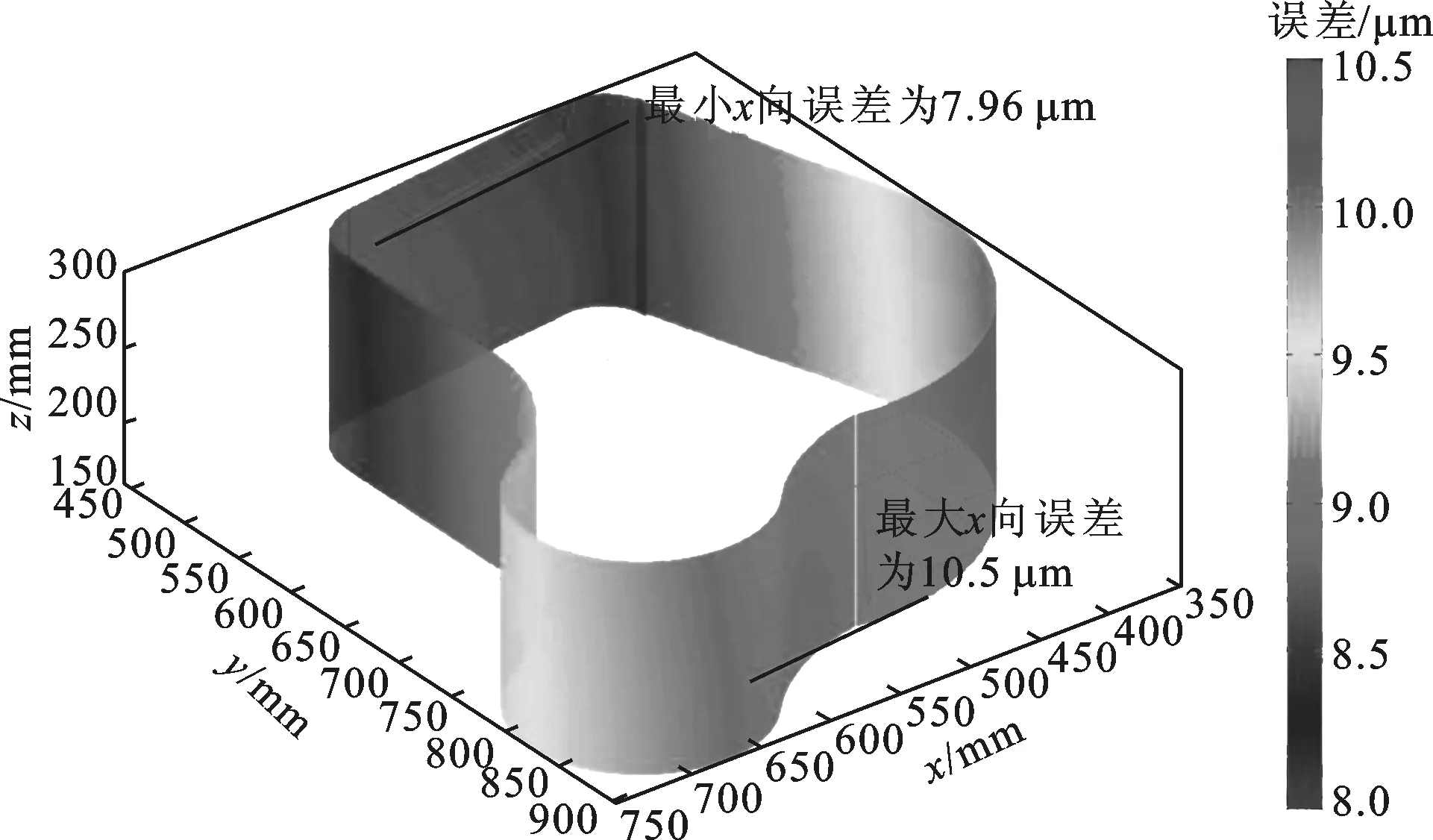
(a)x方向误差

从发动机壳体精度预测来看,各待加工面的最大加工误差不超过25 μm,且总体趋势趋于一致,这是由于机床空间刚度变化所产生的变形影响大于切削参量变化,要提高加工精度可以从刀轨路径规划与装夹位置进行调整。

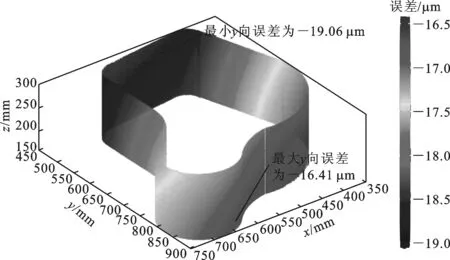
(b)y方向误差图10 发动机壳体待加工面在周铣工艺下的精度预测

3.2 切削工艺优化

结合面的加工误差关系到发动机箱壳能否正常装配及是否具有良好的机械性能。以结合面的平面度作为衡量其加工误差的指标,结合面的加工误差关系到发动机箱壳能否正常装配及是否具有良好的机械性能。以结合面的平面度作为衡量加工误差指标,对发动机壳体进行工艺优化。如图12所示,以原有装夹方式为基准,将壳体分别顺时针旋转90°、180°、270°,精度预测结果如表3所示。

对于本结合面,以最大、最小误差之间的平均值为理想平面,以最大加工误差和最小加工误差之差作为衡量平面度的标准,对4种装夹方式加工平面度进行比较。结合面加工方式为铣削,x、y方向的加工误差对于结合面的加工精度影响不大,因此只关注结合面在z方向由于机床刚度引起的加工误差。

(a)x方向误差

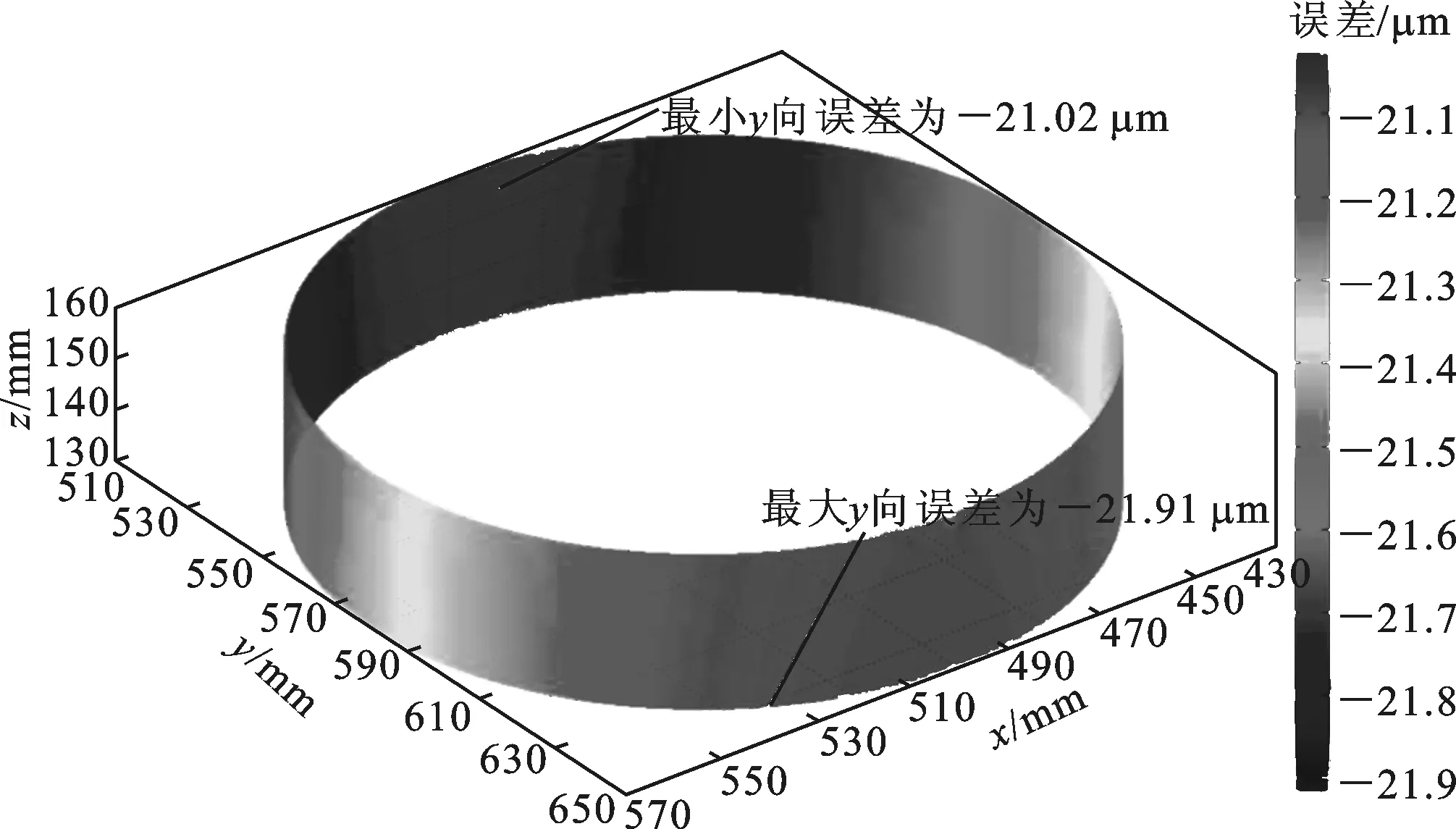
(b)y方向误差图11 发动机壳体轴承孔在镗削工艺下的精度预测

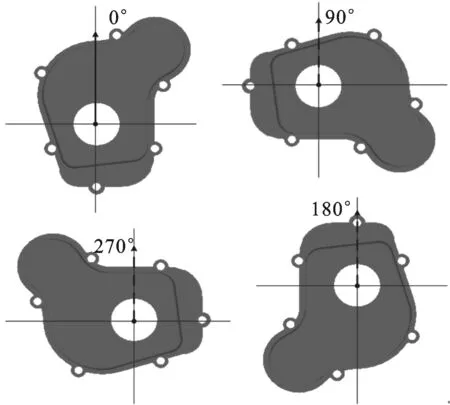
图12 4个装夹角度示意图

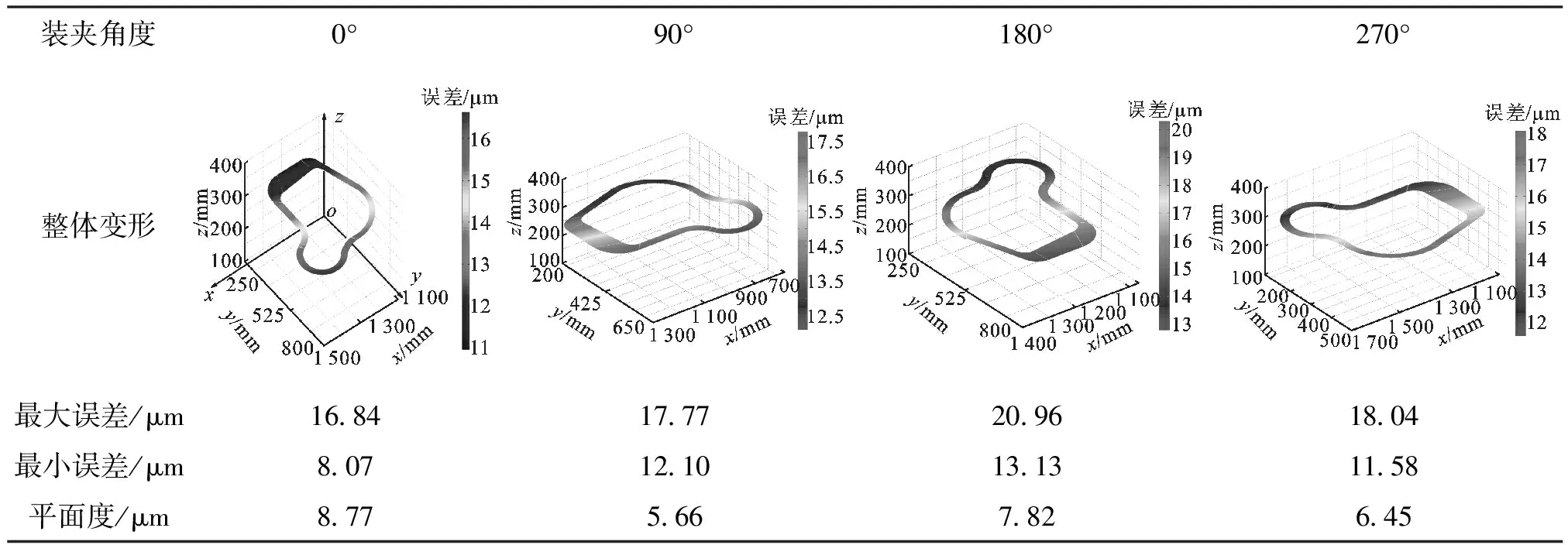
装夹角度0°90°180°270°整体变形最大误差/μm1684177720961804最小误差/μm807121013131158平面度/μm877566782645

从表3中可知,当装夹位置角度为90°时,结合面的z向加工误差较小,平面度最好。以装夹角度为横坐标,以平面度误差为纵坐标,对各角度下的平面度误差进行曲线拟合,如图13所示。

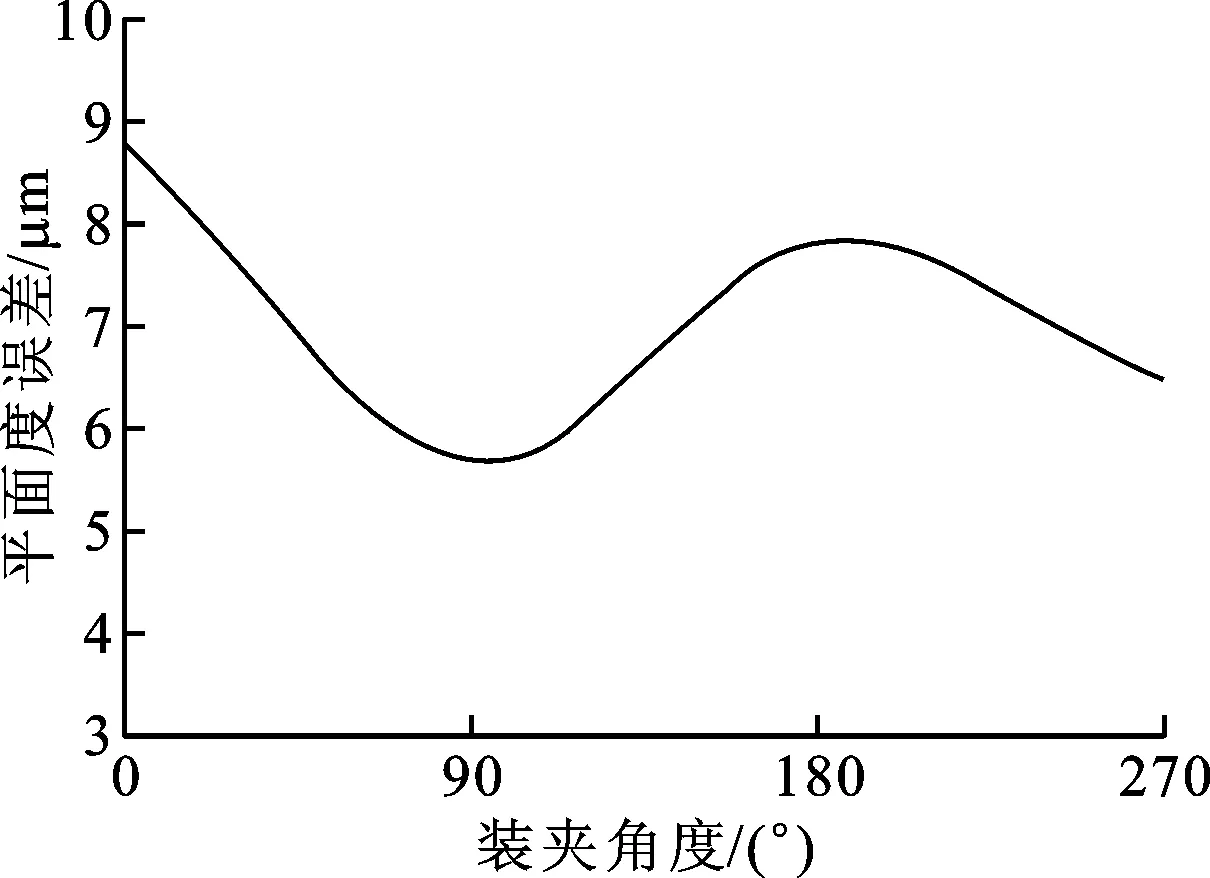
图13 装夹角度与平面度的关系

从装夹角度与平面度拟合曲线看出,随着角度的变化,平面度先减小后增大,90°与270°时的平面度要小于0°与180°。综合考虑装夹可行性、z向加工误差以及平面度,本结合面加工装夹角度为90°时,平面度误差为5.66 μm,加工精度提高了35%。

4 结 论

本文基于多体系统理论,以低序体阵列与传递矩阵来描述机床的运动关联关系。采用最小二乘法对移动载荷约束下的机床刚度场进行建模,结合加工工艺模拟方法实现了机床空间加工误差的建模。本模型具有很强的通用性,可以广泛地应用于复合加工工艺约束下的误差预测。以精密坐标镗铣床加工发动机壳体为例,进行了镗削、铣削等复合工艺的误差预测,结果显示,本文方法可以对空间工艺的加工误差进行预测。基于加工误差预测模型,通过改变装夹角度实现了加工误差的优化,优化结果显示,当装夹角度为90°时,平面度误差最小,加工精度可提升35%。本文方法采用部件刚度组合计算,实现机床空间刚度求解,针对复合工艺的误差预测具有很好的通用性,因此在机床的工艺设计阶段的加工优化具有很好的应用前景。

[1] 卢秉恒. 机械制造技术基础 [M]. 北京: 机械工业出版社, 2007: 24-25.

[2] 黄克, 关立文, 杨亮亮, 等. 基于“S”形试件的五轴机床几何误差建模研究 [J]. 机械设计与制造, 2015(2): 189-197. HUANG Ke, GUAN Liwen, YANG Liangliang, et al. Geometric error modeling of five-axis CNC machine tools based on “S” shaped test piece [J]. Machinery Design & Manufacture, 2015(2): 189-197.

[3] FU Guoqiang, FU Jianzhong, XU Yuetong, et al. Product of exponential model for geometric error integration of multi-axis machine tools [J]. Int J Adv Manuf Technol, 2014, 71: 1653-1667.

[4] CHEN G S, MEI X S, LI H L. Geometric error modeling and compensation for large-scale grinding machine tools with multi-axes [J]. Int J Adv Manuf Technol, 2013, 69: 2583-2592.

[5] 康念辉, 李圣怡, 郑子文. 基于多体系统理论的非球面磨削误差模型与补偿技术 [J]. 机械工程学报, 2008, 44(4): 143-149. KANG Nianhui, LI Shengyi, ZHENG Ziwen. Error model and compensation technology of aspheric grinding based on multibody system theory [J]. Chinese Journal of Mechanical Engineering, 2008, 44(4): 143-149.

[6] 杨程旭, 郑煜, 徐洲龙. 多体系统理论的四轴运动平台综合空间误差建模 [J]. 现代制造工程, 2009(4): 1-4. YANG Chengxu, ZHENG Yu, XU Zhoulong. The universal volumetric error modeling of a four-campaign platform based on the multi-body system theory [J]. Modern Manufacturing Engineering, 2009(4): 1-4.

[7] 范晋伟, 费仁元, 田越, 等. 基于多体系统运动学理论的并联机床运动空间分析及仿真研究 [J]. 机械工程学报, 2001, 37(1): 32-36. FAN Jinwei, FEI Renyuan, TIAN Yue, et al. Study on the movement volume analysis and simulation method for parallel machine tool based on multi-body system [J]. Chinese Journal of Mechanical Engineering, 2001, 37(1): 32-36.

[8] DING Shuang, HUANG Xiaodiao, YU Chunjian, et al. Identification of different geometric error models and definitions for the rotary axis of five-axis machine tools [J]. International Journal of Machine Tools and Manufacture, 2016, 100(1): 1-6.

[9] 李学伟, 赵万华, 卢秉恒. 轨迹误差建模的多轴联动机床轮廓误差补偿技术 [J]. 西安交通大学学报, 2012, 46(3): 47-52. LI Xuewei, ZHAO Wanhua, LU Bingheng. Contour error compensation strategy for multi-axis machining by trajectory error modeling [J]. Journal of Xi’an Jiaotong University, 2012, 46(3): 47-52.

[10]闫蓉, 陈威, 彭芳瑜, 等. 多轴加工系统闭链刚度场建模与刚度性能分析 [J]. 机械工程学报, 2012, 48(1): 177-184.

YAN Rong, CHEN Wei, PENG Fangyu, et al. Closed-loop stiffness modeling and stiffness index analysis for multi-axis machining system [J]. Chinese Journal of Mechanical Engineering, 2012, 48(1): 177-184.

[11]DE LACALLE L N L, LAMIKIZ A. Machine tools for high performance machining [M]. Berlin, Germany: Springer-Verlag, 2009: 46-52.

[12]CHANAL H, DUC E, RAY P. A study of the impact of machine tool structure on machining processes [J]. International Journal of Machine Tools & Manufacture, 2006, 46(2): 98-106.

[13]刘海涛, 赵万华. 基于广义加工空间概念的机床动态特性分析 [J]. 机械工程学报, 2010, 46(21): 54-60. LIU Haitao, ZHAO Wanhua. Dynamic characteristic analysis for machine tools based on concept of generalized manufacturing space [J]. Chinese Journal of Mechanical Engineering, 2010, 46(21): 54-60.

[14]GUYAN R J. Reduction of stiffness and mass matrices [J]. AIAA Journal, 1965, 3(2): 380-380.

[15]芮筱亭, 戎保. 多体系统传递矩阵法研究进展 [J]. 力学进展, 2012, 42(1): 4-16. RUI Xiaoting, RONG Bao. Advances in transfer matrix method for multibody system dynamics [J]. Advances in Mechanics, 2012, 42(1): 4-16.

[16]吕亚楠, 王立平, 关立文. 基于刚度组集的混联机床的静刚度分析与优化 [J]. 清华大学学报: 自然科学版, 2008, 48(2): 180-183. LÜ Yanan, WANG Liping, GUAN Liwen. Stiffness analysis and optimization of a hybrid machine tool based on the stiffness matrix [J]. Journal of Tsinghua University: Science and Technology, 2008, 48(2): 180-183.

[本刊相关文献链接]

周强,刘志刚,洪军,等.卡尔曼滤波在精密机床装配过程误差状态估计中的应用[J].2015,49(12):97-103.[doi:10.7652/xjtuxb201512016]

冯斌,梅雪松,杨军,等.数控机床摩擦误差自适应补偿方法研究[J].2013,47(11):65-69.[doi:10.7652/xjtuxb2013 11012]

李学伟,赵万华,卢秉恒.轨迹误差建模的多轴联动机床轮廓误差补偿技术[J].2012,46(3):47-52.[doi:10.7652/xjtuxb 201203009]

马晓龙,陈贵灿.固定位宽乘法器的量化误差补偿方法及电路实现[J].2011,45(12):75-81.[doi:10.7652/xjtuxb2011 12014]

留剑,洪军,杨朝晖,等.高速精密角接触球轴承旋转精度创成机理研究[J].2011,45(11):72-78.[doi:10.7652/xjtuxb 201111014]

邓星桥,向中凡,王进戈.加工和安装误差对无侧隙蜗杆传动接触线及齿廓的影响[J].2011,45(2):111-116.[doi:10.7652/xjtuxb201102023]

陈光胜,梅雪松,陶涛.X-Y工作台摩擦误差补偿方法的研究[J].2011,45(1):69-73.[doi:10.7652/xjtuxb201101014]

周玉清,陶涛,梅雪松,等.旋转轴与平移轴联动误差的快速测量及溯源[J].2010,44(5):80-84.[doi:10.7652/xjtuxb 201005017]

(编辑 杜秀杰)

Prediction of Machining Error for Machine Tool Multi-Body System Restrained by Stiffness Field

GAO Xianming1,HONG Jun1,ZHEN Yichao2

(1. State Key Laboratory for Manufacturing System Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Xi’an JingDiao Software Technology Co. Ltd., Xi’an 710119, China)

A novel method for machine tool multi-body system restrained by stiffness field is proposed to solve the difficulty of discontinuous machining error prediction result. According to the characteristics of multi-body system kinematics solution, the machine tool component is considered as an elastic body, and the lower body array and transfer matrix are used to describe the motion relationship between the machine tool components. Following the condensation approach of stiffness matrix and the least square evaluation, the stiffness model under moving load of machine tool component can be obtained. Then Jacobian matrix is taken to construct the machining error prediction model. This method is verified in a boring milling machining error prediction for an engine cylinder head. The combined machining error prediction method enables to optimize the angle of clamping in engine shell machining process. Describing multi-body system by lower body array facilitates evaluating errors in united machining process. According to the combined machining error prediction, the machining precision can be increased by 35% at working degree of 90°.

numerical control machine tool; multi-system theory; error prediction; manufacturing space; process optimization

2015-11-25。 作者简介:高羡明(1984—),男,博士生;洪军(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51575428);国家“863计划”资助项目(2012AA040701);国家重大专项资助项目(2015ZX04014 021)。

时间:2016-03-15

10.7652/xjtuxb201606014

TG502.1

A

0253-987X(2016)06-0090-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160315.1632.004.html