MEMS陀螺随机误差趋势项的支持向量回归机预测补偿算法

成 雨，叶 东，孙兆伟

（哈尔滨工业大学 卫星技术研究所，哈尔滨 150001）

MEMS陀螺随机误差趋势项的支持向量回归机预测补偿算法

成 雨，叶 东，孙兆伟

（哈尔滨工业大学 卫星技术研究所，哈尔滨 150001）

为了适应低成本快速响应卫星的发展趋势，越来越多的卫星采用了MEMS陀螺系统与信息融合方法相结合的设计方案。为提高传统的基于自回归滑动平均（Auto-Regressive and Moving Average，ARMA）模型和支持度的信息融合方法的精度，抑制随机误差趋势项对卫星稳定控制的不利影响，提出了一种基于支持向量回归机（Support Vector Regression，SVR）的预测补偿算法。该算法对各个MEMS陀螺输出数据进行滤波，并提取相应的随机误差趋势项，通过相空间重构获得训练样本并进行SVR建模，用以实时补偿。然后使用低成本商用器件搭建了MEMS陀螺系统，并在单轴气浮转台上进行了实验。实验结果表明，预测补偿算法使得MEMS陀螺系统输出数据的方差降为原先的31.39%，融合精度得到了显著的提高。

微机电陀螺；时间序列；支持向量机；相空间重构

传统卫星的设计制造过程具有成本高、耗时长的特点，不利于卫星技术在快速响应任务中的应用。商用现货MEMS（Micro Electro Mechanical System）元器件体积小、重量轻、成本低，能够有效提高卫星的功能密度，缩短研制周期，为卫星快速设计制造提供了思路。在这一思路的指导下，各国均有采用MEMS陀螺作为姿态确定系统的卫星问世，如斯坦福大学的QuakeSat，东京工业大学的 Cute-1.7+APD2，哈尔滨工业大学的紫丁香2号等。为了适应快速响应任务，加快卫星设计制造进程，以MEMS陀螺构成的卫星姿态确定系统越来越受到关注[1-2]。

由于工艺水平的限制，MEMS陀螺在精度和可靠性方面尚存在劣势，无法替代高精度姿控系统中的传统陀螺。为了满足卫星姿态确定系统的设计要求，可以采取两种策略：一是大幅提高 MEMS陀螺测量精度，使之能够匹敌传统陀螺；二是通过设计体系结构，使用多个MEMS陀螺，构建联合姿态测量系统，并采用信息融合算法提高测量系统的精度。由于前者会大幅增加整星成本，降低任务预期收益，因此后一种策略得到了学者们更多的研究[3]。

一般地，MEMS陀螺信息融合算法首先对随机误差进行建模，然后应用所建模型从量测数据中估计出真实状态。时间序列模型将随机误差看成是平稳线性的时间序列，常利用自回归滑动平均算法（Auto-Regressive and Moving Average，ARMA），假设 MEMS陀螺量测噪声为历史数据和历史白噪声的线性组合。这种方法建立的线性模型可以方便地应用于 Kalman滤波器中，能够有效地抑制随机误差[4]。但这种建立在线性平稳假设之上的方法，对MEMS陀螺随机误差的建模必然会存在误差。为了克服这一缺陷，文献[5]和文献[6]提出了基于小波变换的数据处理方法。该方法由Fourier变换发展而来，通过小波基和mallat算法，能够同时在频域和时域中对指定信号进行细分，可以获得更多的细节，从而有利于数据降噪[7]。但该方法为事后处理，实时性次于 Kalman滤波。另一方面，文献[8]和文献[9]使用神经网络替代ARMA模型。神经网络理论上可以逼近任意的非线性函数[10]，因此所建立的模型能够较好地适应随机误差的非线性。但是，神经网络遵循经验风险最小（Empirical Risk Minimization，ERM）的原则，当样本较少时，由于未考虑模型的置信风险，存在过学习问题。

为了保证MEMS陀螺信息融合方法的实时性，本文使用了基于 ARMA模型和支持度的 Kalman滤波器，同时针对线性模型精度的不足，提出了利用泛化性能更优的支持向量回归机（Support Vector Regression，SVR）对MEMS陀螺随机误差趋势项进行预测补偿。

1 基于ARMA模型的Kalman滤波

补偿确定性误差后，MEMS陀螺输出值可以看作是由真实角速率kΩ和随机误差kε所组成的。对随机误差kε进行ARMA建模：

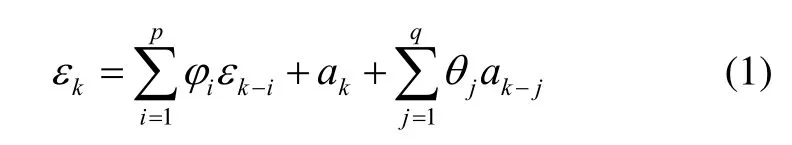
式中：kε为k时刻的随机误差，ak为k时刻的白噪声，iφ为自回归参数，jθ为滑动平均参数。为了便于观测真实角速率kΩ，本文将其扩充在滤波器状态变量中。在卫星姿态保持阶段和匀速机动过程中，可以认为wk为白噪声序列。因此Kalman滤波的系统方程可以写为：

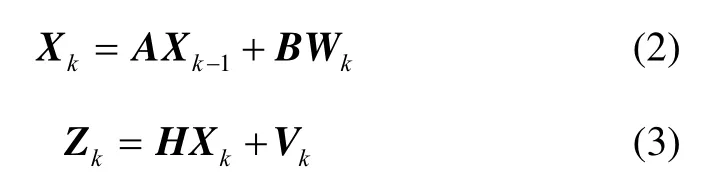
2 基于支持度的权值分配方法

本文研究的MEMS陀螺系统由6个陀螺构成，每个陀螺的输出可以看作是真实角速率和噪声的叠加，即

每个 MEMS陀螺对同一输入角速率进行冗余测量，其输出结果可以相互仲裁。当某一陀螺量测值明显异于其它陀螺，则说明该陀螺不可靠，支持度低，因此在融合过程中给予较小的权值，抑制其对整个量测系统的不利影响。本文使用支持度函数衡量各个陀螺量测值之间的差异。

对于理想的支持度函数，当两个样本点距离接近时，即相互支持度较高时，支持度函数值应当快速上升，反之则快速下降。因此使用 KMOD核函数[11]作为支持度函数。k时刻第 j个敏感器对第i个敏感器量测值的支持度为

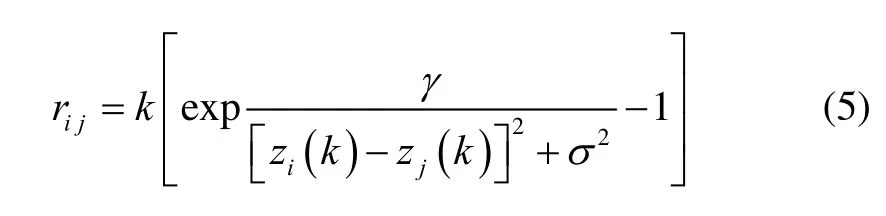
式中：k、γ和σ为可调参数，用于调节支持度对量测值差异的敏感度。由式(5)构造k时刻批量 MEMS陀螺的支持度矩阵

和综合支持度函数

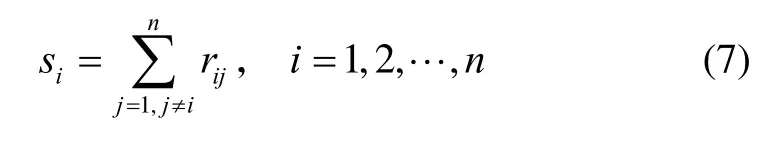
为了简化计算，对式(7)进行归一化处理，定义一致性度量：

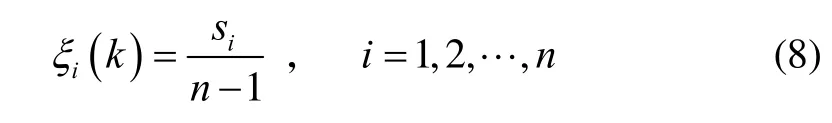
陀螺数据的可靠性由当前时刻和历史时刻的一致性度量共同决定，当MEMS陀螺历史时刻的一致性度量均较高，说明陀螺可靠，数据稳定，应给予较大的权值。

k时刻第i个陀螺量测值的一致性均值为

一致性方差为

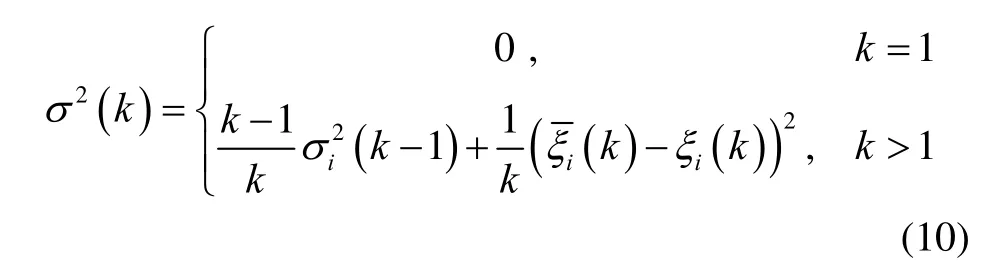
由式(9)和式(10)可以得到k时刻第i个陀螺量测值的权值为

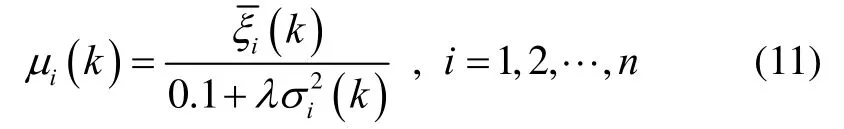
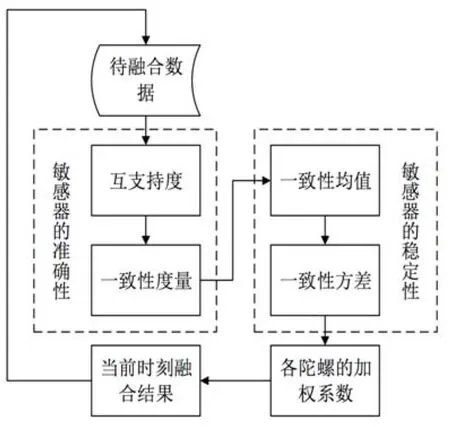
图1 融合算法流程图Fig.1 Flow chart of fusion algorithm

式中：λ为可变参数，可以调节权值分配策略。根据式(11)，状态变量估计值为

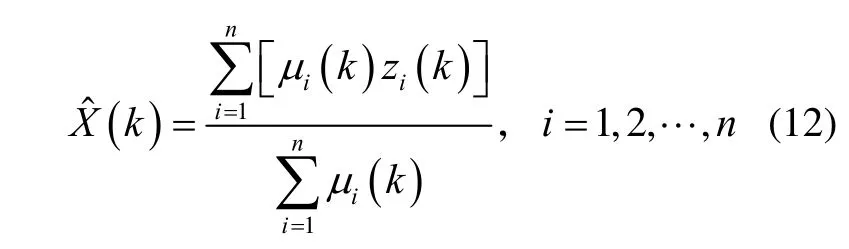
综上所述，融合算法流程如图1所示。

3 基于SVR的趋势项预测补偿算法

从仿真结果中可以看出，经过基于ARMA模型的Kalman滤波器处理后的MEMS陀螺的角速率估计误差由趋势项和高频噪声构成，其中，对角度积分的影响较大，需要将其消除，以降低MEMS陀螺输出数据的方差。由于趋势项真实角速率ω和高频噪声混杂在一起，即

当星上高精度角速率敏感器正常工作时，即存在参考角速率ωref，其值可以看作是真实角速率，即，能够用来标定MEMS陀螺。拟合曲线与真实角速率之差即为趋势项。当参考角速率ωref有效时，对进行SVR建模。

当高精度角速率敏感器短时失效时，批量陀螺系统进入预测校正阶段，以保证短时量测精度。

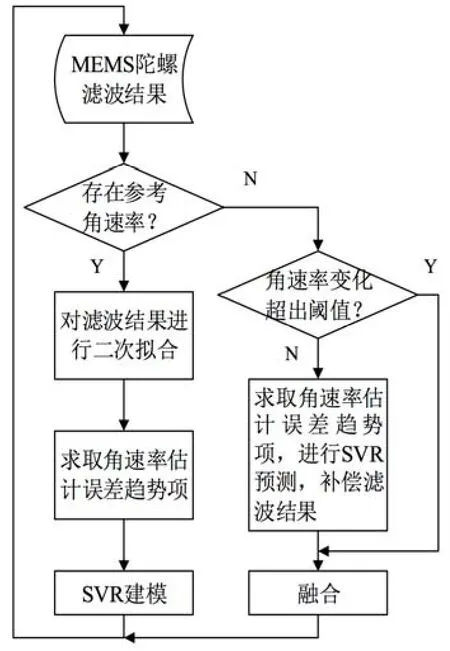
图2 趋势项的预测补偿算法流程图Fig.2 Predictive compensation algorithm of trend term

在卫星进行稳定控制时，可以认为真实角速率ω保持不变。拟合值与真实角速率做差，得到趋势项的当前值，与历史值一同代入 SVR模型中，对下一时刻的趋势项进行预测，从而补偿了趋势项的影响，降低了MEMS陀螺输出数据的方差。

综上所述，基于SVR的趋势项预测补偿算法流程如图 2 所示。

3.1 SVR建模

传统的神经网络方法以 ERM为基础，当样本较少时，即使经验风险很小，训练结果很好，学习机的实际风险也可能很大，这就是 ERM 方法存在的过学习问题。而SRM（Structural Risk Minimization，SRM）综合考虑了训练精度和置信范围，使得学习机的实际风险最小化，避免了过学习问题。

给定训练样本集：

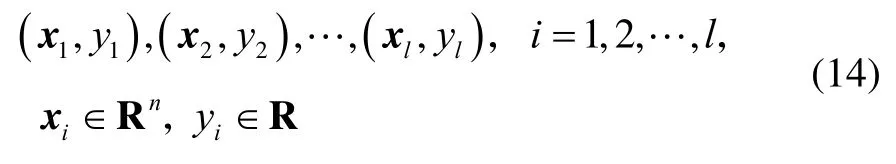
对于给出的训练样本集，回归问题便是寻找一个实值映射 f(·)来描述yi与xi的关系，从而对于任意一个输入x，通过映射 f(·)便可得到输出y。在分类问题中，要求分类超平面使得正反两类样本点的间隔最大。而在回归问题中，要求所有样本点到分类超平面（即回归函数f(x)）的距离尽量小。

对于线性SVR，考虑下面的回归函数：

训练样本为

假设在精度ε下，训练样本存在拟合函数 f( x)，那么寻找最小ω的问题可以写为凸优化问题

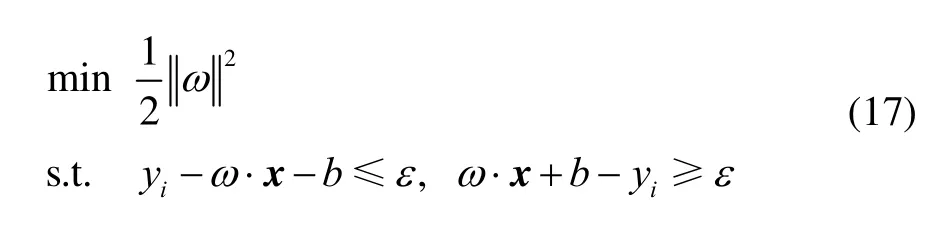
对于某些样本点，函数f( x)在精度ε下无法拟合该样本点，即线性不可分。松弛变量的引入可以解决这一问题，式(17)写为

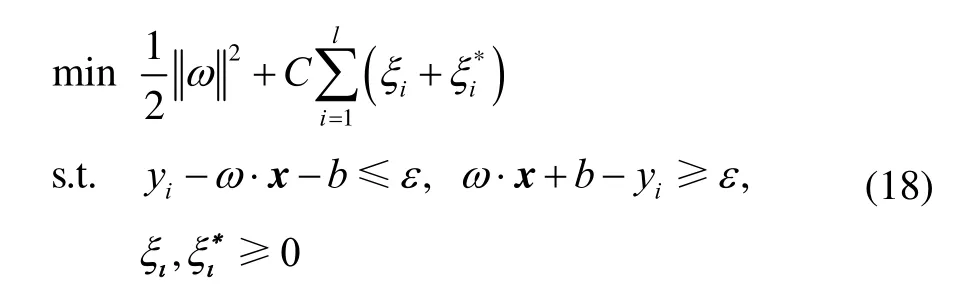
引入Lagrange函数和对偶变量：

选择iα中的一个分量由此计算

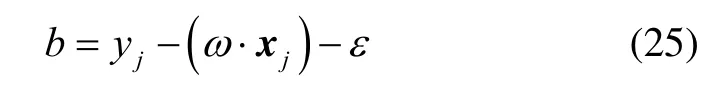
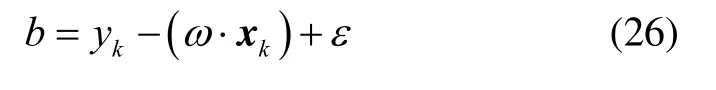
非线性 SVR通过非线性映射Φ(·)将输入样本映射到高维空间，然后在此空间中进行线性回归。由此解决了输入空间不可线性回归的问题。

但是这种提高系统维度的方法增加了计算复杂度，由此引入KMOD核函数，由此计算

对于常用的基于距离的核函数，输入空间内的两点距离越近，其相关性越强，因此需要在计算空间里尽可能将两个点去相关性，同时还要尽可能地保留其它信息。设计的核函数需要拥有如下两种特性：一是在零点附近快速减小，二是在远离零点的区域缓慢下降。为此，N. Ayat[11]等人提出了缓和下降核函数：

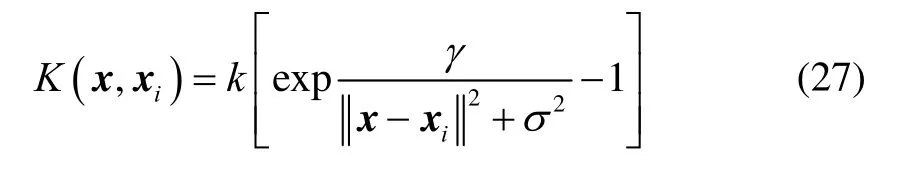
式中：k为常数，可以改变核函数在零点的值；γ和σ为可调参数，用于改变核函数在零点附近的减小速度和核函数宽度。Ayat[11]等人已经证明，在二分类问题中，KMOD核函数能够以最少的支持向量获得最大的分类间隔，具有良好的泛化能力。因此本文使用KMOD核函数构建本章的SVR。

由于核函数的固有属性，可以很好地完成映射，并显著降低计算量，由此优化问题转化为在式(20)的约束下，由

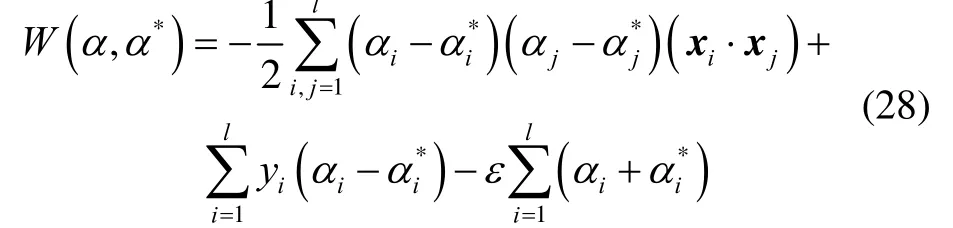
求取

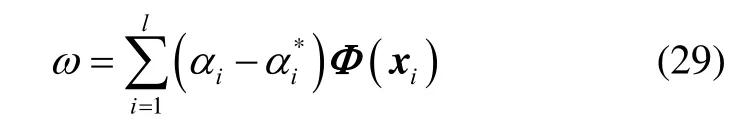
所以回归函数 f( x)就可以写为

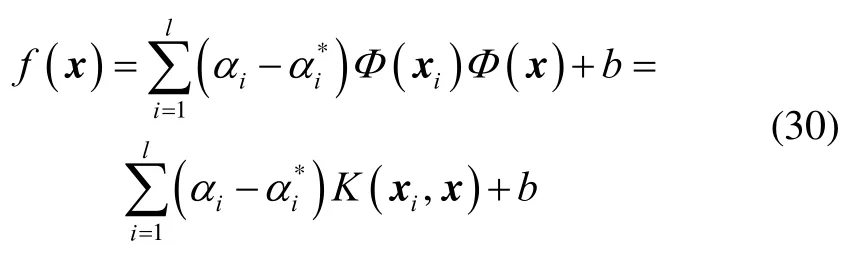
3.2 相空间重构

式中：m为嵌入维数，τ为延迟时间。

4 仿真结果及分析

为了验证上述方法的有效性，本节使用低成本商用器件搭建的 MEMS陀螺硬件系统（图3），在单轴气浮转台（图4）上进行了验证。气浮转台以xPC为处理单元，俄制µFOG-6型光纤陀螺为测量单元，飞轮为执行机构。使用设计的批量MEMS陀螺系统测量转台的角速率，并在计算机上进行数据处理。

图3 批量MEMS陀螺系统Fig.3 System of multiple MEMS gyros

图4 单轴气浮转台Fig.4 Single-axis air bearing turntable

4.1 单轴气浮转台稳定控制

当气浮转台稳定控制时，在1～308 sample时，对光纤陀螺输出数据取平均，看作是转台的真实角速率，此时角速度可以将此段过程看作是高精度角速度敏感器正常的情况，即存在参考角速度，且，在这段时间里建立角速率估计误差趋势项的 SVR模型。第309～700 sample时，认为高精度角速度敏感器短时失效，但可以认为参考角速率不变，即MEMS陀螺系统进入预测校正模式，通过之前建立的SVR模型预测， 并对陀螺Kalman滤波后的结果进行补偿，消除趋势项的影响。最后，对补偿后的各陀螺数据进行了融合。下面以陀螺2、陀螺3、陀螺6为例，展示了相关数据处理的结果，如图5～图10所示。

图5 陀螺2的补偿结果Fig.5 Compensation result of gyro 2#

图6 陀螺2的补偿误差和加权系数Fig.6 Compensation errors and weighted coefficients of gyro 2#

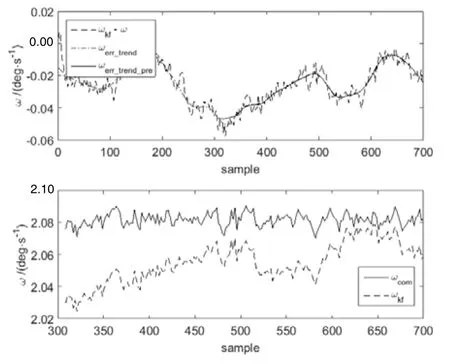
图7 陀螺3的补偿结果Fig.7 Compensation result of gyro 3#

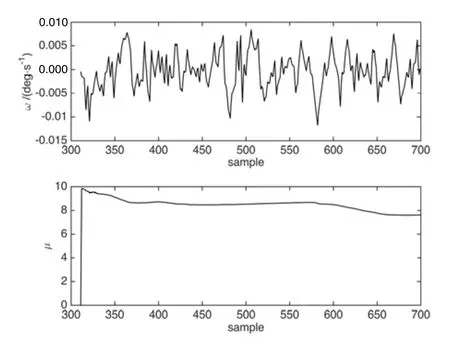
图8 陀螺3补偿误差和加权系数Fig.8 Compensation errors and weighted coefficients of gyro 3

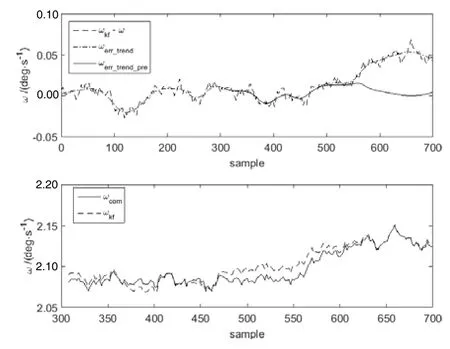
图9 陀螺6的补偿结果Fig.9 Compensation result of gyro 6#

图10 陀螺6补偿误差和加权系数Fig.10 Compensation errors and weighted coefficients of gyro 6#

4.2 结果分析

图5、图7和图9为转台稳定控制过程中基于SVR的趋势项预测补偿的结果，各图上半部分为趋势项的预测结果，下半部分为各子滤波器趋势项补偿前后的结果对比。图6、图 8和图10的上半部分为补偿误差，下半部分为各陀螺在数据融合过程中的加权系数。

图5、图7和图9分别代表了基于SVR的趋势项预测补偿算法的三类结果：一是预测与实际在某些样本点处存在偏差；二是预测精度较高；三是预测后期发散。出现这三种结果的原因在于前308个样本点建模结果的不同泛化能力，由于采用的是基于模型的预测补偿算法，因此不能保证每一个子滤波器的都可以达到较好的补偿结果。

对于这些由模型误差引起的补偿误差，本文利用各子滤波器补偿后结果的差异性，通过基于支持度融合算法予以仲裁和修正。由图6、图8和图10可以看出，融合算法对各补偿结果差异性的敏感性。由图 8中上半部分可以看出，陀螺3的补偿效果较好，其误差的方差较小，可以认为在大部分时间内，其加权系数在六个陀螺之中是较高的。但是从图6中可以看出，在第550～600个样本点时，补偿结果出现了较大的误差，因而使得其加权系数在第550～600个样本点处有所下降。同样，从图10也可以看出，由于补偿结果的发散，其第550个样本点之后的加权系数迅速下降。由此便可以看出，本文设计的融合算法对补偿误差的敏感性和对预测误差引起的个别差异较大的补偿结果抑制的有效性。从方差分析来看，未使用预测补偿算法为 3.6753×10-5，使用预测补偿算法为 1.1537×10-5。可以看出，融合算法显著降低了角速率估计值的方差。

5 结 论

本文针对多个同类 MEMS陀螺构成的卫星姿态确定系统，设计了基于ARMA模型的Kalman滤波器，根据支持度函数实时分配各个陀螺的加权系数，从而得到最优的角速率估计值。为了抑制陀螺随机误差趋势项对卫星稳定控制的不利影响，本文提出了基于SVR的趋势项预测补偿算法。半实物仿真结果表明，经过预测补偿算法融合后的角速率估计值的方差是未使用时的31.39%，显著提高了MEMS陀螺系统的测量精度。

本文提出的趋势项预测补偿算法是针对卫星稳定控制过程的，适用于卫星姿态保持阶段或匀速机动过程。因此，后续工作将考虑在卫星变速机动过程的信息融合算法。

（References）：

[1]李博文, 姚丹亚. 低成本车载 MEMS惯导导航定位方法[J]. 中国惯性技术学报, 2014, 22(6): 719-723.Li B, Yao D. Low-cost MEMS IMU navigation positioning method for land vehicle[J]. Journal of Chinese Inertial Technology, 2014, 22(6): 719-723.

[2]Abhilash M, Kumar S, Sandya S, et al. Implementation of the MEMS-based dual-axis sun sensor for nano-satellites[C]//Metrology for Aerospace (MetroAeroSpace). IEEE,2014: 190-195.

[3]王新龙, 李娜. MEMS 陀螺随机误差的建模与分析[J].北京航空航天大学学报, 2012, 38(2): 170- 174.Wang X, Li N. Error modeling and analysis for random drift of MEMS gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2):170-174.

[4]Chen M M, Gao G W. Research on MEMS gyroscope random error compensation algorithm based on ARMA model[C]//Applied Mechanics and Materials. 2014, 602-605: 891-894.

[5]Shi Y S, Gao Z F. Study on MEMS gyro signal de-noising based on improved wavelet threshold method[J]. Applied Mechanics and Materials, 2013, 433-435: 1558-1562.

[6]Yuan J, Yuan Y, Liu F, et al. An improved noise reduction algorithm based on wavelet transformation for MEMS gyroscope[J]. Frontiers of Optoelectronics, 2015, 8(4):413-418.

[7]Farahani M A, Wylie M T V, Castillo-Guerra E, et al.Reduction in the number of averages required in BOTDA sensors using wavelet denoising techniques [J]. Journal of Lightwave Technology, 2012, 30(8): 1134-1142.

[8]徐晓苏, 周峰, 张涛,等. 遗传算法优化的神经网络在SINS/GPS中的应用[J]. 中国惯性技术学报, 2015,23(3): 322-327.Xu X, Zhou F, Zhang T, et al. Application of neural network by genetic algorithm optimization in SINS/GPS[J]. Journal of Chinese Inertial Technology, 2015, 23(3):322-327.

[9]Xiao W X, Zhang H, Ma X Q. Using BP neural network and kalman filter to signal processing of MEMS inertial sensors[J]. Sensors & Transducers, 2013, 156(9), 81- 88.

[10]姜宇, 金晶, 张迎春. 基于异方差分析的多 MEMS陀螺随机误差补偿方法[J]. 宇航学报, 2012, 33(6): 776-780.Jiang Y, Jin J, Zhang Y. Compensation method for random error signals of multiple MEMS gyroscopes based on heteroscedasticity analysis[J]. Journal of Astronautics, 2012, 33(6): 776- 780.

[11]Ayat N E, Cheriet M, Remaki L, et al. KMOD-A new support vector machine kernel with moderate decreasing for pattern recognition. Application to digit image recognition[C]//Proceedings of the Sixth International Conference on Document Analysis and Recognition. IEEE,2001: 1215-1219.

Predictive compensation algorithm for trend terms of MEMS gyro random errors based on support vector regression

CHENG Yu, YE Dong, SUN Zhao-wei
(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150001, China)

In order to keep up with the development trend of low cost and fast response satellite, more and more satellites adopt such design schema as combining the MEMS (Micro Electro Mechanical System) gyro system with an information fusion method. In order to improve the precision of traditional information fusion method based on ARMA (Auto-Regression and Moving Average) model and support degree, and to inhibit the random error trend-term’s adverse influences on satellite stability control, a predictive compensation algorithm based on SVR (Support Vector Regression) is proposed. By filtering the output data of each MEMS gyro, the algorithm extracts the corresponding random error trend term. With the phase space reconstruction, the training samples are obtained and then SVR model is built for the real time compensation.The MEMS gyro system is built with low cost commercial devices, and the experimental results are carried out on a single-axis air bearing table. Experiment results show that, by applying the predictive compensation algorithm, the output data’s variance of MEMS gyro system is reduced to 31.39% of the original one,showing that the fusion precision is significantly improved.

MEMS gyro; time series; support vector machine; phase space reconstruction

V441

A

1005-6734(2016)05-0600-07

10.13695/j.cnki.12-1222/o3.2016.05.008

2016-06-28；

2016-09-18

国家自然科学基金资助项目（61603115）；中国博士后科学基金资助项目（2015M81455）；微小型航天器技术重点学科实验室开放基金资助（HIT.KLOF.MST.201501）

成雨（1990—），男，博士研究生，从事微惯性系统与信息融合算法研究。E-mail: 14B918050@hit.edu.cn

联 系 人：叶东（1985—），男，博士/讲师。E-mail: yed@hit.edu.cn