"变形"记

"变形"记

刘虎

课本中的例题是掌握数学知识和方法的重要来源.例题本身往往并不复杂，但其示范作用不可小觑.若在学习时我们能够厘清题中所蕴含的基本数学思想与方法，掌握其解决问题的本质，做到举一反三、触类旁通，无论题目如何演变，我们都可以轻松地在纷繁复杂的图形中以不变应万变.

【原题再现】（苏科版《数学》教材九（下）第110页例3）如图1，在△ABC中，AC=8，∠B= 45°，∠A=30°，求AB.

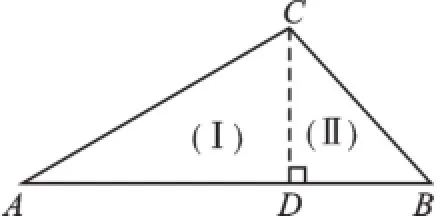
图1

【说明】本例题实质是通过对图形的分割，构造出两个特殊的直角三角形进行求解.过点C作CD⊥AB，以CD为纽带，分别在Rt△ADC和Rt△BDC中求出AD和BD的长，进而求出AB.在解直角三角形的实际问题中，有许多图形往往是由两个直角三角形的位置或条件的变换得到的，请看下面几种变形.

“变形”第一计：平移

例1如图2，在一滑梯侧面示意图中，BD∥AF，BC⊥AF于点C，DE⊥AF于点E.BC= 1.8m，BD=0.5m，∠A=45°，∠F=29°.

图2

（1）求滑道DF的长.（结果精确到0.1m）

（2）求踏梯AB底端A与滑道DF底端F的距离AF.（结果精确到0.1m）

（sin29°=0.48，cos29°=0.87，tan29°=0.55）

【分析】本题中所含Rt△ABC和Rt△FDE是由例题中的三角形Ⅰ、Ⅱ沿水平方向左右平移得到，因BC与DE本来重合，则BC=DE（也可由矩形BCED得到），可分别求DF、EF、AC.

解：（1）在Rt△DEF中，

∠DEF=90°，DE=BC=1.8，∠F=29°.

在Rt△ABC中，∠ACB=90°.

由∠A=∠ABC=45°得AC=BC=1.8.

又∵CE=BD=0.5，

∴AF=AC+CE+EF=1.8+0.5+3.27=5.6.

答：DF长约为3.8m，AF长约为5.6m.

“变形”第二计：翻折

例2（2015·湖南娄底）为了安全，请勿超速.如图3，一条公路建成通车，在某直线路段MN限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由（.参考数据：2≈1.41，3≈1.73）

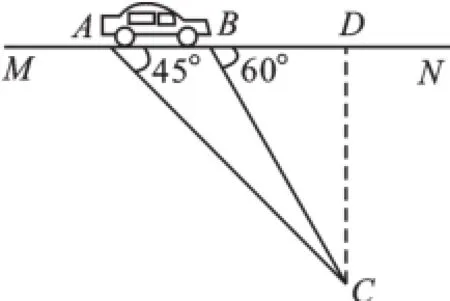
图3

【分析】Rt△BDC可看成例题中的三角形Ⅱ沿着高CD翻折，再把整个图形沿AB翻折后得到，解Rt△BDC和Rt△ADC得BD、CD、AD.（提示：例题和本题模型结合，还可以设计在无图条件下，已知两边和第三边上的高求第三边长，注意两解.）

解：过点C作CD⊥MN，垂足为D.

∵CD⊥MN，∠DBC=60°，∴∠BCD=30°，

∵CD⊥MN，∠CAD=45°，

∴∠DCA=∠DAC=45°，

∴AD=DC=173，AB=173-100=73，

“变形”第三计：旋转

例3如图4，甲、乙两数学兴趣小组测山CD的高度.甲小组在地面A处测量，乙小组在上坡B处测量，AB=200m.甲小组测得山顶D的仰角为45°，山坡B处的仰角为30°；乙小组测得山顶D的仰角为58°.求山CD的高度（.结果保留一位小数）（参考数据：tan58°≈1.60，≈1.732）

图4

【分析】在构造直角三角形后，△BDF其实是由课本例题中的三角形Ⅱ绕点C逆时针旋转90°得到（只是表示位置变换，BE、BF不一定相等）.设BF=x，根据边角关系，在△ABE、△BDF中求BE、AE、DF的值及表达式，因AC= DC列出方程求解.

解：过B作BE⊥AC，BF⊥DC，E、F为垂足，在矩形BECF中，BF=EC，BE=FC.

设BF=x，则EC=x.在Rt△ABE中，

BE=AB·sin∠BAE=200·sin30°=100，

DF=BF·tan∠DBF=x·tan58°≈1.60x，

在Rt△DAC中，∠DAC=45°，

∴CA=CD，即AE+EC=DF+FC，

∴CD=CA=173.2+122.0=295.2.

答：山高约为295.2m.

“变形”第四计：翻折和平移

例4（2016·江苏淮安）如图5，小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到点D处，测得∠BDF=60°.

若直线AB与EF之间的距离为60米，求A、B两点之间的距离.

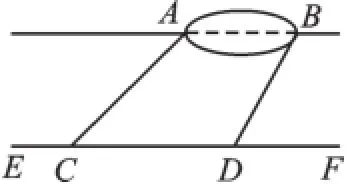
图5

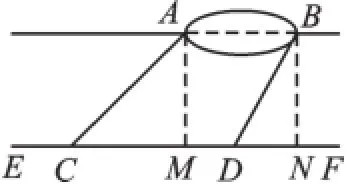
图6

【分析】如图6，过点A、B分别作AM⊥EF、BN⊥EF得到两个直角三角形，会发现该图相当于例题中的三角形Ⅱ沿高CD翻折后再平移得到，由于AB=MN=CN-CM，所以求得CM、CN的长即可解决问题.

解：过点A作AM⊥EF于点M，过点B作BN⊥EF于点N，由题意可得，AM=BN=60（米），CD=100（米），∠ACF=45°，∠BDF=60°，

∴在Rt△ACM中，CM=AM=60，

在Rt△BDN中，DN=

“变形”第五计：翻折并扩大（缩小）

例5如图7，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A、C两点测得该塔顶端F的仰角分别为α和β，矩形建筑物宽度AD=20m，高度DC=33m.求：

（1）试用α和β的三角函数值表示线段CG的长；

（2）如果α=48°，β=65°，请求出信号发射塔顶端到地面的高度FG的值.（结果精确到1m）

图7

（参考数据：sin48°=0.7，cos48°=0.7，tan48° =1.1，sin65°=0.9，cos65°=0.4，tan65°=2.1）

【分析】图中Rt△FCG可看成例题中的三角形Ⅱ沿高CD向左翻折，再扩大后得到的，分别解Rt△FAE和Rt△FCG即可.设CG=x（m），用x表示EF、FG，综合后发现FG有两种表达式，进而用方程求解.

解：（1）设CG=xm，由图可知：

EF=（x+20）tanα，FG=xtanβ，由EF+EG= FG得：

（x+20）tanα+33=xtanβ，

则FG=xtanβ=55×2.1=115.5≈116.

答：信号发射塔顶端到地面的高度约是116m.

在中考试题中，关于解直角三角形的问题，大多是由我们学习过的基本图形演变而来的，只不过设置在不同的背景下，将图形和条件做适当的变化，进行乔装打扮而已.解答此类题目时，只要大家能主动联想熟悉的基本模型，看清其演变的方式，抓住直角三角形，找准线段之间的关系，就很容易做出解答了.

（作者单位：江苏省东台市富安中学）