长三角交通一体化对地方经济发展的影响研究

郭岚萍，凤飞翔，赵 旭

(1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 金融学院，安徽 蚌埠 233030)



长三角交通一体化对地方经济发展的影响研究

郭岚萍，凤飞翔1，赵 旭2

(1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 金融学院，安徽 蚌埠 233030)

长三角交通一体化自大规模投入建设以来，已初步达到区域内交通、经济一体化。本文利用长三角地区2005-2014年交通和经济的相关数据，建立引力模型分析交通一体化对长三角地区贸易交易量的影响分析；利用客货运量与8个主要经济指标建立关联度排序模型，定量分析上海对长三角都市圈的经济影响。

长三角；交通一体化；引力模型

0 引言

长三角交通一体化自90年代大规模投入建设以来，现已初具规模，逐步形成长三角都市圈。上海作为整体发展的中心，起着主导作用，上海将自己的经济影响力辐射于整个长三角都市圈的16个城市。交通一体化的形成，直接促进城市之间的贸易往来，缩短地区间的时空距离，为经济促进、资源互换、贸易往来建立更快、更短的桥梁。本文以2005-2014年的经济类和交通类数据为基础，通过建立数学模型，来分析上海推进长三角交通一体化的10年中，交通一体化对长三角都市贸易圈的促进作用和长三角都市圈的经济影响，挖掘长三角地区的经济潜力，为长三角区域经济提供巨大的发展空间。

1 基于引力模型对长三角贸易交易量的影响分析

1.1 建模思路

通过查阅长三角地区16个城市的统计年鉴和长三角地区经济发展报告，获得2005-2014年长三角地区客货运量和人均GDP的相关数据；利用百度地图[1]，得到长三角地区16个城市之间的城际距离，构造距离矩阵。

将2005-2014年长三角地区客货运量的数据作为交通基础设施面板数据，以公路、铁路、航空交通运输方式的客货运量为贸易流量指标；引入解释变量：人均GDP和城际间距离。分析长三角交通一体化对长三角地区的贸易交易量是否有促进作用。

1.2 模型建立

引力模型[2]是通过地区间贸易来分析区域一体化的基本理论，是贸易理论中最成功的经验模型，反映了两地间的贸易状况与这两地间的经济规模成正比，与两地间的距离成反比[3]，具体模型为：

lnTradeij=α0+α1lnGDPi+α2lnGDPj+α3lnDisij+εij

其中：Tradeij表示地区i向地区j的出口贸易；GDPi、GDPj为地区i和地区j的GDP；Disij表示地区i与j之间城际距离；εij为残差项，包含影响城际间贸易的其他因素。

由于贸易状况影响产业空间集聚，进而会影响经济增长。因此，为了观察地区经济活动的密集程度，本文选取交通运输方式的客货运量(YL)代替式Tradeij，以人均GDP(PGDP)代表GDP，将地区i与j之间城际距离用矩阵ω来代替，用其方程为：

lnYLij=α0+α1ωlnYLij+α2lnPGDPi+α3lnPGDPj+εij=α0+α1ωlnYLij+α2lnPGDPi+α3ωlnPGDPi+εij

其中，ωlnYLij表示城际距离对客货运量的交互影响；ωlnPGDPi表示城际距离对人均GDP的交互影响。

1.3 模型求解及检验

利用STATA软件[4]进行参数估计，为了便于命令输入，将模型简化：

y=α0+α1x1+α2x2+α3x3+εij

其中y表示lnYLij；x1表示ωlnYLij；x2表示lnPGDPi；x3表示ωlnPGDPi

因为lnYLij与ωlnYLij存在共线性，x1是内生变量，因此要引入工具变量Y，为lnYLij的滞后两阶。工具变量[5]的引入并没有改变原模型，只是在原模型的参数估计过程中用工具变量“替代”随机解释变量。

1) 广义矩估计—gmm估计

命令：ivregress gmm y x2 x3 (x1=Y)；est store gmm

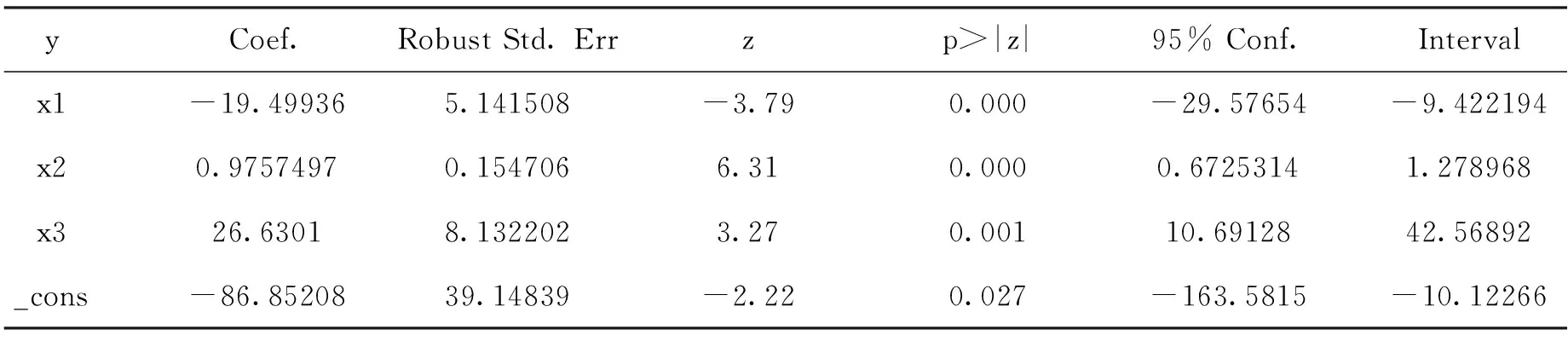
表1 gmm估计参数结果

由估计结果可得到模型方程为：

lnYLij=-86.85-19.50ωlnYLij+0.98lnPGDPi+26.63ωlnPGDPi+εij

2)两阶段最小二乘法估计—2sls估计

命令：ivregress 2sls y x2 x3 (x1=Y)；est store 2sls

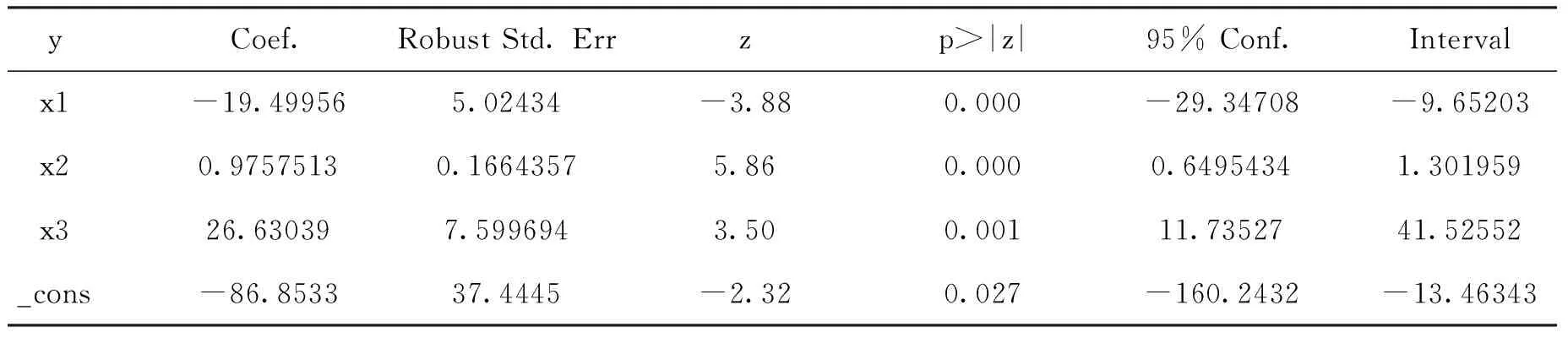
表2 2sls估计参数结果

由估计结果可得到模型方程为：

lnYLij=-86.85-19.50ωlnYLij+0.98lnPGDPi+26.63ωlnPGDPi+εij

3)有限信息极大似然估计—liml估计

命令：ivregress liml y x2 x3 (x1=Y)；est store liml

表3 liml估计参数结果

由估计结果可得到模型方程为：

lnYLij=-86.85-19.50ωlnYLij+0.98lnPGDPi+26.63ωlnPGDPi+εij

4)模型的显著性检验

命令：esttab gmm 2sls liml b(%12.6f) se star(* 0.1 ** 0.05 *** 0.01)

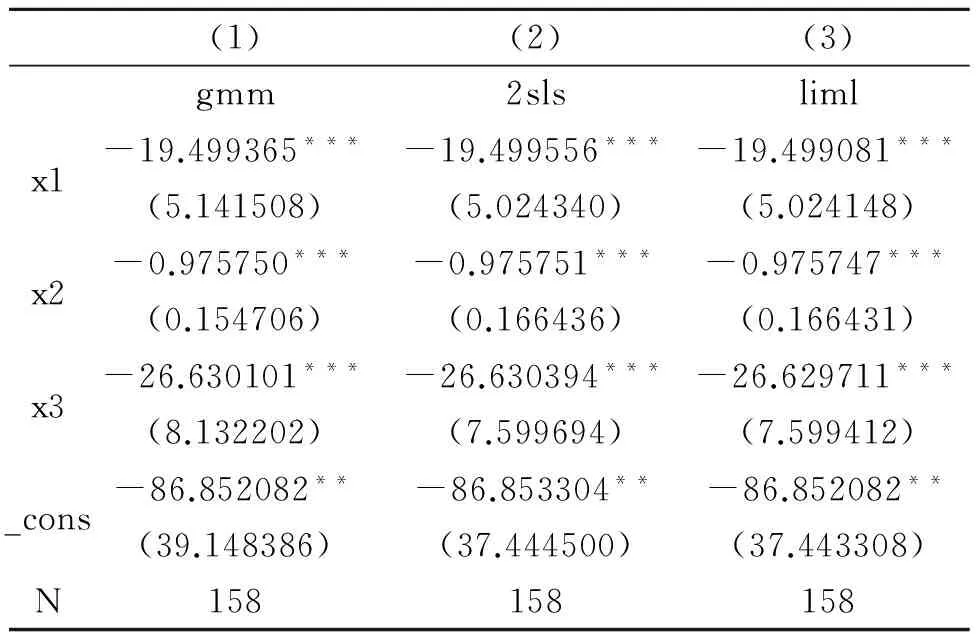
表4 模型的显著性检验

注：Standard errors in parentheses*P<0.1**Pp<0.05***P<0.01

由显著性检验结果p<0.01和p<0.05可知，三种模型均通过显著性检验。

1.4 结果分析

由α2>0，α3>0可知，长三角交通一体化促进了长三角地区16个城市的贸易交易量，进而带动人均GDP的提高；由α1<0可知，城际之间距离与客货运量呈负相关，表明两地间的贸易交易量与两地间的距离成反比，说明交通一体化还未完全实现贸易互通，仍有很大发展空间，要继续推进长三角多中心城市体系的逐步形成[6]。综合分析，上海推动长三角交通一体化对长三角地区的贸易交易量有正向促进作用。

2 基于关联度排序模型对长三角经济影响分析

2.1 建模思路

通过查阅长三角地区16个城市的统计年鉴和长三角地区经济发展报告，获得2005-2014年长三角地区的8个主要经济指标的相关数据。8个经济指标分别为GDP、人均GDP、财政总收入、CPI、工业产值、零售总额、外贸进出口总额和旅游收入。将长三角地区客货运量作为交通指标，结合8个主要经济指标建立关联度排序模型，对交通一体化和各经济指标进行关联度分析，定量分析上海推动交通一体化后，在其所在的长三角经济圈的经济影响力。

2.2 模型建立

1)确定参考数列和比较数列

参考数列：2005-2014年长三角地区16个城市的客货运量，记做x0；

比较数列：2005-2014年长三角地区16个城市的8个经济指标数据，记做xi(i=1,2,……7,8)。

2)数据标准化处理

由于各因素量纲不一致，需将原始数据按照下列公式进行标准化处理。

3)计算两极最大差与最小差

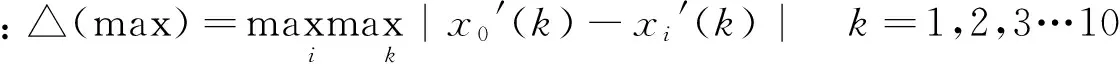
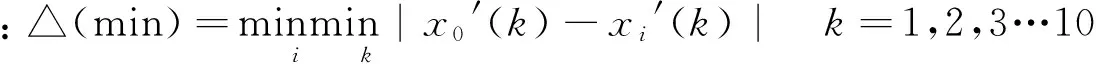
4)计算关联系数

其中：ρ为分辨系数，用来削弱Δ(max)过大而使关联系数失真的影响。人为引入这个系数是为了提高关联系数之间的差异显著性。这里取ρ=0.5

2.3 模型求解

利用MATLAB软件编程进行求解，得出结果如下：

γ1=0.7117，γ2=0.7284，γ3=0.7148，γ4=0.7213

γ5=0.7364，γ6=0.7043，γ7=0.7633，γ8=0.8574

将结果进行排序，得到交通一体化与各经济指标的关联序依次为：

γ8(旅游收入)>γ7(外贸进出口总额)>γ5(工业产值) >γ2(人均GDP) >γ4(CPI) > γ3(财政总收入) >γ1(GDP)>γ6(零售总额)。

2.4 结果分析

依照关联分析原则[7]，关联度大的与参考数列的关系密切，关联度小的数列与参考数列的关系疏远，因此可知上海推动长三角交通一体化后对长三角的经济影响最大的是旅游收入，可见上海促使交通便利刺激了长三角地区旅游业的发展；其次是外贸进出口总额、工业产值、人均GDP和CPI，可见上海促使交通便利刺激了长三角地区进出口贸易和工业生产，提高了人们的生活水平和消费水平；对财政总收入、GDP和零售总额影响较小。

3 结论

1.通过引力模型，我们发现长三角交通一体化促进了长三角地区16个城市的贸易交易量，进而带动人均GDP的提高；长三角地区两个城市间的贸易交易量与两地间的距离成反比，说明交通一体化还未完全实现贸易互通，推进长三角都市圈形成的任务任重而道远。但总体来看，上海推动长三角交通一体化对长三角地区的贸易交易量有正向促进作用。

2.通过关联度排序模型，我们发现上海推动长三角交通一体化后对长三角地区的旅游收入影响最大，可见长三角交通一体化使得交通便利，刺激了长三角地区旅游业的发展；影响由大到小依次是外贸进出口总额、工业产值、人均GDP和CPI，可见长三角交通一体化促进了长三角地区进出口贸易和工业生产，提高了人们的生活水平和消费水平。

[1]姜启源,谢金星,叶俊.数学模型(第四版)[M].北京:高等教育出版社,2011.

[2]刘育红,王曦.“新丝绸之路”经济带交通基础设施与区域经济一体化[J].西安交通大学学报,2014,34(2):43-80.

[3]郝景芳.基于面板数据引力模型的中国对外贸易研究[D].北京:清华大学,2012.

[4]周广肃.Stata统计分析与应用(第二版)[M].北京:机械工业出版社,2015.

[5]李子奈,潘文卿.计量经济学(第三版)[M].北京:高等教育出版社,2010.

[6]霍妮.城际轨道交通对城市群一体化发展的影响研究[D].广州:暨南大学,2014.

Initial Analysis on the Economic Impact of Transport Integration in Yangtze River Delta

GUO Lan-ping1，FENG Fei-xiang1，ZHAO Xu2

(1.Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, Anhui 233030，China; 2.Financial Institute, Anhui University of Finance and Economics, Bengbu, Anhui 233030，China)

Transportation integration in Yangtze River Delta has been initially to achieve transportation and economic integration since the scale of investment in construction. The paper uses the data of traffic and economy from 2005 to 2014 in Yangtze River Delta, building of model of gravity to analyze the influence of trade volume in the Yangtze River Delta. Besides we make use of passenger and freight volume and 8 major economic indicators to establish the model of relational degree taxis, in order to quantitative analysis of the economic impact of Shanghai in Yangtze Delta Metropolitan Area.

transport integration in Yangtze River Delta; economic impact; gravity model

2016-05-24

郭岚萍(1995- )，女，浙江杭州人，安徽财经大学统计与应用数学学院。主要研究方向：数学统计。

F127;F207

A

1673-6125(2016)03-0056-04