介质折射率对对称结构光子晶体内部局域电场的调制
2016-12-22唐秀福罗家昌卢逢旺刘俊
唐秀福 罗家昌 卢逢旺 刘俊
(河池学院 物理与机电工程学院, 广西 宜州 546300)
介质折射率对对称结构光子晶体内部局域电场的调制
唐秀福 罗家昌 卢逢旺 刘俊
(河池学院 物理与机电工程学院, 广西 宜州 546300)
利用传输矩阵法理论,研究介质折射率对镜像对称结构一维光子晶体内部局域电场的调制,揭示介质折射率的变化与内部局域电场强度变化之间的规律,结果表明:对于对称结构光子晶体(AB)5(BA)5,随着介质A的折射率或A、B介质的折射率比值的增大,内部局域电场降低;随着介质B的折射率增大,内部局域电场增强。对于光子晶体(AB)5(BA)2(AB)2(BA)5,随着介质A、B的折射率之差的绝对值增大,光子晶体内部局域电场增强,对光在光子晶体中传播的局域限制作用增大,光子晶体的分立透射峰也越来越精细。
光子晶体;折射率;局域电场;调制;对称结构
0 引言
光子晶体是在1987年由S.John和E.Yablonovitch分别独立提出,是由不同折射率的介质周期性排列而成的人工微结构[1-2]。光子晶体在半个多世纪的发展中体现出做为光子通信领域材料的卓越优势,光子晶体根本的特性是具有光子禁带和光子局域。光子禁带是指入射到光子晶体的光存在一定的频率范围,在这一特定范围内的电磁波,不能在光子晶体中传播;光子局域是指在光子晶体中传播的光被局域于某个位置,这个位置中的光由于被局域限制,会产生很强的局域光子态或很强的局域电场,这些光子态可以通过隧穿的方式通过光子晶体,形成精细的透射峰[3-8]。研究结果已经表明,合理的引入缺陷也可以增强缺陷位置处的光子态密度,即增强缺陷位置处的局域电场,从而增强该位置的自发辐射,获得需要的精细的分立缺陷模[8-12]。这种机制对光子晶体设计和制备光学滤波器件具有巨大的应用前景。
可见,光子晶体宏观上的透射峰(或缺陷模)与光子晶体内部的局域电场强度的强弱关系密切,如何通过宏观的结构参数调制来调节内部局域电场的强弱,以获得最终需要的透射特性(分立透射谱),是光子晶体研究所必需解决的问题之一[3-4,13-14]。当前,对各种光子晶体模型的透射谱研究文献已经很多,研究光子晶体内部电场的文献也不少,但对于折射率调制光子晶体内部局域电场的研究文献还很少见到,尤其是介质折射率对对称结构光子晶体内部局域电场的影响研究还未见。基于这个思路,本文在构造镜像对称结构光子晶体模型的基础上,通过介质折射率的几种变化,计算模拟出光子晶体的内部局域电场,并分析研究介质折射率变化与内部局域电场变化之间的关系,然后以实例进行验证这种机制对光子晶体透射能带谱的影响规律。此举将为光子晶体的理论研究的实际设计提供理论参考。
1 研究方法和模型
鉴于计算和研究的主要对象是一维光子晶体的内部局域电场和透射谱,本文研究方法采用本领域广泛使用且成熟、直观的传输矩阵法[3-14],该研究方法的理论推导演算已经有诸多文献报道,再此不做复述。研究的模型为镜像对称结构(AB)5(BA)5和(AB)5(BA)2(AB)2(BA)5,即镜像对称结构模型光子晶体由A、B两种不同的介质薄膜周期性排列而成。模型中下标“5”是排列周期数,A、B介质的折射率初始值为nA=1.38、nB=2.35,在计算中可根据研究需要对折射率值进行调节。A、B两介质层薄膜的物理厚度分别为dA=281 nm,dB=165 nm。
2 研究结果与分析
2.1 折射率对(AB)5(BA)5内部局域电场强度的调制
2.1.1nA对内部局域电场的影响

图1 nA对局域电场的影响图 图2 nB对局域电场的影响图 图3 nA/nB对局域电场的影响图
首先,保持光子晶体(AB)5(BA)5的其他参数不变,并固定B介质的折射率nB=2.35,以0.02为步长,逐渐增大A介质层的折射率,即取nA=1.38、1.40、1.42、1.44、1.46,计算模拟出光子晶体的内部局域电场,如图1所示。图中纵坐标以相对值表示│E/E0│表示局域电场的大小。
从图1可见,随着A介质层折射率nA增大,光子晶体(AB)5(BA)5的内部局域电场减弱,nA=1.38、1.40、1.42、1.44、1.46时,内部局域电场最大值│E/E0│max分别为6.094、5.668、5.272、4.918和4.588,即单向减弱,如图1(a)~(e)所示。
2.1.2nB对内部局域电场的影响
继续保持光子晶体(AB)5(BA)5的其他参数不变,并固定A介质的折射率nA=1.38,以0.02为步长,逐渐增大B介质层的折射率,即取nB=2.35、2.37、2.39、2.41、2.43,计算模拟出光子晶体的内部局域电场,如图2所示。
从图2可得,随着B介质层折射率nB增大,光子晶体(AB)5(BA)5的内部局域电场增强,nB=2.35、2.37、2.39、2.41、2.43时,内部局域电场最大值│E/E0│max分别为6.094、6.303、6.518、6.736和6.960,即单向增大,如图2(a)~(e)所示。
2.1.3nA/nB对内部局域电场的影响
保持光子晶体(AB)5(BA)5的其他参数不变,以0.02为步长,然后逐渐增大介质A、B折射的比值nA/nB,即取nA/nB=0.587、0.607、0.627、0.647、0.667,计算模拟出光子晶体的内部局域电场,如图3所示。
从图3可得,随着A、B介质层折射率比值nA/nB增大,光子晶体(AB)5(BA)5的内部局域电场减弱,nA/nB=0.587、0.607、0.627、0.647、0.667时,内部局域电场最大值│E/E0│max分别为6.094、5.296、4.758、4.109、3.648,即单向减弱,如图3(a)~(e)所示。
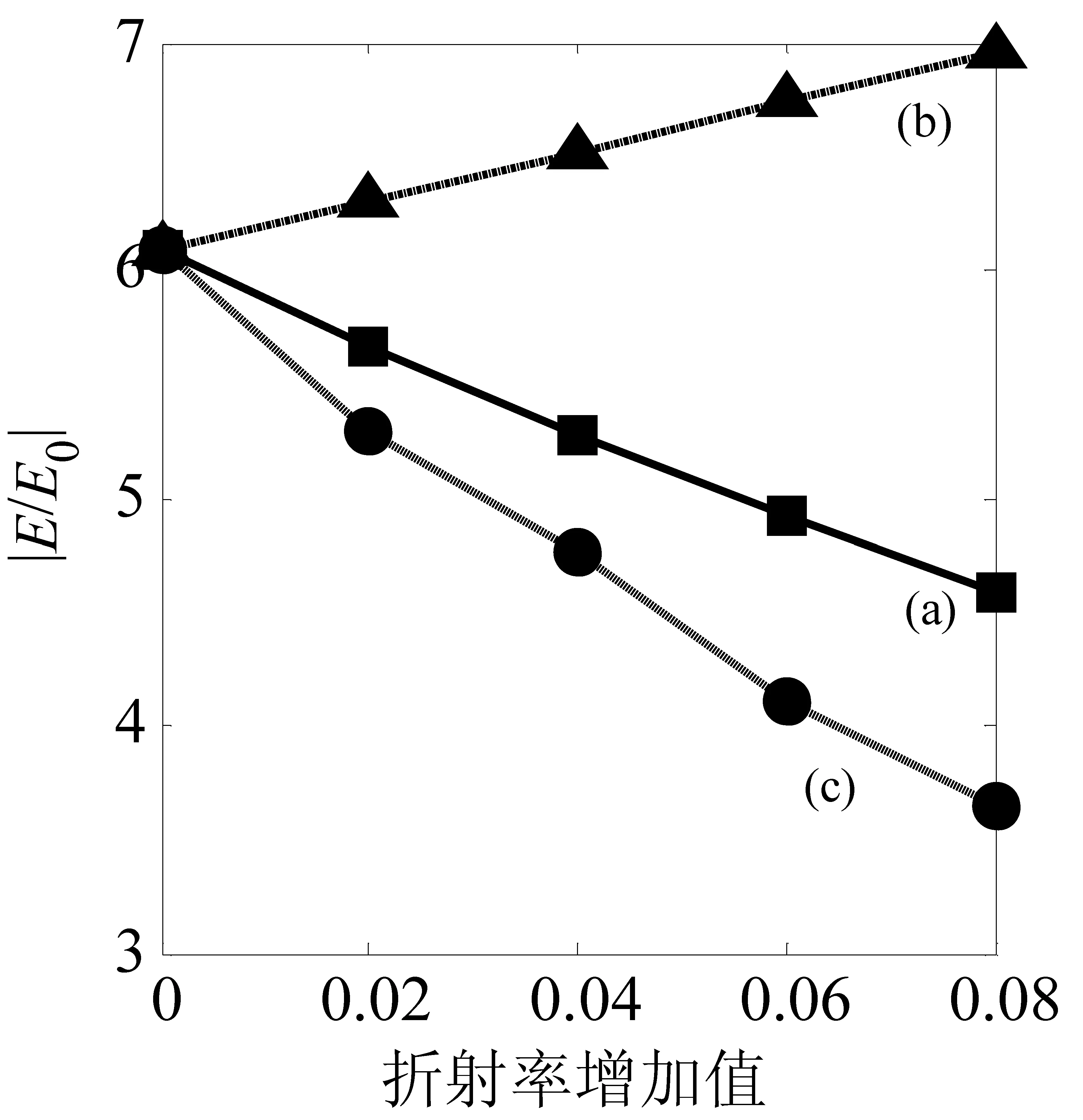
图4 折射率对局域电场的影响曲线
进一步地,以介质折射率nA、nB和nA/nB为横坐标,以光子晶体内部局域电场最大值│E/E0│max为纵坐标作图,观察三者对内部局域电场的调制规律,如图4所示。图4中带方格的实线(a)是nA依次增大0.02时内部局域电场最大值的变化曲线,带三角形的折线(b)是nB依次增大0.02时内部局域电场最大值的变化曲线,带圆圈的实线(c)是nA/nB依次增大0.02时内部局域电场最大值的变化曲线。从图4中可看出,三者变化对光子晶体的内部局域电场的影响接近于线性变化,尤其是当介质A或介质B的折射率独自增加时,局域电场的减小或增强已经趋近于线性变化,这对调制机制的设计非常有利。
以上是在nA
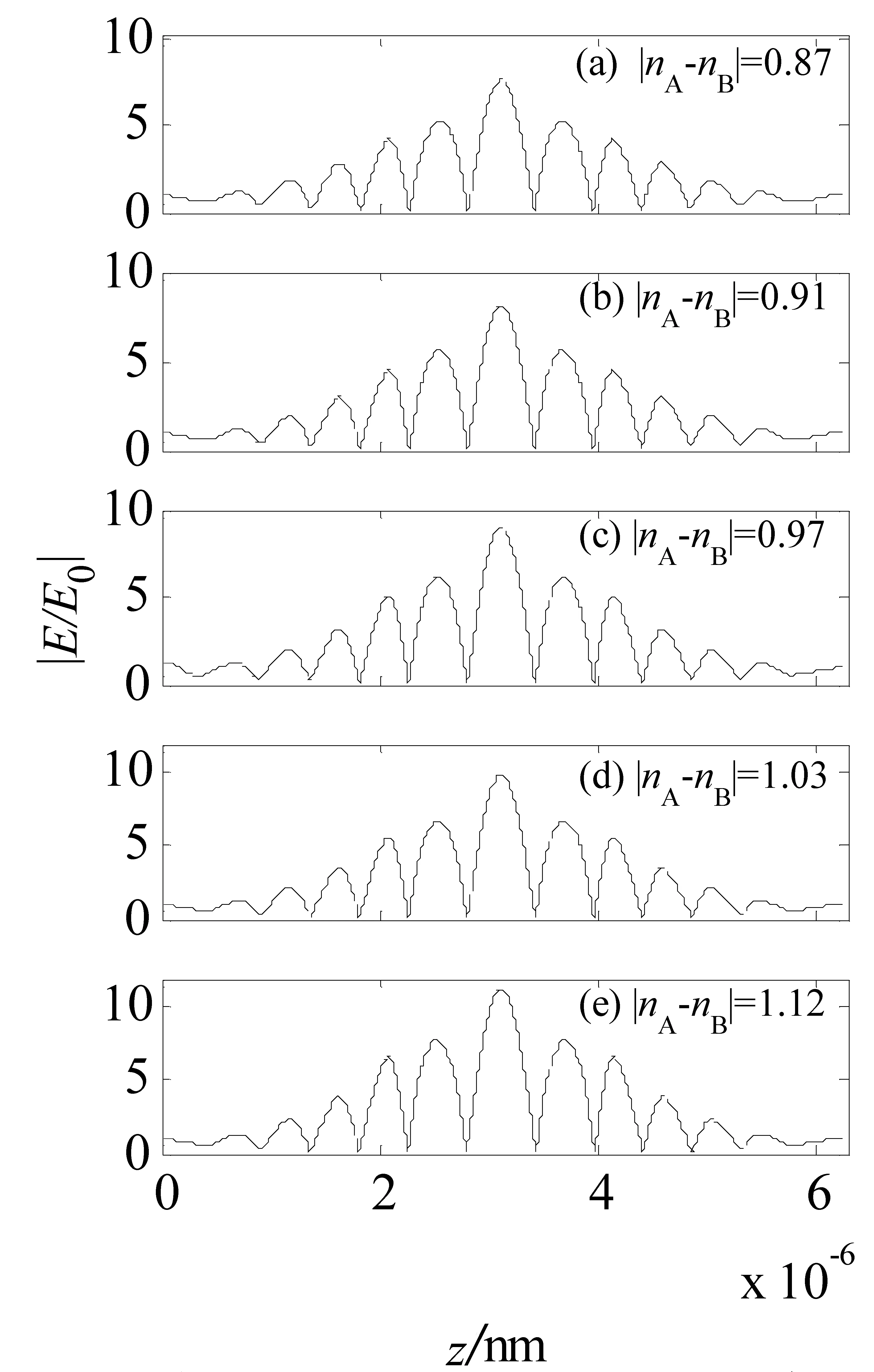
图5 │nA-nB│对局域电场的影响
综合计算结果,可见,对于对称结构光子晶体(AB)5(BA)5,当高折射率介质的折射率越大,或低折射率介质的折射率越低,或两介质的折射率差值越大时,光子晶体的内部局域电场越强。这个规律对于其他对称结构光子晶体是否也一样的呢,以对称结构光子晶体模型(AB)5(BA)2(AB)2(BA)5进行验证研究。
2.2 介质折射率对(AB)5(BA)2(AB)2(BA)5内部局域电场的调制
为了验证2.1计算发现的现象和得出的推论,构造对称结构光子晶体模型(AB)5(BA)2(AB)2(BA)5,本模型的结构参数初始值与(AB)5(BA)5模型相同。验证研究的方法是依次增大│nA-nB│的值,然后分别计算模拟出这些│nA-nB│值情况下光子晶体内部的局域电场。│nA-nB│的取值如下:
(a)当nA=1.38,nB=2.25,│nA-nB│=0.87;
(b)当nA=1.38,nB=2.29,│nA-nB│=0.91;
(c)当nA=1.38,nB=2.35,│nA-nB│=0.97;
(d)当nA=1.38,nB=2.41,│nA-nB│=1.03;
(e)当nA=1.38,nB=2.50,│nA-nB│=1.12。
通过计算模拟,结果如图5所示。从图中可以看到,随着A、B介质折射率差值的绝对值│nA-nB│的增大,光子晶体(AB)5(BA)2(AB)2(BA)5内部局域电场明显增强。当│nA-nB│=0.87、0.91、0.97、1.03、1.12时,光子晶体内部局域电场的最大值│E/E0│max分别为7.561、8.136、8.952、9.930、11.30。可见,验证的结果与2.1的推论相符。此结果表明,当镜像对称结构光子的高低折射率介质的折射率之差越大时,光子晶体内部局域电场就越大,亦即光子晶体对传播到其中的光的局域限制作用就越强,那么光要通过光子晶体就越难,在宏观上体现为越来越精细的分立透射峰。
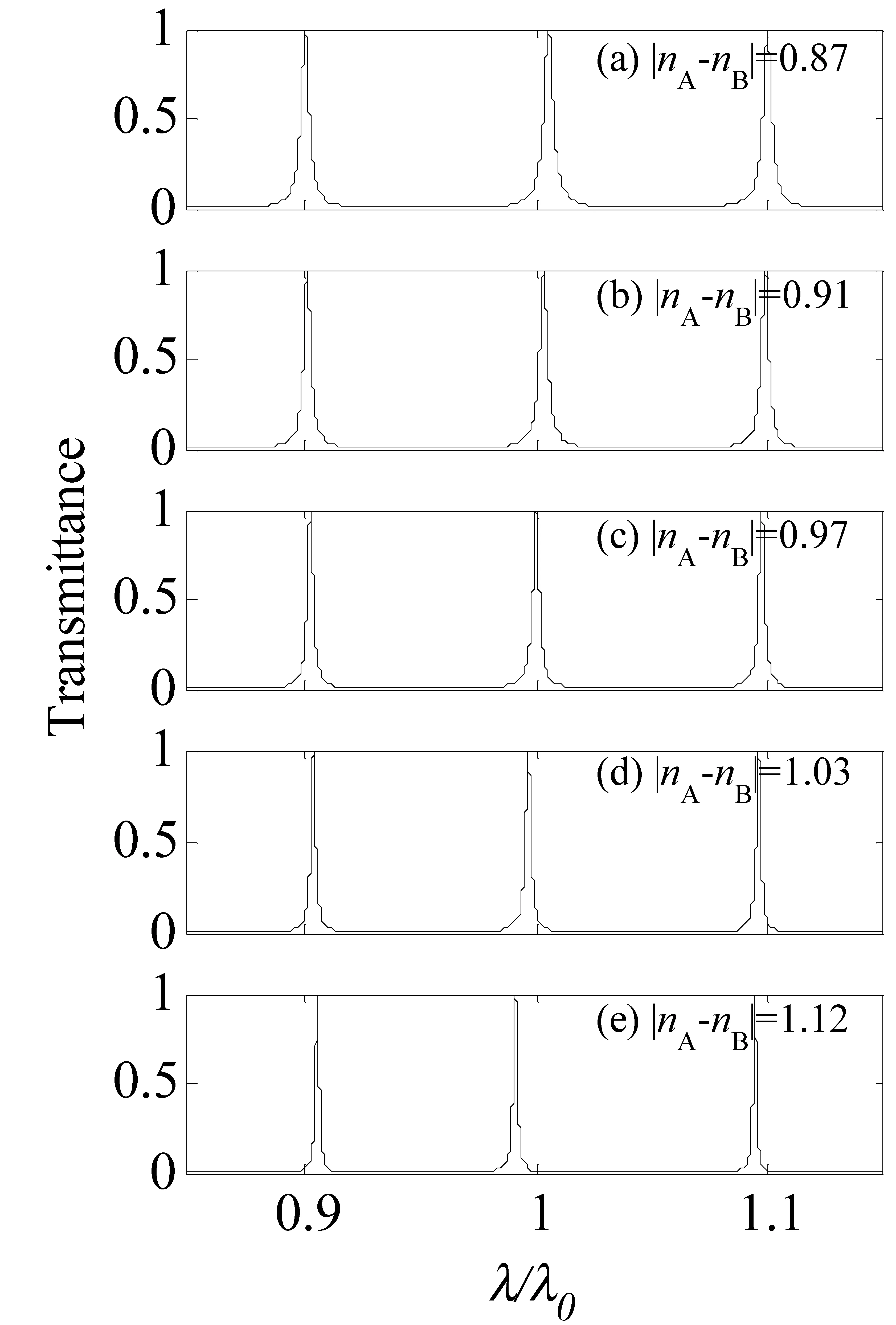
图6 │nA-nB│对透射谱的影响
进一步地,我们计算模拟出在不同│nA-nB│值情况下光子晶体(AB)5(BA)2(AB)2(BA)5的透射谱,如图6所示。从图6可见,当│nA-nB│逐渐增大时,透射谱中的3条分立透射峰的带宽越来越窄,并且3条透射峰具有向对称中心移动的趋势。这充分验证了宏观上随着│nA-nB│增大,对称结构光子晶体微观内部局域电场得到加强,最终又表现为宏观上更加精细的分立透射峰。另外,随着│nA-nB│增大,透射谱中的分立透射峰向中心移动,也验证了图1~图3和图5中,结构中心内部局域电场最强的现象。
3 结论
利用传输矩阵法理论,通过计算机编程计算模拟,研究介质折射率对对称结构光子晶体内部局域电场的调制规律,得出以下结论。
介质折射率可以有效调节对称结构光子晶体的内部局域电场,最终达到调制透射谱中分立透射峰带宽的目的。当对称结构光子晶体的高折射率介质的折射率越大,或低折射率介质的折射率越低,或是高低折射率介质的折射差值越大时,光子晶体内部局域电场就越强,光子晶体对光子的局域限制作用也越强,则光子晶体透射谱中的分立透射峰就越精细。
介质折射率对对称结构光子晶体内部局域电场强度进行调制,进而影响透射谱中分立透射峰带宽的规律,对光子晶体的理论研究和光学滤波器件的设计等具有一定的理论参考意义。
[1]Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics[J].Phys.Rev.Lett.,1987,58(20):2059-2061.
[2]ohn S. Strong localization of photons in certain disordered dielectric superlattices[J].Phys.Rev.Lett.,1987,58(23):2486-2489.
[3]苏安,高英俊.双重势垒一维光子晶体量子阱的光传输特性研究[J].物理学报,2012,61(23):234208.
[4]苏安,高英俊,蒙成举.双重势垒一维光子晶体量子阱内部局域电场分布[J].光子学报,2014,43(2):0216002.
[5]苏安,蒙成举,高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器[J].中国激光,2013,40(10):1006001.
[6]唐秀福.光子晶体研究方法对比与实例分析[J].河池学院学报,2015,35(2):45-49.
[7]唐秀福.周期数对双周期对称结构光子晶体透射谱的调制[J].河池学院学报,2016,36(2):48-52.
[8]苏安,蒙成举,高英俊.激活性杂质对光子晶体量子阱滤波器特性的调制[J].中国激光,2014,41(3):0306001.
[9]韦吉爵,苏安,唐秀福,等.缺陷对一维光子晶体滤波性能的调制[J].红外与激光工程,2015,44(S):168-172.
[10]潘继环,苏安,唐秀福,等.缺陷奇偶性对光子晶体光传输特性的影响[J].激光与红外,2015,45(6):706-709.
[11]韦吉爵,李忠海,莫传文,等.两种因素对光子晶体缺陷模的影响[J].河池学院学报,2015,35(2):40-44.
[12]苏安,白书琼,陈颖川,等.缺陷对对称结构光子晶体透射谱的影响[J].河池学院学报,2016,36(2):34-39.
[13]苏安,覃宗定,高英俊.镜像对称结构一维光量子阱的光传输特性[J].激光与红外,2011,41(8):889-893.
[14]苏安.对称结构一维三元光子晶体的透射谱和电场分布[J].西南大学学报(自然科学版),2011,33(7):26-30.
[责任编辑 刘景平]
Modulation Effect of Localized Electric Field from Index of Refraction in Photonic Crystals with Symmetry Structure
TANG Xiufu, LUO Jiachang, LU Fengwang, LIU Jun
(School of Physics and Mechanical & Electronic Engineering, Hechi University,Yizhou, Guangxi 546300, China)
Localized electric field affected by index of refraction in the one-dimensional photonic crystals with symmetry structure is studied by using the transfer matrix method to reveal the law of between the change of index of refraction and the change of the strength of localized electric field. The results show that: in the photonic crystals with symmetry structure as (AB)5(BA)5,when the refractive index of the medium A increases the localized electric field will become weaker. When the refractive index of ratio A and B increases, the localized electric field will be weaker. When the refractive index of the medium B increases the localized electric field will be stronger. In the photonic crystals with symmetry structure as (AB)5(BA)2(AB)2(BA)5, the absolute value of the difference between the refractive index of medium A, B increases, the Localized Electric Field will be stronger, and the transmission spectrum will be narrower. This paper will provide theoretical reference for the design of new photonic crystal optical devices such as optical filter, optical switch and so on.
photonic crystal; index of refraction; localized electric field; modulation effect; symmetry structure
O431
A
1672-9021(2016)05-0054-05
唐秀福(1985-),男(壮族),广西都安人,河池学院物理与机电工程学院讲师,主要研究方向:光子晶体理论和特性。
广西高校科学技术研究基金资助项目(KY2015YB258,KY2016LX287);河池学院青年基金资助课题(XJ2015QN007);广西区级大学生创新创业训练计划项目(201610605065)。
2016-09-05
