基于三种GM(1,1)的BGA焊点健康预测
2016-12-22张国礼王和明潘克战
张国礼,王和明,潘克战
(空军工程大学 防空反导学院,陕西 西安 710051)
基于三种GM(1,1)的BGA焊点健康预测
张国礼,王和明,潘克战
(空军工程大学 防空反导学院,陕西 西安 710051)
针对球形封装焊点健康预测过程中遇到的数据样本少、无明显变化规律、焊点失效过程难以预测等难题,引入灰色系统理论,建立差分、均值、离散三种1阶1变量灰色模型,并对焊点后期健康状况进行预测。仿真结果表明:三种灰色模型都可以实现球形封装焊点的健康预测,预测值与实测值基本吻合,均值灰色模型的预测结果好于其它两种模型。
灰色模型;球形封装;健康预测
0 引言
随着电子产业的蓬勃发展,BGA(Ball Grid Array)封装的芯片在航空航天设备中的应用越来越广泛,因此其使用过程中焊点的健康一直是人们关注的焦点[1-4]。由于监测困难、监测周期长、一旦失效甚至有可能引发不可挽回的灾难性损失,所以对焊点的健康进行预测就显的尤为重要。
概率统计、模糊数学和灰色系统理论是三种最常用的健康预测研究方法,其研究对象都具有某种不确定性。概率统计研究的是“随机不确定”现象,其出发点是大样本,并要求对象服从某种典型分布。模糊数学着重研究“认知不确定”问题,主要是凭经验借助于隶属函数进行处理。灰色系统理论着重研究概率统计、模糊数学所难以解决的“小样本”、“贫信息”等不确定性问题,因此适用于BGA焊点的健康预测。
1 灰色系统理论
20世纪80年代初,华中理工大学邓聚龙教授提出灰色系统理论[5-6],该理论把随机过程看作灰色过程,认为任何随机过程都是在一定时间区域和幅值区域变化的灰色量,通过对原始数据的整理找到数据变化规律的过程。虽然采集到的数据没有表现出明显的规律性,而且数据样本较少,但这些数据蕴含着内在规律,利用该理论即可预测出某个时期内的规律,进而用来解决大量实际问题。差分、均值、离散1阶1变量灰色模型(GM(1,1))是灰色系统理论的 3种基本模型。
1.1 差分GM(1,1)模型
假设通过实际测试采集到的原始数据序列为:

其中,k=1,…,n,下同。
对其做一次累加生成[5-6](1-AGO,Accumulating Generation Operation)得到:

式(3)为差分 GM(1,1)模型。α为发展系数,代表的是行为序列估计值的发展态势;b为灰色作用量,是从行为序列中挖掘出来的数据,反映的是数据变化的关系。

其中B,Y分别为:

灰色模型的还原值为:

当k≤n时,x^(0)(k)是原始数据序列 x(0)(k)的拟合值;当 k>n时,x^(0)(k)为原始数据序列的预测值。
1.2 均值GM(1,1)模型
式(9)为均值GM(1,1)模型的白化微分方程,也叫影子方程。

取 x(1)(1)=x(0)(1),则灰色模型方程的解为:
灰色模型的还原值为:
1.3 离散GM(1,1)模型
称:

式(12)为离散GM(1,1)模型。

2 焊点健康预测
焊点连接失效是在外界环境中各种应力的共同作用下,使得焊点逐渐老化、磨损,从而导致其性能下降,焊点的阻抗间歇性升高,随着应力的持续累积,单位时间内,其焊点阻抗间歇性升高的次数越来越多,直到最后完全失效。其变化过程是渐进性的而非突发性的,具有一定的规律性,因此可以运用灰色系统理论实现对焊点未来健康状态的预测,为焊点连接失效的健康管理提供依据。
2.1 数据采集
利用已有监测手段,可以很容易得到两次焊点阻抗间歇性升高之间的间隔时间,以及每次焊点阻抗间歇性升高的持续时间,分别用 Δt1和 Δt2来表示。因为它们是环境应力累积下焊点连接老化的两种表现形式,所以 Δt1和 Δt2之间存在相关性,即 Δt1和 Δt2之间可以相互表示。对Δt1和Δt2的数据规律进行分析可知,在焊点健康状态退化的过程中Δt1从大变小,而Δt2则由小变大。对焊点健康状态的预测主要是在焊点连接退化的早期进行的,这时如果选择 Δt2,由于时间测量的不准确会导致预测精度的降低,故在用灰色模型对焊点连接失效进行预测时使用的数据源为 Δt1。
文中采用的原始数据是故障诊断[7]得到的实测数据Δt1(t/min),分别为:113.4、86.2、83.9、90.5、60.7、65.1、58.8、67.3、25.4、51.4、68、27.8、44.55、17.87、29.2、42.75、26.49、11.37、30.54、20.72、8.1、20.59。取前 6次的数据用来建模及预测,其他实测数据用来与预测值进行对比分析。
2.2 模型建立
由实测数据可得:

建立的3种模型如下:
(1)差分模型

(2)均值模型
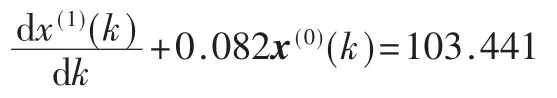
(3)离散模型
2.3 软件仿真
利用MATLAB软件和上面建立的模型,即可预测出两次焊点阻抗间隙性升高的累积时间,与实测值对比如下。
(1)利用差分模型得到的预测值与实测值的对比情况如图1所示。

图1 实测值与预测值对比曲线(差分模型)
(2)利用均值模型得到的预测值与实测值的对比情况如图2所示。

图2 实测值与预测值对比曲线(均值模型)
(3)利用离散模型得到的预测值与实测值的对比情况如图3所示。
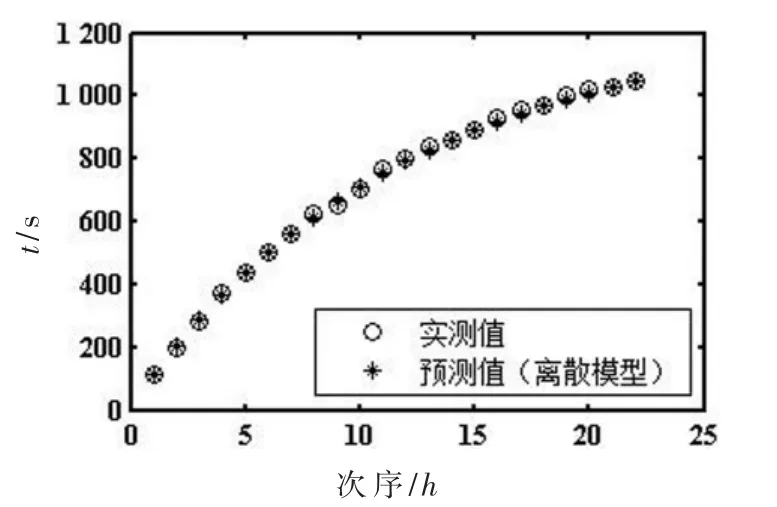
图3 实测值与预测值对比曲线(离散模型)
2.4 结果分析
从仿真结果可以看出,利用灰色系统理论,针对BGA焊点,分别建立的差分、均值、离散GM(1,1)模型,都可以实现对其健康的预测,预测值与实测值基本吻合。通过对比3个图也可以看出,差分模型的预测值略大于实测值,离散模型的预测值略小于实测值,而均值模型的预测值与实测值吻合得较好。
3 结论
(1)把灰色系统理论引入 BGA焊点的健康预测,克服了概率统计、模糊数学难以解决的“小样本”、“贫信息”等困难。
(2)利用灰色系统理论,分别建立了差分、均值、离散三种BGA焊点失效模型。
(3)对比仿真结果,发现均值 GM(1,1)模型的预测值与实测值吻合得更好。
[1]LIU C,WANG J Y,ZHANG A T.Research on the fault diagnosis technology of intermittent connection failure belonging to FPGA solder-joints in BGA package[J].Optik-International Journal for Light and Electron Optics,2013,125(2):737-740.
[2]陈颖,康锐.球栅阵列封装焊点寿命预测的综合方法[J].焊接学报,2009,30(11):105-108.
[3]田园,孙靖国,李大鹏.基于FPGA的 BGA焊点健康管理原理与实现[J].计算机测量与控制,2015,23(10):3310-3312.
[4]PERKINS A,SITARAMAN S K.Universal fatigue life prediction equation for ceramic ball grid array(CBGA)packages[J].Microelectronics Reliability,2007,47(12):2260-2274.
[5]邓聚龙.灰理论基础[M].武汉:华中理工大学出版社,2002.
[6]刘思峰,杨英杰,吴利丰.灰色系统理论及其应用[M].北京:科学出版社,2014.
[7]王建业,丁浩,刘苍.FPGA焊点连接失效故障诊断[J].焊接学报,2014,35(8):66-70.
Prediction on welding point health based on three kinds of GM(1,1)
Zhang Guoli,Wang Heming,Pan Kezhan
(Missile Institute,Air Force Engineering University,Xi′an 710051,China)
In this paper,the grey system theory is used to solve problems during the process of establishing welding point failure model,such as lack of data points,no obvious regularity,difficult to predict,etc.Three kinds of grey model of welding point failure are established,and a prediction about the later status of welding point health is made.The experiment results show that three kinds of grey models can predict welding point health.Predicted and the measured values are consistent.The prediction of even grey model is better than the other two models.
grey model;ball grid array;predict of health
TG405
A
10.16157/j.issn.0258-7998.2016.12.007
张国礼,王和明,潘克战.基于三种 GM(1,1)的BGA焊点健康预测[J].电子技术应用,2016,42(12):31-33.
英文引用格式:Zhang Guoli,Wang Heming,Pan Kezhan.Prediction on welding point health based on three kinds of GM(1,1)[J].Application of Electronic Technique,2016,42(12):31-33.
2016-08-01)
张国礼(1979-),男,硕士,讲师,主要研究方向:微电子学与固体电子学。
王和明(1965-),男,硕士,教授,主要研究方向:微电子学与固体电子学。
潘克战(1972-),男,硕士,高级实验师,主要研究方向:微电子学与固体电子学。
