基于分数阶偏微分的路面裂缝图像增强新模型
2016-12-22洪晓江
洪晓江
(西昌学院 工程技术学院,四川 西昌 615000)
基于分数阶偏微分的路面裂缝图像增强新模型
洪晓江
(西昌学院 工程技术学院,四川 西昌 615000)
为解决传统的整数阶图像增强方法在路面裂缝图像处理效果中的不足,研究了一种新的基于分数阶偏微分的路面裂缝图像增强新模型。首先,针对现有的路面裂缝图像增强方法存在的问题进行分析,提出了采用分数阶微分理论解决路面裂缝边缘信息难以较好保留的问题;其次,根据分数阶微分差分表达式,以Prewitt算子的水平和竖直方向3×3模板为基础,推导出了一种新的5×5梯度掩模;最后,用该模型和传统算子分别对路面裂缝图像进行增强处理。试验结果表明该模型不仅具有大幅提升信号高频成分,增强信号中频成分、非线性保留信号的低频等特性,而且在边缘处达到极值检测边缘,去掉部分伪边缘,对噪声具有平滑作用。
道路工程;路面裂缝检测;分数阶偏微分;图像增强;Prewitt算子
0 引言
数字图像处理技术在路面裂缝检测中的应用[1-4],提高了基于摄像机的路面裂缝识别系统的自动化水平。但背景光照不均匀、存在油污杂物引起的模糊以及在图像传输过程中的噪声污染等原因,使得图像的颜色和细节丢失、视觉效果差。为了更好地分析路面裂缝的程度和细节,需要对识别的图像进行增强预处理。许多学者已将基于三维地形模型的自动检测算法[5]、人工种群算法[6]、神经网络算法[7]等算法和常规图像处理算法相融合使得路面裂缝检测的精度得到提高,但很难克服噪声以及背景光照不均匀的影响。这些检测算法对微观裂缝和网状裂缝处理效果欠佳。更重要的是,程序因运算量过大耗时较长,很难适用于实时检测。在数字图像处理技术中,由一维小波变换利用张量积扩展得到的二维小波变换,在处理边缘纹理细节时并不理想;Contourlet变换由于存在下采样过程,导致缺乏了平移不变性,路面图像增强结果会产生伪Gibbs失真,造成裂缝边缘模糊。
近年来,分数阶微分理论已经成功地应用于各个领域,在图像处理方面也取得许多成果[8-9]。许多研究已经表明,分数阶微分在图像增强中的优越性。将分数阶微分理论与数字图像处理方法相结合用于对图像进行预处理,分数阶微分对图像纹理细节信息的增强效果较好,同时裂缝边缘信息得到保留。
在图像处理算法中,Prewitt算子常用于处理数字图像的边缘轮廓信息,可以在边缘处达到极值检测和平滑噪声,从而能够更精确地识别边缘。本文以分数阶微分为基础,与现有的Prewitt 算子相结合,尝试提出路面裂缝图像增强的新模型。该模型结合了分数阶微分和Prewitt算子两者的优点,在增强图像细节的同时还具有一定的抗噪性。试验结果表明,本文新模型能使路面裂缝图像信噪比得到提高,裂缝细节部分得以保留,且和背景图像比较辨识度较高,从而为提高路面裂缝尺寸计算精度,是一种有效的路面裂缝图像增强新方法。
1 分数阶偏微分的差分表达式
根据分数阶微分的Grumwald-Letnikov(G-L)定义[10-11],导出一元信号f(t)的差分近似表达式为:
(1)
二维数字图像在x和y轴方向上的持续时间以像素为单位进行度量。对于数字图像f(x,y)的差分表达式为:
(2)
(3)
2 基于分数阶偏微分的路面裂缝图像增强新模型
设一副图像的灰度函数为F(x,y),取其3×3像素邻域,如式(4)所示:
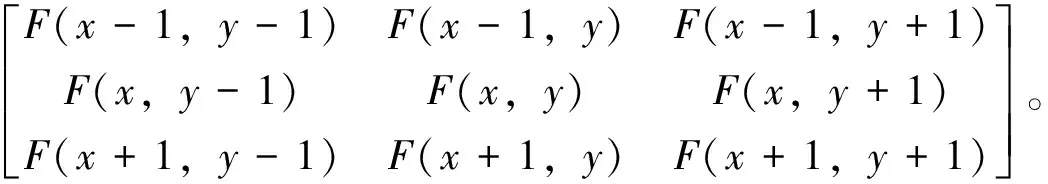
(4)
为了简化运算,在图像处理中常用差分近似代替微分。对于离散灰度函数的3×3区域,Prewitt算子沿不同的方向分为水平梯度和竖直梯度,其具体的表达式分别为式(5)、(6),算子模板见式(7)、(8)。
(5)
(6)
(7)
(8)
(9)
(10)
(11)
将式(10),式(11)的整数阶偏微分用分数阶偏微分来代替,得到新模型如下:
(12)
(13)
为得到准确的图像增强处理效果,采用差分表达式(2)和式(3)的前3项,以便形成3×3微分掩模。另外,结合式(12),式(13)得到Prewitt算子分数阶在水平方向和竖直方向梯度的后向差分形式如下:


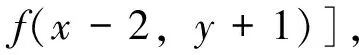
(14)
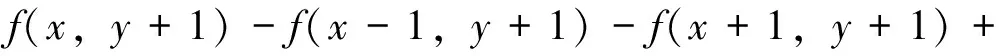
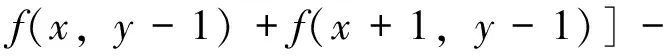

(15)
水平方向的掩模为:
竖直方向的掩模为:
借鉴文献[12]中的方法,将掩模以点(x,y)为中心进行上下左右4个方向旋转,再将其叠加,得到新模型的梯度掩模如下:
3 试验及结果分析
将本文的新模型用Matlab软件进行计算机仿真试验,并与现有的部分图像增强方法进行比较。本文共进行了两组对比试验。

图1 不同阶数图像处理结果Fig.1 Result of various orders image processing
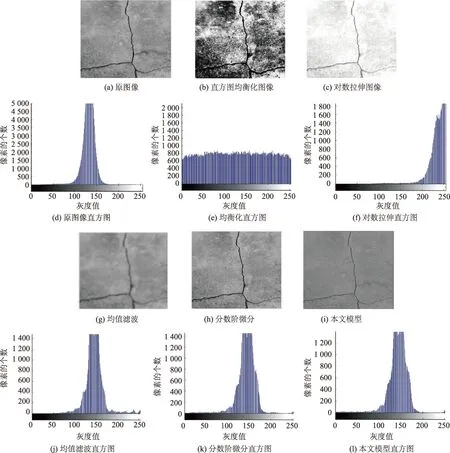
图2 不同增强方法的处理结果Fig.2 Processing result by different enhancement methods
第1组试验是对lf1图像进行增强,试验结果如图1所示。其中,图1(a)为原图像,图1(b)~(f)是新模型取不同的阶数值v得到的路面图像增强结果。由试验结果可知,当0
为了说明本文模型在纹理细节丰富的裂缝图像处理效果的优越性,该模方法能更好地对纹理细节信息进行增强,下面用纹理细节多的图像lf2进行了第2组试验。试验结果如图2所示。
从人眼主观来看,直方图均衡化增强过度,使得增强后的图像与原图背景部分失真过大;对数拉伸后,整体灰度值变大,效果反而不好;均值滤波后,图像整体变得模糊了些;分数阶微分处理后,对纹理细节的增强有一定的效果;本文新模型处理后,不仅在纹理细节方面得到了增强,而且边缘区域较分数阶的增强效果要好些。通过直方图客观来看,原图像的灰度值集中在50~170之间,裂缝处较暗,因此灰度值较小的地方可以看作是裂缝。经过直方图均衡化处理后,灰度值分布较为均匀,但灰度级丢失较多;对数拉伸后,灰度值整体右移,图像整体偏亮;均值滤波后,灰度值范围基本没什么变化,只是将灰度值很大的地方滤除了;分数阶微分增强后,裂缝纹理细节得到了一定的增强,但整体的灰度值与原图像相比偏小了;本文模型处理后,灰度值集中100~170之间,而0~100之间的灰度值增加了,且分布均匀。由此可见,相对于其他方法而言,本文新方法在增强裂缝纹理细节的同时对边缘的增强也较好且失真度较小。
4 结论
本文建立了一种基于分数阶偏微分的路面裂缝图像增强新模型,其中采用的偏微分方法能良好兼顾噪声消除和纹理细节保护;而Prewitt算子在边缘处能达到极值检测边缘的裂缝的作用,对噪声具有平滑的作用。新模型结合了两者的优点,在增强路面裂缝纹理特征的同时,具有一定的抗噪性,而试验结果也验证了这一点。通过与现有方法的对比试验,用直方图作为客观评价,可以很好地看出新模型对路面裂缝图像的增强有很好的效果。另外,没有对如何自适应搜寻最优的分数阶微分阶数以及定量判定路面裂缝增强的最优处理效果做讨论,这些问题将在后续研究中陆续得到解决。
[1] 孙波成, 邱延峻. 路面裂缝图像处理算法研究[J]. 公路交通科技, 2008, 25(2): 64-68. SUN Bo-cheng, QIU Yan-jun. Pavement Crack Diseases Recognition Based on Image Processing Algorithm[J]. Journal of Highway and Transportation Research and Development, 2008, 25(2): 64-68.
[2] 彭博, 蒋阳升, 韩世凡, 等. 路面裂缝图像自动识别算法综述[J]. 公路交通科技, 2014, 31(7): 19-25. PENG Bo, JIANG Yang-sheng, HAN Shi-fan, et al. A Review of Automatic Pavement Crack Image Recognition Algorithms[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 19-25.
[3] 李清泉, 胡庆武. 基于图像自动匀光的路面裂缝图像分析方法[J]. 公路交通科技, 2010, 27(4): 1-5,27. LI Qing-quan, HU Qing-wu. A Pavement Crack Image Analysis Approach Based on Automatic Image Dodging[J]. Journal of Highway and Transportation Research and Development, 2010, 27(4):1-5,27.
[4] 张娟, 沙爱民, 孙朝云, 等. 路面裂缝自动识别的图像增强技术[J]. 中外公路, 2009, 29(4): 301-305. ZHANG Juang, SHA Ai-min, SUN Chao-yun, et al. Image Enhancement Technique for Automatic Identification of Pavement Crack[J]. Journal of China & Foreign Highway, 2009, 29(4): 301-305.
[5] 唐磊, 赵春霞, 王鸿南, 等. 基于图像三维地形模型的路面裂缝自动检测[J]. 计算机工程, 2008, 34(5): 20-21,38. TANG Lei, ZHAO Chun-xia, WANG Hong-nan, et al. Automated Pavement Crack Detection Based on Image 3D Terrain Model[J]. Computer Engineering, 2008, 34(5): 20-21,38.
[6] 张洪光, 王祁, 魏玮. 基于人工种群的路面裂纹检测[J]. 南京理工大学学报:自然科学版, 2005, 29(4): 389-393. ZHANG Hong-guang, WANG Qi, WEI wei. Pavement Distress Detection Based on Artificial Population[J]. Journal of Nanjing University of Science and Technology:Natural and Science Edition, 2005, 29(4): 389-393.
[7] BRAY J, VERMA B, LI X, et al. A Neural Network Based Technique for Automatic Classification of Road Cracks[C]// Proceedings of International Joint Conference on Neural Networks. Vancouver:IEEE, 2006:907-912.
[8] 蒋伟. 基于分数阶偏微分方程的图像去噪新模型[J]. 计算机应用,2011, 31(3): 753-756. JIANG wei. New Image Denoising Model Based on Fractional-order Partial Differential Equation[J]. Computer Applications,2011, 31(3): 753-756.
[9] 杨柱中, 周激流, 黄梅, 等. 基于分数阶微分的边缘检测[J]. 四川大学学报:工程科学版, 2008, 40(1): 152-157. YANG Zhu-zhong, ZHOU Ji-liu, HUANG Mei, et al. Edge Detection Based on Fractional Differential[J]. Journal of Sichuan University: Engineering Science Edition, 2008, 40(1): 152-157.
[10]蒲亦菲. 将分数阶微分演算引入数字图像处理[J]. 四川大学学报:工程科学版, 2007, 39(3): 124-132. PU Yi-fei. Application of Fractional Differential Approach to Digital Image Processing[J]. Journal of Sichuan University:Engineering Science Edition, 2007, 39(3): 124-132.
[11]PINCHERLE I. Fractional Differential Equations[M]. SanDiego: Academic Press, 1990: 20-23.
[12]杨柱中. 分数阶微分在现代信号分析与处理中应用的研究[D]. 成都:四川大学, 2006. YANG Zhu-zhong. Research on Application of Fractional Order Differential in Latest Signal Analysis and Processing[D]. Chengdu:Sichuan University, 2006.
Based on Fractional Differential Enhancement New Model of Pavement Crack
HONG Xiao-jiang
(School of Engineering Science, Xichang College, Xichang Sichuan 615000, China)
In order to solve the problem of the shortcoming of traditional integer order image enhancement method in pavement crack image processing, a new image enhancement model based on fractional order partial differential method is studied. First, in view of the problem in the existing pavement crack image enhancement method, the fractional order differential theory is proposed to solve the problem that the edge information of pavement crack is difficult to be retained. Second, according to the fractional order differential difference expression, a new 5×5 gradient mask is derived based on the 3×3 template at horizontal and vertical directions of the Prewitt operator. Finally, the pavement crack image is enhanced by the new model and traditional operator. The experimental result indicates that this model not only can sizable improve the high frequency components, enhance the intermediate frequency components, nonlinear keep very low frequency characteristics of signal, but also can remove part of the pseudo edge at extreme test edge, which has smoothing effect on noise.
road engineering; pavement crack detection; fractional order partial differential; image enhancement; Prewitt operator
2016-07-26
四川省教育厅科研项目(16ZB0264)
洪晓江(1986-),男,四川西昌人,硕士研究生.(270721068@qq.com)
10.3969/j.issn.1002-0268.2016.12.013
U416.21
A
1002-0268(2016)12-0083-05
