防爆墙设置对单层球面网壳结构抗爆性能的影响
2016-12-22翟希梅苏倩倩
翟希梅,苏倩倩
(哈尔滨工业大学 土木工程学院,哈尔滨150090)
防爆墙设置对单层球面网壳结构抗爆性能的影响
翟希梅,苏倩倩
(哈尔滨工业大学 土木工程学院,哈尔滨150090)
为获得防爆墙设置下大跨网壳结构的抗爆性能,采用ANSYS/LS-DYNA分析软件,首先对设置防爆墙时爆炸冲击波的传播规律进行了有限元模拟和试验结果验证,从而确定流固耦合算法数值模拟的适用性;建立了包含网壳杆件、檩托、檩条、铆钉和屋面板的40 m跨度K8型单层球面网壳在外部爆炸荷载作用下的精细化有限元模型,提取结构在设置防爆墙时的动力响应结果,考察了防爆墙高度、位置和网壳矢跨比对结构动力响应的影响程度,总结了防爆墙及结构参数对冲击波绕流效应及冲击波在防爆墙与建筑物间反射效应的影响规律,提出存在“防爆墙危险高度”情况并给出具体数值,为指导大跨网壳结构合理的抗爆防御设计提供参考依据.关键词: 防爆墙;流固耦合;单层球面网壳;外部爆炸荷载;动力响应
防爆墙作为一种简单、有效的防爆措施,可以减少恐怖爆炸对建筑物结构破坏效应[1].空气冲击波遇到防爆墙的传播规律已有众多学者研究[2-3].Langdon等[4]通过对不锈钢板施加压力脉冲荷载来模拟爆炸,研究了钢板的响应以及连接细节对其性能的影响;Zhou等[5]基于数值模拟提出了刚性墙后峰值压力的估算公式;吴媛媛等[6]对近地爆炸下刚性墙后的绕流现象进行了数值模拟,研究了超压时程规律及影响因素;穆朝民等[7]采用压力传感器测得了防爆墙前后的压力时程,分析了墙对冲击波的影响规律.上述研究多集中于挡墙对爆炸冲击波绕流的机理及超压研究,很少关注挡墙的材料、尺寸等参数.另外,考虑爆炸冲击波绕流效应以及冲击波在建筑物与防爆墙之间相互反射作用对结构的影响较少,对大跨空间结构的影响研究处于空白.同时,对整体结构的爆炸响应研究相对较少[8],主要集中于压力场分布、结构的响应、损伤、失效机理以及防爆泄爆设计.
本文运用ANSYS/LS-DYNA动力有限元分析软件,首先对文献[7]中的爆炸试验进行有限元验证,以确定多物质的流固耦合方法(arbitrary-lagrange-euler,ALE)的准确性;建立精细化40 m跨度的K8型单层球面网壳模型,提取网壳在设置防爆墙时外部爆炸荷载作用下的动力响应,得出了不同防爆墙参数设置对结构动力响应的影响规律,分析了冲击波绕流效应及冲击波在防爆墙与建筑物间的反射效应对结构的影响,为进一步指导大跨网壳结构的防爆墙设计提供依据.
1 试验验证
1.1 试验简介及有限元模型
为验证ALE数值模拟方法在分析防爆墙对爆炸冲击波影响的正确性,本文对文献[7]的防爆墙爆炸试验进行数值模拟.如图1(a)所示,试验模型由空气、炸药、挡墙组成.4 kgTNT炸药放置在距离墙3 m的防爆墙中轴线上,离地高0.6 m.墙前离地高1.5 m和0.6 m分别设置A、B两个测点;墙后在与爆心同一水平位置,由近及远设置7个测点.

图1 试验布置及有限元模型
用有限元软件LS-DYNA对上述试验进行有限元模拟.模型包括炸药、空气、地面和挡墙,挡墙尺寸为0.5 m×3 m×2.5 m,采用MAT_Concrete_Damage_Rel3材料模型[9],底部为固定约束.炸药位置、药量同试验设置保持一致.考虑到试验模型的对称性,有限元建模时采用1/2模型,对称面处设置对称边界条件.有限元模型如图1(b)所示.空气域为12 m×8 m×8 m(包裹炸药、挡墙及所需测点),空气及炸药的网格划分尺寸皆为0.075 m.空气、炸药和挡墙采用SOLID164单元,算法为多物质ALE算法.地面采用反射边界条件,其他边界设置为无反射边界条件.
TNT炸药为立方体装药,采用MAT-High-Explosive-Burn材料模型,并用Jones-Wilkins-Lee(JWL)状态方程作为炸药爆轰产物的控制方程[9]:
(1)
表1给出了TNT炸药的主要材料参数.空气采用Mat-Null材料模型和Eos_Liner_Polynomial状态方程[9]:
(2)
表2给出了空气材料参数.

表1 炸药材料参数

表2 空气材料参数
1.2 数值模拟结果与误差分析
图2给出了不同时刻冲击波传播状态下的压力分布图,表明了冲击波遇到挡墙时的反射以及绕过挡墙继续传播的全过程.
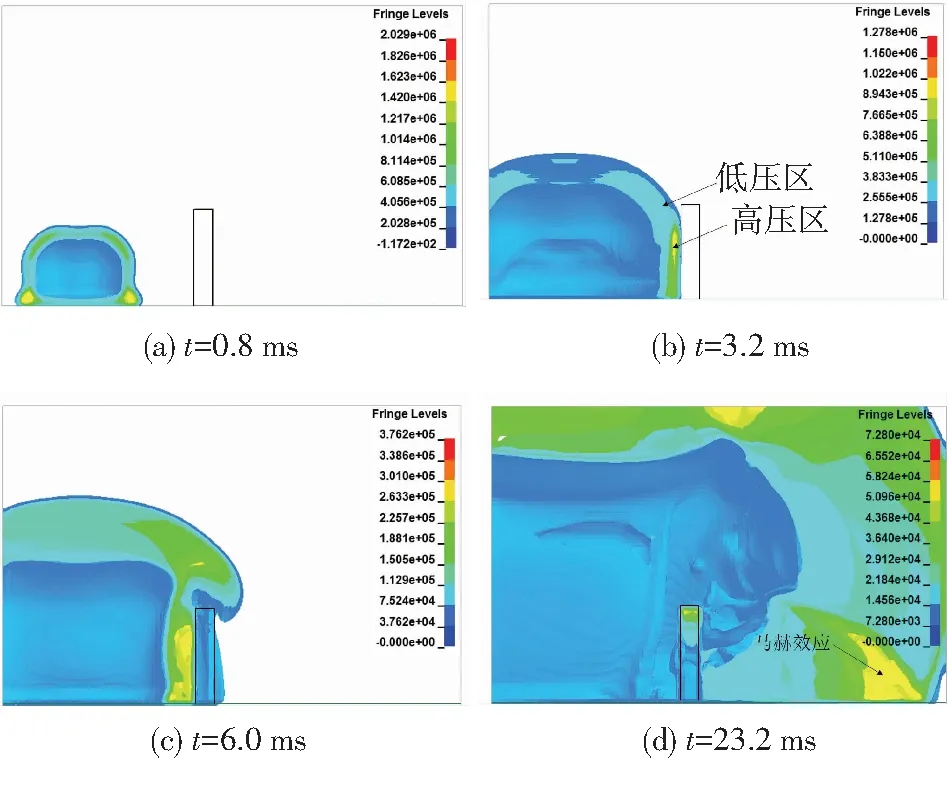
图2 不同时刻冲击波压力分布
从图2可以看到冲击波传播时先遇到地面,发生反射,地面附近压力较大(t=0.8 ms),经地面发射的冲击波和原先向前传播的冲击波一起向前运动,作用于墙正面,反射使壁面压力增高(t=3.2 ms),未遇到挡墙阻碍的冲击波压力较小,形成超压差,引起高压区空气向边缘低压区流动.在稀疏波的作用下,前墙处空气向边缘运动(t=6.0 ms),对挡墙侧面和顶部产生压力,同时在边缘入射波的影响下形成顺时针的旋风,旋风又和相邻的入射波一起作用,形成环流绕过墙顶部沿着墙后壁向下运动,经地面反射,并在墙后一定距离处形成马赫反射 (t=23.2 ms).
数值模拟分析得到测点的反射、绕射超压时程曲线如图3所示,测点位置见图1(a)所示.从图3可以看出数值模拟结果与试验基本吻合, A、B测点在3 ms左右达到超压峰值,墙后1、4测点在20 ms左右达到峰值,之后慢慢衰减.而且墙后测点的峰值超压比墙前小一个数量级.试验与有限元模拟结果对比如表3所示,可以看到,峰值超压最大误差为21.94%.上述对比结果说明本文采用ALE方法来模拟挡墙对爆炸冲击波的影响分析是可行的.
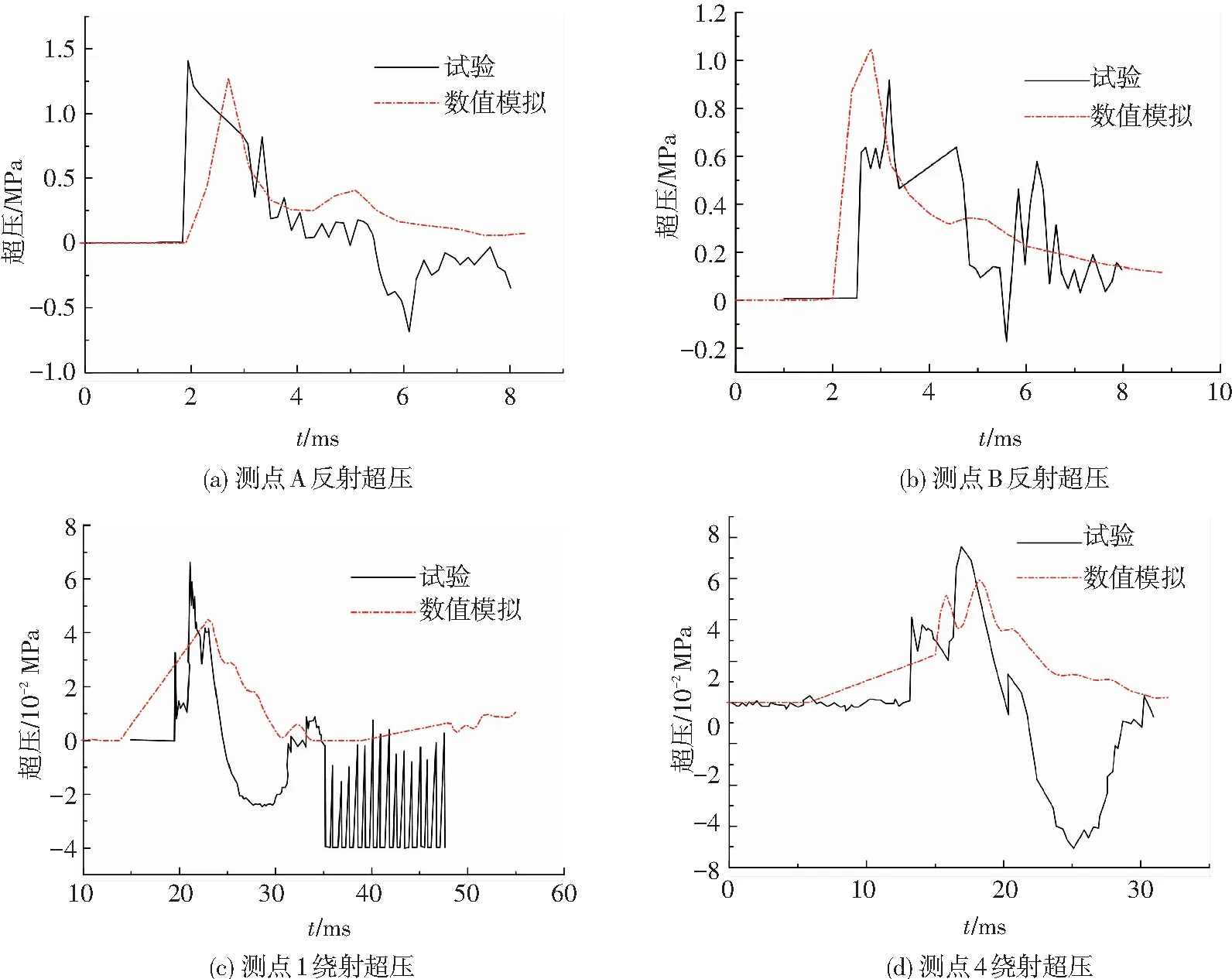
图3 测点超压时程对比

测点峰值超压试验值PT/MPa峰值超压数值模拟值PS/MPaPS-PTPT/%A1.39501.2775-8.42B0.92791.052213.3910.05300.0453-14.5340.07610.0594-21.94
2 防爆墙对单层球面网壳的影响
2.1 有限元模型介绍
建立了40 m跨度、矢跨比1/5~1/7、分频数为6的精细化K8型单层球面网壳模型:自上而下依次为屋面板、铆钉、檩条、檩托、网壳杆件.同时,在距离网壳最外边缘一定距离处建立刚性防爆墙模型[10].选用多段线性塑性模型模拟钢材,并采用Cowper-Symonds模型考虑应变率,以有效地反映应变率对钢材强度的影响.钢材的初始屈服应力为207 MPa;弹性模量为206 GPa;泊松比为0.3;失效时的有效塑性应变为0.25.
K8型单层球面网壳模型见图4.网壳杆件的截面尺寸见表4,檩托采用圆钢管Φ76×4.0 mm,檩条采用箱型截面140 mm×50 mm×1.75 mm×3.5 mm,铆钉直径为12 mm,屋面板采用1 mm厚的钢板.檩托和檩条以及屋面板和铆钉之间均采用共节点的连接方式,底部采用三向不动铰支座固定网壳.
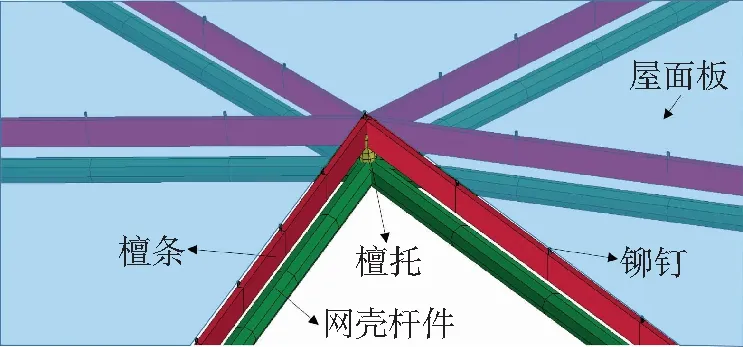
图4 网壳模型示意
建模时由于结构对称性,取1/2结构模型,有限元模型见图5.炸药和空气设置同第一部分.网壳杆件、檩托、檩条、铆钉用BEAM161单元,屋面板和防爆墙用SHELL163单元来模拟,采用多物质ALE算法,对称面处采用对称边界条件,地面采用反射边界条件,其他边界采用透射边界条件.
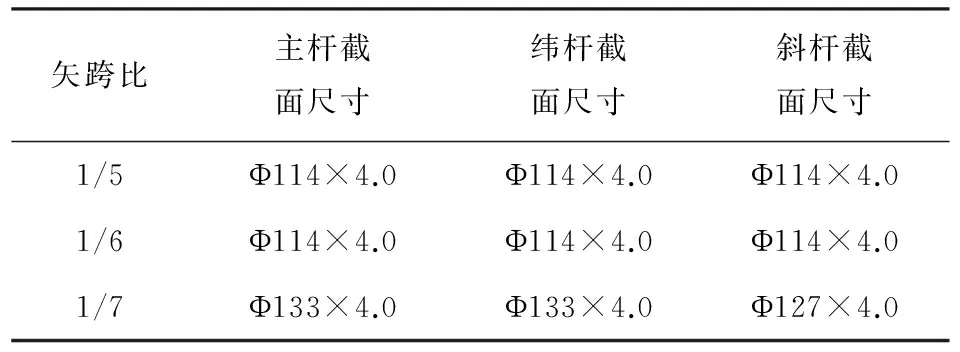
表4 主杆、纬杆和斜杆的截面尺寸
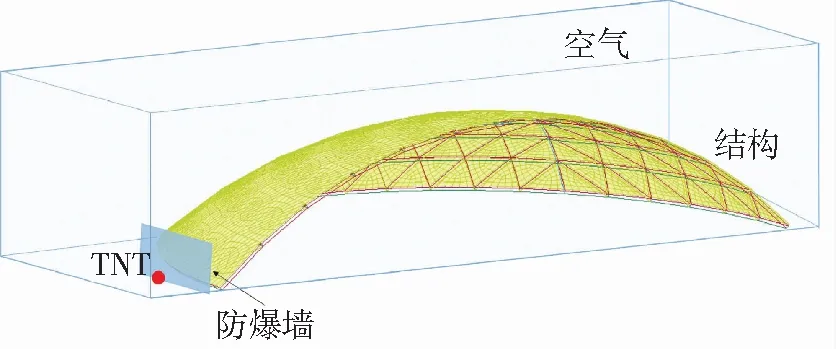
图5 有限元模型
保持TNT炸药距离网壳最外边缘6 m、距网壳底部水平面0.9 m不变,在炸药与K8型球面网壳之间设置一道防爆墙,防爆墙至网壳最外边缘的距离为D,防爆墙的高度为H,长度为L.为了便于说明,每个算例以不同编号表示,定义如下:D为防爆墙距离网壳最外边缘距离,L为防爆墙长度,F为矢跨比的倒数,H为防爆墙高度,编号为D5L10F5H1的算例即表示防爆墙长10 m,高1 m,距离矢跨比为1/5的网壳最外边缘5 m.本文除了特殊说明下,TNT炸药当量均为104 kg,并设置在结构对称面上.
2.2 防爆墙高度的影响
为研究防爆墙的高度对外部爆炸荷载作用下网壳动力响应的影响, 保持防爆墙长10 m,距离矢跨比为1/5的网壳最外边缘2 m不变, 仅改变防爆墙的高度H, 分别取值为 0.5、0.75、1、1.5和2 m 进行建模(即防爆墙高度与网壳矢高的比值从1/16增大到1/4),分析网壳的动力响应.
本文定义网壳合位移最大的节点为最大位移节点,这个节点的位移称为最大节点位移,最大节点位移能够反应网壳的刚度,本文所分析的D2L10F5系列模型计算得到的网壳的最大节点位移时程曲线和最大位移如图6所示.同时,为了对比有无防爆墙对结构动力响应的影响,建立了无防爆墙的外爆模型(炸药位置和药量保持不变).结构的节点位移和动力响应如图6和表5所示(0表示无防爆墙).
从图6和表5可看出,随着防爆墙高度与网壳矢高的比值从1/16增大到1/4,网壳的最大节点位移、结构(网壳杆件、檩条、檩托、屋面板、铆钉)的平均塑性应变以及网壳杆件的1P、4P百分比均呈现出先增大后减小的变化趋势.并且,结构所有构件均没有出现断裂破坏,只是进入了不同程度的塑性发展.具体说来,当防爆墙高度与网壳矢高的比值为1/16时,网壳最大节点位移比没有防爆墙时小6.49%,说明设置防爆墙对冲击波有一定的阻挡作用.但当防爆墙高度与网壳矢高的比值增大到3/32时,网壳的最大节点位移达到2.1881 m,比没有防爆墙时大9.67%,此时,各构件平均塑性应变和网壳杆件的1P、4P百分比也达到最大.当防爆墙高度与网壳矢高的比值增大到1/8以上时,网壳最大节点位移比没有防爆墙时小了50%以上,说明防爆墙的阻挡作用明显,结构处于安全的状态.
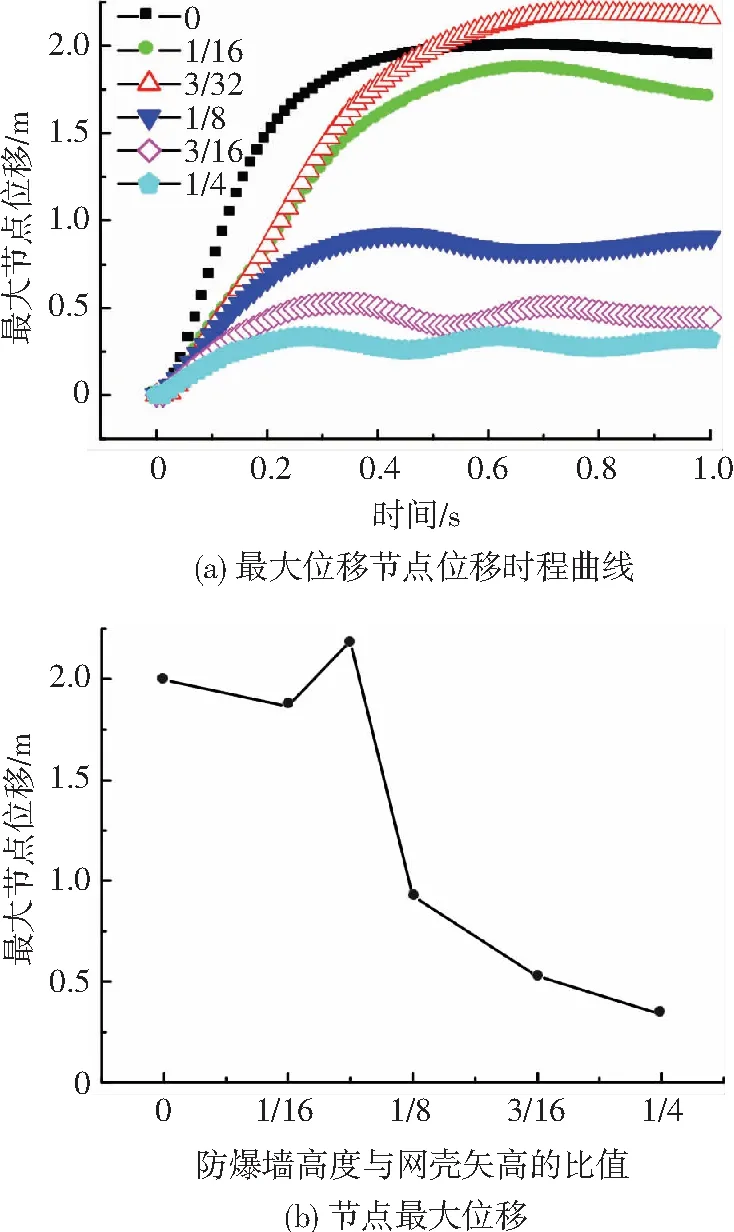
图6 防爆墙高度不同时的节点位移
Fig.6 Nodal displacement in various heights of the explosion-proof wall
防爆墙高度不同时,爆炸冲击波传播过程中压力分布见图7.当防爆墙高度与网壳矢高的比值超过某一限制(3/32)时,防爆墙对爆炸冲击波的绕流作用明显,从顶部和侧面绕到防爆墙后的爆炸冲击波与之前直接向前传播的爆炸冲击波在墙后相互碰撞而叠加增强(图7(b)),进而作用于结构上,使得结构的响应增大,并且比没有防爆墙时的响应还大.当防爆墙高度继续增加时,由于入射角(正切值为炸药中心到墙顶部的垂直距离比炸药中心距墙防爆墙的水平距离)增大,防爆墙的阻挡作用增强,绕流不明显,大部分爆炸冲击波都被防爆墙反射回去,较少的爆炸冲击波发生绕流并继续向前传播(图7(c)),所以网壳的响应较小.

表5 防爆墙高度不同时的结构动力响应统计
注:di表示防爆墙高度为i时结构的最大节点位移.平均塑性应变指各不同构件所有单元的塑性应变平均值.本文使用BEAM161单元来模拟网壳的杆件,该单元的截面共有4个积分点.按照截面屈服程度的不同分别定义了1P、2P、3P、4P四种情况,1P表示截面上至少一个积分点发生塑性屈服,4P表示全截面都进入塑性屈服状态.不同屈服程度杆件比例可以从微观角度反映结构塑性发展的广度和深度.

图7 防爆墙高度不同时的爆炸冲击波传播过程中压力分布
2.3 防爆墙位置的影响
为研究防爆墙的位置对爆炸荷载作用下网壳动力响应的影响, 在数值分析模型中, 选取矢跨比为1/5的网壳,保持防爆墙长10 m不变,改变防爆墙至网壳最外边缘的距离D,分别取值为1、2、5 m,建模分析网壳在防爆墙阻挡作用下的动力响应.D1L10F5、D2L10F5以及D5L10F5系列模型计算得到的网壳动力响应分别如图8和表6所示.
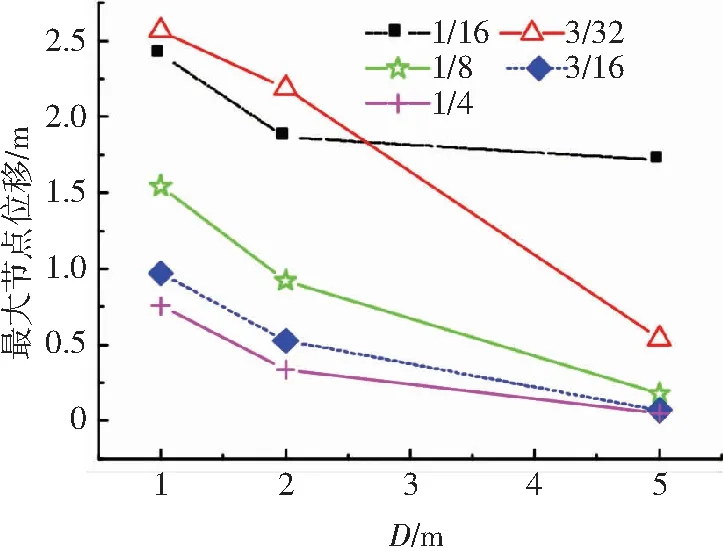
图8 防爆墙位置不同时的节点位移
Fig.8 Nodal displacement in various positions of the explosion-proof wall
从图8和表6可以看出,相同防爆墙高度时,随防爆墙距离网壳最外边缘距离的增大(D越大),网壳的最大节点位移、结构(网壳杆件、檩条、檩托、屋面板、铆钉)的平均塑性应变以及网壳杆件的1P、4P百分比均呈现减小的趋势.另外,同一防爆墙高度下,D1系列模型的位移响应较D5系列模型大,且随防爆墙高度的增加,相应提高程度十分显著,如随着防爆墙高度与网壳矢高的比值从1/16增大到1/4,D1系列模型的位移响应比D5系列模型的位移响应增大的百分比从29.25%提高到93.09%.
防爆墙位置不同时,爆炸冲击波传播过程中压力分布如图9所示.结构的动力响应出现上述规律,是因为:1)防爆墙高度相同时,防爆墙距离网壳最外边缘距离越小,距离爆炸中心的距离越远,即从近场爆炸到远场爆炸,入射角越小,墙后1.5~2.5倍墙高区域内的绕流叠加增强作用明显[7],所以结构的动力响应变大(见图9(a)),反之,防爆墙距离网壳最外边缘越远,距离爆炸中心越近,对爆炸冲击波的阻挡作用越好,爆炸冲击波的反射效应越大,结构的响应越小(见图9(b));2)防爆墙距离爆炸中心越远,爆炸冲击波越容易从墙的两侧发生绕流,进而和从墙体上部绕流的波叠加一起作用到结构上,使得结构的响应变大(见图9(a));3)防爆墙距离网壳越近,绕过防爆墙作用到结构上的爆炸冲击波可以反射到防爆墙背后,进而被防爆墙反射再次作用到结构上,使得结构的响应变大(见图9(a)).
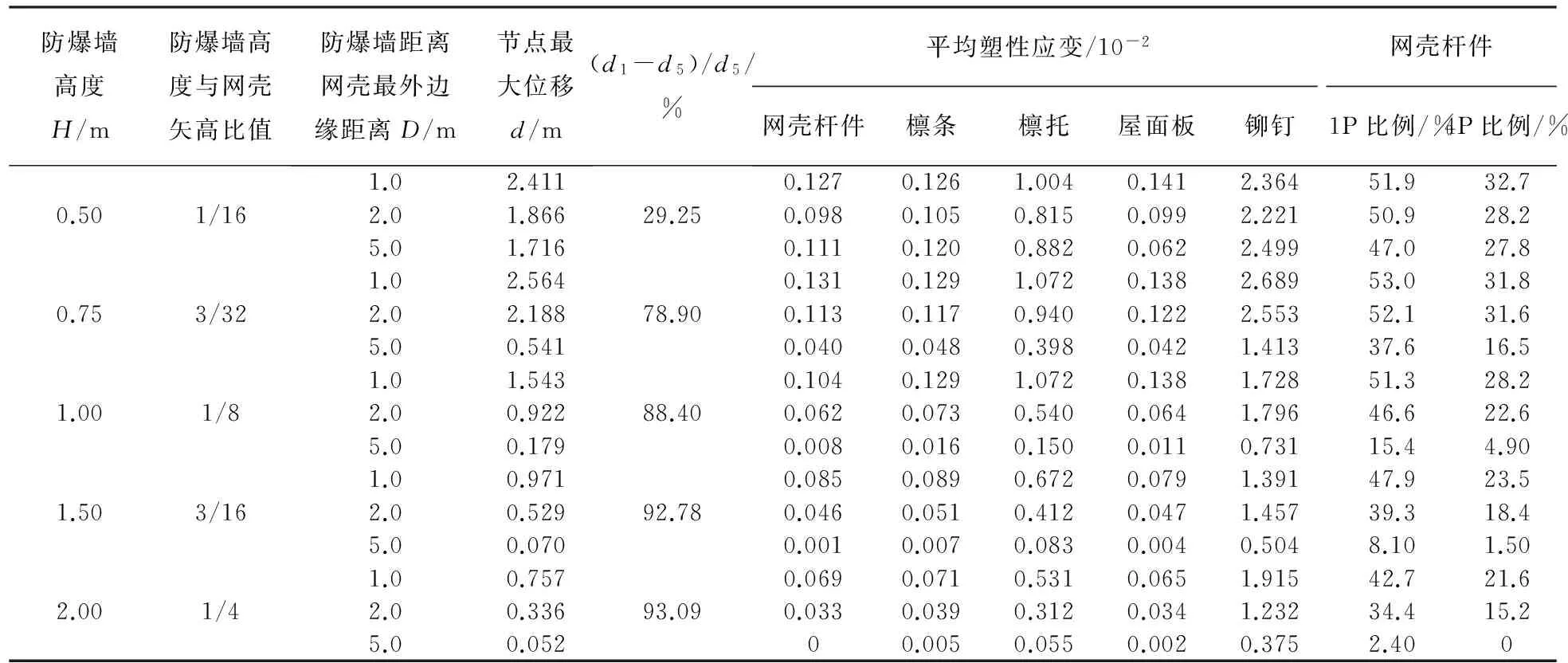
表6 防爆墙位置不同时的结构动力响应统计
注:d1、d2、d5分别表示防爆墙距离网壳最外边缘距离为1、2、5 m时结构的最大节点位移.
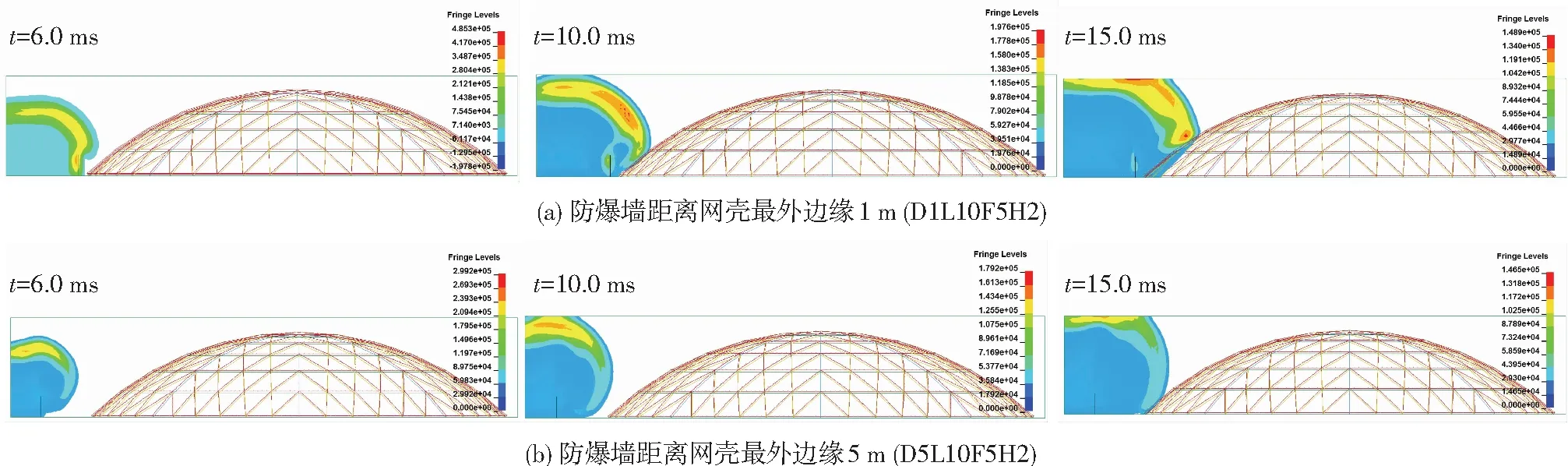
图9 防爆墙位置不同时的爆炸冲击波传播过程中压力分布
2.4 网壳矢跨比的影响
保持防爆墙长度10 m和距离网壳最外边缘1 m不变,选取矢跨比为1/5、1/6和1/7,分析网壳的动力响应.D1L10F5、D1L10F6以及D1L10F7系列模型计算得到的网壳的节点位移和动力响应分别见图10和表7.从图10和表7可看出,防爆墙高度相同时,网壳矢跨比越大,结构各动力响应均呈现增大的趋势.当防爆墙高度与网壳矢高的比值为1/16~1/8时,矢跨比对结构响应的影响较大,而比值为3/16和1/4时,矢跨比对结构的影响较小,即防爆墙越高,结构对矢跨比变化越不敏感.当防爆墙高度与网壳矢高的比值为1/16~1/4时,要想达到相同的防爆效果,网壳矢跨比越大,防爆墙要设置的越高.

图10 网壳矢跨比不同时的节点位移
Fig.10 Nodal displacement in various rise-span ratios of reticulated shell
针对上述结果,本文认为,当防爆墙高度、长度及位置相同时,网壳矢跨比越大,网壳越高,爆炸冲击波的传播方向与与结构夹角越大,迎爆面积越大,作用在结构上的爆炸冲击波能量越多,所以结构的响应增大;同时,网壳矢跨比越大,作用于网壳的水平分力越大,同时,由于网壳水平刚度下降,其抵抗爆炸荷载的能力也减弱;另外,网壳矢跨比越大,网壳越高,爆炸冲击波在防爆墙与网壳屋面板之间的相互反射作用越强,从而使得结构的响应变大.

表7 网壳矢跨比不同时的结构动力响应统计
3 结 论
本文通过有限元软件ANSYS/LS-DYNA采用多物质ALE算法,对外部爆炸荷载作用下40 m跨度、矢跨比为1/5~1/7、分频数为6的K8型单层球面网壳模型进行了防爆墙设置情况下的结构响应分析,考察了防爆墙的高度、位置、长度及网壳矢跨比等参数设置对最大节点位移、构件平均塑性应变、网壳杆件截面屈服程度等动力响应的影响规律,具体结论如下:
1)其他条件不变时,随防爆墙高度的增加,网壳爆炸响应呈现先增大后减小的趋势;当防爆墙高度与网壳矢高的比值为3/32时,此高度处于防爆墙危险高度范围内,因绕流效应叠加的原因,使得网壳结构的爆炸响应比无防爆墙时增大约9.67%,设计时应予以避免.
2)炸点位置不变时,随防爆墙与网壳结构距离的增大,结构的动力响应呈现减小的趋势;并且,最大节点位移响应降低程度随防爆墙高度的增加更为显著,因此,要达到相同的防爆效果,离网壳越近的防爆墙需要建立的越高.
3)当防爆墙高度与网壳矢高的比值为1/16~1/4时,相同墙高下,网壳矢跨比越大,结构的动力响应呈现增大的趋势;要想达到相同的防爆效果,网壳矢跨比越大,防爆墙要设置的越高,尤其是当防爆墙高度与网壳矢高的比值为3/32时.
[1] 伍俊,刘晶波,闫秋实. 装配式防爆墙和翻转式路刺组合防护结构[J]. 土木工程学报, 2008,41(01):99-103. WU Jun, LIU Jingbo, Yan Qiushi. Combined protective structures of fabricated anti-blast wall and turnover road stab[J]. China Civil Engineering Journal, 2008,41(1):99-103.
[2] 郝莉,马天宝,王成,等. 爆炸冲击波绕流的三维数值模拟研究[J]. 力学学报,2010, 42(6): 1042-1049. HAO Li, MA Tianbao, WANG Cheng, et al. Three dimensional numerical simulation study on the flow of the explosion shock wave around the wall[J] . Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1042-1049.
[3] 洪武,范华林,金丰年,等. 刚性防爆墙迎爆面荷载计算方法研究[J]. 工程力学,2012, 29(11): 228-235. HONG Wu, FAN Hualin, JIN Fengnian, et al. Blast response of inclined rigid walls[J]. Engineering Mechanics, 2012, 29(11): 228-235.
[4] LANGDON G S, SCHLEYER G K. Deformation and failure of profiled stainless steel blast wall panels. Part III: finite element simulations and overall summary[J]. International Journal of Impact Engineering, 2006, 32(6): 988-1012.
[5] ZHOU X Q, HAO H. Prediction of airblast loads on structures behind a protective barrier[J]. International Journal of Impact Engineering, 2008, 35(5): 363-375.
[6] 吴媛媛,宋振森. 挡墙后爆炸冲击波绕流现象研究[J]. 河北工程大学学报(自然科学版),2014,31(2):9-14. WU Yuanyuan, SONG Zhensen. Research on diffraction flow effect of explosion shock wave behind blast wall[J]. Journal of Hebei University of Engineering (Natural Science Edition), 2014,31(2):9-14.
[7] 穆朝民,任辉启,李永池,等. 爆炸冲击波作用于墙体及对墙体绕射的实验研究[J]. 实验力学, 2008, 23(2): 169-174. MU Chaoming, REN Qihui, LI Yongchi, et al. Experimental study of blast wave reflection and diffraction on a shelter wall[J]. Journal of Experimental Mechanics, 2008, 23(2): 169-174.
[8] HUSON P, ASARO R J, STEWART L, et al. Non-explosive methods for simulating blast loading of structures with complex geometries[J]. International Journal of Impact Engineering, 2011, 38(7): 546-557.
[9] LS-DYNA. Keyword user’s manual[M]. California: Livermore Software Technology Corporation, 2014.
[10]SHI Y, HAO H, LI Z. Numerical simulation of blast wave interaction with structure columns[J]. Shock Waves, 2007, 17: 113-133.
(编辑 赵丽莹)
Effect of explosion-proof wall on antiknock performance for single-layer reticulated shell
ZHAI Ximei, SU Qianqian
(School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)
To analyze the influence of explosion-proof wall on antiknock performance for large-span reticulated shell structures, propagation of blast shock waves around explosion-proof wall was simulated with finite element software ANSYS/LS-DYNA. The ALE (Arbitrary-Lagrange-Euler) algorithm was determined due to good agreement with experiment. A kiewitt8 single-layer reticulated shell of refinement was established to simulate the dynamic responses of structure considering explosion-proof wall subjected to external blast loading. The response rules of the structure with varied height, position of explosion-proof wall and span ratio of reticulated shell were obtained to analyze the effects of explosion-proof wall and structure on circulating and reflecting action of blast shock wave. Dangerous height of explosion-proof wall including specific values was proposed, which could provide reference for reasonable defense design of reticulated shell structure.
explosion-proof wall; ALE (Arbitrary-Lagrange-Euler); single-layer reticulated shell; external blast loading; dynamic response
10.11918/j.issn.0367-6234.2016.12.010
2015-10-14
国家自然科学基金(51378151)
翟希梅(1971—),女,教授,博士生导师
翟希梅,xmzhai@hit.edu.cn
TU395
A
0367-6234(2016)12-0076-07
