关联色噪声对集合种群稳定性和平均灭绝时间的影响

王 国 威

(1.南昌工学院 基础教学部， 南昌 330108; 2.南昌工学院 非线性力学重点实验室， 南昌 330108)



关联色噪声对集合种群稳定性和平均灭绝时间的影响

王 国 威1，2*

(1.南昌工学院 基础教学部， 南昌 330108; 2.南昌工学院 非线性力学重点实验室， 南昌 330108)

基于Levins模型的研究基础上，大量研究者对“集合种群”稳定性方面的问题进行了探讨，但是之前的大多数研究都局限于确定性Levins模型，或者只是单纯地在系统中加入理想的白噪声.本文根据经典的存在生境破坏的集合种群模型，分析了具有相同关联时间的色关联高斯色噪声对集合种群稳定性的影响，根据统一色噪声近似的方法，推导出集合种群模型的近似福克-普朗克方程(AFPE)，在稳态情况下，得到系统稳态概率分布函数(SPDF)的解析解.应用最速下降法，得到系统的平均灭绝时间(MFPT)的解析表达式.对计算结果进行数值分析，最终的图像分析表明：(1)加性噪声强度D的增加导致Levins模型中集合种群稳定性被弱化，而乘性噪声强度Q的增加对Levins模型中集合种群的稳定性会产生不利影响；(2)τ的增加使集合种群的稳定性得到强化；(3)噪声正关联时(0<λ<1)，|λ|的增大会增加集合种群的稳定性；而负关联时(-1<λ<0)，|λ|的增大却会使集合种群的稳定性弱化；(4)平均灭绝时间T(xs→x0)是Q的减函数，Q的增加会促使集合种群平均灭绝时间减小；(5)T(xs→x0)是τ的单调增函数，τ的增加延缓集合种群的灭绝.

Levins模型； 集合种群； 色噪声； 灭绝； 稳定性

集合种群问题的研究是当今生态学探讨的核心问题之一，生态环境破坏已经成为物种多样性保护和物种续存问题最严峻的挑战，探索外部生存环境的随机动荡对集合种群稳定性的影响已经成为集合种群研究的一个重点内容[1-2].1969年，Levins[3]最早提出了“集合种群”的概念.现在，Levins模型[4]被广泛讨论、研究和应用，并被誉为“集合种群之母”[5-9].然而，之前大部分学者所做的工作都是围绕确定论方程展开的，对于集合种群在随机噪声影响下会呈现出怎样的演化趋势却鲜有研究.基于集合种群模型的基础，王参军等[10]探讨了具有白相关形式白噪声和集合种群系统稳定性之间的关系，利用经典存在生境破坏集合种群的FPE得到系统的SPDF和MFPT；李江城[11]等学者于2008年利用一种简化的延时率函数模型研究集合种群的稳定性，对Levins模型中集合种群的SPDF和MFPT进行解析解计算和数值分析；2013年，王康康等[12]在集合种群模型的基础上，重点论述色交叉关联噪声会如何影响Levins模型中集合种群的稳定性；马祖飞等[13]在2003年研究了集合种群生存过程中的统计随机性与环境随机性，并讨论了这两类随机性对种群灭绝的影响.本文在经典的集合种群模型的基础上，引入更接近实际情况的色噪声来体现集合种群演化过程中的随机不可预知事件，通过计算Levins模型的SPDF和MFPT，研究了色关联色噪声对集合种群系统稳定性的影响.

1集合种群模型的SPDF和MFPT

1.1模型

Levins模型可以表示为

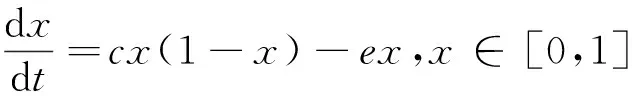
(1)

其中,x代表该系统中已经被占领的生境斑块比值的大小，取值范围是0≤x≤1.e代表系统中局部种群灭绝率的大小，c是一个参数，与扩散个体入侵到新的生境斑块的比例有直接关系.

上面介绍的方程(1)为确定性Levins模型，并没有考虑集合种群生存环境中外部存在的环境扰动因素，也忽略了集合种群内部的先天性基因、后天性个体差异等随机因素.但是，现实生态环境中具体的种群演化过程并不是这样的，因为集合种群在演化过程中会遇到很多不可预知的客观事件(即所谓的噪声).这里，我们认为客观存在的随机环境因素(如某年突然降临意外霜冻或者在多雨寒冷的春季)会影响集合种群的灭绝率e，用更符合实际情况的高斯色噪声ξ(t)代表集合种群生存环境的波动，那么就可以得到e→e+ξ(t).从另外一个因素考虑，斑块生境中存在着一种小种群的集合即异质种群，它们被生存空间天然地隔离，相互之间通过集合种群中某些个体的扩散从而产生某种相互联系，那么在集合种群内部的这种局部种群之间，它们就具有相互影响.当局部种群的数量接近于灭绝的时候，个体的数量很少，具有非常大的随机性，在这里可以认为此随机性为集合种群内部的随机性，基于这种考虑，同样通过引入高斯色噪声η(t)来代表这种情况下的内部随机性.虽然内、外部噪声属于非同源的，不过由于外部环境因素的随机波动会影响内部噪声的涨落，所以内、外部噪声就不再是独立的，也就是说它们之间存在着某种关联，即我们可以引入关联噪声.

把以上因素加以综合考虑，根据方程(1)，通过推理得到集合种群的随机演化方程，即郎之万方程(LE)：

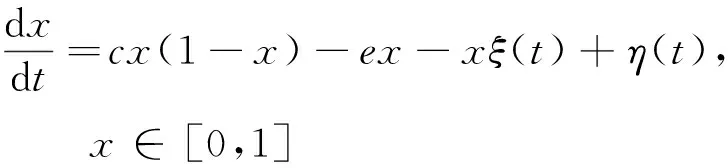
(2)

式中,ξ(t)和η(t)为高斯色噪声，其统计性质为[14]:

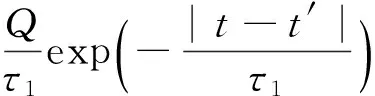
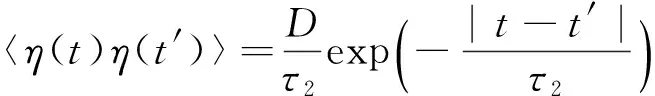
(3)

式中，Q代表加入系统中乘性噪声的强度，D代表加入系统中加性噪声的强度，λ代表乘性噪声和加性噪声之间的色交叉关联强度.当-1<λ<0时，乘性噪声和加性噪声之间的关联为负相关关联形式；当0<λ<1时，意味着两噪声之间为正相关关联形式；τ1、τ2分别代表乘性噪声、加性噪声的自关联时间，τ3是乘性噪声和加性噪声之间的交叉关联时间.t和t'代表两个不同的时间.方程式(2)中关于变量x的确定论势函数为:

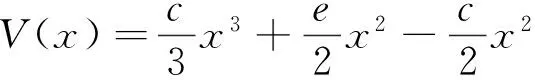
(4)

1.2稳态概率分布函数

应用统一色噪声近似[15]，得到方程(2)～(4)对应的近似Fokker-Planck方程:

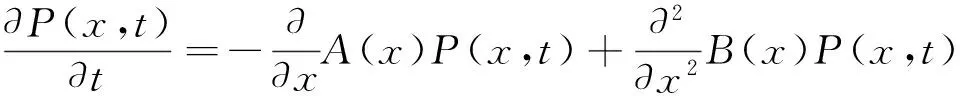
(5)

其中，

(6)

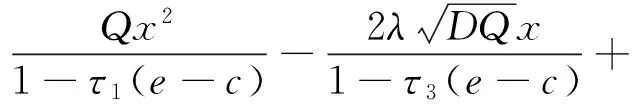
(7)

在定态条件下，求解其稳态概率分布函数为[16]:

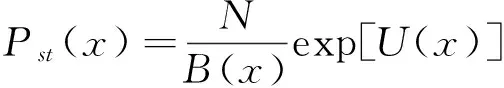
(8)

其中，N为积分常数.在这里，我们取τ1=τ2=τ3=τ，即高斯色噪声具有相等的自关联时间和交叉关联时间，上式中U(x)为系统的修正势函数.根据计算可得U(x)的表达式为

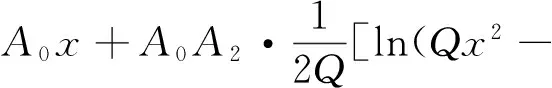
(9)

其中，

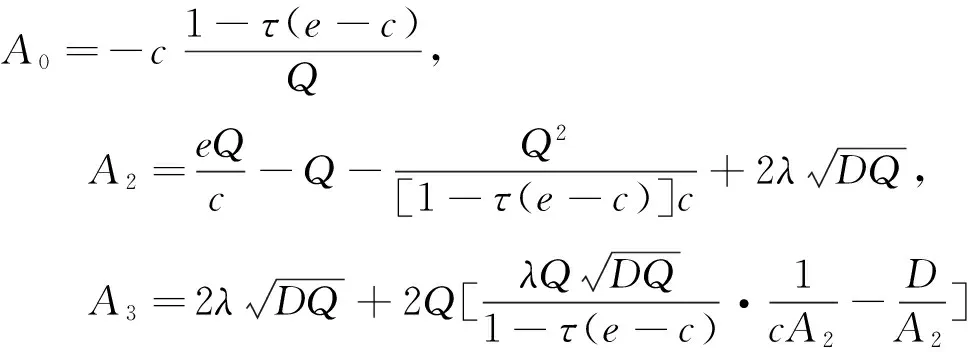
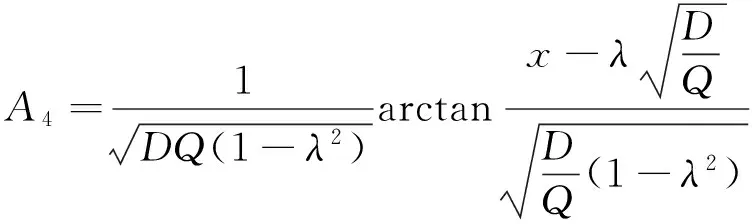
(10)

1.3平均灭绝时间

对于Levins模型而言，集合种群什么时候趋于灭绝是生态学家研究集合种群稳定性问题时重点关注的主要内容，这里根据文献[10]所述用Levins模型系统的MFPT来衡量集合种群的平均灭绝时间，即集合种群从系统的稳定态xs演化到灭绝态x0(即不稳定态)所需要的时间，则可以得到我们所考虑的系统平均灭绝时间的精确解析表达式[10，17]

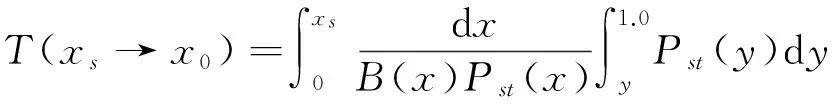
(11)

式中，T(xs→x0)代表集合种群从系统的稳定态xs=1-e/c趋于灭绝态x0=0所需要的平均时间.利用最快下降法[18-21]，得到系统的平均首次通过时间的表达式为[22-23]

T(xs→x0)=

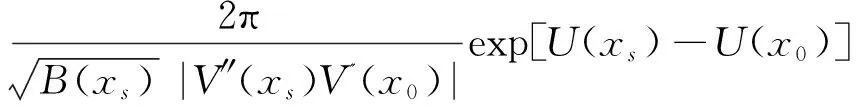
(12)

其中,V(x)和U(x)分别由(4)和(9)式给出.

2噪声对系统稳态性质的影响

根据方程(8)做出稳态概率分布函数Pst(x)作为x的函数，分别以乘性噪声强度D和加性噪声强度Q作为参数的图像[24-27]如图1(a)和(b)所示.

2.1噪声强度对系统稳定性的影响

通过对图1(a)的分析可以发现：当加性噪声强度D逐渐增大时，Pst(x)曲线的峰值会出现逐渐降低的趋势，最后Pst(x)曲线变成一单调曲线.这表明，D的增大会减小被占据的生境斑块的比例在峰值处的概率，即弱化了集合种群的稳定性；而峰值逐渐消失，则表明D的增大使得集合种群逐渐趋向灭绝，即系统从一稳定态向另一个稳定态转变，发生相变[28-29]，故外部环境的波动加剧促使集合种群从稳定态xs转向灭绝态x0.

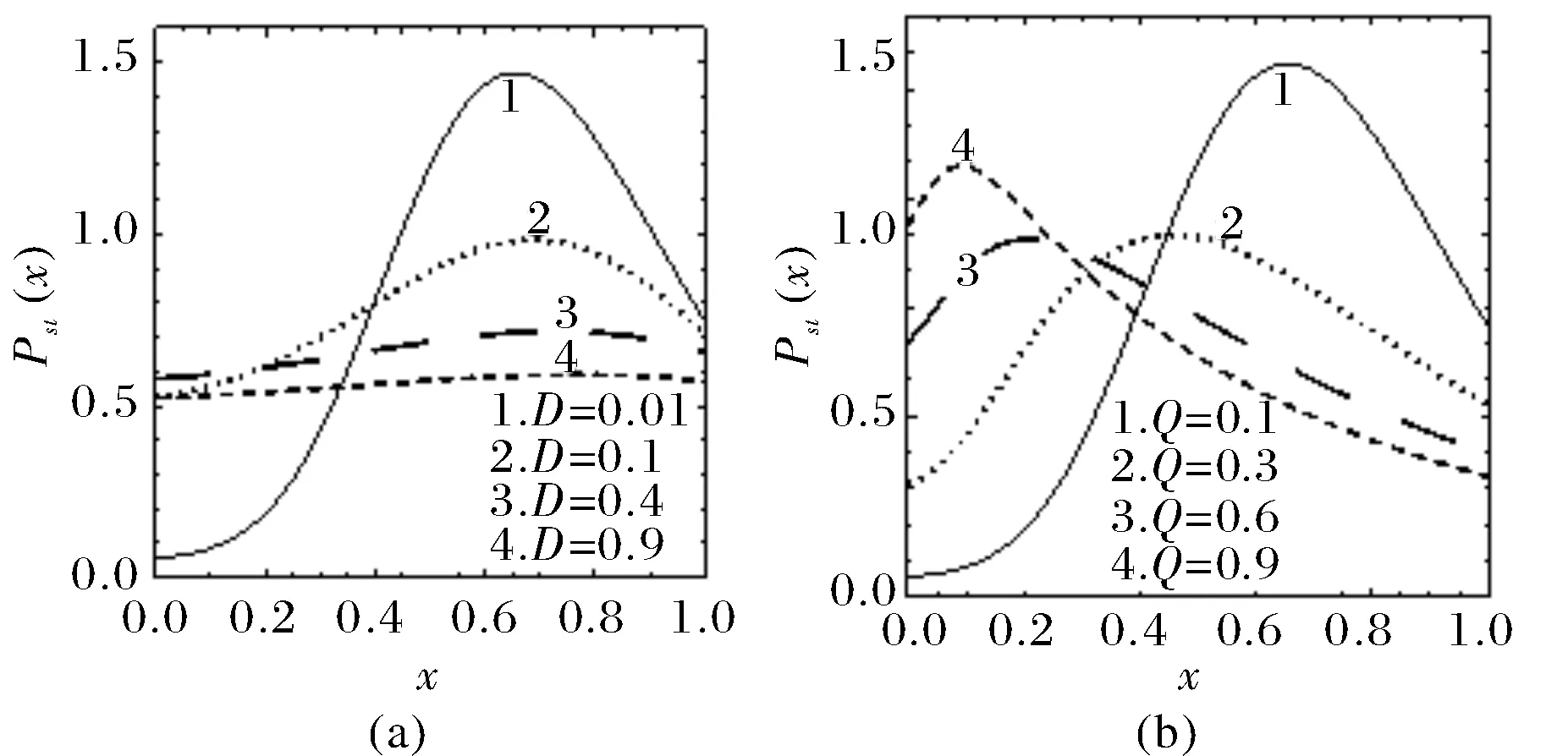
图1 Pst(x)作为x的函数Fig.1 Pst(x) as a function of x(其他参数c=0.8，τ=0.2，e=0.2，λ=0.3，(a)Q=0.1;(b)D=0.01)

通过对图1(b)可以看出：当乘性噪声强度Q逐渐增大的过程中，Pst(x)曲线的峰值会出现先降低，然后升高的变化趋势，且峰值的位置逐渐向x=0靠近.这种变化趋势表明：随着Q的增大，被占据的生境斑块的比例在峰值处的概率先减小，然后又增加，说明环境波动造成集合种群的不稳定性.这个过程可以增加集合种群的优胜劣汰，有利于对更好、更能适应环境变化的基因群的保留和延续.但是，峰值的位置逐渐向x=0移动，说明集合种群占据的空间在逐渐减小，即对集合种群的生存发展产生了不利的影响，因此可以得到：内部噪声强度的增加会导致集合种群的稳定性变弱.

2.2噪声间关联强强度对系统稳定性的影响

噪声间关联强度对系统稳定性的影响如图2(a)和(b)所示.从图2(a)可以看出，在正关联的情况下(0<λ<1)，Pst(x)曲线峰值的高度会随着|λ|的增大而逐渐的变大，也就是说被占据生境斑块的比值在峰值处的概率在不断变大；但是峰值的位置的变化相对较小，即被占据的生境斑块的比例在峰值处的概率基本不变，所以|λ|的增大强化了集合种群的稳定性.在负关联的情况下(-1<λ<0)，如图2(b)所示，随着|λ|的增加，Pst(x)曲线峰值的高度降低，这表明|λ|的增加弱化了集合种群的稳定性.综合可知，噪声间正关联时，|λ|的增加强化集合种群的稳定性；噪声间负关联时，|λ|的增加削弱集合种群的稳定性.

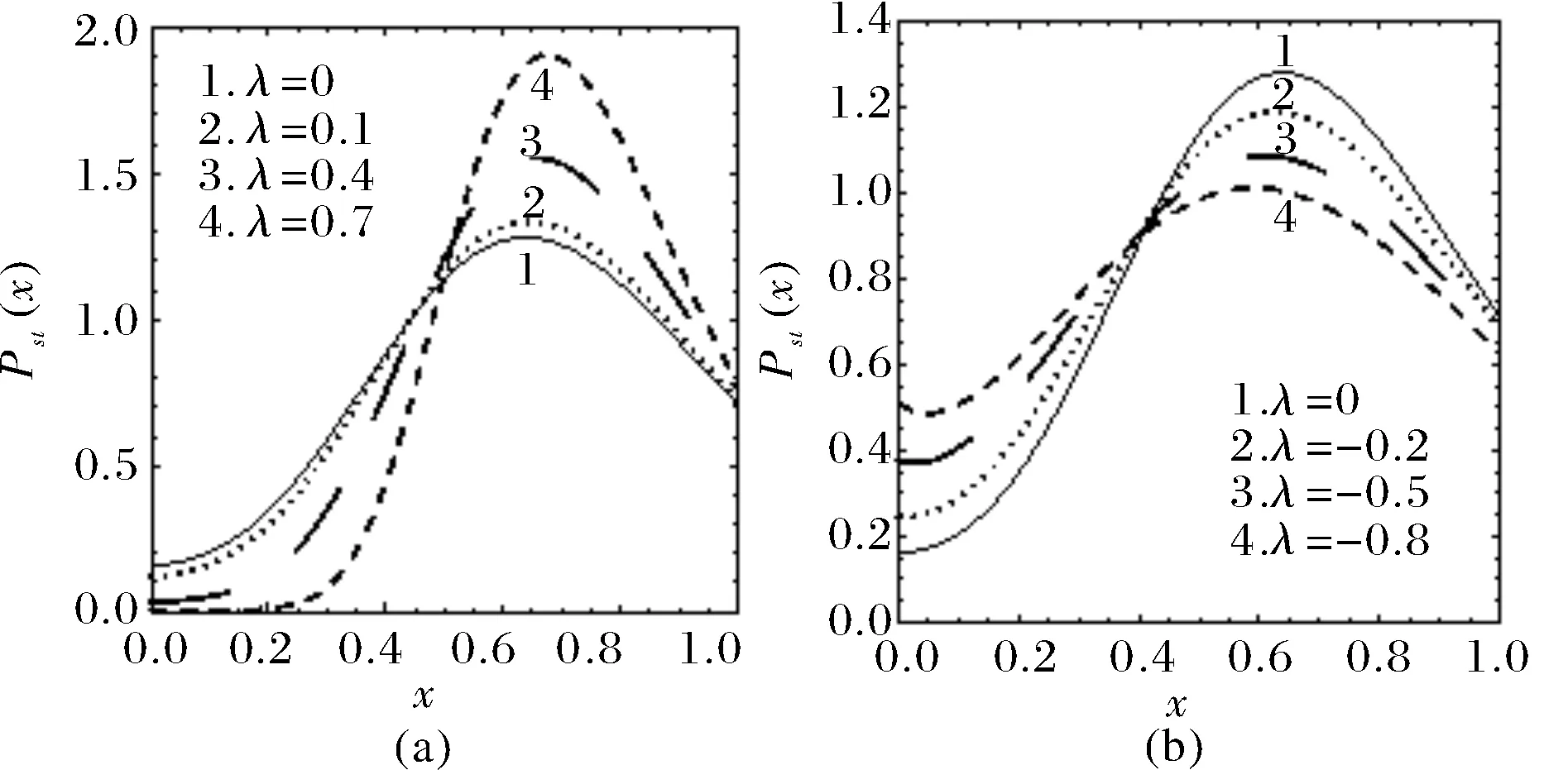
图2 Pst(x)作为x的函数Fig.2 Pst(x) as a function of x(其他参数c=0.8，e=0.2，τ=0.2，Q=0.1，D=0.01)

2.3色噪声色关联时间对系统稳定性的影响

图3绘制了Pst(x)随不同关联时间τ变化的图像.由图可知，随着τ的增加，Pst(x)曲线的峰值高度逐渐变大，且峰值的位置逐渐向右移动，这个现象表明被占据生境斑块的比值在峰值处的概率逐渐增加，即集合种群占据的生存空间增大，所以τ的增加强化了集合种群的稳定性，对集合种群稳定性产生有利的影响.

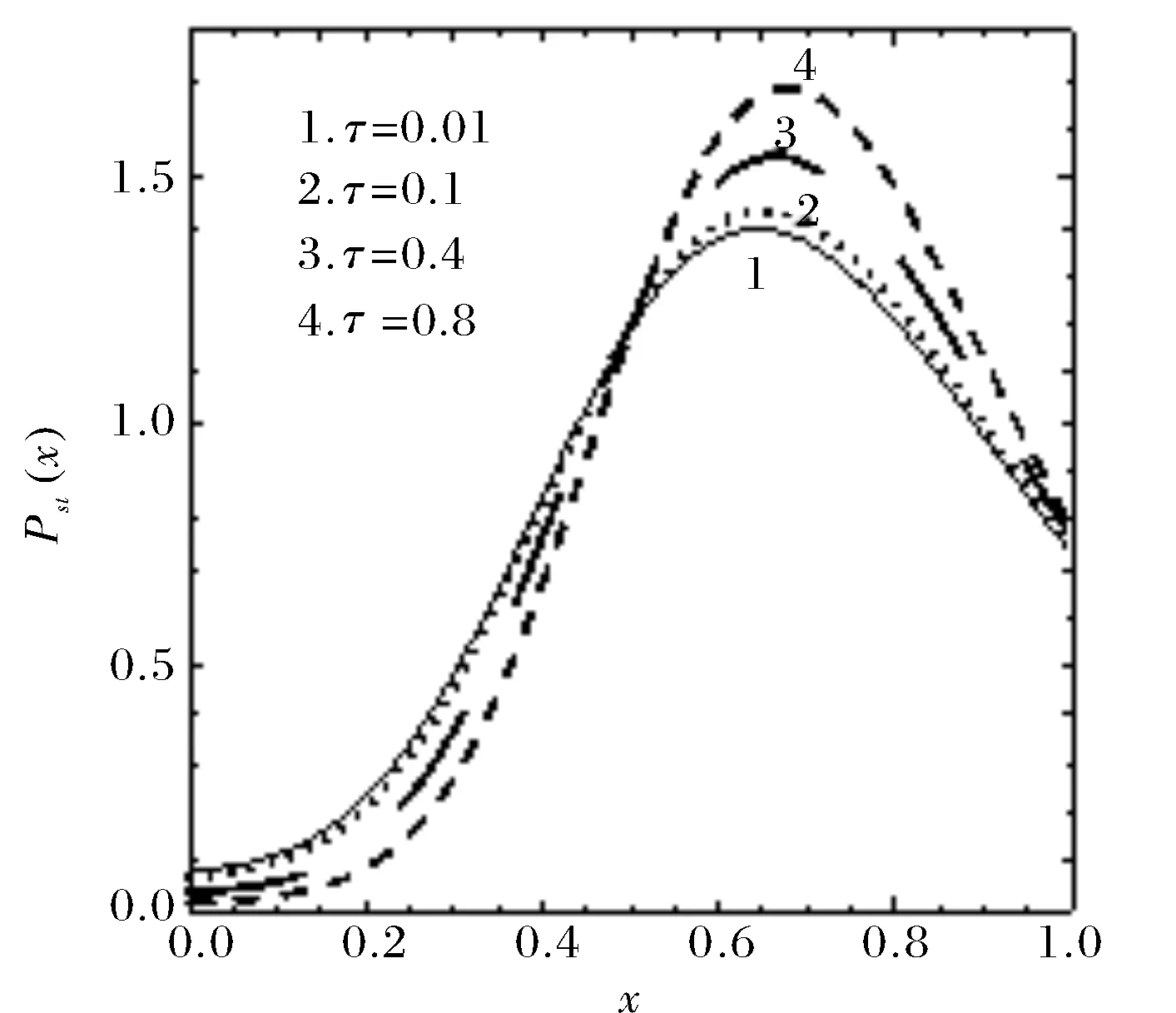
图3 Pst(x)作为x的函数Fig.3 Pst(x) as a function of x(其他参数c=0.8，e=0.2，λ=0.3，Q=0.1，D=0.01)

3噪声对系统平均灭绝时间的影响

根据平均首次通过时间的表达式(12)，可以作出平均灭绝时间T(xs→x0)的变化曲线.

3.1噪声强度对和关联时间平均灭绝时间的影响

图4给出了不同噪声关联时间下，平均灭绝时间T(xs→x0)作为Q的函数随着τ变化的曲线.从图4可以看出，当Q取值较小时，T(xs→x0)是Q的单调减函数，Q的增加会导致集合种群快速的从稳定态趋于灭绝态，符合图1(b)的描述.但是随着τ的增加，平均灭绝时间T(xs→x0)变大，对延缓种群灭绝起到积极作用，对集合种群的生存繁衍是有利的，这和图3是一致的.

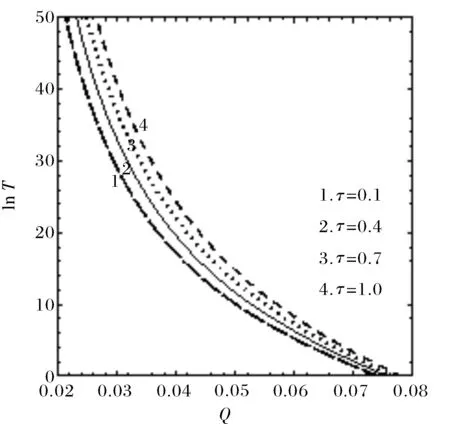
图4 平均灭绝时间T(xs→x0)与Q的函数关系(其他参数)Fig.4 The relationship between the mean extinction time T(xs→x0) and Q

3.2关联时间和关联强度对平均灭绝时间的影响

图5给出了在正、负关联两种情况下，平均灭绝时间T(xs→x0)随着噪声关联时间τ的变化曲线.综合图5(a)、(b)两图可知，T(xs→x0)是τ的单调增函数，即随着τ的增加，集合种群趋于灭绝的时间会增大，这表明集合种群系统的稳定性得到增强，对延缓集合种群灭绝起到积极作用.如图5(a)所示，在正关联的情况下(0<λ<1)，随着|λ|的增加，系统的平均灭绝时间T(xs→x0)增加，这说明集合种群趋于灭绝的时间延长，集合种群系统的稳定性得到了强化，对集合种群生长生存起到积极作用.在负关联的情况下(-1<λ<0)，如图5(b)所示，系统的平均灭绝时间T(xs→x0)随着|λ|的增加而减小，即集合种群的平均灭绝时间T(xs→x0)减小，加速了系统从稳定态xs向灭绝态x0转变，也就是说|λ|的增加弱化了集合种群系统的稳定性.

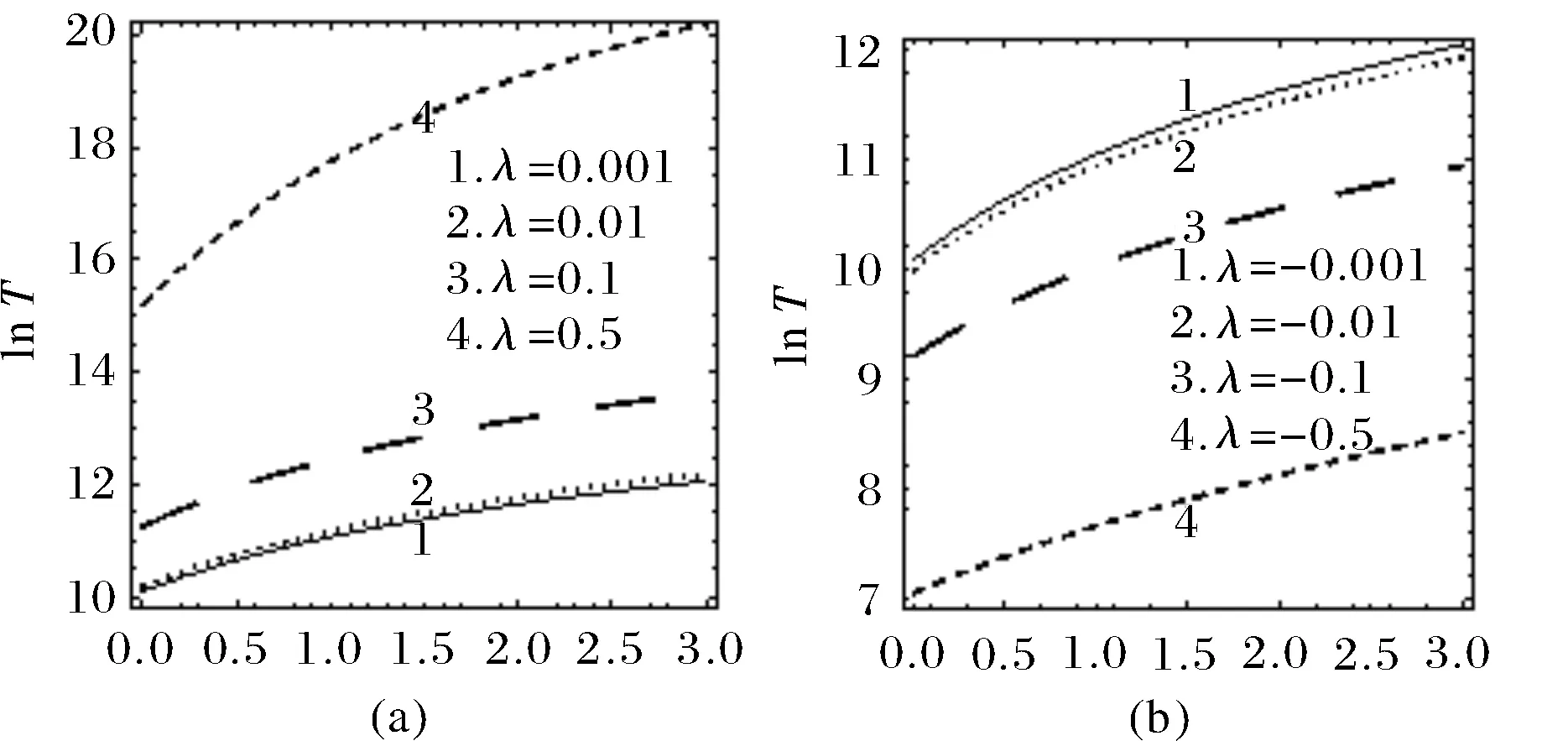
图5 平均灭绝时间T(xs→x0)与关联时间τ的函数关系Fig.5 The relationship between the mean extinction time T(xs→x0) and τ(其他参数c=0.8，e=0.2，Q=0.2，D=0.1)

4结论

在经典存在生境破坏集合种群Levins模型的基础上，本文通过引入外部环境随机波动和内部随机波动等噪声形式，重点讨论了色关联色噪声对集合种群稳定性和MFPT的影响，研究结果表明：

1) 加性噪声强度D的增加会弱化集合种群的稳定性，且乘性噪声强度Q的增大会对集合种群的稳定性产生不利影响；

2) 噪声间关联时间τ的增加使集合种群的稳定性得到强化；

3) 当噪声之间处于正关联时(0<λ<1)，|λ|的增加导致集合种群的稳定性得到强化；而负关联时(-1<λ<0)，|λ|的增加削弱集合种群的稳定性；

4) 平均灭绝时间T(xs→x0)是是Q的减函数，Q的增加会促使集合种群平均灭绝时间减小；.

5) T(xs→x0)是τ的单调增函数，τ的增加延缓了集合种群的灭绝.

[1] 王寿兵， 吴 峰， 刘晶茹. 产业生态学[M]. 北京：化学工业出版社，2005.

[2] OTSO O. Habitat destruction，habitat restoration and eigenvector-eigenvalue relations[J]. Mathematical Biosciences， 2003， 181(2):165-176．

[3] LEVINS R. Some demographic and genetic consequences of environmental heterogeneity for biological control[J]. Bulletin of the Entomological Society of America， 1969， 15: 237-240．

[4] HANSKI I， GILPIN M. Metapopulation biology: ecology， genetics and evolution[M]. London: Academic Press，1996．

[5] 周淑荣， 王 刚. 保护区的大小和数量效果的模拟研究[J]. 生态科学，2002， 21(3):193-196．

[6] SUSAN H. Local extinction in a metapopulation context: an empirical evaluation[J]. Biological Journal of the Linnean Society， 1991， 42(1-2):73-88．

[7] MOILANEN A， HANSKI I. Metapopulation dynamics: effects of habitat quality and landscape structure[J]. Ecology， 1998， 79(7):2503-2515．

[8] ALAN H， SUSAN H. Metapopulation dynamics and genetics[J]. Annual Review of Ecology and Systematics， 1994， 25:167-188．

[9] HANSKI I. Metapopulation dynamics[J]. Nature， 1998， 396(5): 41-49．

[10] 王参军， 李江城， 梅冬成. 噪声对集合种群稳定性的影响[J]. 物理学报，2012， 61(12)：120506-120506．

[11] 李江城， 梅冬成. 集合种群的延时效应[J]. 物理学报，2008， 57(11):6792-6798．

[12] 王康康， 刘先斌， 杨建华. 色交叉关联噪声作用下集合种群的稳定性和平均灭绝时间[J]. 物理学报， 2013， 62(10):100502-100502．

[13] 马祖飞， 李典谟. 种群统计随机性和环境随机性对种群灭绝的影响[J].生态学报，2003， 23(12): 2702-2710．

[14] 胡 岗. 随机力与非线性系统[M]. 上海: 上海科技教育出版社，1994: 23．

[15] JUNG P， HANGGI P. Dynamical systems: a unified colored-noise approximation[J]. Phys Rev A， 1987， 35(10): 4464-4466．

[16] WANG C J， CHEN S B， MEI D C. Steady-state analysis of a bistable system subject to a colored multiplicative noise and white additive noise with colored cross-correlated noises[J]. Chinese Physics， 2006， 15(7):1435-1440．

[17] 王国威， 徐大海， 程庆华. 关联噪声和周期信号驱动非对称双稳系统的稳态分析[J]. 量子电子学报，2014，31(1)：86-93．

[18] GARDINER C W. Handbook of Stochastic Methods， Springer in Synergetics[M]. Berlin: Springer-Verlag， 1983．

[19] HU G， DITZINGER T， NING C Z et al. Stochastic resonance without external periodic force[J]. Chinese Physics Letters， 1993， 71(6):807-810．

[20] VILAR J M G， RUBI J M. Stochastic multiresonance[J]. Chinese Physics Letters， 1997， 78(15):2882-288．

[21] MCNAMARA B， WIESENFELD K. Theory of stochastic resonance[J]. Physical Review A， 1989， 39(9): 4854-4868．

[22] 王国威， 程庆华， 徐大海. 关联噪声对集合种群稳定性和平均灭绝时间的影响[J].华中师范大学学报(自然科学版)， 2014， 48(2)：190-196．

[23] CASTROF J， KUPERMAN M N， FUENTES M et al. Experimental evidence of stochastic resonance without tuning due to non-Gaussian noise[J]. Physical Review E， 2001， 64 (5): 1051-1053．

[24] 王国威， 付 燕. 噪声在双稳和生物系统中非线性效应的应用研究[J].湖北理工学院学报， 2016， 32(3)：46-51．

[25] BARZYKIN A V， SEKI K. Periodically driven linear system with multiplicative colored noise[J]. Physical review E， 1998， 57 (6): 6555-6563．

[26] 王国威. 噪声作用下双稳系统和集合种群的统计性质研究[D]. 长江大学，2014．

[27] 杨慧涛， 吴玉敏， 张惠英. 毒素作用下两种群时滞竞争系统的捕获分析[J]. 福州大学学报(自然科学版)， 2012(5): 557-562．

[28] JIA Y， LI J R. Transient properties of a bistable kinetic model with correlations between additive and multiplicative noises: Mean first-passage time[J]. Phys Rev E， 1996， 53(6): 5764-5768．

[29] 王国威， 程庆华， 徐大海. 色关联噪声对林木Logistic生长模型的影响[J]. 物理学报， 2013， 62(22)：224208-224208．

Effects of cross-correlated colored-noises on the mean extinction time and stability of a metapopulation

WANG Guowei1，2

(1.Department of Basic Courses， Nanchang Institute of Science & Technology， Nanchang 330108;2.Key Laboratory of Nonlinear Mechanics， Nanchang Institute of Science & Technology， Nanchang 330108)

The concept of the metapopulation system was previously introduced by Levins. After that, many researchers have been studying in the field of metapopulation system based on the Levins model. However, most studies are limited to deterministic Levins model and white noises. In the paper, the mean extinction time and stability of a metapopulation system subjected to cross-correlated Gaussian colored noises are investigated based on the Levins model. By means of a unified colored-noise approximation approach (UCNA) and mathematical analysis, the Approximate Fokker-Planck equation (AFPE) of the Levins model is obtained, and the stationary probability distribution function (SPDF) is obtained by solving the FPE. And then, the analytical expression of the mean first-passage time (MFPT) of the Levins model is derived by using the steepest descent method. The numerical computations show that: 1) The additive noise and the multiplicative noise intensity weaken the stability of metapopulation; 2)τenhances the stability of metapopulation; 3) in the case of 0<λ<1, the stability of the metapopulation is enhanced when the is |λ|increasing, but the stability is weakened in the case of -1<λ<0 as |λ| increasing; 4) the mean extinction timeT(xs→x0) is a decreasing function ofQ; 5) The mean extinction timeT(xs→x0) is an increasing function ofτ.

Levins model; metapopulation; colored-noises; extinction; stability

2016-03-11.

江西省教育厅科学技术研究项目( GJJ151240); 南昌工学院科技课题(No.GJKJ-15-34); 南昌工学院教学改革课题(NGJG-2015-67)和南昌工学院非线性力学重点实验室资助项目.

1000-1190(2016)06-0831-05

O415

A

*E-mail: 501284253@qq.com.