基于观测器方法的复杂网络混沌系统的有限时间同步控制
2016-12-22毛北行孟晓玲
毛北行, 孟晓玲
(郑州航空工业管理学院 理学院, 郑州 450015)
基于观测器方法的复杂网络混沌系统的有限时间同步控制
毛北行*, 孟晓玲
(郑州航空工业管理学院 理学院, 郑州 450015)
基于Lyapunov稳定性理论,利用观测器方法研究了复杂网络系统的有限时间混沌同步问题,研究表明,通过设计适当的控制器,能够使复杂网络的主从系统达到有限时间同步,数值算例表明该方法的正确性.
观测器方法; 有限时间; 混沌同步
复杂网络广泛地存在于自然界,并取得了很多结果[1-5]. 在实际工程中,往往要求控制系统的轨迹不超出一定的界限.该问题引起了控制界的高度关注[6-10],文献[11]讨论了Lurie混沌系统的有限时间同步问题,并估计出了系统取得同步的所需时间,文献[12]研究了基于Terminal滑模控制的有限时间同步问题,文献[13]研究了带有不确定和外部扰动的Duffling混沌系统的有限时间同步问题,文献[14]研究了具有死区输入的分数阶混沌系统的有限时间同步问题,文献[15]研究了一类复杂网络混沌系统的有限时间混沌同步问题,本文利用观测器方法研究了复杂网络系统的有限时间混沌同步问题,研究表明,通过设计适当的控制器,能够使复杂网络的主从系统达到有限时间同步,数值算例表明该方法的正确性.
1主要结果
考虑如下复杂网络混沌系统:

(1)
yi(t)=Cixi(t),
(2)
其中,xi=(xi1,xi2,…,xiN)T∈RN是网络中节点i的状态向量,fi:RN→RN为非线性函数,Q(t)为内部耦合矩阵,A(t)=(aij(t))N×N为外部耦合矩阵,在t时刻满足:aij(t)=aij≠0,表示在t时刻从节点i到j有一条耦合强度为aij=aij(t)的连接边,并且在任何时候满足
系统(1)(2)对应的观测系统为:

i=1,2,…,N,
(3)
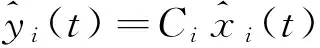
(4)
以系统(1)、(2)为主系统,设计观测系统(3)、(4)作为从系统,定义系统误差为:
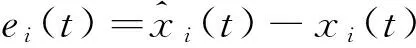
则容易得到:

引理1[16]考虑如下n维方程

(5)
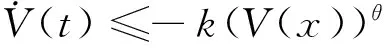
引理2[17]设a1,a2,…,an>0,0

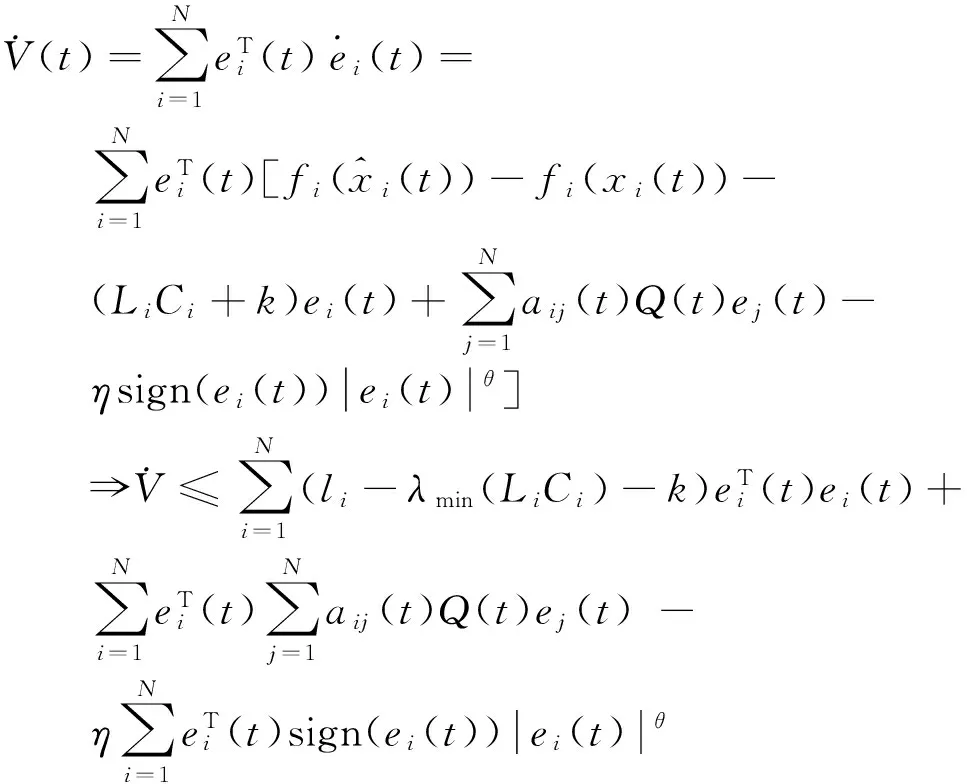
根据下面不等式:
而
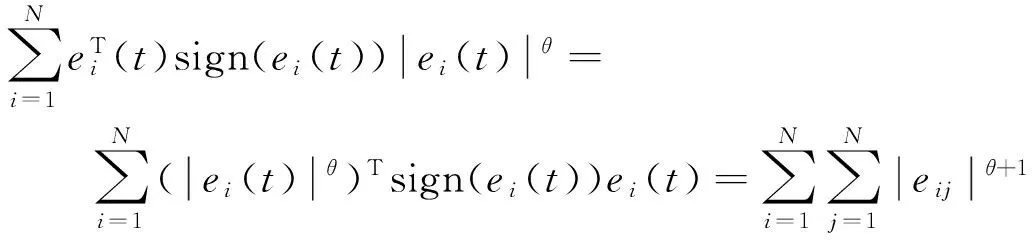
由引理2,可得:

从而很容易得到:

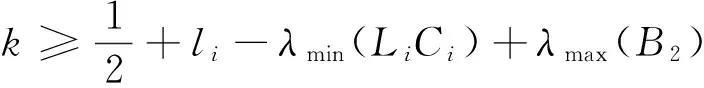
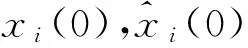
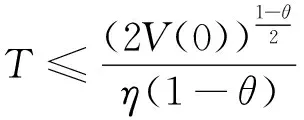
证明以系统(1)、(2)为驱动系统,对应的观测系统(3~4)作为响应系统,定义系统误差为:
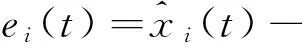
则容易得到:
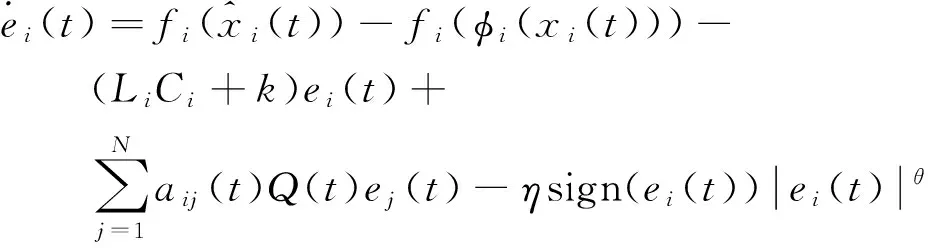
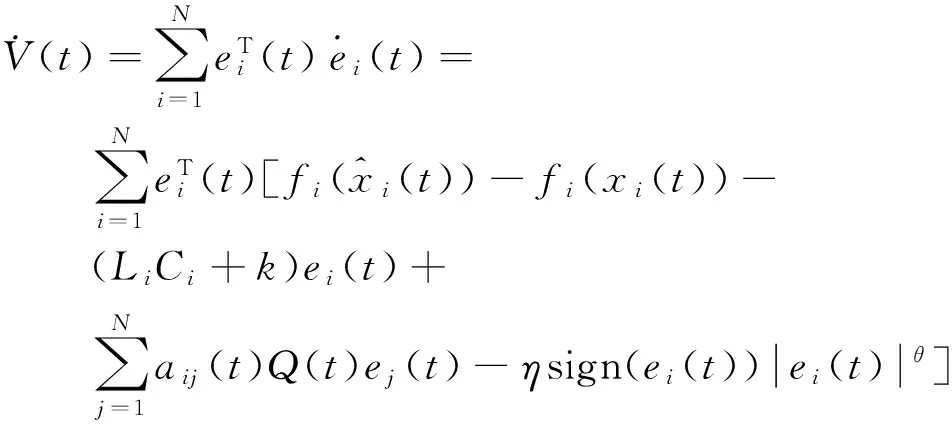
下面的证明过程类似于定理1,很容易得到:
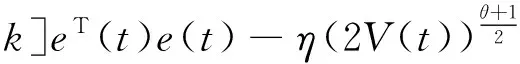
考虑如下复杂网络混沌系统:

(6)
yi(t)=Cixi(t),
(7)
其中,光滑非线性函数fi(·)满足假设1,H(xj(t))为光滑的非线性函数,满足如下假设:

(8)
系统(6)(7)对应的观测系统为:

(9)
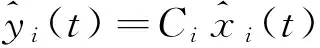
(10)
以系统(6)、(7)为主系统,设计观测系统(9)、(10)作为从系统,定义系统误差为:
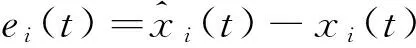
则容易得到:


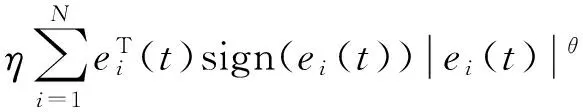
下面的证明类似定理1.
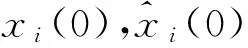
假设3非线性向量函数满足条件:

假设4H(xj(t))为光滑的非线性函数,满足:

证明以系统(6)、(7)为主系统,设计观测系统(9)、(10)作为从系统,定义系统误差为:
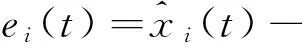
则容易得到:

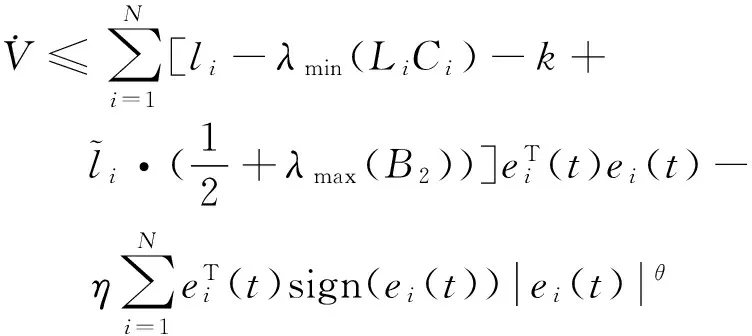
下面的证明类似定理3,略.
2数值算例
以N=3的Lorenz系统为例:

时具有混沌吸引子.
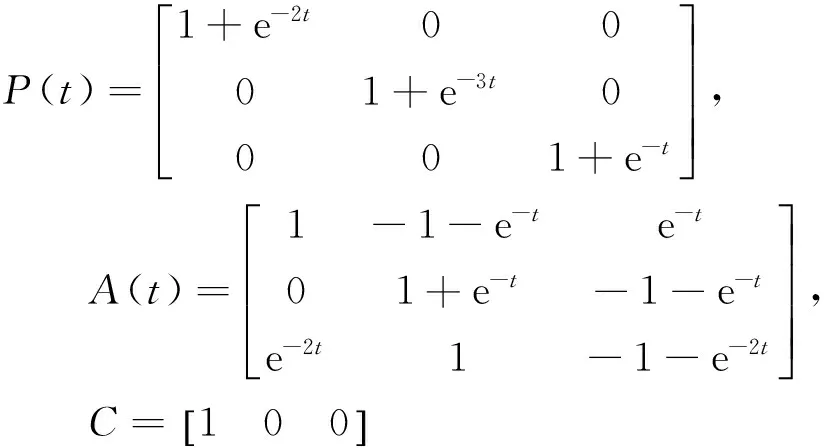
定理1中l=0.8,η=3,θ=0.6,k>0.737+λmax(B2);
定理2中l=0.8,η=3,θ=0.6,k>0.748+λmax(B2);

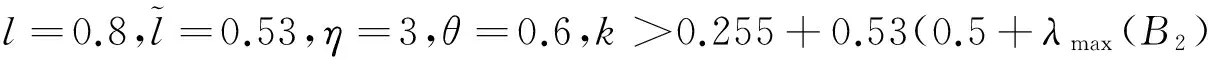
定理1~4中计算得到的观测矩阵分别为

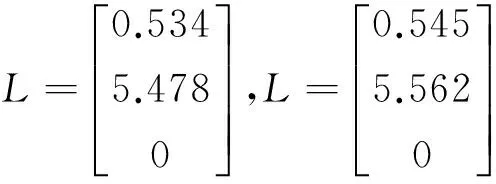
定理1~4中系统的误差曲线分别对应于图1~图4,其中,横纵轴单位分别为s和m.

图1 定理1中的系统误差Fig.1 The errors of systems in theorem 1

图2 定理2中的系统误差 Fig.2 The errors of systems in theorem 2

图3 定理3中的系统误差Fig.3 The errors of systems in theorem 3

图4 定理4中的系统误差Fig.4 The errors of systems in theorem 4
3结论
利用观测器方法研究了复杂网络系统的有限时间混沌同步问题,根据Lyapunov稳定性理论和有限时间同步的相关知识给出了主从系统取得观测器同步的充分性条件.并把该结论作了进一步推广.
[1] 吕 翎, 李 纲, 张 檬. 等. 全局耦合网络的参数辨识与时空混沌同步[J]. 物理学报,2011, 60(9):5051-5056.
[2] 李德奎, 张建刚.时滞和非时滞耦合的驱动响应动态网络的函数投影同步[J].太原理工大学学报,2013,44(2):162-168.
[3] 卞秋香, 姚洪兴. 复杂网络的线性广义同步[J].系统工程理论与实践,2011, 31(7):1334-1340.
[4] LYU L, LI G,GUO Y . Generalized chaos synchronization of a weighted complex network with different nodes[J]. Chinese Phys B,2010, 19(8):5071-5077.
[5] AMATO F, ARIOLA M, COSENTINO C,et a1.Necessary and sufficient conditions for finite—time stability of linear systems[J].Proc of 2003 American Control Conference,2003(5):4452-4456.
[6] AMATO F, ARIOLA M, COSENTINO. Control of linear discrete-time systems over a finite-time interval[C]//43rd IEEE Conference on Decision and Control,Atlantis:IEEE Press, 2004:1284-1288.
[7] AMATO F. Finite-time control of discrete-time linear system[J].IEEE Trans Automat Control,2005, 50(5):724-729.
[8] DORATO P. Short time stability in linear time varying system[C]//Proc International Convention on Record Part 4, 1961:83-87.
[9] AMATO F, ARIOLA M, ABDALLAH C T,et al .Danamic output feedback finite-time control of LTI Systems subject to parametric uncertainties and disturbances[C]//Proc European Control Conference,Kals-ruhe 1999:1176-1180.
[10] AMATO F,AROLIA M,DOBATO P.Finite-time control of linear systems subject to parametric uncertainties and disturbance[J].Automatic, 2001, 37:1459-1463.
[11] 毛北行, 李巧利. Lurie混沌系统的有限时间同步问题[J].四川师范大学学报(自然科学版), 2014, 37(4):497-500.
[12] 王校锋, 司守奎, 史国荣. 基于Terminal滑模的有限时间混沌同步实现[J].物理学报, 2006, 55(11):5694-5699.
[13] 徐瑞萍, 高存臣. 不确定Duffling混沌系统的有限时间同步[J].青岛科技大学学报, 2015, 35(3):350-354.
[14] 田小敏, 费树岷, 柴 琳. 具有死区输入的分数阶混沌系统的有限时间同步[J].控制理论与应用, 2015, 32(9):1240-1245.
[15] 毛北行, 王战伟. 一类分数阶复杂网络系统的有限时间同步控制[J].深圳大学学报理工版, 2016, 33(1):96-101.
[16] BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomuous systems[J]. SIAM J Control Optim, 2000, 38(3): 751-766.
[17] HARDY G, LITTLEWOOD J, POLYA G. Inequalities[M]. Cambridge: Cambridge University Press,1952.
Finite-time synchronization control of complex networks chaos systems based on observer approach
MAO Beixing, MENG Xiaoling
(College of Science, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015)
The paper studied the problem of finite-time synchronization control of complex networks chaos systems based on Lyapunov stability theory using observer approach . The proof illustrate that the master-slave systems is chaos synchronization under proper controller. Numerical simulations example of chaotic system verify the correctness of the proposed method.
observer approach; finite-time; chaos synchronization
2016-06-22.
国家自然科学青年基金项目(NSFC11501525);河南省高等学校青年骨干教师资助计划项目(2013GGJS-142).
1000-1190(2016)06-0826-05
O193
A
*E-mail: bxmao329@163.com.
