基于双层复形法的重力坝断面优化研究

李 斌，杨 杰,2

(1 西安理工大学 水利水电学院，陕西 西安 710048；2 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)



基于双层复形法的重力坝断面优化研究

李 斌1，杨 杰1,2

(1 西安理工大学 水利水电学院，陕西 西安 710048；2 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)

【目的】 进行重力坝断面优化设计的算法研究，为减小重力坝断面面积，优化重力坝体型提供参考。【方法】 以复形法为基础，简化了在所有约束条件下寻找可行点的收缩步骤以减少计算次数，然后构造了双层优化结构，即把第1层复形的优化结果作为第2层复形的初始点，再以复形法原理进行优化，最后以某拟建重力坝为实例进行了坝体横断面的优化分析。【结果】 优化后的各断面特征参数均满足要求，其断面面积较原设计方案减小了15.97%，坝体体型更瘦，且坝体上、下游应力分布更加合理。【结论】 双层复形法较复形法具有更高的稳定性、更快的收敛速度，可适用于大体积、结构复杂的水工结构优化设计。

水工结构；混凝土重力坝；断面优化； 双层复形法

我国有大量在建或拟建的实体重力坝，其体积庞大、修建成本高，如何进行结构断面优化设计对重力坝的施工进度和成本控制具有非常重要的意义[1-3]。目前，较为普遍的结构优化算法有蚁群算法、模拟退火算法、粒子群算法和复形法等，且都取得了不错的效果[4-6]。但蚁群算法是离散算法，求解连续问题需要离散化，且容易出现停滞现象，不利于寻找全局最优解。模拟退火算法的参数选取亦比较困难，参数选取不当会导致退火不充分，继而导致算法全局搜索能力很低。在解决多峰优化问题时，粒子群优化算法比较容易陷入局部最优值，从而无法找到真正的全局最优值。复形法(Complex Method，CM)可以在m维受非线性约束的设计空间内构造一个具有k个顶点的多面体，不断选择更好点代替最坏点，是解决约束最优化问题的一种直接搜索方法[7]。影响其优化能力的主要原因有以下3点：一是由于复形中包含的顶点多样性不足，导致寻优的范围只能在关于最坏点的直线上。李亮等[8]在各个顶点的寻优直线上分别寻求比各自顶点有所改善的新复形点，构成多个新复形并选择复形顶点多样性最大的作为下一次迭代的初始复形，其还利用蚁群算法求出的较优解代替复形顶点中基因型相似的顶点，来增强复形法的搜索能力[9]。二是由于随机生成的复形或计算过程中构成的新复形所包围的域不够大，容易产生局部最优。莫愿斌等[10]、张敏辉[11]和张鲁明[12]通过粒子群算法进行搜索之后，对当前种群最优粒子的最好位置和此粒子的历史最好位置再进行复形法的局部搜索，来提高整个算法的寻优能力。三是复形法容易陷入局部最优而无法跳出。陈昌富等[13]引入退火机制来跳离局部极优，给复形法再一次寻找全局最优的机会，进而继续用复形法来搜索。

以上对复形法的改进主要是增加算法本身或与其他算法结合，实现过程复杂且计算次数较多。复形法原本简单可靠、理论成熟、应用广泛，本研究在原本复形法的基础上，分析了其运算结构并进行双层复形法(Double-Layer Complex Method，DLCM)的优化程序设计，最后通过实例验证该算法有一定的优化能力且优化结果合理，以期为重力坝断面优化设计提供参考。

1 重力坝断面优化数学模型

重力坝断面优化方法较多[14-16]，数学模型主要包括设计变量、目标函数和约束条件。

1.1 设计变量

设计变量X1、X2、X3分别为上游垂直面距离、上游坡率和下游坡率，如图1所示，其中H为大坝总高度，B为坝顶宽度，L为大坝下游垂直面距离。

图 1 重力坝设计断面中的变量

1.2 目标函数

如图1所示，取单位宽度的坝体断面面积W作为目标函数，可表示为：

W=HB+(H-X1)2X2/2+(H-L)2X3/2。

(1)

1.3 约束条件

1.3.1 几何约束 设计变量X1、X2、X3的几何约束条件为：

X1:H/3≤X1≤2H/3;

X2:0≤X2≤0.2;

X3:0.5≤X3≤0.9;

0≤Xi;(i=1,2,3)。

1.3.2 稳定约束 抗滑稳定安全系数应大于规定的安全系数，参照《混凝土重力坝设计规范》(SL 319-2005)，在基本荷载组合下确定安全系数的约束条件为：

(2)

式中：K′为抗剪断强度公式计算的安全系数；[K′]为允许安全系数；f′为坝体混凝土与坝基接触面的抗剪断摩擦系数；∑W′为接触面以上的总铅直力，kN；U为作用在接触面的扬压力，kN；c′为坝体混凝土与坝基的抗剪断凝聚力，kPa；A′为坝基接触面面积，m2；∑P为接触面以上的总水平力，kN。

1.3.3 应力约束 参照《混凝土重力坝设计规范》(SL 319-2005)，在基本荷载组合下坝踵不出现拉应力、坝趾应力应不大于坝基容许压应力，由此可得：

(3)

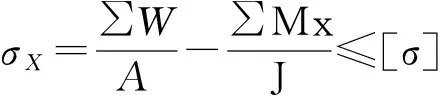
(4)

式中：σS、σX分别为坝踵、坝趾的垂直应力之和，kPa；[σ]为容许压应力，kPa；∑W为作用于坝段上或1 m坝长上全部荷载在坝基截面上法向力的总和，kN；∑M为作用于坝段上或1 m坝长上全部荷载对坝基截面形心轴的力矩总和，kN·m；A为坝段或1 m坝长的坝基截面积，m2；x为坝基截面上计算点到形心轴的距离，m；J为坝段或1 m坝长的坝基截面对形心轴的惯性矩，m4。

2 双层复形法

CM详细内容见文献[4]，其程序设计流程见图2[17]。图2中虚线框外主要是形成初始复形点的过程，框内为复形优化搜索的过程。图2中：k为复形的顶点数；ε为目标函数迭代精度终止的条件值，是一个很小的正数；ζ为终止反射系数的条件值，也是一个很小的正数；s为复形点中可行点的数量；XL、XG和XR分别为复形顶点中的最好点、次好点和最坏点；F(Xα)、F(XR)分别为Xα、XR的目标函数值。针对CM本身存在的不足，本研究对复形点和双层复形结构进行了改进和优化。

赵东方 男，1995年生于云南昆明，现为西安交通大学计算机系硕士研究生.主要研究方向为FPGA性能优化.

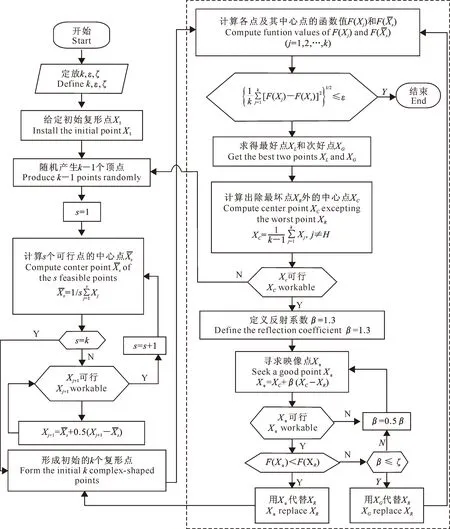
图 2 复形法程序设计流程图[17]

2.1 复形点的改进

复形法形成初始复形点的方法是首先人为给定一个可行点，再用(5)式随机形成其余点。

(i=1,2,…,n;j=1,2,…,k)。

(5)

式中：i为变量号；j为复形顶点号；ai、bi分别为设计变量的上、下限；R为0～1的随机数，可由计算机自动产生。

(6)

初始复形点的形成至关重要[18-20]，当人为给定的初始复形点不可行时，则会影响对其他复形点的判断，导致计算失败；对其余点逐一判断，每次收缩之后需再一次判断是否为可行点，计算过程比较复杂。

本研究应用Matlab语言编写了子程序Fea、Jud和Opt。Fea以几何约束为条件，用来产生一个指定上、下限的随机复形点，省略了人为定义初始复形点的步骤；Jud以所有约束为条件，用来判断该点在满足几何约束条件的同时是否也满足其他约束条件，即是否为一个可行点，这样形成的复形点全部为可行点，排除了人为顶点的影响，且省略了(6)式的收缩计算；Opt是以图2中虚线框中的内容为核心的优化程序，在主程序中每调用一次该程序，则找到一个更优的复形点来代替之前复形点中最坏的点。这3个程序是主程序的重要组成部分，主程序中除定义一些初始常量以外，利用这3个程序就可以很方便地进行优化。

2.2 双层复形结构的优化

形成初始复形后，选择最坏点XR，再用(7)式在XR与XC的连线上作α倍的映射，得到更优的映像点Xα，进而不断用Xα代替复形的最坏点XR，进行优化计算。

Xα=XC+β(XC-XR)。

(7)

式中：XC为除XR点外其余顶点的中心点。

每次改进复形点后以(8)式为收敛的判别准则，如满足式(8)，则迭代计算结束，此时复形各定点目标函数值最小的点即为最优解X*。

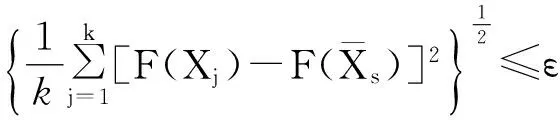
(8)

初始复形点的随机性使得复形的搜索域差异较大，进而导致搜索能力的较大差异；当面对多峰极值的优化问题时，单个复形容易陷入局部最优点。

双层复形结构[21]是假设复形顶点数k=2n时，n是几何约束的个数，首先形成第1层的n个复形，对它们优化固定次数之后，取出各个复形的最好点和次好点，再由这些点形成第2层复形，完成剩下的迭代计算。n个复形增强了复形顶点的多样性，扩大了搜索域，也避免了单个复形易陷入局部最优而无法跳出的缺陷。DLCM程序设计流程见图3。

3 优化设计的实例验证

3.1 工程概况

某拟建重力坝坝高40.5 m，设计水位高38 m，泥沙淤积高10.0 m，下游起坡点距坝顶8.0 m，下游水位2 m，坝顶宽5 m。扬压力折减系数α为0.3，水的容重为10 kN/m3，泥沙浮容重为8 kN/m3，内摩擦角为32°，混凝土容重为24 kN/m3，摩擦系数f′为0.75，凝聚力为550 kPa。在基本荷载工况下迭代精度条件ε和ζ均取0.000 1，DLCM中第1层迭代计算20次，之后为第2层优化计算，20组的平均优化结果与原始设计的坝体特征参数见表1。

3.2 优化结果分析

比较优化前后的坝体特征参数(表1)可以看出，优化之后的断面整体偏瘦，坝体断面面积比原设计方案减小了15.97%。重力坝断面下游坡率通常为0.6～0.8，这是经过大量实际工程经验获得的较为安全的参数，而本研究选取的下游坡率为0.5～0.9，目的是为了在基本荷载组合工况下寻求理论上的最优目标，其结果为0.552 9，说明规范中的 0.6～0.8在一般情况下是安全、合理的。该算法是在满足所有约束条件下寻求的最优目标，本例中的安全系数约束条件按重力坝设计规范取为3，其优化结果也为3，说明安全系数是控制重力坝断面的一个重要条件，如果希望断面更优，安全系数就会小于3，大坝就会不安全，其比原始设计的安全系数3.5小，说明原始设计的安全系数有一定的富余，特殊荷载组合下可选择安全系数约束条件为2.5，其优化过程依然适用。与原始的上、下游坝面应力进行比较，可知优化之后的上游压应力更小，下游压应力更大，且均有一定富余，这更符合重力坝的应力分布规律。

图 3 双层复形法程序设计流程图

表 1 优化前后坝体的特征参数

表2为CM和DLCM的20组重力坝断面优化结果，其中目标函数值W较为接近，说明复形法本身具有较强的寻优能力，但DLCM的计算次数更少，即计算效率更高。对目标函数和迭代次数的标准差而言，DLCM较CM降低了96.67%和37.5%，即该算法的计算稳定性更强。图4和5是其20组计算结果的对比，为了更清楚地看到目标函数值的差异，将优化结果统一减小了525 m2，只比较有差异的小数部分。由图4和5可见，DLCM的目标函数接近于水平直线，且迭代次数比CM整体偏少。因此可以断定，DLCM的计算稳定性和搜索效率较CM都有明显的提高。

表 2 CM和DLCM优化结果的比较

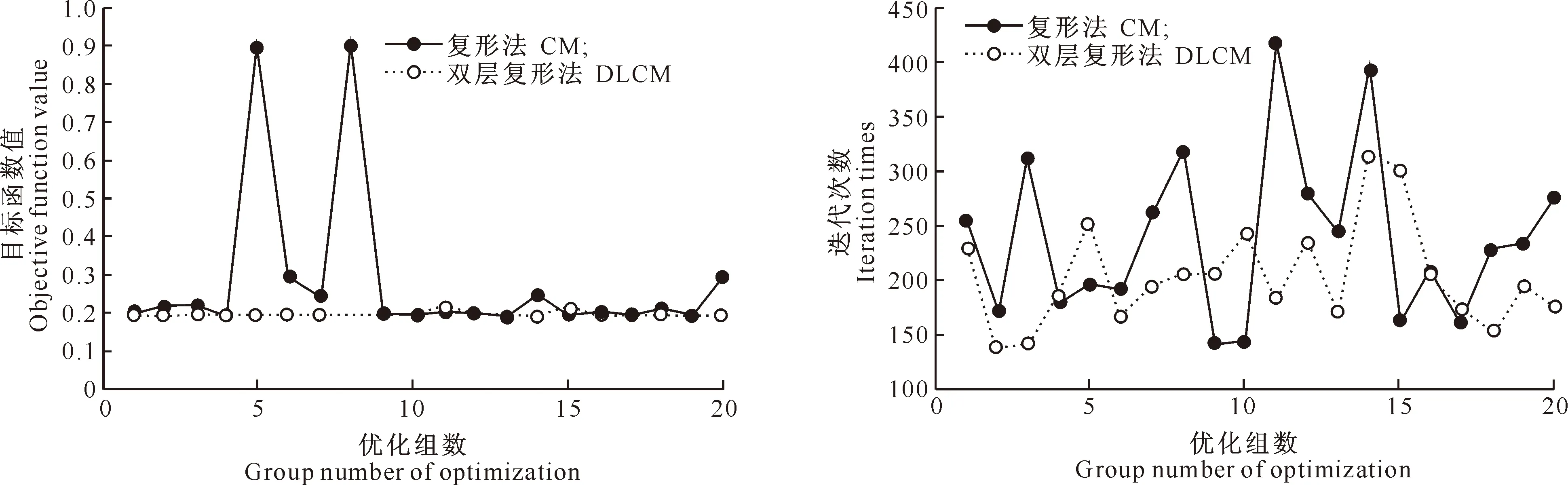
图 4 CM和DLCM优化结果的对比

图 5 CM和DLCM迭代次数的对比

图6为CM与DLCM的一次计算过程，同样对优化结果进行了放大处理。由图6可见，复形法的迭代计算在前几次收敛较快，以后逐次变慢，虽然双层结构的复形数有所增加，但最终迭代次数并没有增加，反而有所减少。双层复形法第1层以3个复形来搜索，扩大了搜索范围，当这3个复形最后收缩结果较为相近时，说明这个点是全局最优的可能性更大，反之则可防止某个复形陷入局部最优；第2层复形点由第1层复形点的优化结果形成，所以在20次优化之后，3个复形过程变为1个，这样就减小了由于初始复形点的随机性带来的影响，增强了复形法计算的稳定性。

图 6 迭代次数与目标函数值的关系

4 结 语

水工结构体积大、造价高，合理的优化可以节省造价。复形法简单可靠、理论成熟、应用广泛，是一种很好的水工结构优化设计方法。本研究对复形法进行了改进，并且应用Matlab进行了优化程序设计，程序具有较高的冗余度。由重力坝断面实例优化结果可知，双层复形法具有更高的搜索效率以及更强的计算稳定性，该算法可应用于水工结构的优化设计，为重力坝的断面优化设计提供了重要的参考。

本研究计算实例的优化过程相对简单，当遇到复形点更多、约束条件更复杂的问题时，应能更显著地反映出改进方法的优势。

值得指出的是，针对较为复杂的优化问题，可以尝试扩大第1层复形的个数，来增大搜索全局最优的概率，亦可以研究收缩系数对优化过程的影响，或许可以更有效地找到全局最优结果。

[1] 颜宏亮，闫 滨．水工建筑物 [M].北京：中国水利水电出版社，2012：15-71．

Yan H L,Yan B.Hydraulic structures [M].Beijing:China Water & Power Press,2012:15-71.

[2] 马红丽．重力坝剖面优化设计软件开发 [D].陕西杨凌：西北农林科技大学，2008．

Ma H L.The software development about optimum design of profile of gravity dam [D].Shaanxi，Yangling:Northwest A&F University,2008.

[3] Guan Q.Optimized program design of gravity dam section [J].Procedia Engineering,2012,28(1):419-423.

[4] 王广宇，解建仓，张建龙．基于改进蚁群算法的供水管网优化计算 [J].西北农林科技大学学报(自然科学版)，2014，42(1)：228-234．

Wang G Y,Xie J C,Zhang J L.Optimization of water supply network based on improved ant colony algorithm [J].Northwest A&F University(Nat Sci Ed),2014,42(1):228-234.

[5] 潘海琳．高拱坝体型优化决策系统研究 [D].南京：河海大学，2006．

Pan H L.Research on decision-making system of optimization design for high arch dam shape [D].Nanjing:Hohai University,2006.

[6] 刘 逸．粒子群优化算法的改进及应用研究 [D].西安：西安电子科技大学，2012．

Liu Y.Improvements and applications of particle swarm optimization algorithm [D].Xi’an:Xidian University,2012.

[7] 朱杰江．建筑结构优化及应用 [M].北京：北京大学出版社，2011：100-102．

Zhu J J.Building structure optimization and its application [M].Beijing:Peking University Press,2011:100-102.

[8] 李 亮，迟世春，林 皋．保持顶点多样性的复合形法及其在边坡稳定分析中的应用[J]．计算力学学报，2006，23(3):363-367．

Li L,Chi S C,Lin G.Complex method based on the maintenance of the diversity of the apex and its application to the slope stability analysis [J].Chinese Journal of Computational Mechanics,2006,23(3):363-367.

[9] 李 亮，迟世春，林 皋．基于蚁群算法的复合形法及其在边坡稳定分析中的应用 [J].岩土工程学报，2004，26(5)：692-696．

Li L,Chi S C,Lin G.The complex method based on ant colony algorithm and its application to the slope stability analysis [J].Chinese Journal of Geotechnical Engineering,2004,26(5):692-696.

[10] 莫愿斌，徐水华．带有复形法局部搜索的粒子群算法求解最优控制问题 [J].计算机应用研究，2011，28(7)：2506-2507．

Mo Y B,Xu S H.Particle swarm optimization with complex local searching for solving optimal control [J].Application Research of Computers,2011,28(7):2506-2507.

[11] 张敏辉．复形法粒子群优化算法研究 [J].计算机应用研究，2012，29(2)：464-468．

Zhang M H.Novel particle swarm optimization algorithm based on complex method [J].Application Research of Computers,2012,29(2):464-468.

[12] 张鲁明．基于粒子群和改进复合形法的边坡稳定分析 [D].辽宁大连：大连理工大学，2009．

Zhang L M.Slope stability analysis based on particle swarms complex method and improved complex method [D].Liao-ning，Dalian:Dalian University of Technolog,2009.

[13] 陈昌富，吴子儒，龚晓南．复合形模拟退火算法及其在水泥土墙优化设计中的应用 [J].岩土力学，2007，28(12)：2543-2548．

Chen C F,Wu Z R,Gong X N.Complex simulated annealing and its application to optimization design of cement-soil retaining walls [J].Rock and Soil Mechanics,2007,28(12):2543-2548.

[14] 苏国韶，钱 坤．人工蜂群算法在重力坝断面优化设计中的应用 [J].计算机工程与应用，2011，47(11)：223-225．

Su G S,Qian K.Optimal design of gravity dam section using artificial bee colony algorithm [J].Computer Engineering and Applications,2011,47(11):223-225.

[15] Khatibinia M,Khosravi S.A hybrid approach based on an improved gravitational search algorithm and orthogonal crossover for optimal shape design of concrete gravity dams [J].Applied Soft Computing,2014,16(3):223-233.

[16] 徐云乾，吕爱钟．基于Visual Basic实体重力坝断面优化设计 [J].水电能源科学，2011，29(9)：80-81．

Xu Y Q,Lü A Z.Section optimization design of solid gravity dam based on visual basic [J].Water Resources and Power,2011,29(9):80-81.

[17] 田 艳．基于复形法的混凝土面板堆石坝优化设计研究 [J].水资源与水工程学报，2012，23(2)：160-164．

Tian Y．Research on optimal design of concrete face rockfill dam based on complex method [J].Journal of Water Resources & Water Engineering，2012，23(2)：160-164．

[18] 丁陆军，李守义，刘裕红．基于改进复合形法的拱坝体形优化设计 [J].水电能源科学，2012，30(12)：88-89．

Ding L J,Li S Y,Liu Y H.Shape optimal design of arch dam based on modified complex method [J].Water Resources and Power,2012,30(12)：88-89.

[19] Li S Y,Ding L J,Zhao L J,et al.Optimization design of arch dam shape with modified complex method [J].Advances in Engineering Software,2009,40(9):804-808.

[20] 江沛华，魏 松，汪 莲，等．改进复合形法及其在堆石坝参数反演中的应用 [J].水力发电学报，2011，30(4)：168-174．

Jiang P H,Wei S,Wang L,et al.Modified complex method and application to parameters back-analysis for rock-fill dam [J].Journal of Hydroelectric Engineering,2011,30(4):168-174.

[21] 吕 林，罗 绮，刘俊勇，等．一种基于多种群分层的粒子群优化算法 [J].四川大学学报(工程科学版)，2008，40(5)：171-176．

Lü L,Luo Q,Liu J Y,et al.A Hierarchical structure poly-particle swarm optimization algorithm [J].Journal of Sichuan University(Engineering Science Edition),2008,40(5):171-176.

Optimization of gravity dam section based on double-layer complex method

LI Bin1,YANG Jie1,2

(1InstituteofWaterResourcesandHydro-ElectricEngineering,Xi’anUniversityofTechnology,Xi’an,Shaanxi710048,China；2StateKeyLaboratoryBaseofEco-HydraulicEngineeringinAridArea,Xi’an,Shaanxi710048,China)

【Objective】 Optimization algorithm of gravity dam section design was researched to decrease the cross-section area and optimize the body of gravity dams. 【Method】 Based on the complex method,the contraction steps of searching feasible points under all constraints were simplified for the decrease of calculation times.Then,a double-layer optimization structure was constructed,i.e.the optimization results of the first layer were used as the initial points of the second layer.Complex method was used again for optimization and a gravity dam was optimized as an example.【Result】 All section characteristic parameters met the requirements after optimization,the cross-section area was reduced by 15.97% and the body was thinner.The dam stress distribution of upstream and downstream face were more reasonable.【Conclusion】 Compared with the complex method,double-complex method had higher stability and faster convergence rate,and it can be applied to optimization design of large-volume,complex hydraulic structures.

hydraulic structure;concrete gravity dam;optimization design;double-layer complex method

时间:2016-10-09 10:08

10.13207/j.cnki.jnwafu.2016.11.033

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20161009.1008.066.html

2015-04-30

陕西省重点科技创新团队项目(2013KCT-015)；西北旱区生态水利工程国家重点实验室开放基金项目(106-221210)

李 斌(1989-)，男，陕西西安人，在读硕士，主要从事水工结构与安全监控研究。E-mail：libin_1999@163.com

杨 杰(1971-)，男，四川大邑人，教授，博士生导师，主要从事水工结构、水库大坝安全及除险加固研究。 E-mail：lgdajs@163.com

TV314

A

1671-9387(2016)11-0228-07