非线性Mohr-Coulomb破坏准则下边坡可靠度上限
2016-12-22贺志军曹吉赵炼恒瞿召乾杨胜博
贺志军,曹吉,赵炼恒,瞿召乾,杨胜博
(中南大学 土木工程学院,长沙 410075)

非线性Mohr-Coulomb破坏准则下边坡可靠度上限
贺志军,曹吉,赵炼恒,瞿召乾,杨胜博
(中南大学 土木工程学院,长沙 410075)
传统边坡可靠度分析往往在岩土参数服从线性Mohr-Coulomb(简称线性M-C)破坏准则的假设条件下进行,并且常常采用极限平衡法或有限元法计算安全系数。然而,岩土介质破坏准则具有一定的非线性。为能更加实际地描述岩土破坏机理和得到严格精确的解,基于非线性Mohr-Coulomb(简称非线性M-C)破坏准则,结合极限分析上限法和蒙特卡洛法,进行边坡可靠度上限分析。当非线性参数m=1时,与等效的线性M-C破坏准则进行对比计算,验证了方法的可行性。同时,将初始粘聚力、内摩擦角arctan(c0/σt)和非线性参数作为随机变量且服从截断正态分布,进行了参数变异性和敏感性影响分析。研究表明:非线性M-C破坏准则下,边坡可靠度随初始粘聚力、内摩擦角arctan(c0/σt)和非线性参数变异性的增大而减小;边坡可靠度随初始粘聚力和内摩擦角arctan(c0/σt)的增大而增大,随非线性参数的增大而减小。
边坡;可靠度;破坏准则;极限分析;蒙特卡洛法
边坡稳定性问题一直是岩土工程的一个重要研究内容[1]。目前,边坡稳定性分析主要有两大体系:确定性体系与不确定性体系(可靠度体系)。确定性体系使用极限平衡法、数值模拟法或极限分析法等方法分析边坡的稳定性,求得边坡最小安全系数,以此作为边坡稳定性评价指标。然而,边坡是一个极其复杂的系统,岩土参数具有明显的随机性,采用确定性体系分析边坡稳定性不符实际。文献[2-3]也指出:由于安全系数没有考虑参数随机性和离散型对结果的影响,导致实际工程中很多结构在满足安全系数的条件下依然出现了破坏现象。以概率论为基础的可靠度体系可考虑边坡系统内部的随机关系,可给出边坡稳定程度,因而可以弥补用单一安全系数分析边坡稳定性的局限性。
边坡可靠度分析主要有两大步骤:一是构建计算边坡稳定性安全系数的模型(功能函数);二是使用可靠度分析方法计算边坡可靠度(失效概率或可靠度指标)。在构建模型方面,目前应用最广泛的是极限平衡法,该方法理论简单、易于实施,但所作假设较多,根据塑性理论可知,该方法所获解答不是严格的上下限解。另一应用广泛的方法是数值方法[4-5],该方法将有限元技术应用到边坡稳定性分析中,可以考虑土体与其中结构物的共同作用,但其所得到的极限荷载值仍不够精确。相比上述两种方法,极限分析法可以得到边坡极限荷载的严格上限解,在此基础上进行可靠度分析,可以得到严格边坡可靠度上限值,这对于分析边坡稳定性可能具有重要意义。在可靠度分析方法方面,常用的分析方法有一次二阶矩法[6-7]、JC法[8]、Monte Carlo法[9-10]等。其中,Monte Carlo法被认为是一种相对精确的方法[11],根据大数定律,只要抽样次数足够大,其精度就能足够高。目前,众多学者应用可靠度分析理论对边坡稳定性进行研究均是在线性M-C破坏准则假设下进行的。而事实上,岩土介质服从非线性破坏准则,线性破坏准则只是一种特例:将更为符合实际的略微弯曲岩土材料强度线简化成直线形状,该方法虽简单易于分析,但无法准确表述岩土强度特性。因此,考虑岩土破坏准则为非线性情况下的边坡可靠度研究显得十分必要。1987年,Zhang等[12]提出了幂函数非线性破坏准则,尔后,大量学者[13-18]对基于该破坏准则下的边坡稳定性问题进行了深入研究,非线性M-C破坏准则得到快速发展且已较为成熟。但多年来,鲜见基于非线性M-C破坏准则下边坡可靠度的深入研究。
基于以上考虑,在非线性Mohr-Coulomb破坏准则下,结合外切线技术和强度折减技术计算边坡安全系数上限解,进一步运用蒙特卡洛法计算边坡可靠度。通过与基于线性M-C破坏准则的计算结果进行对比,验证了方法的可行性。并视初始粘聚力c0、内摩擦角arctan(c0/σt)与非线性参数m为随机参数且服从截断正态分布,研究非线性M-C破坏准则下各参数变异性、敏感性对均质各向同性边坡可靠度的影响。
1 非线性M-C破坏准则及抗剪强度参数引入方法
非线性Mohr-Coulomb破坏准则的指数形式简单实用,能较为真实地呈现非线性的Mohr圆包络线,因而被广泛使用,其表达式为
τ=c0·(1+σn/σt)1/m
(1)
式中:τ和σn分别为破坏面上的切向应力和法向应力;c0(≥0)为初始粘聚力;σt(≥0)为单轴拉伸强度;m为控制强度曲线参数(简称非线性参数)。m决定了曲线的弯曲程度,当m=1时,式(1)变为线性M-C破坏准则

(2)
式中:c0等同于线性M-C强度理论中的粘聚力c(c0=c);c0/σt等同于线性M-C强度线中的斜率tanφ(c0/σt=tanφ)。
将式(1)绘成曲线,如图1所示。

图1 非线性M-C破坏准则示意图Fig. 1 Diagram of nonlinear M-
结构上限分析时,提高材料的屈服强度不会降低结构的极限荷载。因而对非线性破坏准则下的边坡上限分析可采用“外切线法”[12],以提高岩土材料强度为手段来分析结构物的上限解。图1中,在破坏面上某切点G处作切线,以此切线来确定岩土非线性强度参数。切线方程为
τ=ct+tan φt·σn
(3)
式中:ct和tan φt分别表示切线的截距和斜率,其表达式为
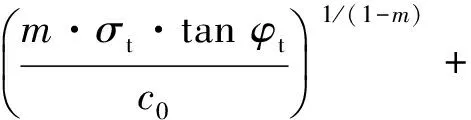
σt·tan φt
(4)

(5)
2 基于强度折减技术的边坡极限分析上限法
边坡可靠度分析中,安全系数计算式表示了边坡安全系数与土工参数之间的关联关系,作为功能函数的构建主体至关重要。极限分析上限法基于虚功率原理推导,根据外力做功和内部耗能相等原理获得目标函数并根据能量耗散最小化原理获得极限荷载的最小值,进一步结合强度折减技术可获得严格精确的安全系数上限解。

图2 对数螺旋面破坏机构Fig.
选取符合简单边坡的对数螺旋面破坏机构作为破坏模式[19-20],以通过坡趾下的对数螺旋线旋转间断机构为例进行分析,如图2。刚性块体ABC′CA绕旋转中心O相对对数螺旋面BC′以下的静止材料作刚体旋转,BC′是速度间断面。ABC′CA区重力做功率为外荷载功率;间断面BC′上滑面耗损率为内能耗散率。根据上限法能耗计算过程,使外荷载功率等于内能耗散率,可求得边坡的临界高度Hcr。结合外切线技术,通过引入强度折减技术[21],原始非线性抗剪强度指标变为
(6)
令折减后的边坡临界自稳高度等于原始高度(Hcr=H),可得边坡安全系数表达式
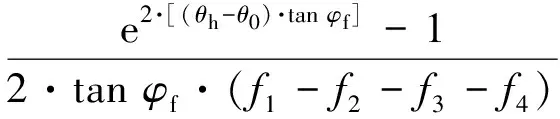
(7)
式中:θ0、θh、β′和r0为几何变量,详见图2;γ为岩土容重;H为边坡高度;f1、f2、f3和f4分别为OBC′O、OABO、OAC′O、ACC′A区土重所做功率相关参数,详见文献[14],不再赘述。
在已知边坡几何尺寸及岩土材料参数条件下,边坡安全系数Fs可由θh、θ0、β′、φt等4个未知参数确定,且安全系数计算公式是Fs的隐函数。将Fs作为目标函数,通过非线性数学规划方法,利用Matlab软件,可求得边坡最小安全系数Fs。
3 基于非线性M-C破坏准则的边坡可靠度上限计算
3.1 岩土随机参数的选定及其分布类型
线性M-C破坏准则下岩土参数分布类型已有大量研究成果。马建全等[22]认为不同环境下岩土参数具有不用分布类型,同时,比较了岩土参数服从正态分布、对数正态分布等不同分布类型下的边坡可靠度大小;张继周等[23]从概率分布类型的产生背景、所描述对象的物理意义入手,研究各分布类型对可靠度分析的影响,得出正态分布和对数正态分布较为合理的结论;其他众多边坡可靠度研究[24-27]亦在岩土参数服从正态分布下进行。因此,笔者也选取正态分布作为岩土随机参数的分布类型。
线性M-C破坏准则下,岩土参数c与φ服从正态分布。由式(2)可知,当m=1时,非线性M-C破坏准则指数型表达式中的参数c0与无量纲参数c0/σt的反正切值arctan(c0/σt)服从正态分布。当m≠1时,假设参数c0与内摩擦角arctan(c0/σt)服从正态分布,并进一步考虑非线性参数的变异性,假设m亦服从正态分布。由此,选取初始粘聚力c0、内摩擦角arctan(c0/σt)与非线性参数m作为随机参数。
桂勇等[24]在边坡稳定二元体系的建立中,采用同时考虑材料指标的统计分布和区间分布的方法,即截断分布;Johari等[25]在基于毕绍普法的地震边坡稳定概率模型建立中,采用截断正态分布作为随机变量的概率分布。截断分布可以考虑岩土参数具体变化范围,更符合工程实际。选取截断的正态分布作为岩土随机参数的分布类型,随机参数概率密度函数为
(c0)min≤c0≤(c0)max
(8)
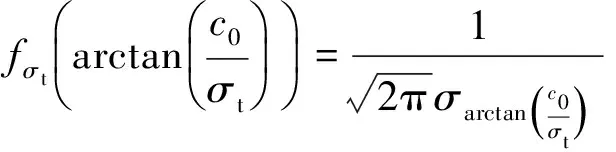

(9)
mmin≤m≤mmax
(10)
式中:
(11)
由式(11)可知,随机参数落在该范围内的概率达99.994%。实际工程中,岩土材料参数不会出现负值;非线性参数m取值范围为1~2[28]。因此,随机参数还需满足条件
(12)
3.2 边坡可靠度上限计算
非线性M-C破坏准则下,边坡安全系数上限解Fs如式(7),则相应的功能函数为
Z=Fs-1
(13)
相应的工作状态可表示为
(14)
失效概率与可靠指标分别表示为
pf=P{G(X)<0}=P{Fs<1}=∫Dff(X)dX
(15)
β=Φ-1(1-pf)
(16)
式中:X={x1,x2,…,xn}T是具有N维随机变量的向量;f(X)=f(x1,x2,…,xn)是基本随机变量X的联合概率密度函数;G(X)是结构的极限状态函数;Df是与G(X)相对应的失效区域;Φ-1(·)为标准正态分布函数的反函数。
与其他可靠度计算方法相比,Monte Carlo模拟法具有不受分析条件限制、计算精度高等优点,得到广泛应用。采用蒙特卡洛法直接计算非线性破坏准则下边坡可靠度上限值。
1)根据各随机参数的分布,对c0、arctan(c0/σt)和m产生N组样本,分别为{(c0)1,(c0)2,…,(c0)N}、{(arctan(c0/σt))1,(arctan(c0/σt))2,…,(arctan(c0/σt))N}和{m1,m2,…,mN}。
2)计算参数σt
(n=1,2,3,...,N)
(17)
3)以(c0)n、(σt)n和mn作为岩土材料参数,由式(4)与式(5)解得非线性抗剪指标(ct)n与(φt)n,由式(6)与式(7)求得安全系数上限值(Fs)n。
4)重复步骤3),得到N个安全系数{(Fs)1,(Fs)2,…,(Fs)N},统计其小于1的数量为M个。
5)根据蒙特卡洛原理,得到失效概率为
(18)
可靠指标可由式(16)求解。工程中,为满足一定的精度,得到可靠估计,抽样数目N须满足
(19)
4 对比分析
目前,鲜有非线性M-C破坏准则方面的边坡可靠度研究。为验证方法的可行性,基于线性M-C破坏准则将边坡可靠度上限解与Johari等[25]、蔡宁等[26]及吕杨[27]的计算结果进行对比分析。参数信息如表1所示,对比结果如表2所示。
表1 参数信息
Table 1 Parameters information

来源随机参数固定参数Johari等[25]μc=10.0kPa,σc=2.0kPa;μφ=28.0°,σφ=2.8°;μγ=18.0kN/m3,σγ=0.9kN/m3。H=12.0m,β=45°。服从正态分布蔡宁等[26]μc=10kPa,σc=1.5kPa;μφ=10°,σφ=1.5°。γ=17.64kN/m3,H=5m,β=26.6°。服从正态分布吕杨[27]μc=10kPa,σc=3kPa;μφ=21.72°,σφ=6.516°;μγ=20kN/m3,σγ=1.2kN/m3。H=8m,β=33.7°。服从正态分布
表2 不同安全系数计算方法下边坡可靠度对比
Table 2 Comparisons of the slope reliability with different safey factors calculation method

来源安全系数计算方法其他文献Pf/%β本文Pf/%增大/%β减小/%Johari等[25]Bishop16.430.97716.862.620.95971.77蔡宁等[26]Morgenstern⁃price0.752.4320.795.332.41350.76吕杨[27]Bishop14.421.07014.550.901.05591.32吕杨[27]M⁃P14.411.06214.550.971.05590.57
由表2可知,线性M-C破坏准则下本文结算结果与Johari等[25]、蔡宁等[26]及吕杨[27]的计算结果失效概率Pf最大相差5.33%。最小相差0.90%,平均相差2.455%;可靠指标β最大相差1.77%,最小相差0.57%,平均相差1.105%,表明该方法可行。
5 算例分析
选取一典型边坡作为研究对象,如图3所示。研究依据文献[12]确定岩土材料参数c0和σt,获得参数c0与内摩擦角arctan(c0/σt)的均值,分别为90 kN/m2与20°(σt为247.3 kN/m2)。并假设坡角α=60°,坡高H=25 m,岩土容重γ=20 kN/m3,非线性参数均值μm=1.6。随机参数变异系数取值情况为:1)参数c0与内摩擦角arctan(c0/σt)沿用Johari等[25]的c与φ的变异系数,分别为0.20与0.10。2)非线性参数m对于不同岩土材料有一定变化范围[29-32],因此,非线性参数m取较小变异系数符合实际工程,取值为0.05。截断的正态分布随机参数如表3所示。
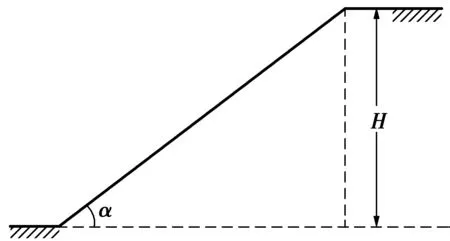
图3 典型边坡Fig. A typical slope
Table 3 Stochastic parameters with truncated normal distribution

随机参数均值标准差最小值最大值c0/(kN·m-2)900.20c018162arctan(c0/σt)200.10×arctan(c0/σt)1228m1.60.05m1.281.92
5.1 参数变异性影响
为分析非线性M-C破坏准则下随机参数(以下简称参数)的变异性对边坡可靠度的影响,进行参数变异性影响分析。当参数变异系数的增加值δ=0、COV/3、2COV/3、3COV/3、4COV/3、5COV/3、6COV/3时,边坡失效概率Pf的变化情况如图4所示;边坡可靠指标β的变化情况如图5所示。对应(δ=0、δ=COV)的安全系数统计结果对比如图6~7所示;对应(δ=0、δ=COV)的可靠度相对变化如表4所示。
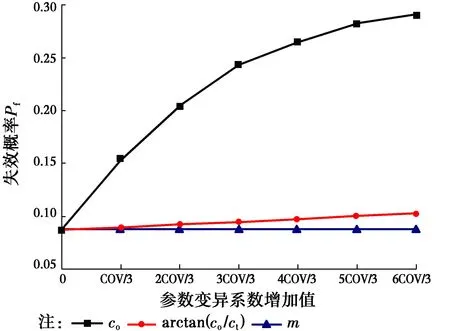
图4 失效概率Pf随参数变异系数的变化情况Fig.4 probability of failure Pf with respect to change of variation coefficients of parameters

图5 可靠指标β随参数变异系数的变化情况Fig.5 Variation of reliability index β with respect to change of variation coefficients of parameters
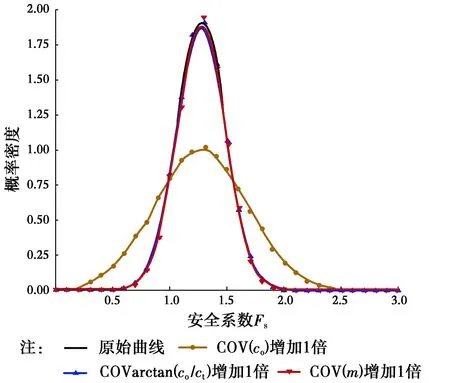
图6 不同变异系数下安全系数Fs的概率密度分布Fig.6 Probability density distribution of safety factor Fs for different variation coefficients

图7 不同变异系数下安全系数Fs的累积概率密度分布Fig.7 Cumulative density distribution of safety
Table 4 Relative change of reliability for double variation coefficient

随机参数初始粘聚力c0内摩擦角arctan(c0/σt)非线性参数m失效概率Pf0.24340.09430.0874变化/%+178.81+8.02+0.11可靠指标β0.69541.31471.3569变化/%-48.78-3.16-0.05
由图4~7与表4可知,初始粘聚力c0的变异性对边坡可靠度具有较大影响;内摩擦角arctan(c0/σt)与非线性参数m的变异性对边坡可靠度的影响较小。随着初始粘聚力变异系数的增大,边可靠度减小得较为明显,且这种变化幅度随着变异系数的增大逐渐减小;随着内摩擦角arctan(c0/σt)与非线性参数变异系数的增大,边坡可靠度减小且较为缓慢。
对于该算例,岩土材料参照文献[12]选取,其初始粘聚力为90 kN/m2,初始内摩擦角arctan(c0/σt)为20°。已有研究表明[14],结合上限理论与外切线技术后,所获得的瞬时粘聚力ct随非线性参数的增大而增大,而瞬时内摩擦角φt随非线性参数的增大而减小,可知该算例中粘聚力参数对边坡稳定性的影响占主导作用。同时,加之在计算过程中选取了较大的变异系数(20%),使得初始粘聚力的变异性对边坡可靠度影响较其它参数大得多。
5.2 敏感性分析
为研究在非线性M-C破坏准则下随机参数(以下简称参数)的变化对边坡可靠度的影响,进行参数敏感性分析。当参数均值的增加值δ=0、std/3、2std/3、3std/3、4std/3、5std/3、6std/3时,边坡失效概率Pf的变化情况如图8所示;边坡可靠指标β的变化情况如图9所示。对应(δ=0、δ=std)的安全系数统计结果对比如图10~11所示;对应(δ=0、δ=std)的可靠度相对变化如表5所示。

图8 失效概率Pf随参数均值的变化情况Fig.8 probability of failure Pf with respect to change of mean values of paramters

图9 可靠指标β随参数均值的变化情况Fig.9 reliability index β with respect to change of mean values of paramters

图10 不同参数均值下安全系数Fs概率密度分布Fig.10 Probability density distribution of safety

图11 不同参数均值下安全系数Fs累积概率密度分布Fig.11 Cumulative density distribution of safety factor
Table 5 Relative change of reliability for mean values of parameters plus 1std

随机参数失效概率Pf失效概率变化/%可靠指标β可靠指标变化/%初始粘聚力c00.0272-68.841.9236+41.69内摩擦角arctan(c0/σt)0.0731-16.271.4531+7.03非线性参数m0.1049+20.161.2541-7.62
由图8~11和表5可知,初始粘聚力c0的均值对边坡可靠度有较大影响;无量纲参数arctan(c0/σt)与非线性参数m的均值对边坡可靠度的影响相对较小。随着初始粘聚力和无量纲参数arctan(c0/σt)均值的增大,抗剪强度参数ct和φt均增大,边坡可靠度增大;随着非线性参数均值的增大,抗剪强度参数ct和φt发生变化,边坡可靠度减小。
6 结论
基于非线性M-C破坏准则,结合外切线技术和强度折减技术,采用极限分析上限法求得边坡安全系数上限解,进一步运用蒙特卡洛法计算边坡的可靠度(失效概率Pf与可靠指标β)。在线性M-C破坏准则下,通过与已有算例对比计算,验证了方法的可行性。同时,基于非线性破坏准则分析参数变异性和参数敏感性对边坡可靠度的影响,得到如下结论:
1)边坡可靠度随初始粘聚力c0、内摩擦角arctan(c0/σt)和非线性参数m变异系数的增大而减小。
2)边坡可靠度随初始粘聚力c0和内摩擦角arctan(c0/σt)均值的增大而增大,随非线性参数m均值的增大而减小。
工程实际中,岩土材料参数分布形态众多,笔者研究的基于非线性M-C破坏准则的边坡可靠度上限分析仅采用截断正态分布这一种,其他分布形态的研究有待深入;岩土材料参数取值范围和变异系数差异较大,研究的基于非线性M-C破坏准则的边坡可靠度上限分析采用了已有文献中参数分析的取值,符合工程实际的其他参数取值范围和变异性的研究有待深入。
[1] 夏元友, 李梅. 边坡稳定性评价方法研究及发展趋势[J]. 岩石力学与工程学报, 2002, 21(7): 1087-1091. XIA Y Y, LI M. Evaluation method research of slope stability and its developing trend [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(7): 1087-1091. (in Chinese)
[2] JIMENEZ-RODRIGUEZ R, SITAR N, CHACON J. System reliability approach to rock slope stability [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 847-859.
[3] JIMENEZ-RODRIGUEZ R, SITAR N. Rock wedge stability analysis using system reliability methods [J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 419-427.
[4] FARAH K, LTIFI M, HASSIS H. Reliability analysis of slope stability using stochastic finite element method [J]. Procedia Engineering, 2011, 10: 1402-1407.
[5] 谭晓慧, 王建国, 刘新荣, 等. 边坡稳定的有限元可靠度计算及敏感性分析[J]. 岩石力学与工程学报, 2007, 26(1): 115-122. TAN X H, WANG J G, LIU X R, et al. Finite element reliability computation and sensitivity analysis of slope stability [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 115-122. (in Chinese)
[6] ZHANG J, ZHANG L M, TANG W H. New methods for system reliability analysis of soil slopes [J]. Canadian Geotechnical Journal, 2011, 48(7): 1138-1148.
[7] EL-RAMLY H, MORGENSTERN N R, CRUDEN D M. Probabilistic slope stability analysis for practice [J]. Canadian Geotechnical Journal, 2002, 39(3): 665-683.
[8] 赵国藩. 工程结构可靠性理论与应用[M]. 辽宁 大连: 大连理工大学出版社, 1996.
[9] AU S K, CAO Z J, WANG Y. Implementing advanced Monte Carlo simulation under spreadsheet environment [J]. Structural Safety, 2010, 32(5): 281-292.
[10] WANG Y, CAO Z, AU S K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet [J]. Canadian Geotechnical Journal, 2010, 48(1): 162-172.
[11] ZHANG H, DAI H, BEER M, et al. Structural reliability analysis on the basis of small samples: an interval quasi-Monte Carlo method [J]. Mechanical Systems and Signal Processing, 2013, 37(1): 137-151.
[12] ZHANG X J, CHEN W F. Stability analysis of slopes with general nonlinear failure criterion [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33-50.
[13] 赵炼恒, 李亮, 但汉成, 等. 极限上限分析中“切线法”引入非线性破坏准则的探讨[J]. 长江科学院院报, 2010, 27(8): 34-39. ZHAO L H, LI L, DAN H C, et al. Discussion on generalized tangential method led in nonlinear failure criterion in upper boundary limit analysis [J]. Journal of Yangtze River Scientific Research Institute, 2010, 27(8): 34-39. (in Chinese)
[14] ZHAO L, LI L, YANG F, et al. Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique [J]. Journal of Central South University of Technology, 2010, 17: 836-844.
[15] ZHAO L, YANG F, ZHANG Y, et al. Effects of shear strength reduction strategies on safety factor of homogeneous slope based on a general nonlinear failure criterion [J]. Computers and Geotechnics, 2015, 63: 215-228.
[16] 张迎宾, 李亮, 赵炼恒, 等. 基于非线性破坏准则的边坡稳定性极限分析[J]. 岩土力学, 2011, 32(11): 3313-3318. ZHANG Y B, LI L, ZHAO L H, et al. Limit analysis of slope stability based on nonlinear failure criterion [J]. Rock and Soil Mechanics, 2011, 32(11): 3313-3318. (in Chinese)
[17] YANG X, CHI S. Upper bound finite element analysis of slope stability using a nonlinear failure criterion [J]. Computers and Geotechnics, 2013, 54: 185-191.
[18] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.
[19] CHEN W F. Limit analysis and soil plasticity [M]. Amsterdam: Elsevier ASCE, 1975.
[20] DAWSON E M, ROTH W H, DRESCHER A. Slope stability analysis by strength reduction [J]. Geotechnique, 1999, 49(6): 835-840.
[21] DUNCAN J M. State of the art: limit equilibrium and finite-element analysis of slopes [J]. Journal of Geotechnical engineering, 1996, 122(7): 577-596.
[22] 马建全, 李广杰, 张文, 等. 基于可靠度的边坡稳定性影响因素[J]. 吉林大学学报 (地球科学版), 2011, 41(Sup1): 187-194. MA J Q, LI G J, ZHANG W, et al. Influence factors analysis of slope stability based on reliability[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(Sup1): 187-194. (in Chinese)
[23] 张继周, 缪林昌. 岩土参数概率分布类型及其选择标准[J]. 岩石力学与工程学报, 2009, 28(Sup2): 3526-3532. ZHANG J Z, MIU L C. Types and selection criteria of probability distribution of rock and soil parameters [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Sup2): 3526-3532. (in Chinese)
[24] 桂勇, 邓通发, 罗嗣海, 等. 基于蒙特卡罗边坡稳定二元体系的建立与应用[J]. 岩土力学, 2014, 35(7): 1979-1986. GUI Y, DENG T F, LUO S H, et al. Establishment of slope stability dual index system based on Monte Carlo simulation and its application [J]. Rock and Soil Mechanics, 2014, 35(7): 1979-1986. (in Chinese)
[25] JOHARI A, MOUSAVI S, NEJAD A H. A seismic slope stability probabilistic model based on Bishop's method using analytical approach [J]. Scientia Iranica, Transaction A, Civil Engineering, 2015, 22(3): 728.
[26] 蔡宁, 赵明华. 边坡稳定可靠度替代模型分析[J]. 中南大学学报: 自然科学版, 2014, 45(8): 2851-2856. CAI N, ZHAO M H. Analysis of alternative model for slope stability reliability [J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2851-2856. (in Chinese)
[27] 吕杨. 土质路堤边坡稳定可靠度分析方法探讨[D]. 成都: 西南交通大学, 2014. LYU Y. Discussion on the method of stability reliability of embankment slope [D]. Chengdu: Southwest Jiaotong University, 2014. (in Chinese)
[28] JIANG J C, BAKER R, YAMAGAMI T. The effect of strength envelope nonlinearity on slope stability computations [J]. Canadian Geotechnical Journal, 2003, 40(2): 308-325.
[29] 刘宝琛, 崔志莲, 涂继飞. 幂函数型岩石强度准则研究[J]. 岩石力学与工程学报, 1997, 16(5): 437-444. LIU B C, CUI Z L, TU J F. A study of strength criterion in power function for rock material [J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(5): 437-444. (in Chinese)
[30] JIANG J C, BAKER R, YAMAGAMI T. The effect of strength envelope nonlinearity on slope stability computations [J]. Canadian Geotechnical Journal, 2003, 40(2): 308-325.
[31] CHARLES J A, SOARES M M. The stability of slopes in soils with nonlinear failure envelopes [J]. Canadian Geotechnical Journal, 1984, 21(3): 397-406.
[32] LI D, CHENG Y. Lower bound limit analysis using nonlinear failure criteria [J]. Procedia Earth and Planetary Science, 2012, 5: 170-174.
(编辑 胡英奎)
Upper bound reliability analysis of slope with nonlinear Mohr-Coulomb failure criterion
HeZhijun,CaoJi,ZhaoLianheng,QuZhaoqian,YangShengbo
(School of Civil Engineering, Central South University, Changsha 410075, P. R. China)
Traditional reliability analysis of slope is often performed under linear Mohr-Coulomb (M-C) failure criterion assumption and using limit equilibrium method or finite element method which is for calculating the safety factor. However, the failure criterion of geomaterials is nonlinear. In this paper, upper bound reliability analysis of slope is performed using upper bound limit analysis and Monte Carlo simulation based on nonlinear Mohr-Coulomb failure criterion, which is for a more practical description of the failure mechansim of geomaterials and obtaining strictly accurate answers. When the nonlinear parametermis equal to one, the expressions in this study convert into linear Mohr-Coulomb failure criterion, and thus the feasibility of this study is verified by comparing with other results. Meanwhile, initial cohesion, internal friction angle arctan(c0/σt) and nonlinear parameter are selected as the stochastic parameters which are considered to have a truncated normal distribution, and the effects of variability and sensitivity of parameters are analysed. The results show that reliability of slope decreases with the variability of initial cohesion, internal friction angle arctan(c0/σt) and nonlinear parameter; reliability of slope increases with initial cohesion and internal friction angle arctan(c0/σt), and decreases with nonlinear parameter.
slope; reliability; failure criterion; limit analysis; Monte Carlo simulation
2016-03-04
国家自然科学基金(51208522、51478477);贵州省交通运输厅科技项目(2012122033、2014122006)
贺志军(1965- ),男,博士,研究员,主要从事交通运输工程研究,(E-mail)13807316922@139.com。 赵炼恒(通信作者),男,博士后,副教授,博士生导师,(E-mail)zlh8076@163.com。
Foundation item:National Natural Science Foundation of China (No. 51208522, 51478477); Guizhou Provincial Department of Transportation Foundation(No. 2012122033, 2014122006)
10.11835/j.issn.1674-4764.2016.06.001
TU 457
A
1674-4764(2016)06-0001-09
Received:2016-03-04
Author brief:He Zhijun (1965- ), PhD, research fellow, main research interest:traffic & transportation engineering,(E-mail) 13807316922@139.com. Zhao Lianheng (corresponding author), post-doctoral, associate professor, doctoral supervisor, (E-mail)zlh8076@163.com.
