基于SOLO分类理论的高考数学试题评价研究——知识点考查的视角*
2016-12-21曾建国
曾建国
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
·教学理论研究·
基于SOLO分类理论的高考数学试题评价研究
——知识点考查的视角*
曾建国
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
SOLO分类理论应用于高考试题评价研究一般是先编制相关学科试题的SOLO水平层次划分标准,然后据此对各道试题进行分析,判断其属于某一SOLO水平层次.但这种试题评价结果对高中数学教学缺乏指导意义.本文应用SOLO分类理论,从知识点考查的视角来评价高考数学试题.并以三角函数模块为例进行评价分析,试图了解高考试题对相关知识点考查的力度.
SOLO分类理论;高考数学试题;知识点考查
1 引言
自比格斯(John B.Biggs)20世纪末提出SOLO分类理论[1]至今,其应用研究取得了众多成果.21世纪初期SOLO分类理论的应用研究主要集中于各学科开放性试题的评分应用以及教学中用于评价检测[2],随后有人应用于试题难度预估[3].近年来有人也将SOLO分类理论应用于中高考试题评价研究[4-9],我们发现,此类研究主要集中在文科试题以及物理、化学等理科试题的评价,而应用于高考数学试题评价的研究成果很少.本文拟在这方面作一点尝试,从知识点考查的视角,应用SOLO分类理论,对高考数学试题进行评价研究.
2 “试题的SOLO层次评价法”存在的缺陷
由于SOLO分类评价法是一种以等级描述为基本特征的质性评价方法,因此,SOLO分类理论应用于数学试题(特别是数学高考试题)评价研究的成果非常少见,多见于文科试题及开放性特征较明显的理科试题评价研究.此类研究一般先根据SOLO分类理论编制相关学科试题的SOLO水平层次划分标准,然后依据这个划分标准依次对每一道试题分析,评判其属于哪一个SOLO层次(不妨称之为“试题的SOLO层次评价法”),并进行统计、比较和分析[4-9].通过分析相关试题评价研究成果发现,这种试题的SOLO层次评价法普遍应用于文科类试题的评价研究,但是不可否认,试题的SOLO层次评价法存在一些缺陷,如果在高考数学试题评价中应用此评价法,这些缺陷会更加明显.
2.1 其他学科的SOLO层次划分方法不太适合高考数学试题
文科试题与数学试题差异较大,故此我们选择理科试题评价的若干文献进行分析.
文献[4]和文献[5-6]分别编制的物理和化学高考试题评价的SOLO层次划分方法基本相近,如表1所示:

表1 高考物理试题SOLO层次划分[4]

表2 高考化学试题SOLO层次划分[5](文献[6]也与此表基本相近)
即使对于物理、化学这样的理科高考试题所编制的上述SOLO层次划分方法,也不太适合对于数学试题的评价.这是因为,与物理化学试题不同,数学试题的难易程度并非仅仅由题目所涉及的信息量、知识点多少而定,而更能影响数学试题难度的是其思维难度,比如一道信息量和涉及知识点很少的数学试题完全可能具有较高难度.因此对数学试题评价时“不应该按照知识点来划分SOLO水平”[7].
文献[7~8]考虑到按知识点来划分数学试题SOLO水平层次不够合理的弊端,直接按照比格斯(John B.Biggs)的SOLO水平层次划分来评价中考数学试题,而没有另外制定具体的针对数学试题的SOLO水平层次划分方法.这样虽然便于灵活处理,但对试题的评价难免受主观因素影响较大,评价标准不够明晰势必影响评价结果的真实性和可靠性.哪怕同一道试题,两个人来评价都可能出现完全不同的结果.研究者已认识到SOLO评价理论的这一局限性:“……不同的教师对层次的理解和划分会不可避免地带有个人的主观色彩而有差异”“……如何划分不同的层次结构水平,是教师运用此评价法遇到的难题之一”.[10]
另外,此类研究一般都是采用试题的SOLO层次评价法,笔者认为这种试题评价显得比较笼统.例如,某一道试题有几个小题,有的小题可能为单一结构,而其他小题则应划分为关联结构甚至拓展抽象结构,最终只能评价此题归为某一个层次,现有此类研究大都如此[4-9],这样的评价难免失真.
总之,现有的试题评价研究中SOLO层次划分方法大多不太适合于高考数学试题的评价.
2.2 “试题的SOLO层次评价法”得到的评价结果对高考复习教学缺乏指导意义
即便我们也按照试题的SOLO层次评价法,对每一道高考数学试题进行分析,逐一评判其属于哪一个SOLO层次,并进行统计、比较和分析.这样的试题评价对高中数学教学及高考复习应考意义也不大.试想,即使我们对一套高考数学试题评价研究得出结论:此套试题单一结构、多元结构、关联结构、拓展抽象结构的试题各占多少比例;再对若干套试题进行比较,得出其差异、变化趋势……我们仍想象不出这些评价结果对于高中数学教学及高考复习有何指导意义.
为了改变如上所述试题的SOLO评价法不太适合高考数学试题评价研究,且这种评价对教学指导意义不大的状况,我们不妨转换研究思路,尝试从知识点考查的视角来评价高考数学试题.
3 高考数学试题“知识点考查的SOLO层次评价法”
教师关注数学高考题,除了高考题的题型、结构、难度等方面,更多关心的是试题对各知识点考查的力度.即教师更关注高考数学试题对各知识点考查时孰重孰轻.了解了这些信息,才有利于教师把握高中数学教学与高考复习的方向.
本文尝试不单独评价每一道试题的SOLO水平层次,转而评价一份试卷对某个知识点的考查属于哪一个SOLO水平层次(不妨称这种评价方式为“知识点考查的SOLO层次评价法”),进而综合比较可以得出某一模块(乃至整个)高考数学内容的各知识点在这份试卷中考查的力度.为此,我们参照已有的各种针对试题编制SOLO层次划分方法,编制高考数学“知识点考查的SOLO层次”划分方法如下:

表3 高考数学知识点考查的SOLO层次划分
下面举例说明这种知识点考查的SOLO层次评价法在试题评价中的具体应用:
例1 (2013年上海春季高考理)既是偶函数又在区间(0,π)上单调递减的函数是( ) (答案 B)
(A)y=sinx(B)y=cosx(C)y=sin 2x(D)y=cos 2x
此题考查三角函数的两个知识点:奇偶性、单调性.判断奇偶性只涉及单一的函数,只需了解奇偶函数定义就可判断(B)、(D)两个函数是偶函数,根据表3可知,对三角函数奇偶性的考查属于单一结构水平(U);判断函数(B)y=cosx在区间(0,π)上单调递减也属于单一结构水平(U),因为只需要了解余弦函数的性质就能得出结论.



同样也考查三角函数的单调性,此题却涉及三角变换、三角函数的值域、二次函数的单调性、复合函数等多个知识点,且必须有机地联系起来,对照表3可以得出此题对于三角函数单调性考查属于关联结构水平(R),而对于三角变换、值域、二次函数的单调性、复合函数等知识点的考查均属于单一结构水平(U).
4 “知识点考查的SOLO层次评价法”的应用(以三角函数模块为例)
本文以2011-2015年高考全国卷I理科三角函数模块为例,说明这种知识点考查的SOLO层次评价法在高考数学试题评价中的应用.
4.1 全国卷I理科三角函数模块知识点考查SOLO水平统计
根据表3,对2011-2015年高考全国卷I理科三角函数模块各知识点考查的SOLO水平情况统计如下(知识点分布参照数学高考考试说明):

表4 2011年全国卷I理科三角函数知识点考查SOLO水平统计表

表5 2012年全国卷I理科三角函数知识点考查SOLO水平统计表

表6 2013年全国卷I理科三角函数知识点考查SOLO水平统计表

表7 2014年全国卷I理科三角函数知识点考查SOLO水平统计表

表8 2015年全国卷I理科三角函数知识点考查SOLO水平统计表
几点说明:
(1)特殊角的三角函数值归为知识点“三角函数定义”;
(2)正弦定理的应用中,若涉及边角转换,关联到正弦定理及对式子的特点的判断(是否为齐次、变换方向的选择)等方面,因此归为关联结构(R)层次.如2014年16题:将等式(2+b)(sin A-sin B)=(c-b)sin C变形为(2+b)(a-b)=(c-b)c过程对正弦定理考查的SOLO水平属于关联结构(R)层次.
4.2 全国卷I理科三角函数模块知识点考查情况分析
根据2011-2015年高考全国卷I理科试题对三角函数模块各知识点考查的SOLO水平统计我们发现:
4.2.1 三角函数试题难度不大,大都属于中低档难度,试题对该模块知识点考查覆盖面广
将表1-5中三角函数知识点考查的SOLO水平各等级次数统计后发现(见图1),2011-2015年全国卷I理科高考试题对三角函数各知识点考查的SOLO水平最高等级只有关联结构水平(R),表明三角函数在高考命题以中、低档难度的试题为主,未出现难题.而近5年的试题覆盖了几乎所有知识点(见图2),三角函数定义、图像和性质、三角变换及解三角形等知识点均有试题涉及.
4.2.2 重点考查三角函数基础知识、基本技能

图1 2011-2015年全国卷I理科高考题三角函数知识点考查SOLO水平层次分布
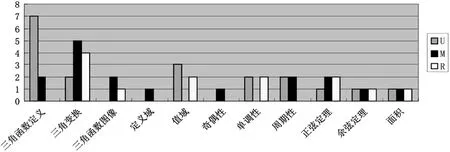
图2 2011-2015年全国卷I理科高考题三角函数知识点考查情况
数学高考考试说明中的命题指导思想明确指出:“命题注重考查考生的数学基础知识、基本技能和数学思想方法”.从图2可以看出,近5年全国卷I理科高考三角函数试题对三角函数模块考查次数最多、力度最大的是“三角函数定义”“三角变换”(图2中相对较高的关联结构水平考查最多之处是“三角变换”),这正体现了注重考查基础知识、基本技能的高考命题指导思想.
通过以上分析,我们在三角函数部分的教学及复习中,应让学生全面学习三角函数的概念、图像和性质,掌握解三角形的知识和方法,做到不留死角,注重基础知识的教学,强化基本技能的训练,对于该部分内容的练习和测试不宜拔高要求,应以中低档难度练习题为主.
5 结语
与以往有关试题评价研究采用逐一评价各试题的SOLO层次的方法不同,本文采用了“知识点考查的SOLO层次评价法”在数学高考试题评价研究方面进行了一点尝试,力求SOLO分类理论应用于试题评价研究的方式方法有所改进.受篇幅所限,本文仅分析评价了全国卷I三角函数模块的高考试题,其他模块内容及其他高考试题有待进一步研究.
[1] John B.Biggs, Kevin F.Collis. 学习质量评价:SOLO分类理论[M].高凌飚,张洪岩,译.北京:人民教育出版社,2010.
[2] 冯翠典,高凌飚.现状与反思:SOLO分类法国内应用研究十年[J].理论与技术,2009,(11):4-7.
[3] 朱行建.SOLO 评价:一种试题难度预估的新方法[J].教学与管理,2010,(9):76-77.
[4] 山丽娟.高考物理试卷能力结构研究——将SOLO理论运用于试题内容分析初探[D].上海:华东师范大学,2011.
[5] 陈莉靖.福建省自主命题下高考化学试题能力结构研究——基于SOLO分类理论[D].福州:福建师范大学,2013.
[6] 吴佳丹.新课程背景下高考化学试题能力导向研究——基于SOLO分类法的试题能力结构分析[D].武汉:华中师范大学,2012.
[7] 宛宝立.用SOLO分类评价理论评价吉林中考试卷[D].长春:东北师范大学,2012.
[8] 胡秀丽.用SOLO分类评价理论评价数学中考试卷——以2013年广东省数学中考试卷为例[J].中学数学研究,2013,18:21.
[9] 陈开懋.新课程背景下高考数学试题能力导向研究——基于SOLO分类理论的试题能力结构分析[J].数学教学通讯,2013,(27):2-3.
[10] 李春玉.SOLO分类评价法在学生学业评价中的优势与局限[J].教学与管理,2013,(10):65-67.
Researches on Evaluation of the Test Questions in Matriculation Mathematics Test Based on the SOLO Taxonomy Theory——A Perspective of Knowledge Point Examining
ZENG Jianguo
(SchoolofMathematicsandComputerScience,GannanNormalUniversity,Ganzhou341000,China)
SOLO taxonomy theory applied to the evaluation of test questions in matriculation mathematics test is generally to divide SOLO level into different levels according to related standard, and then use it to analyze the test questions, decide which SOLO level the question belongs to. But these kind of results lack of guidance to the high school teaching. In this paper, we use the SOLO taxonomy theory to evaluate the test questions of matriculation mathematics from a perspective of knowledge point examining.We take trigonometric functions module as an example to evaluate and analyze, trying to understand the knowledge point examined related to the test questions in matriculation mathematics test.
the SOLO Taxonomy Theory; test questions in Matriculation Mathematics Test ; knowledge point examining
2016-10-09
10.13698/j.cnki.cn36-1346/c.2016.06.031
江西省教育科学“十二五”规划课题(14YB080)
曾建国(1965-),男,江西于都人,赣南师范大学数学与计算机科学学院教授,研究方向:数学教育及距离几何.
http://www.cnki.net/kcms/detail/36.1037.C.20161209.1521.062.html
G633.51
A
1004-8332(2016)06-0130-05
