煤堆场静态扬尘规范计算公式误差分析与修正

杨涛，刘良志，朱平

（1.天津大学建筑工程学院，天津 300072；2.天津北洋水运水利勘察设计研究院，天津 300450）

煤堆场静态扬尘规范计算公式误差分析与修正

杨涛1，刘良志2，朱平2

（1.天津大学建筑工程学院，天津 300072；2.天津北洋水运水利勘察设计研究院，天津 300450）

文中对JTS 105-1—2011《港口建设项目环境影响评价规范》中的煤堆场起尘量计算公式进行了分析，针对使用中存在的一些问题提出改进意见，特别是结合AR模型（Auto-Regressive）采用MATLAB定量分析了风速脉动对起尘量的影响。结合天津港煤堆场计算实例，给出了天津港地区的风速脉动修正系数。计算表明考虑风速脉动修正系数的计算结果比原计算结果高出8%。风速脉动修正系数的引入对于更加准确的预测与评估由煤堆场扬尘引起的空气污染有重要意义。

AR模型；脉动风速修正系数；天津港

0 引言

天津港是我国沿海主枢纽港和综合运输体系的重要枢纽，是京津冀现代化综合交通网络的重要节点和对外贸易的主要口岸，承担了大量煤炭矿石的运输、中转和存贮任务，每年因扬尘造成的物料损失和环境污染十分严重。因此研究堆场起尘规律，采取有效措施，对于减少物料损失，降低环境污染具有重要意义。

1 起尘量计算公式

1.1 起尘量定义

起尘量计算内容包括静态起尘和动态起尘两方面。静态起尘是指静置状态的堆料在风力作用下的起尘，动态起尘是指堆取料过程中产生的扬尘。本文主要讨论静态起尘的计算方法，以下不做特殊说明的起尘量均指静态起尘量。

1.2 公式的提出及其局限性

2011年，在借鉴了近年来国内外相关领域的研究成果后，交通运输部发布了修订的JTS 105-1—2011《港口建设项目环境影响评价规范》[1]（以下简称《规范》），替代了原97版《规范》。新《规范》重新修订了煤堆场静态起尘量计算公式：

Q1=0.5α（U-U0）3S （1）

U0=0.03e0.5w+3.2 （2）

其中α为货物类型起尘调节系数，新版《规范》给出了6种不同货物类型的取值，依据不同情形选取不同参数。

1.3 新版《规范》公式使用中的一些问题

新的源强计算公式考虑了不同煤种以及煤堆表面积对起尘量的影响，起尘因素考虑的更为全面。

但通过分析发现新的《规范》源强公式在使用中仍然存在以下一些问题：

1）Q1的量纲。根据公式的组合项推断，其量纲应为“质量/（时间·面积）”，公式中对时间没有明确的规定，在实际应用中有取mg/（s·m2），kg/a，也有取kg/（h·m2）。公式单位不明确会对使用者造成困扰，本文的讨论中统一使用的单位为g/（h·m2）。

2）含水率w。之前的大量研究总结的起尘量计算公式中的含水率一般指煤堆的表层含水率，但表层含水率究竟应该取多大深度处的煤尘，每个研究不尽相同，本文倾向于文献[2]的结论，即煤堆表层的含水率应取自煤堆表面至其以下1 cm部分的含水率[2]。

3）堆场风速U。堆场风速是指风掠过煤堆表面的水平速度，是一段时间内的平均值。堆场风速在使用中存在两个问题。

首先是风速的位置不明确，即取哪一个位置的风速进行计算。按照《规范》的定义，风速应取整个煤堆高度范围内的掠过煤堆表面的风速，但是在复杂的堆场作业环境下，实时监测煤堆表面各个高度处的风速显然不现实，因此在实际工作中一般只考虑煤堆顶面的风速[3]。

风速数据一般采用附近气象站或者当地海事部门提供的数据。气象站提供的风速风向一般是离地面10~12 m的高度测量得到的，而港口露天煤堆场的堆存高度一般为6~8 m，一些煤堆也会堆到10 m以上，为了得到与煤堆高度相对应的风速数据，可以采用风速的垂直风梯度的分布规律对风速进行折算。

常用的垂直风速分布规律有两种：对数率和指数率。观测研究表明[4]：指数率误差小于对数率，且指数率形式简单，因此在研究煤堆起尘问题中，一些学者建议参照我国GB 50009—2012《建筑结构荷载规范》[5]中规定的指数率进行有关的计算。表达式如下：

其次，采用平均风速定义的堆场风速U，在计算中会造成误差。《规范》规定“排放量和风速相关的污染物宜按多年平均风速计算污染源强”，天津港地区近30 a的10 m高平均风速为3.8 m/s，但是一般煤炭和矿粉堆场的起尘风速都在4.3~4.7 m/s之间[2]，若按《规范》公式计算起尘量为0，显然与实际不符。原因在于这种按照平均风速计算起尘量的方法忽略了风的脉动特征，实际风速并不是一个常量，而是围绕某个数值上下波动，可以看成平均风速和脉动风速的叠加，两部分相加之和若大于起动风速，则引起煤尘排放，否则不引起排放。

研究认为，自然风速的脉动服从高斯分布[6]，假设存在一段平稳随机风速序列，均值为U，上下波动幅度为δ，时间长度为t，将时间N等分，其中N充分大，每份时长Δt。由于N充分大，因此在Δt时间内的起尘量可近似按下式计算：

ΔQ=0.5αS[U（t）-U0]3Δt （4）

由于自然脉动风速服从高斯分布，因此在以U为均值的脉动风速序列中风速U+δ与U-δ这两个值是等可能出现的。对比图1的y=（U-U0）3的图像可以发现，由于图像在第一象限为凹函数，因此必有y（U+δ）+y（U-δ）>2y（U）。亦即在相同时间内，按照平均风速计算的起尘量一定低于按照脉动风速计算的起尘量，即：

ΔQ（U+δ）+ΔQ（U-δ）>2ΔQ（U） （5）

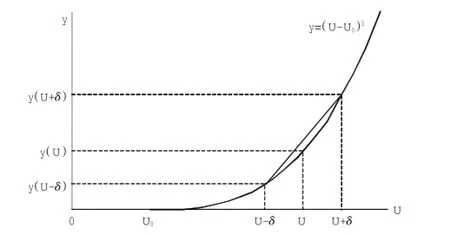
图1 y=（U-U0）3图像Fig.1 Graph of the function y=（U-U0）3

因此，《规范》公式采用平均风速的计算方法存在系统性误差。

为了尽量消除这个误差，下面采用模拟风速时程和对比计算的方法引入风速脉动修正系数对规范公式的计算结果进行修正。

2 模拟脉动风速时程

2.1 脉动风速时程的模拟方法

由阵风功率谱模拟脉动风速时程是确定阵风对起尘量影响系数的关键，目前模拟脉动风速时程的方法主要有4种[7-8]：线性滤波法，谐波叠加法，逆Fourier变化法，小波分析法。本文采用线性滤波法中的自回归模型（Auto-Regressive，AR）。AR模型因其计算量小、速度快，易于编程的特点，被广泛用于分析随机振动和时间序列，该模型描述M个空间相关点脉动风速时程的表达式如下：

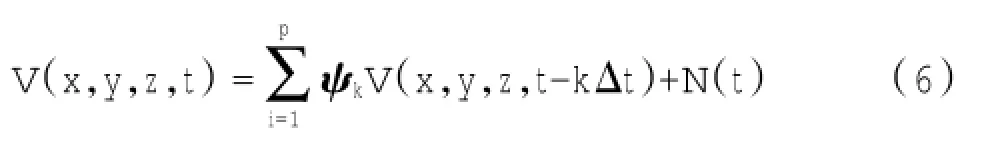
式中：V（x，y，z，t）、V（x，y，z，t-kΔt）为脉动风速向量；ψk为自回归系数矩阵；N（t）为均值为0的平稳随机过程。下面就AR方法使用过程中的几个关键点展开论述。

2.2 功率谱的选择

首先确定脉动风自功率谱。我国规范采用的是Davenport谱[5]，表达式如下：

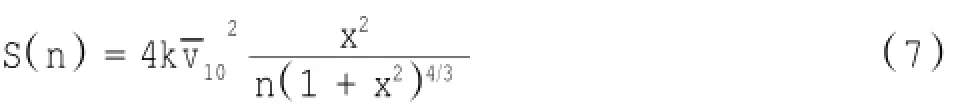
式中：k为地面粗糙度系数，依据地面类型查表取值。我国《建筑结构荷载规范》虽然将地形划分为四类，但并未明确给出Davenport风谱中系数k对应每种地形的取值，参考文献[9]的研究，对应于A类地形，即近海海岸地区，本文取为0.001 29。

2.3 确定空间相关函数

我国《建筑结构荷载规范》采用的是Shiotani提出的与频率无关的三维空间相干函数，但相关研究表明其与实际情况差别较大[10]，因此本文采用考虑了频率与风速因素的Davenport相关函数，表达式如下：

3 求解风速脉动修正系数

下面以天津港某临近海边的堆场为例，结合具体算例给出风速脉动修正系数。

3.1 求解全年风速分布概率

本文采用韦伯分布函数，其计算结果的相关系数通常在0.95以上，能较好地模拟实际风速分布。主要计算参数如下：

堆场内煤堆的平均堆高为10 m，形状为圆锥堆，堆场面积26万m2，堆存能力176万t，年通过设计能力4 300万t。取得当地近30 a的气象统计资料，全年平均风速3.8 m/s，极大风速36.7 m/s。

韦伯分布的概率密度函数如下：

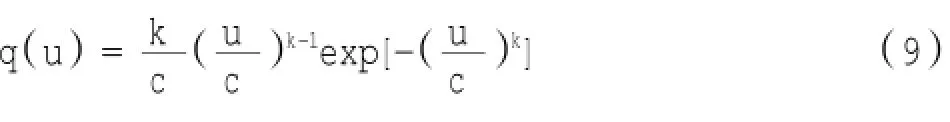
概率分布函数为：

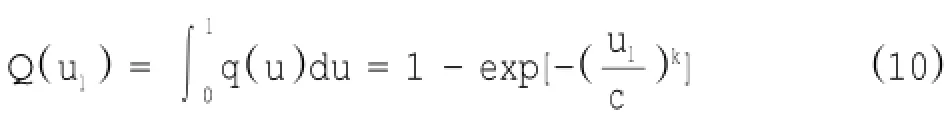
各风速段概率为：

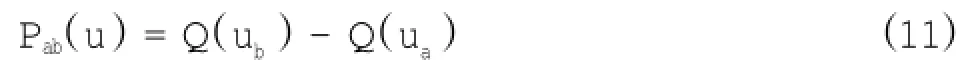
各风速段的平均风速为：

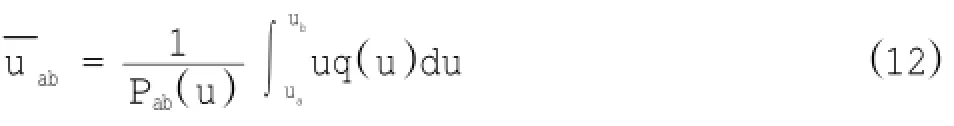
采用韦伯分布函数计算公式（9）~（12）计算得到当地的风速概率分布表如表1所示，其中98%的风速小于13.45 m/s。

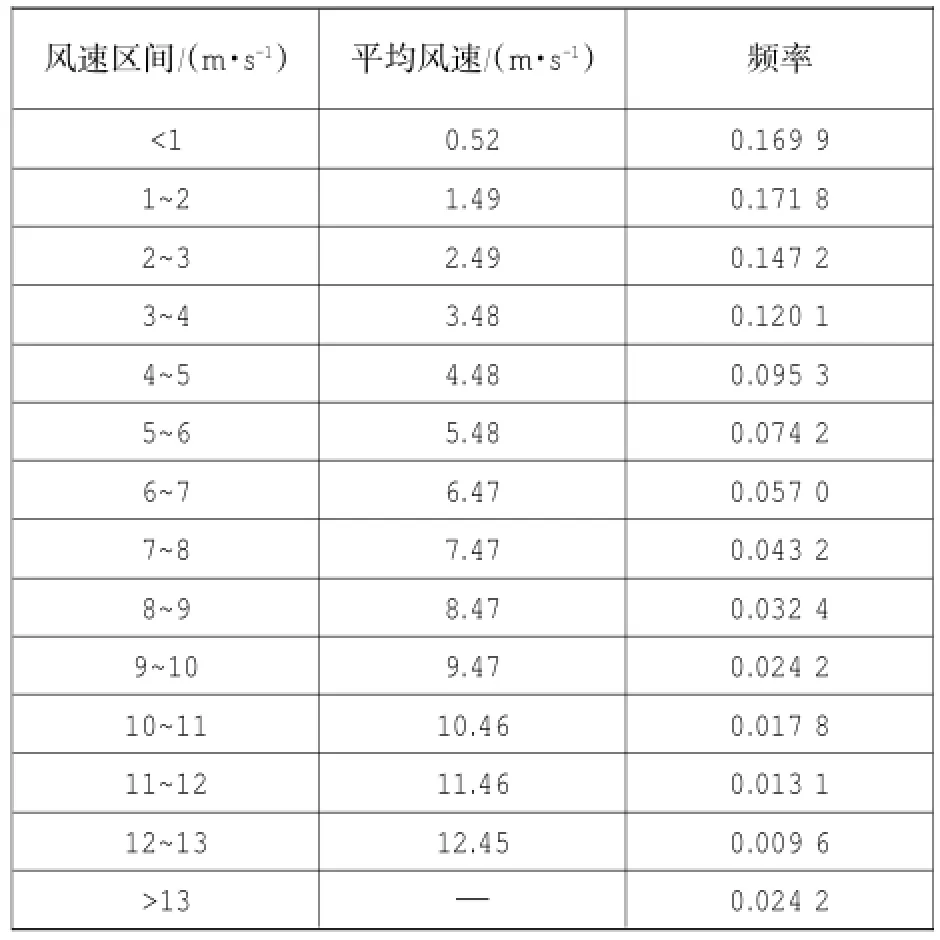
表1 风速概率分布表Table 1 Probability distribution of wind speed

3.2 求解脉动风速时程

AR模型的主要计算参数设置见表2。

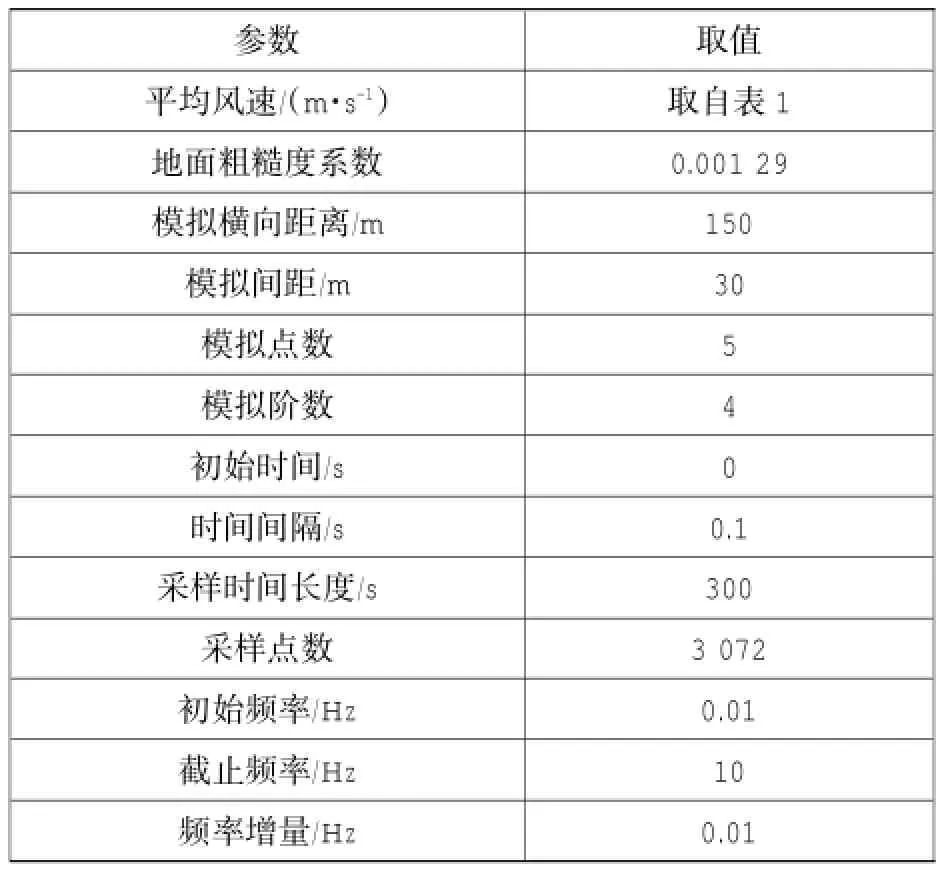
表2 AR模型的计算参数Table 2 Calculation parameters of AR model

将表2参数写入MATLAB计算程序中，调用Figure命令画出风速时程图和功率谱图。这样就得到了各点在所有风速段下的风速时程图，限于篇幅，本文只截取了第1点在v=12.45 m/s时以及第3点在v=20.4 m/s时的风速时程图和功率谱图，见图2、图3所示。

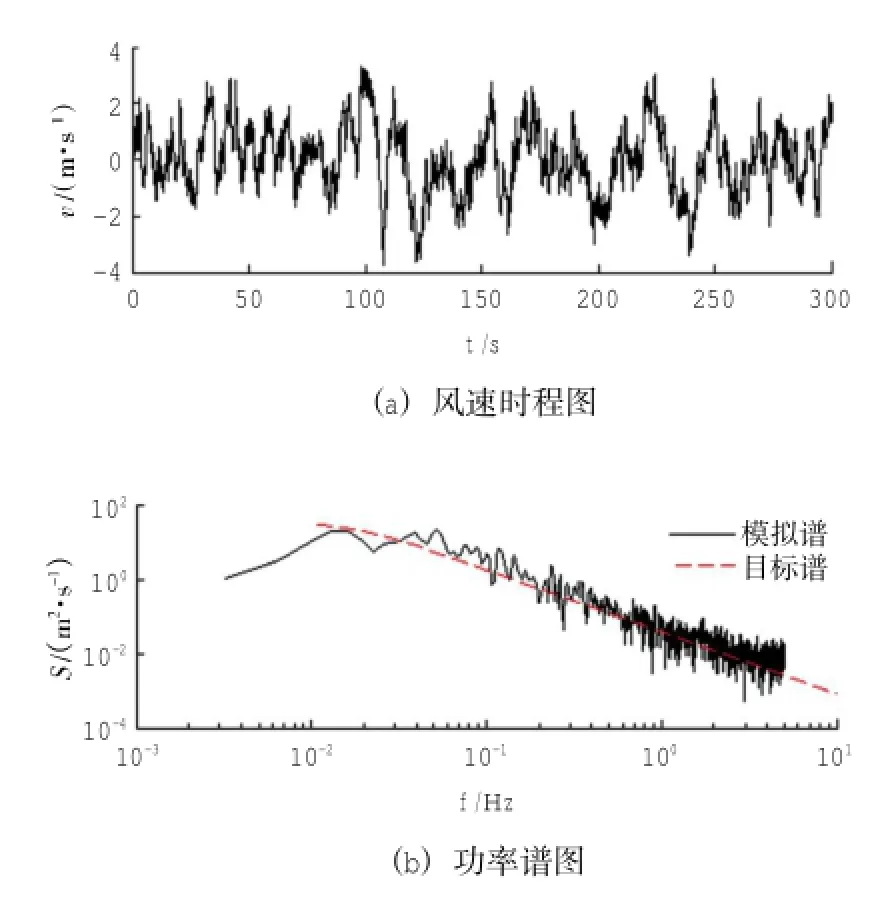
图2 第1点处脉动风速时程曲线及功率谱比较（=12.45 m/s）Fig.2 Comparisonoftimehistorycurvesandpowerspectra of fluctuating wind speed at Point 1（=12.45 m/s）

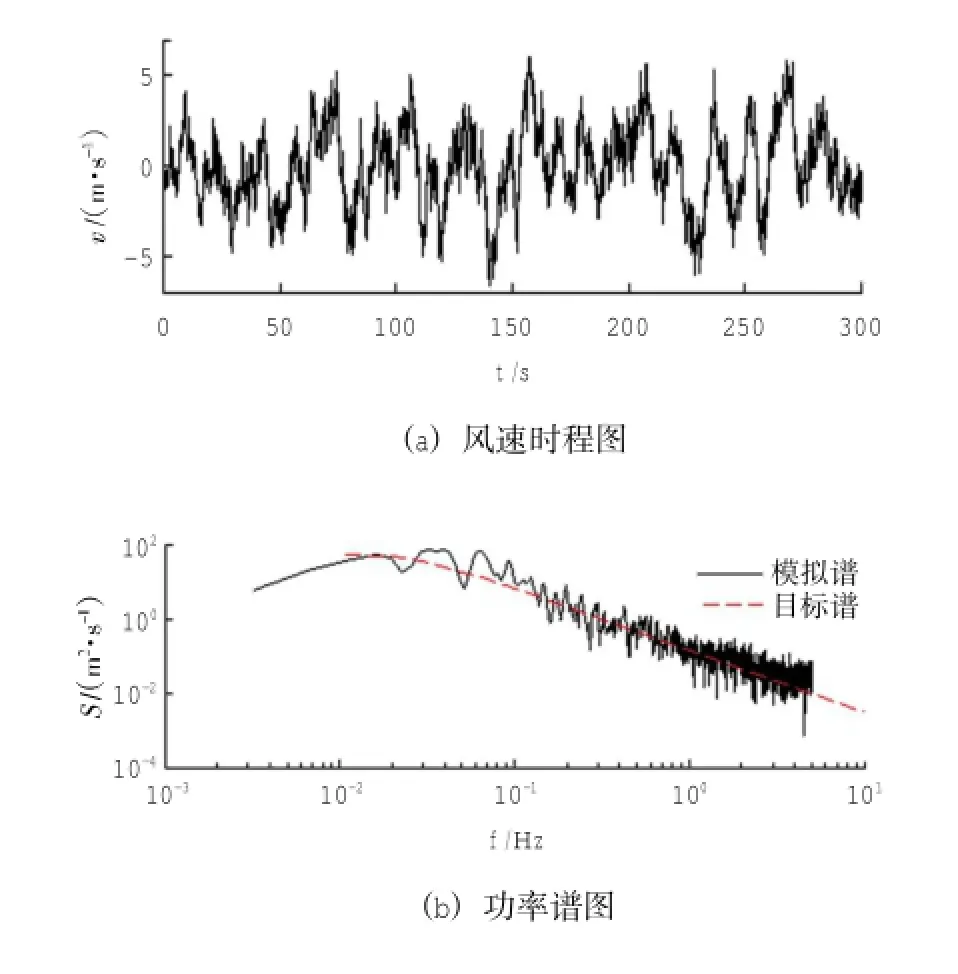
图3 第3点处脉动风速时程曲线及功率谱比较（=20.4 m/s）Fig.3 Comparisonoftimehistorycurvesandpowerspectra of fluctuating wind speed at Point 3（=20.4 m/s）

3.3 计算风速脉动修正系数

对比图中目标谱和模拟谱曲线可以看出二者的拟合程度较好。图2与图3中的风速时程为300 s，研究发现自然风速的脉动周期约为3~6 min[11]，因此本文的采样时间长度设为5 min，符合自然风速脉动的实际情况。

得到各平均风速下的脉动风速时程之后，将平均风速和脉动风速的和带入公式（5）可以得到300 s内由脉动风速引起的起尘量，进而线性外推至1 h的情况，可得各平均风速下的时均起尘量，再结合风速概率分布表计算出煤堆场的年排放总量，将结果乘以PM10的粒径百分数4%得到PM10年风蚀排放量[12]。5个不同位置计算的PM10年排放总量见表3。

表3 PM10年风蚀排放量Table 3 Average annual discharge of PM10

不考虑风速脉动，采用平均风速计算得出的PM10年排放总量为284 t/a。可以看出，考虑风速脉动的情况比后者平均多出了8%，显然风速脉动对煤堆场起尘量的计算有较大影响。

4 结语

1）脉动风速时程的合理模拟是得到准确煤尘排放强度的关键，准确模拟脉动风速时程基于可靠的气象数据，包括逐时气象预报资料等等。本文基于AR模型模拟脉动风速时程，较之于其他方法如谐波叠加法，小波分析法等，原理更为简单，易于编程，且计算速度快。

2）从实际模拟结果来看，在考虑了风速脉动之后，原本在起动风速4.19 m/s以下的风速段对起尘量依旧没有贡献。这和此前的预期有所不同，原因在于低风速段首先风速基数小，其次风速波动也不大。

3）脉动风速对起尘量的贡献主要集中在5.47 m/s到16.43 m/s之间，这一风速区间的风速基数与风速波动都比较大。考虑风速脉动的计算结果比按照平均风速计算的结果高8%，而5.47 m/s到16.43 m/s这一风速段产生的起尘量占到了增量的82%。

在更高的风速段，由于风速概率很小，且风速波动也较小，所以与按照平均风速计算的起尘量相差不大。

4）本文通过实测气象资料和MATLAB数值模拟得出风速脉动对煤码头起尘量的贡献，得出天津港地区煤码头起尘量计算的风速脉动修正系数为1.08。

[1]JTS 105-1—2011，港口建设项目环境影响评价规范[S]. JTS 105-1—2011,Specifications for environmental impact assessment of port engineering[S].

[2]张晋恺.港口散货堆场起尘规律研究[D].天津：天津大学，2012：40. ZHANG Jin-kai.Research on incipient motion of dust for bulkcargo storage yard of Harbors[D].Tianjin:Tianjin University,2012: 40.

[3] 易海涛.堆场扬尘计算和防风效率的几个问题[J].环境科技，2014（3）：46. YI Hai-tao.Some problems on the calculation of the dust and the efficiency of the wind in the yard[J].Environmental Impact Assessment,2014(3):46.

[4]李鹏，田景奎.不同下垫面近地层风速廓线特征[J].资源科学，2011，33（10）：2 006. LI Peng,TIAN Jing-kui.Characteristics of surface layer wind speed profile over different underlying surfaces[J].Resources Science,2011,33(10):2 006.

[5]GB 50009—2012，建筑结构荷载规范[S]. GB 50009—2012,Load code for the design of building structures [S].

[6] 张云彩，姚美旺，王敏生，等.阵风及其谱模拟[J].海洋工程，1996，14（2）：20. ZHANG Yun-cai,YAO Mei-wang,WANG Min-sheng,et al.Gust and its spectrum simulation[J].The Ocean Engineering,1996,14 (2):20.

[7] 刘锡良，周颖.风荷载的几种模拟方法[J].工业建筑，2005，35（5）：81-84. LIU Xi-liang,ZHOU Ying.Numerical simulation methods of wind load[J].Industrial Construction,2005,35(5)：81-84.

[8]白泉，朱浮生，康玉梅.风速时程数值模拟研究[J].辽宁科技学院学报，2006，8（1）：1-2. BAI Quan,ZHU Fu-sheng,KANG Yu-mei.Research into the numerical simulation of wind velocity histories[J].Journal of Liaoning Institute of Science and Technology,2006,8（1）：1-2.

[9]王修琼，崔剑锋.Davenport谱中系数K的计算公式及其工程应用[J].同济大学学报，2002，30（7）：851. WANG Xiu-qiong,CUI Jian-feng.Formula of coefficient K in expression of davenport spectrum and its engineering application[J]. Journal of Tongji University,2002,30(7):851.

[10]张红星，叶丰，顾明.顺风向脉动风速及风压相干性的试验研究[C]//全国振动理论及应用学术会议.2003. ZHANG Hong-xing,YE Feng,GU Ming.Experimental investigation on the coherence of characteristics of along-wind fluctuating wind velocity and wind pressure[C]//National Conference on vibration theory and Applcation.2003.

[11]程雪玲，胡非，曾庆存.格子玻尔兹曼方法模拟大气边界层中的阵风结构[J].中国科学，2012，57（10）：846. CHENG Xue-ling,HU Fei,ZENG Qing-cun.Simulation of wind gust structure in the atmospheric boundary layer with lattice Boltzmann method[J].Chinese Science Bulletin,2012,57(10):846.

[12]黄晨，李世健.煤炭堆场风蚀起尘源强两种计算方法的对比[J].中国港湾建设，2015，35（10）：50. HUANG Chen,LI Shi-jian.Contrast of two calculation methods of wind erosion dust source in coal yard[J].China Harbour Engineering,2015,35(10):50.

Error analysis and improvement of standard formula of dust calculation in coal storage yard

YANG Tao1,LIU Liang-zhi2,ZHU Ping2
（1.Construction Engineering College,Tianjin University,Tianjin 300072,China; 2.Tianjin Beiyang Water Transport&Hydraulic Survey and Design Institute Co.,Ltd.,Tianjin 300450,China）

We analyzed the standard formula for dust calculation in the coal yard based on Specifications for environmental impact assessment of port engineering,and offered some advices with regard to some problems in using these methods. Especially in combination with the AR numerical model(Auto-Regressive),the impact of wind speed fluctuation on the amount of dust was quantitatively analyzed by MATLAB.It gives the correction factor of the wind speed fluctuation by interpreting a case of a coal yard in Tianjin port.It indicates that the outcomes which takes account of the correction factor of the wind speed fluctuation is 8%higher than that which doesn't with the standard formula.So it has a profound meaning of the introduction of the correction factor of the wind speed fluctuation in predicting and evaluating the air pollution caused by the dust emission of the coal yard.

AR numerical model;correction factor of the wind speed fluctuation;Tianjin Port

U656.133；X513

A

2095-7874（2016）12-0014-05

10.7640/zggwjs201612003

2016-09-09

2016-10-21

杨涛（1991— ），男，天津市人，硕士研究生，水利工程专业，研究方向为岩土工程。E-mail：ytyyghh@163.com