利用时域配点法的卫星相对运动周期轨道求解研究

兰宇馨,岳晓奎

(西北工业大学 航天学院,陕西 西安 710072)



利用时域配点法的卫星相对运动周期轨道求解研究

兰宇馨,岳晓奎

(西北工业大学 航天学院,陕西 西安 710072)

为更精确而有效地求解卫星相对运动周期性轨道，提出了一种新的数值求解方法，该法是基于时域配点(TDC)方法研究存在J2项的非线性相对运动模型的周期解。在TDC方法中，预先将期望得到的周期解假定为傅里叶级数展开，再将傅里叶级数展开形成的近似解代入原非线性方程中，得到剩余误差函数并令其等于0，其本质是一种平衡剩余误差的方法。可通过此方法用C-W方程或T-H方程的相对运动轨道的初始条件生成边界轨道。TDC方法较一般的数值方法更精确。数值仿真表明：应用TDC方法后，能获得闭合的相对运动轨迹。研究对解决相对运动轨道维持中节省燃料和编队飞行动力学有重要的意义。

时域配点法； 卫星相对运动； 非线性代数方程组； 牛顿法； 周期解; 数值方法；J2摄动； C-W方程

0 引言

近年来，卫星在地球轨道上的相对运动研究引起了越来越多的关注。对两个在轨卫星的相对运动问题，已建立了多种模型，并将其用于不同空间任务。首先得到发展、最著名的相对运动数学模型是Clohessy-Wiltshire(C-W)方程，在解决交会问题时有很高的实用价值[1]。但C-W方程使用了一些假设条件，引起模型存在误差，这些误差是不能被忽略的：C-W方程提供的初值条件，仅在圆形参考轨道、地球为球形、线性重力加速度同时满足时才有效。由于周期相对运动轨道对相对运动的维持和航天器编队飞行来说十分重要，有必要建立更精确的相对运动模型以寻找周期性轨道。大量研究致力于不断扩展C-W方程[2-3]。但当考虑非线性微分重力、J2摄动和大偏心率的影响时，这些研究所用的初始条件就无法使用。XU，WANG提出了一种衍生的卫星相对运动的动力学模型，该模型考虑了J2摄动、重力势的非线性项，以及偏心率的影响[2]。因动力学方程中不存在任何近似，故这是一种精确的带J2项的非线性相对运动模型。本文采用了上述动力学模型，并结合TDC方法研究周期性相对运动轨道。TDC方法由代红华等提出，其本质是一种平衡剩余误差的方法，该算法已成功用于解决多种非线性动力学问题[3-6]。在TDC方法中，期望得到的周期解被预先假定为傅里叶级数展开，并将傅里叶级数展开形成的近似解代入原非线性方程中，得到剩余误差函数[7-8]。再令剩余误差函数在选定的配点范围内等于0，就获得了一组非线性代数方程，这些方程中都含有傅里叶系数作为变量，并均可用成熟的方法求解，如经典的牛顿迭代(Newton-Raphson)方法。在以前的研究中，TDC方法主要用于求解范德波振荡方程(Van der Pol oscillator)和达芬方程(Duffing oscillator)的周期解，本文对TDC方法进行拓展，以近似求解周期性相对运动轨道的初值。在轨道近似为圆形且无J2摄动时，这些初始条件能由C-W方程直接获得，但在摄动的影响下，就必须对C-W方程给出的初值进行修正，可通过用TDC方法对初值进行调整使其配适摄动的影响。为此，本文对用TDC方法的卫星相对运动周期轨道求解进行了研究。

1 TDC方法在周期性轨道问题中实现原理

为实现TDC方法，考虑一含部分展开项的傅里叶级数构成的函数，用于近似方程的周期解，该函数可表示为

f2ncos(nωft)).

(1)

式中：N为近似用到的谐波数；ωf为周期运动假定的频率；fi(i=1，2，…，2N)为谐波系数；f0为f(t)的初值[9]。显然，TDC方法求得的结果本身就是周期性变化的。

在f(t)的1个周期T内，采集K个等分区间点处的函数值f(tj)(j=1，2，…，K)，则由式(1)可得

f2ncos(nωftj)).

(2)

可发现，2N+1个系数fi配置点处的f(tj)存在转换关系

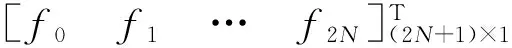
(3)

为便于表达，定义矩阵

(4)

则，如能得到K个等分区间点处的函数值f(tj)，就能确定谐波系数fi，即

[f0f1… f2N]T=

E-1[f(t1) f(t2) … f(tK)]T.

由式(1)，f(t)对时间的一阶导数可写为

cos(nωft)-f2nsin(nωft)).

(5)

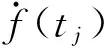
f2nsin(nωftj)).

(6)

[f1f2… f2N]T.

(7)

式(7)可更简洁地表示为

(8)

式中：

(9)

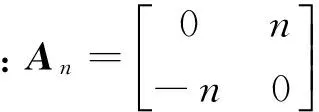
由式(3)可知：fj能通过f(tj)表示。将式(3)代入式(8)，可得

(10)

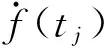
用上述转换方程推导非线性相对运动模型的TDC代数方程。图1中包含了2个笛卡尔坐标系。其中：地心惯性坐标系(ECI)由单位向量[xyz]表示；卫星轨道坐标系(LVLH)依附于参考卫星S0。

当存在J2项时，卫星Sj的相对运动在LVLH系中可表示为

(11)

图1 ECI与LVLH坐标系Fig.1 ECI and LVLH coordinate frames

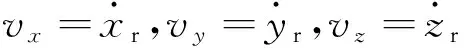
(12)

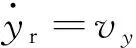
(13)

(14)

zrωzωx-(ζr-ζ)sinisinθ-

r((ηr)2-(η)2)+Fx；

(15)

(ωz)2-(ωx)2)+zrαx-

(ζr-ζ)sinisinθ+Fy；

(16)

zr((ηr)2-(η)2)-(ζr-ζ)cosi+Fz.

(17)

式中：Fx，Fy，Fz为卫星Sj在卫星LVLH系中的控制力；ζr，ηr为随相对位置xr，yr，zr变化的函数，且

(18)

此处：

(19)

式(11)与式(12)～(17)是等价的。通过增加方程数，避免了原方程中出现的二阶导数项。

考虑卫星LVLH系中的相对运动由三个方向的分量组成，且频率各异，假设

对模型进行模拟计算，可得在设计极限荷载和锚杆预拉力作用下基础各部位受力及位移变形情况，锚杆等效应力及竖向位移图、高强灌浆层第一主应力及第三主应力云图、基础混凝土第一主应力及第三主应力云图如图5—图10所示。根据应力分布云图，可以得到高强灌浆层下部附近区域、下锚板上、下部附近区域等应力，相应区域混凝土第一主应力变化曲线如图11—图13所示。

xr2ncos(nωxrt)；

(20)

yr2ncos(nωyrt)；

(21)

zr2ncos(nωzrt)；

(22)

vx2ncos(nωxrt)；

(23)

vy2ncos(nωyrt)；

(24)

vz2ncos(nωzrt).

(25)

其中xr，yr，zr，vx，vy，vz的形式与f(t)相同，但其各自相对x、y、z轴有不同的相对运动频率ωxr，ωyr，ωzr。为确定式(20)～(25)中未知的系数和频率，须从式(12)～(17)进行推导。

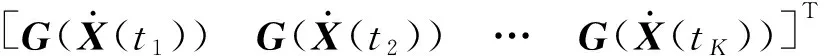
(26)

根据式(10)，式(16)的左边可转换为

(27)

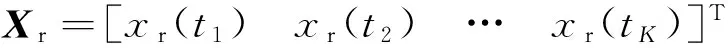
将前文的方程代入式(26)，得式(12)～(17)的时域配点法代数方程组

(28)

式中：

Q=[XrYrZrVxVyVz]T；

Ji(Q)=(R(Q′i)-R(Q))/δqi.

只要迭代向量Q确定，就能用式(26)给出的关系计算相对运动模型近似的周期解X(t)。

2 TDC方法初值选取

大量研究表明：主星轨道的偏心率会对相对运动轨道的形状产生显著影响，不仅体现在面内运动，而且包括异面运动。此外，主星轨道的高度也会影响相对运动轨迹，主要取决于空气粘滞效应的差异。本文主要关注主星轨道的偏心率和轨道倾角对相对运动的影响。

为能使牛顿迭代顺利进行，需确定迭代的初值。牛顿迭代法存在的固有局限性——迭代的初值须保证能足够接近精确解，因此本文采用成熟的相对运动模型，为TDC方法提供合适的初始迭代向量。

TDC方法的特点是能直接估计非线性系统的周期解，这是该法的优势，但同时也会带来周期运动频率ω和周期运动幅值A的初值的选取问题(此处：A即为谐波系数)。如ω，A初值估计与真实解相差太大，牛顿迭代法很有可能不会向真实解逼近，即配点应在一个接近真实周期解的函数上进行，并尽量在1个周期内配点。

在二体相对运动问题中，C-W，T-H方程能提供无摄动引力场中的相对运动周期解的初始化条件S0=[r(t0)v(t0)]，当有摄动存在时，该初始条件能提供一条近似周期的轨迹(用RK4方法就能获得)。然后用这条轨迹估计出ω，并在该轨迹上配点。

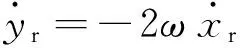
在采用了精确的J2相对运动模型后，再利用上述初始条件，就可得逐渐发散的无边界相对运动轨道。假设轨道的一个周期为T，通过采集此周期内无边界轨道上平均分布的点，就能得到TDC方法代数方程组的初始值Q0。

通常，时域配点的个数应与近似函数中的谐波系数的个数相同。由于ωxr，ωyr，ωzr未知，为求解式(28)，需要3个额外的约束。本文在起始点引入约束状态：xr(t0)=p1，yr(t0)=p2，zr(t0)=p3(p1，p2，p3是预先定义的)，则三个额外的约束状态可表示为

(29)

式(28)含配置点的位置和速度，式(29)可展开为

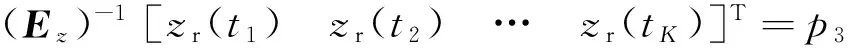
只要确定了配置点并假定频率，就能通过式(1)、(3)中的转换关系得到一条闭合的轨道。显然，该轨道开始并不能满足式(28)，但通过牛顿法或其它迭代方法，配点处的位置、速度和频率就能得以修正，最终使剩余误差达到最小。当由配点选择造成的残余误差足够小时，相应的轨道即可用于近似相对运动的周期解。

3 计算结果与分析

首先用普通的数值积分方法(RK4)求解C-W方程，得到一个发散的轨道(无非常明显的周期解)，该轨道在配点后可用TDC进行修正，其过程就是牛顿法的迭代过程。

在不同偏心率和轨道倾角条件下，1个周期内采用和未采用TDC修正的相对运动轨迹仿真结果分别如图2～5所示。

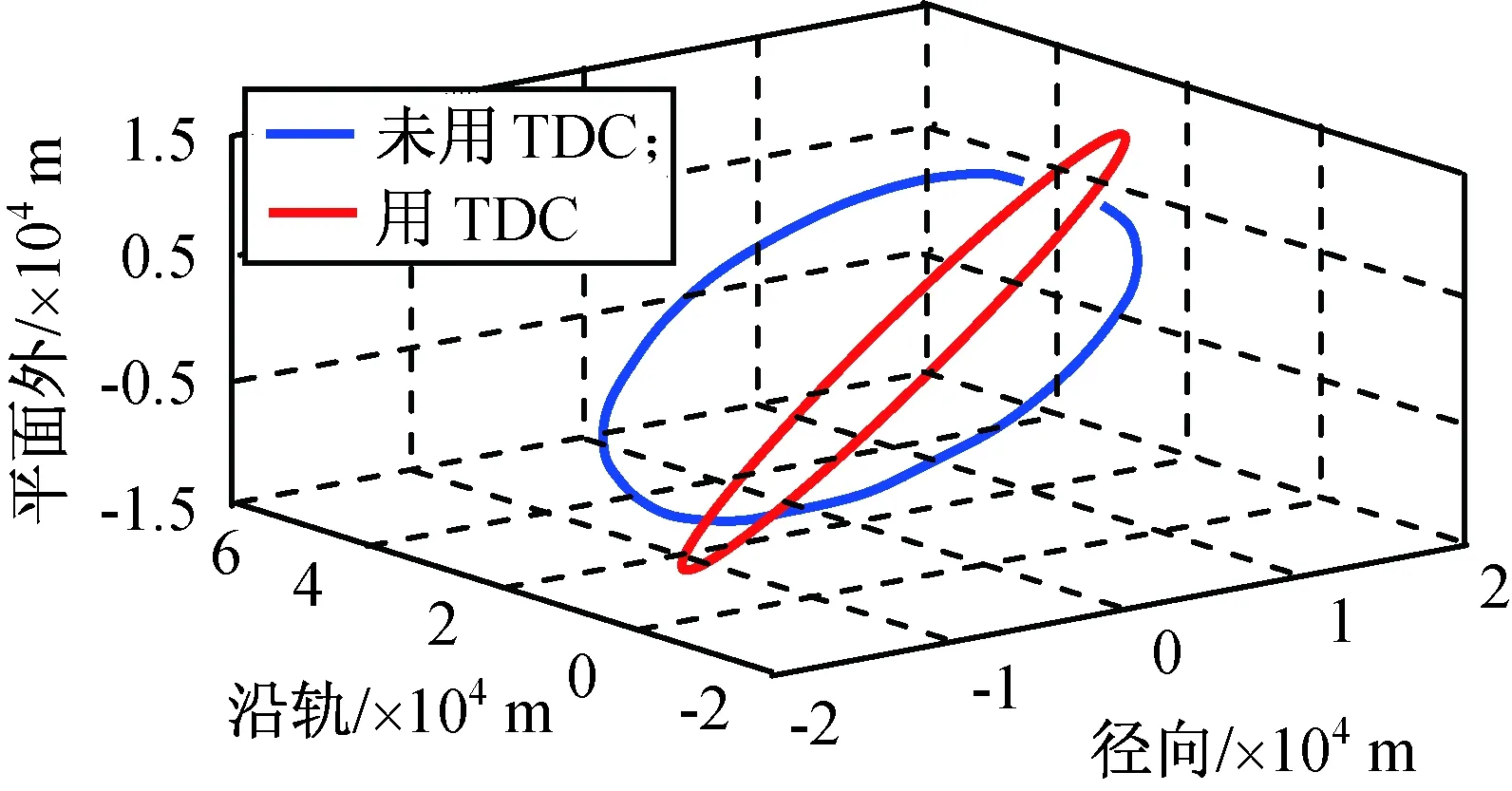
图2 e=0.02，i=π/3时采用和未采用 TDC修正的相对运动轨迹Fig.2 Relative orbit with and without correction of TDC searching scheme under e=0.02 and i=π/3

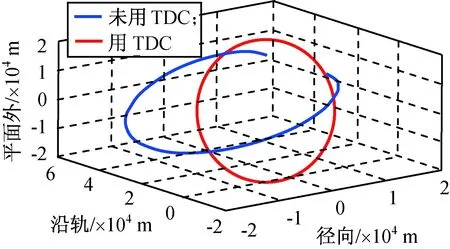
图3 e=0.05，i=π/3时采用和未采用 TDC修正的相对运动轨迹Fig.3 Relative orbit with and without correction of TDC searching scheme under e=0.05 and i=π/3

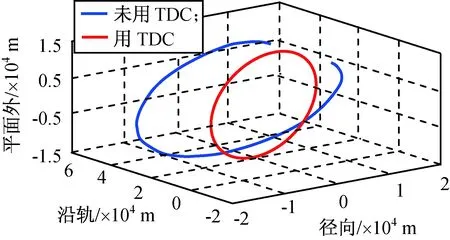
图4 e=0.05，i=0时采用和未采用 TDC修正的相对运动轨迹Fig.4 Relative orbit with and without correction of TDC searching scheme under e=0.05 and i=0

图5 e=0.1，i=π/3时采用和未采用 TDC修正的相对运动轨迹Fig.5 Relative orbit with and without correction of TDC searching scheme under e=0.1 and i=π/3

由图2～4可知：使用TDS后，相对运动轨迹就会由原来发散的状态变为封闭的曲线，当e=0.02，i=π/3时，T=7 123 s；当e=0.05，i=π/3时，T=7 130 s；当e=0.05，i=π/3时，T=7 130 s。由图5可知：当e=0.1，i=π/3时，此时轨道偏心率的值已非常大，但用TDC修正后仍获得了较理想的周期性相对运动轨道，此时T=7 157 s。

4 结束语

TDC是一种求解非线性动力学方程周期解的新方法，已成功用于求解平面二自由度翼型的振颤问题[6]。本文讨论了在J2项摄动存在时，用TDC求解在轨卫星的周期性相对运动。通过将这些周期解假设成为傅里叶级数的形式，推导出TDC的动力学方程组，再用牛顿-拉夫森迭代方法对方程进行求解。TDC的优点是能处理许多复杂方程组中的非线性项，使用较简便，结果重复性较好，发散速度很慢。理论上TDC方法还能用于解决其他的非线性问题，但由于该方法本身的特性(即在开始就假设方程组的解均为周期变化的解)，目前还局限于求解已知或有可能为周期解的方程组。若方程组本身并不存在周期解，该方法就无法适用。后续可对扩展TDC方法的适用范围进行研究。随着许多问题的动力学模型越来越精确，TDC求得周期解的精度也会越来越高，其在相对运动轨道维持中的燃料节省和保存，以及编队飞行动力学的研究中有广阔的应用前景。

[1] CLOHESSY W H. Terminal guidance system for satellite rendezvous[J]. Aerospace Sci, 1960, 27(9): 653-658.

[2] CARTER T E, BRIENT J. Optimal bounded-thrust space trajectories based on linear equations[J]. Journal of Optimization Theory & Applications, 1991, 70(2): 299-317.

[3] MELTON R G. Time-explicit representation of relative motion between elliptical orbits[J]. Journal of Guidance Control & Dynamics, 2000, 23(4): 604-610.

[4] XU G, WANG D. Nonlinear dynamic equations of satellite relative motion around an oblate earth[J]. Journal of Guidance Control and Dynamics, 2008, 31(5): 1521-1524.

[5] DAI H H, SCHNOOR M, ATLURI S N. A simple collocation scheme for obtaining the periodic solutions of the Duffing equation, and its equivalence to the high dimensional harmonic balance method: subharmonic oscillations[J]. Computer Modeling in Engineering & Sciences, 2012, 84(5): 459-497.

[6] DAI H, YUE X, YUAN J, et al. A time domain collocation method for studying the aeroelasticity of a two dimensional airfoil with a structural nonlinearity[J]. Journal of Computational Physics, 2014, 270(3): 214-237.

[7] YUE X K, DAI H H, LIU C S. Optimal scale polynomial interpolation technique for obtaining periodic solutions to the Duffing oscillator[J]. Nonlinear Dynamics, 2014, 77(4): 1455-1468.

[8] DAI H H, YUE X K, YUAN J P. A time domain collocation method for obtaining the third superharmonic solutions to the Duffing oscillator[J]. Nonlinear Dynamics, 2013, 73(73): 593-609.

[9] WANG W, YUAN J, ZHAO Y, et al. Fourier series approximations toJ2-bounded equatorial orbits[J]. Mathematical Problems in Engineering, 2014: 1-8.

[10] KASDIN N J, GURFIL P. Hamiltonian modelling of relative motion[J]. Annals of the New York Academy of Sciences, 2004, 1017(1): 138-157.

Study on a Time Domain Collocation Method to Search for Periodic Orbits of Satellite Relative Motion

LAN Yu-xin, YUE Xiao-kui

(School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, Shaanxi, China)

To study for the periodic orbits of satellite relative motion, a new numerical approach was proposed, based on using the time domain collocation (TDC) method to search for the periodic solutions of an exactJ2nonlinear relative model. In TDC method, the desired periodic solution was preassumed as a truncated Fourier series first, then the approximate solution of the Fourier series was substituted into the equations of nonlinear system, resulting in a residual error function, which was essentially one of the weighted residual methods. The initial conditions for periodic relative orbits of the Clohessy-Wiltshire (C-W) equations or Tschauner-Hempel (T-H) equations could be refined with this approach to generate nearly bounded orbits. Numerical simulations show that the presented TDC searching scheme is more precise. It is obvious that the TDC searching scheme gives the closed orbit of relative motion. Consequently, it is believed that this approach has potential applications on fuel saving relative orbit maintenance and spacecraft formation flying.

Time domain collocation method; Satellite relative motion; Nonlinear algebraic equations; Newton method; Periodic solutions; Numerical simulationslJ2perturbation; C-W equations

1006-1630(2016)05-0095-06

2016-07-20；

2016-09-12

国家自然基金资助(11502203)

兰宇馨(1991—)，男，硕士生，主要研究方向为飞行器设计、非合作目标捕获和轨道力学。

V412.41

A

10.19328/j.cnki.1006-1630.2016.05.015