谐振式光子带隙光纤陀螺谐振腔方案设计

冯丽爽,焦洪臣,姜 辉,傅长松

(1.微纳测控与低维物理教育部重点实验室,北京 100191; 2.上海惯性工程技术研究中心,上海 200233;3.上海航天控制技术研究所,上海 201109)



谐振式光子带隙光纤陀螺谐振腔方案设计

冯丽爽1,焦洪臣1,姜 辉2、3,傅长松2、3

(1.微纳测控与低维物理教育部重点实验室,北京 100191; 2.上海惯性工程技术研究中心,上海 200233;3.上海航天控制技术研究所,上海 201109)

为提高陀螺系统的精度，设计并实现了基于光子带隙光纤的谐振式光学陀螺方案。对用于该陀螺的核心器件谐振腔进行了研究，仿真比较了反射式和透射式两种谐振腔的清晰度和信噪比，发现反射式的清晰度高、输出信号强度大，由此确定谐振腔采用反射式结构方案。以谐振腔极限灵敏度为优化参考值，根据谐振腔频率响应特性和陀螺数据输出特性，仿真优化了谐振腔腔长、耦合器分光比等结构参数。在极限灵敏度极值对应的最佳分光比为约0.5时，谐振腔长取30 m，陀螺极限灵敏度达0.03 (°)/h，完成光子带隙光纤谐振腔的理论设计。

光纤陀螺； 谐振腔； 光子带隙光纤； 反射式； 透射式； 熔接损耗； 信噪比； 极限灵敏度

0 引言

惯性导航与制导是精确打击武器和平台实现自主导航、制导的核心，其性能对武器装备的精度、机动性、突防和生存能力等有决定性影响，而陀螺是惯性导航与制导系统的核心仪表，是决定惯性系统性能的最主要因素[1]。从传统机电式陀螺到激光陀螺再至光纤陀螺，历经数十年发展，光纤陀螺在惯性技术领域的地位已经确立，其全固态结构，使之较以往采用机械转子或气体环形激光器的方案更具优势，可实现高可靠、长寿命、快速起动、大动态范围的应用。干涉式光纤陀螺已进入实用化阶段，与其相比，实现相同的灵敏度，谐振式光纤陀螺所需的光纤长度可缩短很多，这体现了将来陀螺高精度、小型化的发展趋势，也是新型光纤陀螺研究的热点和重点[2-3]。空芯光子晶体光纤利用周期排列的空气孔包层结构，形成光子带隙效应，将光限制在空芯中传输，其内部一般是空气、其它气体或真空，而瑞利背向散射、克尔非线性效应及维尔德常数在空气、其它气体或真空中非常小，空芯光子晶体光纤从根本上抑制了由导光介质引入的各种非互易噪声，有望极大地改善谐振式光纤陀螺的性能[4-5]。

谐振式光子带隙光纤陀螺方案综合了谐振式光纤陀螺的优势和光子带隙光纤的导光机理优势，有望解决目前传统谐振式光纤陀螺面临的背散噪声、克尔噪声和偏振噪声等问题。光子带隙光纤谐振腔作为谐振式光子带隙光纤陀螺的核心器件，其性能直接决定了陀螺系统的最终精度。因光子带隙光纤导光机理与传统光纤存在本质区别，其与传统光纤器件的结连使用需特殊处理，这同时造成谐振腔性能与器件参数间的对应关系存在特殊性，需结合光纤特性及陀螺灵敏度需求，对谐振腔结构及器件参数进行合理优化设计[6]。谐振腔结构及器件研究中，主要关注的是异种光纤的高可靠、低损耗连接，耦合器参数选择，以及谐振腔整体方案的选择，不仅需从谐振腔性能要求对器件结构进行设计，而且要考虑谐振式光纤陀螺输出信号特征，结合光纤特性及陀螺灵敏度需求，对谐振腔结构及器件参数进行合理优化设计。考虑陀螺稳定性及环境适应性，设计使用传统保偏光纤拉锥耦合器分光，腔内采用异种光纤熔接方式引入光子带隙光纤，本文对一种用于谐振式光子带隙光纤陀螺的谐振腔方案进行了研究。

1 谐振腔结构设计

谐振式陀螺使用的光纤谐振腔可分为反射式和透射式两种，对应光子带隙光纤谐振腔结构如图1所示[7]。比较两者的结构，反射式腔包含一个光纤耦合器，而透射式腔包含两个光纤耦合器。考虑光子带隙光纤难以进行研磨、拉锥等二次加工，结构中耦合器为实心保偏光纤制作。

图1 谐振腔结构Fig.1 Resonator structure

当采用光子带隙光纤绕制光纤环时，需将其与实心保偏光纤耦合器进行熔接。由图1可知：因腔内熔点的存在，反射式与透射式谐振腔传递函数将出现差异。建立器件信号传递模型，得谐振腔振幅传递函数为

(1)

式中：R(f)，T(f)分别为反射式腔和透射式腔的传递函数；k为耦合器直通端分光比；αh为腔内熔点总损耗；αc为耦合器插入损耗；αl为光子带隙光纤传输总损耗；f为入射激光频率；n为传输模式等效折射率；L为光纤环总长度；c为真空中光速。

比较信号特征，反射式腔输出信号包含两部分分量，一部分由耦合器直接输出，另一部分经腔调制后输出，后者较前者存在相移π；透射式腔输出信号中仅有经腔调制后的分量，具有相同的附加相移[8-9]。因此，反射式腔频率响应曲线为谐振谷，透射式腔频率响应曲线为谐振峰，如图2所示。图中：横坐标为入射光频率相对谐振频率的偏移量，单位FSR为谐振腔自由普线宽度；纵坐标为谐振腔输出强度与入射光强的比值。

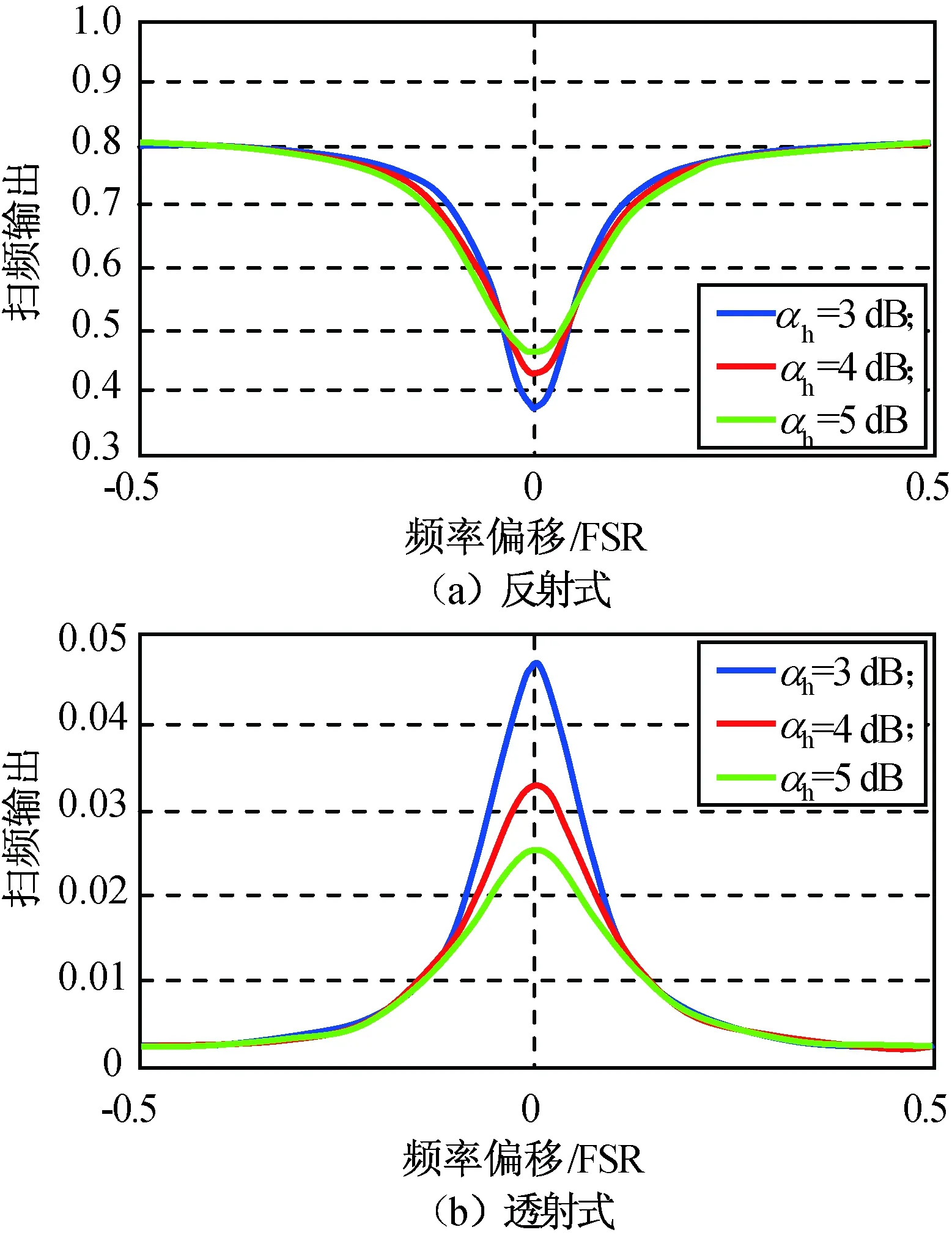
图2 谐振腔频率响应曲线Fig.2 Resonator transfer curve

假设系统噪声均来自于探测器散粒噪声，谐振腔清晰度及对应陀螺输出信噪比分别为

(2)

(3)

式中：γSNR(R)，γSNR(T)分别为反射式和透射式陀螺输出信噪比；η为探测器光电转换效率；t为输出积分时间；I0为入射光强；h为普朗克常量[10]。

在不同腔长L条件下对单熔点损耗值时反射式、透射式腔清晰度及信噪比进行仿真。设耦合器分光比0.9，光子带隙光纤单位传输损耗20 dB/km，激光器波长1 550 nm，入射光强1 mW，探测器光电转换效率0.95，输出积分时间10 s，传输模式等效折射率0.99，仿真所得两种谐振腔清晰度、信噪比及其差值分别如图3～5所示。

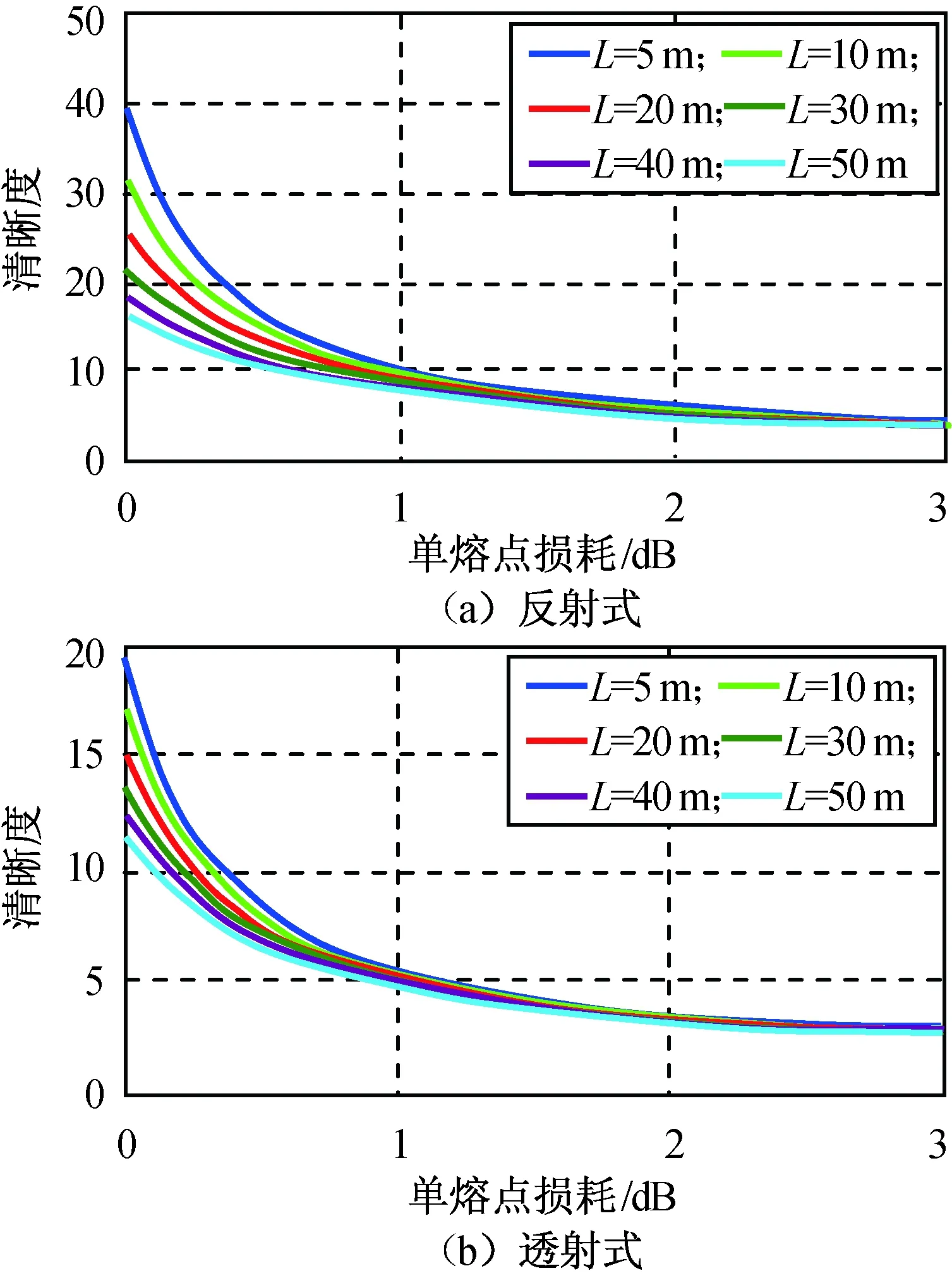
图3 谐振腔清晰度Fig.3 Fineness of resonator

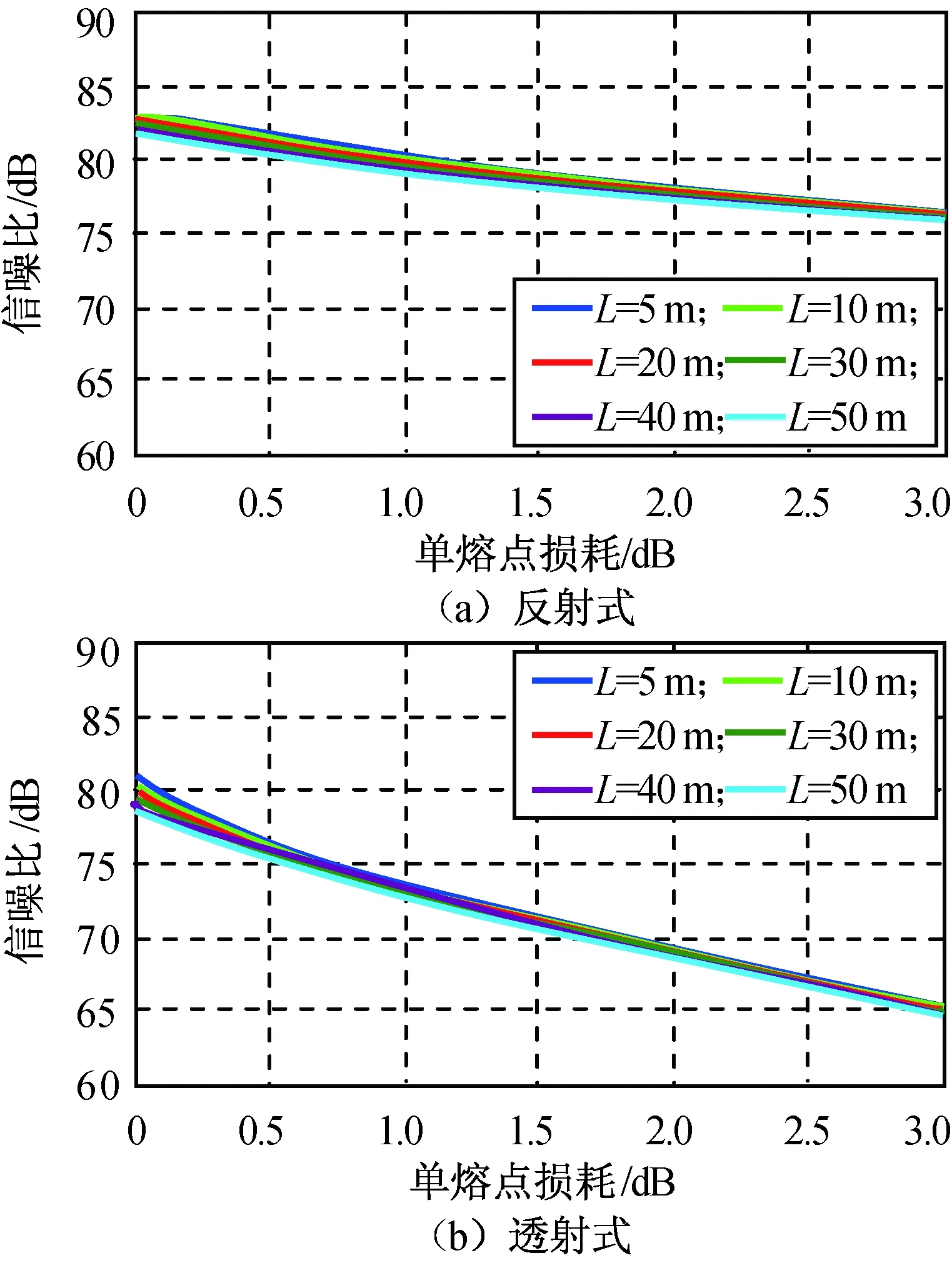
图4 谐振腔信噪比Fig.4 Signal-to-noise ratio of resonator

图5 两种谐振腔信噪比差值Fig.5 Signal-to-noise ratio difference of resonator

由图3～5可知：因反射式结构腔内熔点更少、总体损耗更小，在相同腔长及分光比条件下，其清晰度约为透射式结构的两倍。同时，由于光强透过率更高，反射式腔对应的陀螺输出信号强度更高，因此陀螺采用反射式腔的信噪比大于透射式腔，在熔点损耗较大时该现象更明显。综合两者考虑，设计选择反射式谐振腔作为陀螺敏感元件结构。

2 谐振腔参数优化与实现

谐振腔基本结构确定后，取决于探测器散粒噪声的陀螺理论精度反映了陀螺的极限性能，以此极限灵敏度作为谐振腔参数优化的参考值[11]。综合谐振腔频率响应曲线与陀螺输出特性，得到陀螺极限灵敏度

(4)

式中：λ为入射光波长；P为光纤环单圈光纤周长；A为光纤环单圈光纤包围面积；Γ为谐振腔的谐振谱线宽度。

由式(3)可知：γSNR(R)与谐振腔谐振深度呈正比。为获得较好的极限灵敏度，应取得尽量窄的Γ以及尽量大的谐振深度。

由于光子带隙光纤结构及导光机理的特殊性，在谐振腔设计中不可忽略该新型光纤与传统实心保偏光纤连接及其本身引入的附加损耗等问题。已有实验数据表明，所用光子带隙光纤传输损耗为20 dB/km，其与传统实心保偏光纤首尾一对熔点的总损耗典型值为4.1 dB[12]。根据该损耗典型值，在同样仿真条件下，得到不同耦合器分光比和光纤谐振腔腔长时谐振谱线宽度、谐振深度和极限灵敏度如图6所示。

在本文仿真参数及实验已知参数设置条件下，由式(4)可知：当分光比增大时，Γ减小，但谐振深度存在极值，因此随着分光比增大，极限灵敏度也将存在极值，同时较长的腔长可获得更窄的谱线宽度，从而改善极限灵敏度；当L增大时，在较短长度区间，传输损耗引起的总损耗增加相对已有损耗值较小，因此对清晰度或透射率影响不大，同时伴随FSR减小，使Γ急剧减小，对极限灵敏度改善效果明显，但L过长时，附加的传输损耗不可忽略，此时继续增加腔长作用不大。

综上，在取得最佳分光比的同时，应合理设计腔长。由本文仿真结果可得：对应极限灵敏度极值的最佳分光比约0.5；当L大于30 m时，极限灵敏度变化不再明显，结合两方面因素，选取分光比0.5及腔长30 m作为最终设计值，得到陀螺极限灵敏度可达0.03 (°)/h。

3 结束语

本文对谐振式光子带隙光纤陀螺谐振腔的设计进行了研究。通过比较同等参数条件下反射式结构与透射式结构谐振腔的清晰度及对应陀螺系统信噪比特性，确定了谐振式光子带隙光纤陀螺采用反射式谐振腔结构。根据异种光纤熔接损耗实验数据、合理假设谐振腔结构变量，仿真获得了谐振腔对应陀螺系统极限灵敏度与待设计参数的对应关系。综合考虑各参量的匹配，最终确定谐振腔设计腔长为30 m、耦合器分光比0.5。在此设计值下，陀螺极限灵敏度可达0.03 (°)/h。目前设计精度达到惯性级要求，但仍存在不足，关键问题集中于两点：空心光子带隙光纤制备技术有待提高，现光子带隙光纤损耗性能及批次性较传统光纤仍有较大差距；为保证期间的稳定性，设计中所用耦合方式引入了较大的腔内异种光纤对接损耗。后续研究应考虑针对以上两点，在研制光纤的同时设计兼备高稳定性与低损耗特性的光路耦合结构。解决上述两点问题后，基于光子带隙光纤的谐振式光学陀螺有望实现精密级精度，将成为未来高精度光学陀螺的重要发展方向。

图6 谐振性能和陀螺极限灵敏度仿真结果Fig.6 Simulation of resonator line width, resonance depth and limited sensitivity

[1] SANDERS S, STRANDJORD L, MEAD D. Fiber-optic gyro technology trends——a honeywell perspective[C]// 2002 15th Optical Fiber Sensors Conference. Portland: OSA, 2002: Technical Digest 1, 5-82(2002).

[2] BARBOUR N M. Inertial navigation sensors[R]. Charles Stark Draper Laboratory, RTO-EN-SET-116, 2011.

[3] 孙丽, 王德钊. 国内外光纤陀螺的最新进展[J]. 控制工程, 2002(1): 9-14.

[4] SMITH C M, VENKATARAMAN N, GALLAGHER M T, et al. Low-loss hollow-core silica/airphotonic bandgapfibre[J]. Nature, 2003, 424(7): 657-659.

[5] BROENG J, BARKOU S E, SANDERGAARD T, et al. Analysis of air-guiding photonic bandgap fibers[J]. Optics Letters, 2000, 25(2): 96-98.

[6] 陈翔. 光子晶体光纤的制备及传输特性研究[D]. 杭州: 浙江大学, 2013.

[7] 郭伟. 谐振式光纤陀螺的基础研究[D]. 杭州: 浙江大学, 2003.

[8] FENG Li-shuang, DENG Xue-wen, REN Xiao-yuan, et al. Research on hollow-core photonic band-gap fiber ring resonator based on micro-optics structure[J]. ACTA Optic Asinica, 2012, 32(8): 0806002.

[9] FENG Li-shuang, WANG Jun-jie, ZHI Yin-zhou, et al. Transmissive resonator optic gyro based on silica waveguide ring resonator[J]. Optics Express, 2014, 22(22): 27565-27575.

[10] TERREL M A. Rotation sensing with optical ring resonators[D]. Palo Alto: Stanford University, 2011.

[11] KAISER T J, CARDARELLI D, WALSH J. Experimental developments in the RFOG[J]. Fiber Optic and Laser Sensors, 1990, 1367: 121-126.

[12] THAPA R, KNABE K, CORWIN K L, et al. Arc fusion splicing of hollow-core photonic band gap fibers for gas-filled fiber cells[J]. Optics Express, 2006, 14(21): 9576-9583.

Analysis of Resonator for Resonant Optic Gyro Based on Photonic Bandgap Fiber

FENG Li-shuang1, JIAO Hong-chen1, JIANG Hui2, 3, FU Chang-song2, 3

(1. Key Laboratory of Micro-Nano Measurement, Manipulation and Physics, Ministry of Education Beihang University, Beijing 100191, China; 2. Shanghai Engineer Research Center of Inertia, Shanghai 200233, China; 3. Shanghai Institute of Spaceflight Control Technology， Shanghai 201109, China)

To improve the precision of gyro system, the resonator based on photonic bandgap fiber used in photonic bandgap fiber resonant optic gyro system was designed and implemented in this paper. The different resonators which were the key components in the gyro were studied. The fineness and signal-to-noised ratio of reflecting structure and transmission structure were compared by simulation. It found that the reflecting structure had higher finesse and higher intensity of output signal than those of the transmission structure, so the reflecting structure was selected for the resonator. According to the frequency response characteristic and gyro output signal feature, the structure parameters which were fiber length, coupler transmissivity and others were optimized while existing loss coefficient was served as optimal reference. When the optimal splitting ratio relative to limited sensitivity is about 0.5, the fiber length is 30 m and the limited sensitivity can reach 0.03 (°)/h. The theoretical design of the photonic bandgap fiber resonant has been completed.

Fiber optic gyro; Resonator; Photonic bandgap fiber; Reflecting structure; Transmission structure; Splicing loss; Signal-to-noise ratio; Limited sensitivity

1006-1630(2016)05-0084-05

2016-06-06；

2016-07-08

国家自然科学基金资助(61405005)

冯丽爽(1968—)，女，教授，主要研究方向为微小型光学惯性器件、集成光电子器件和先进光纤传感技术等。

V241.59

A

10.19328/j.cnki.1006-1630.2016.05.013