基于自组织混合模型的多变量航天产品加工过程控制方法研究
2016-12-21余建波李传锋
余建波,李传锋,吴 昊,程 辉
(1.同济大学 机械与能源工程学院,上海 201804; 2.山东省特种设备检验研究院,山东 济南 250101;3.上海航天设备制造总厂,上海 200245)
基于自组织混合模型的多变量航天产品加工过程控制方法研究
余建波1,李传锋1,吴 昊2,程 辉3
(1.同济大学 机械与能源工程学院,上海 201804; 2.山东省特种设备检验研究院,山东 济南 250101;3.上海航天设备制造总厂,上海 200245)
为解决航天产品因制造过程的随机性和动态性而在复杂的多变量加工过程中表现出非线性或多模态等特性,用传统多变量过程控制方法无法有效监控的困难,提出了一种基于自组织混合模型(SOMM)的过程监控方法,以实现非线性和多模态等过程的状态建模和在线异常监控。采用自组织映射结合混合模型,对非线性和多模态等过程状态进行建模,设置控制图阈值;提出了基于最小欧氏距离和负对数似然值的制造过程控制图,在线识别和评估制造过程运行状态。设计的基于SOMM的制造过程监控系统由离线建模和在线监控两部分组成。为验证所提方法在非线性和多模态制造过程中的监控效果,进行了两个仿真实验,并与主元分析、自组织映射等传统监控方法性能进行比较。实验结果表明所提方法在非线性及多模态过程中均有更好的过程监控性能,可用于航天产品加工过程的质量控制。
多变量制造过程; 工序质量; 统计过程控制; 过程监控; 控制图; 多模态; 非线性; 自组织混合模型
0 引言
航天产品属于复杂产品范畴,对其质量进行控制是研制生产过程中的重要组成部分。另外,航天产品不同于民用产品,前者在研制生产过程中对质量控制过程常有更高的要求。典型航空航天装备的关键部件制造一般是复杂的多变量制造过程[1]。统计过程控制作为质量控制的重要手段,一直是学术界和工业界的重点研究对象。产品质量常需用多个质量指标度量,由于各质量指标相互关联,采用Shewhart、累积和控制(CUSUM)、指数加权移动平均值(EWMA)等单变量控制图分别进行控制,易导致过高的误报率[2]。因此,应从多变量角度进行分析,从而形成了多元统计过程控制的方法。
基于主元分析(PCA)、偏最小二乘法(PLS)等模型的多变量统计过程控制方法已成功用于制造过程的在线监控[3]。这些多变量统计过程控制方法都假设正常状态数据源于同一工作状态并服从高斯分布。如PCA计算控制限时要求分解得到的得分向量符合高斯分布,但对非线性和多模态过程,因不满足这一条件,PCA将不再适用[4]。在航天产品制造过程中,由于工作条件的改变,如原材料更改、传感器变化、机器维修维护等,会使过程状态发生改变,导致过程数据呈现出非线性或多模态等特征,此时采用基于PCA的T2图和平方预测误差(SPE)图对过程进行监控,难以获得理想效果。为解决此问题,采用一种新的统计分析方法就显得尤为重要。为解决产品监控过程中出现的非线性过程和多模态过程问题进行了大量研究:提出了独立主元分析(ICA)、规范变量分析(CVA)、局部保持投影(LPP)等统计过程控制方法以弥补PCA,PLS监控模型的不足[5-7]。人工神经网络(ANN)、支持向量机(SVM)等机器学习模型也被用于解决监控过程中出现的问题并取得成功[8-10]。YU针对非线性过程和多模态过程,提出了基于隐性马尔科夫模型的MDNLLP控制图和BIP控制图以在线识别过程状态[11]。SALEHI等构建了多变量过程异常信号在线分析混合模型,对多变量过程均值的三种异常进行识别[12]。YU综合了PCA与高斯混合模型(GMM)用于非线性和多模态半导体制造过程的异常监控[13]。罗先喜等针对多模态过程,提出了先将不同状态的数据样本分组标准化,再分别进行主元分析得到不同稳态下的控制限进行监控[14]。但目前对多模态与非线性过程状态同时进行建模,并采用量化指标评估制造过程质量的状态尚未得到很好的解决。本文针对航天产品监控过程中可能出现的非线性和多模态过程的质量控制问题,典型的应用为航天复杂铝合金部件在工序加工过程、部件加工过程中的尺寸精度受到机床、夹具、刀具等变量的综合影响,这是一个典型的复杂多变量制造过程。因此,本文提出了自组织混合模型(SOMM),以对制造过程多模态与非线性数据进行统计描述建模,可克服传统的多变量统计过程方法(如基于PCA的过程监控方法)存在的无法有效监控的缺陷,并提出了欧氏距离(ED)和负对数似然值(NLLP)两种量化指标以评估过程运行状态。用两个典型仿真实验[SOMM与PCA、自组织映射(SOM)]的实验结果比较了建模和监控效果。
1 多变量过程监控模型
为更好地解决制造过程中出现的非线性过程和多模态过程的问题,本文提出了基于SOMM的过程质量状态建模与监控方法。先介绍了基于PCA的T2图和SPE图,以及基于SOM的最小量化误差(MQE)控制图,进而提出了基于SOMM的ED图和NLLP图。
1.1 基于主元分析的过程监控模型
主元分析主要通过线性空间变换求取主元变量,将高维数据空间投影到低维主元空间。因低维主元空间仍保留原数据空间的大部分方差信息,且主元变量间具有正交性,故可去除原数据空间的冗余信息。设过程变量数为m,采样次数为n,则过程数据矩阵X(nm)可分解为
(1)
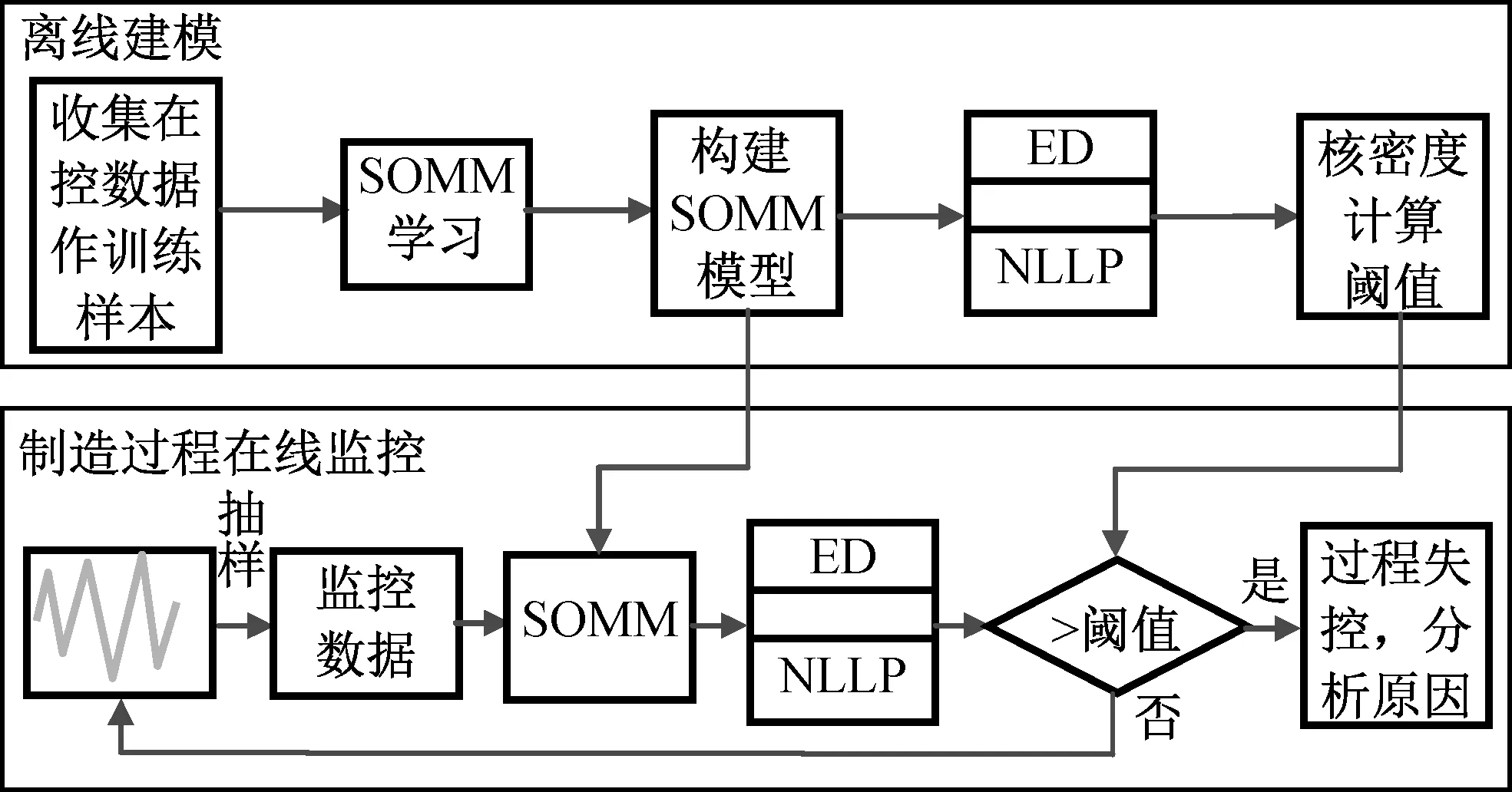
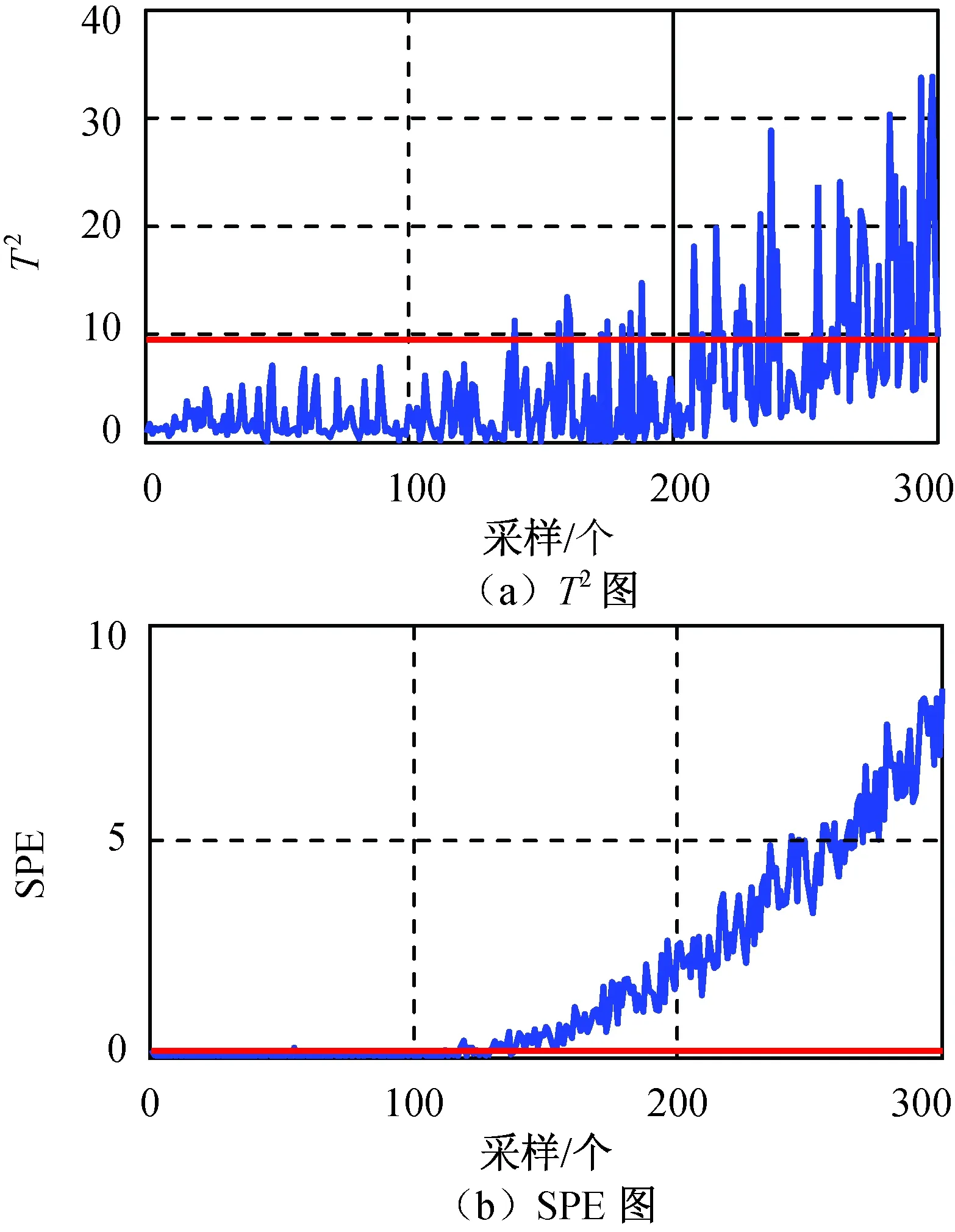
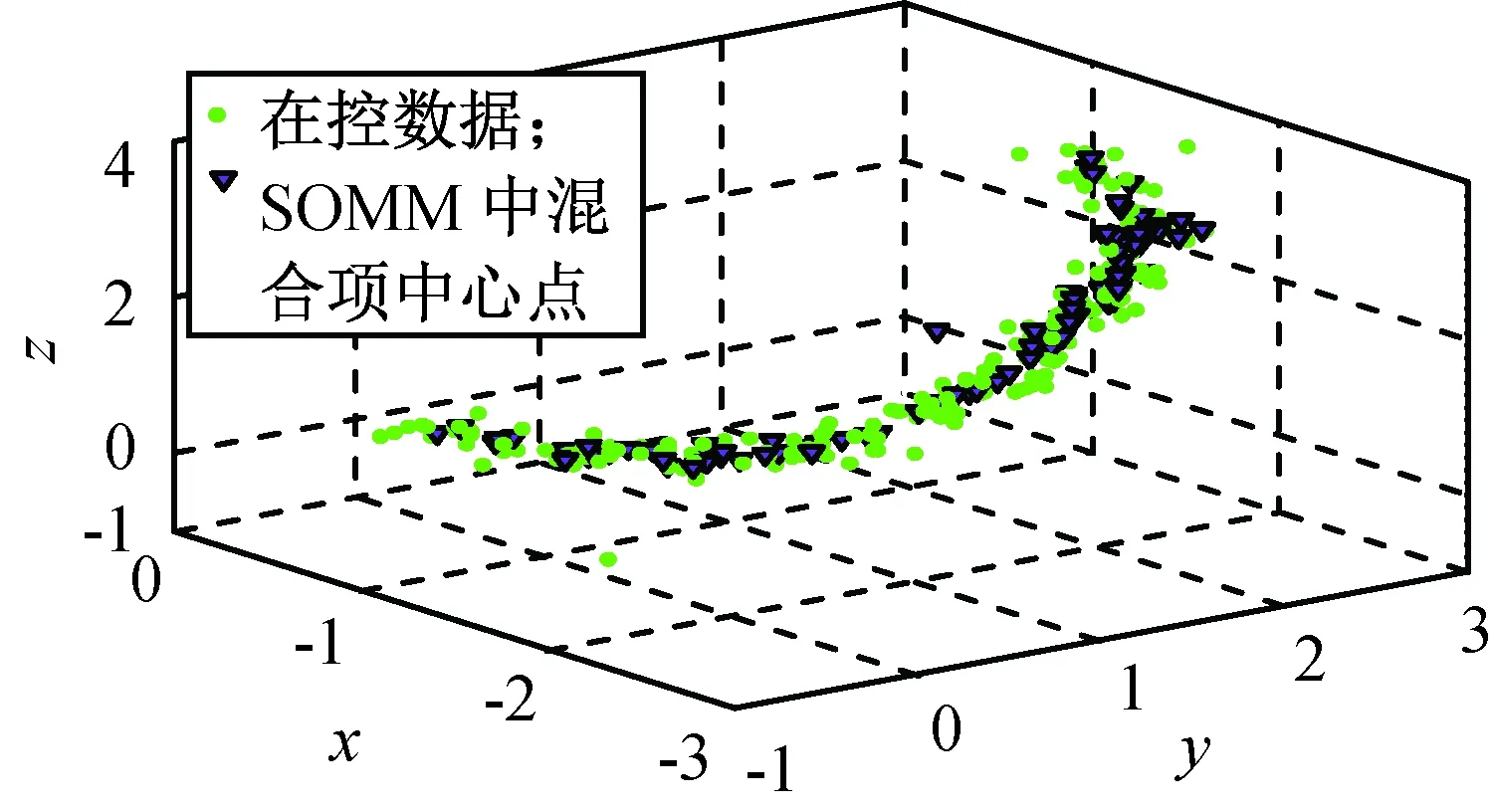
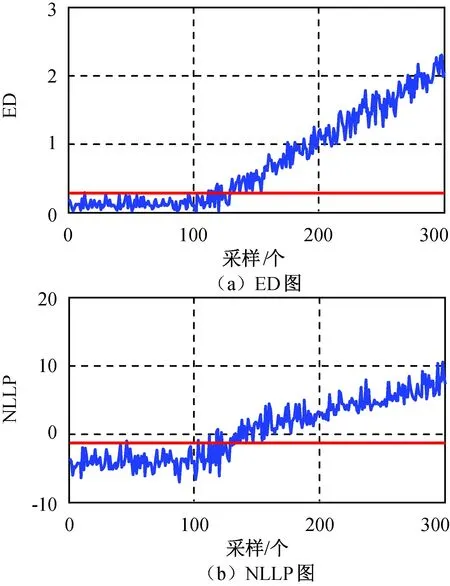
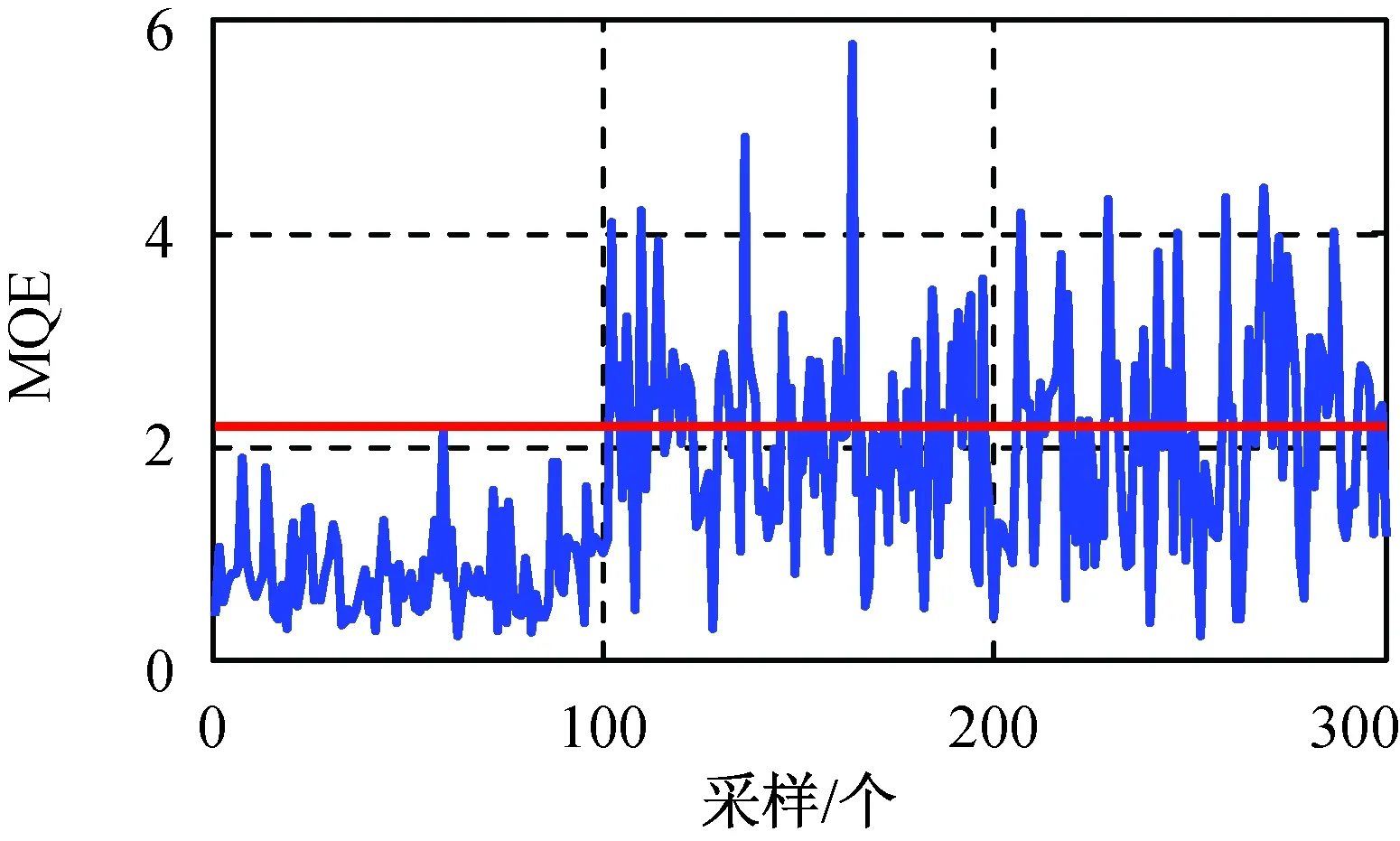
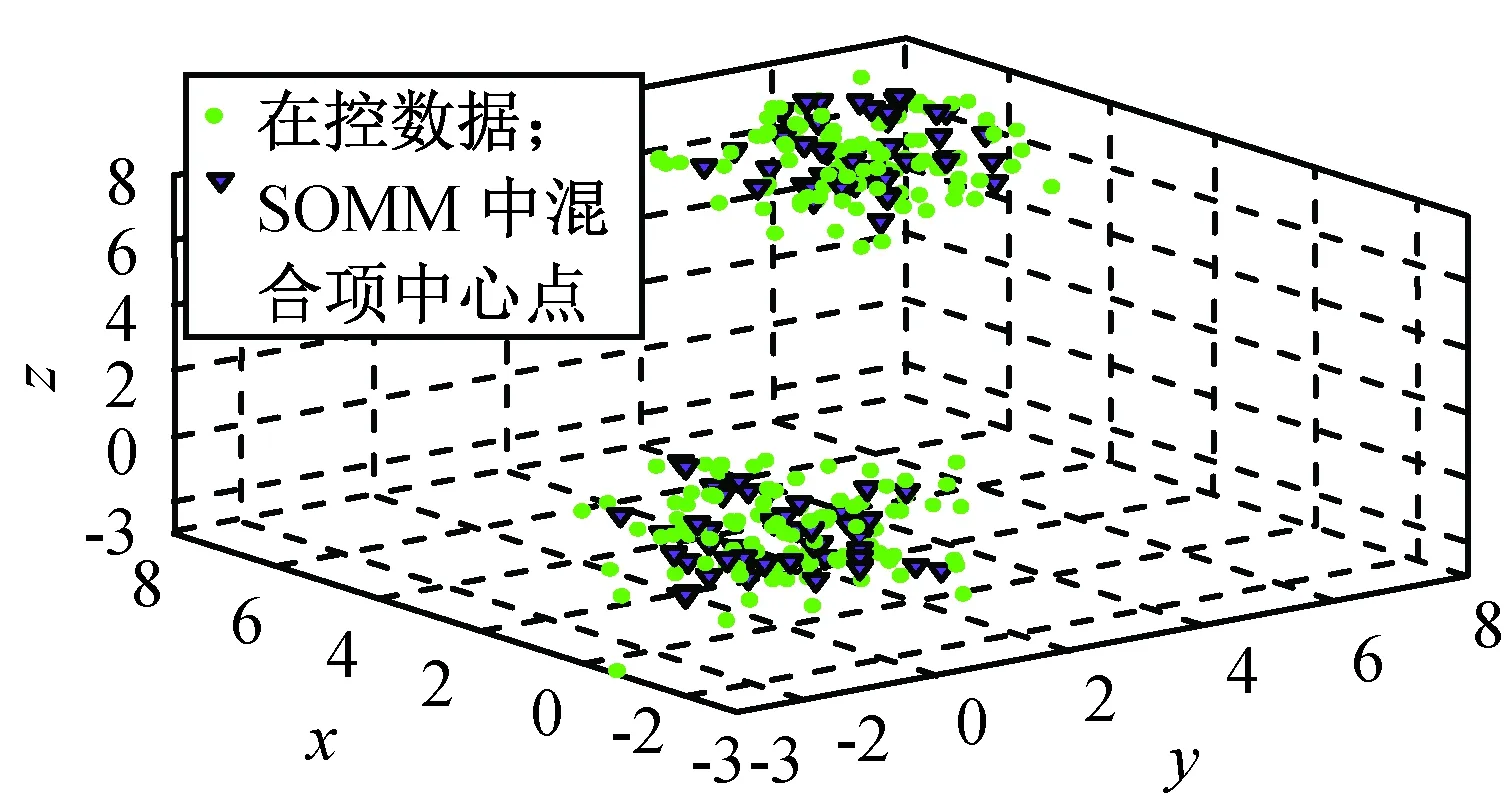
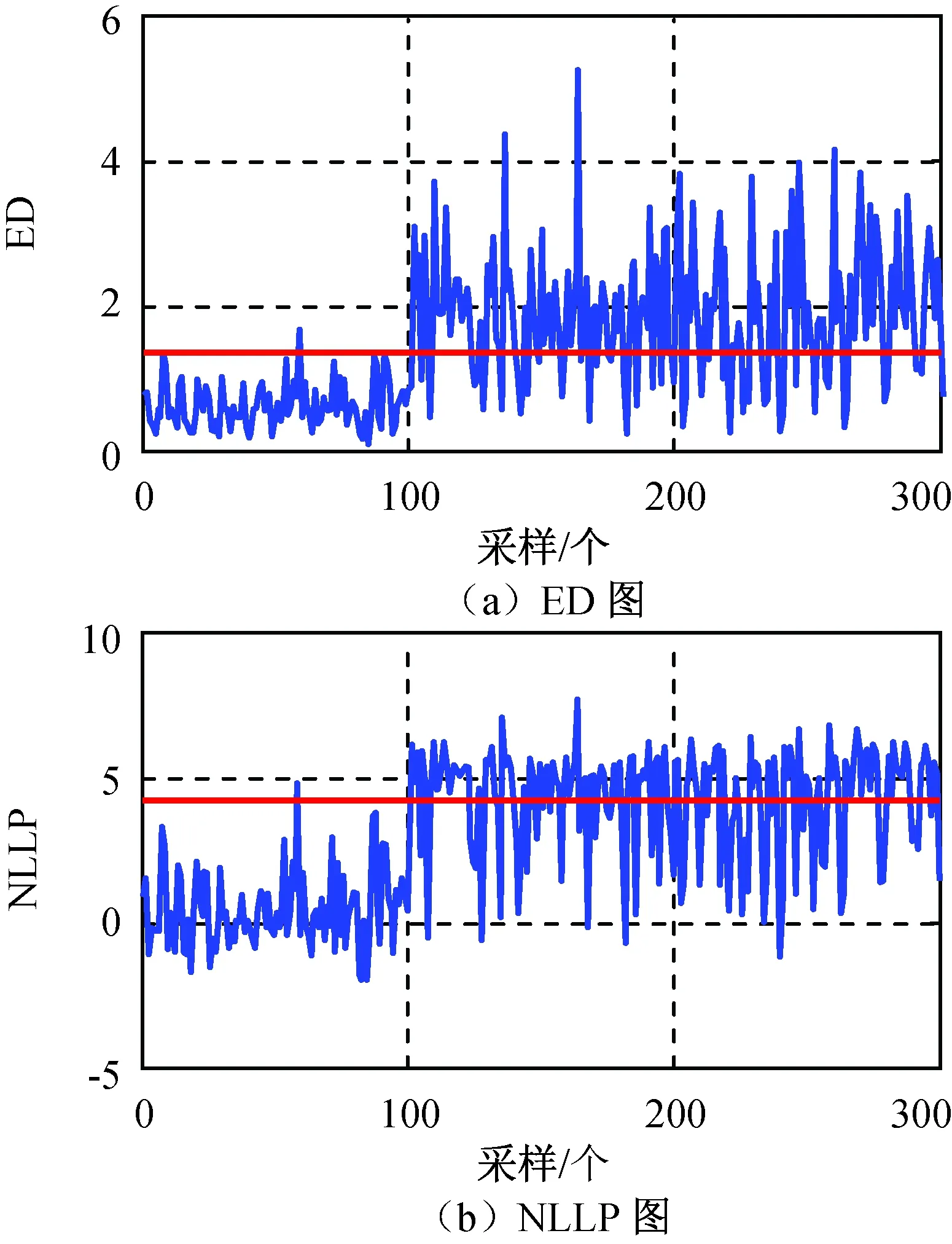
式中:pi为负荷向量;ti为得分向量。将ti按其长度从大到小排列,当X中的变量线性相关时,数据X的变化将主要体现在最前面的数个负荷向量上,用前k个主元(k 在多变量过程故障监控中,基于PCA的常用控制图主要有SPE和T2控制图,其定义分别为 δ(SPE)=eTe=(xi)T(1-PPT)xi; (2) T2=tTD-1t=(xi)TPD-1PTxi. (3) 式中:e为xi对应的残差向量;xi为第i时刻的过程向量;t为xi相应的得分向量;D为由与前k个主元对应的特征值组成的对角阵。由式(2)、(3)可知:SPE表述了测量值对主元模型的偏离程度,T2则代表了多变量过程的变化情况。 1.2 基于自组织混合模型的过程监控模型 1.2.1 自组织映射 SOM模拟了大脑神经系统自组织特征映射的功能,在训练中可无监督地进行自组织学习。SOM能将高维空间转为一维或二维空间表达,同时保持数据原有的拓扑逻辑关系。与主元分析等传统方法相比,SOM可对高度离散、非线性数据进行降维、建模等处理。 采用SOM模型监控生产过程时,首次采集一定量的在控数据,以创建和训练SOM模型,形成在控过程的数据特征空间模型。然后从制造过程在线采集观测向量,与SOM所有图元中的权值向量比较以获取最匹配单元(BMU),定义输入向量与BMU间的距离(MQE)为 δ(MQE)=‖D′-WBMU‖. (4) 式中:D′为输入向量;WBMU为BMU的权值向量[15]。MQE的大小表示了输入向量与正常状态空间的距离,因此可将其作为过程的监控指标。 1.2.2 自组织混合模型监控模型 SOMM综合了混合模型和自组织映射,故继承了两者的优点。与自组织映射相比,SOMM可嵌入更大型概率模型,在数据可视化和模式识别中有较好的效果。 设一个生产过程的高斯混合模型中各项有相等的混合权重,有 (5) (6) 引入N个隐含变量进行学习,每个隐含变量表示k个混合分量中的哪项生成了对应的数据点。EM算法将负对数似然值最大化 F(Q,θ)=EQlg p(s|x;θ)+H(Q)= (7) (8) a)E步:对每个输入xn,寻找分布qr*∈ϑ(ϑ为SOMM的高斯子),使F取得最大值,设qn=qr*。 1.2.3 制造过程状态量化指标 为判断一个新输入是否正常,本文提出两种基于SOMM的特征量化参数:用ED,NLLP与当前输入与正常状态的偏离程度进行比较,作为制造过程状态量化指标。 a)量化指标1:NLLP 对每个新的输入向量X,SOMM都将输出一个p(X),代表了该输入向量对SOMM模型表达的概率分布的符合程度。为改善监控效果,用其NLLP(见式(5))作为量化参数,其定义为 ). (9) 当观测向量来自在控过程,其NLLP等于或小于异常阈值;反之,当观测向量来自异常过程,其NLLP值会大于异常阈值。 b)量化指标2:最小ED 对一个新输入向量X,定义其与SOMM中第i个混合项的距离 di=(X-μi)(X-μi)T. (10) 式中:μi为第i个混合项的中心点;i=1,2,…,k。包含k个混合项的SOMM将计算得到一个响应向量集,则最小ED定义为 δ(ED)=min{d1,d2,…,dk}. (11) ED反映了当前输入X与在控状态空间的偏离程度。因此,通过跟踪时间轴上的ED变化,能实时监控过程状态。 1.2.4 信任限设置方法 对任何过程监控方案,需用信任限以判定过程是否失控。信任限的设置通常有两种方法:参数估计和非参数估计。当采用参数估计时,假定数据服从一种参数未知的分布,此时可根据样本估计未知参数值,然后根据该参数分布计算信任限;当采用非参数估计时,先根据观察值构建一个无参数估计,通过样本值计算概率密度,然后根据概率密度计算得到信任限。核密度估计是一种常用的无参数估计。设样本为X,长度为n,则其核估计可定义为 (12) 式中:h为带宽。K定义了概率密度分布的形状,h定义了其分布范围。采用核估计时通过累加概率密度即可得相应概率的信任限。本文用核密度估计计算信任限。 1.2.5 系统设计方案 基于SOMM的制造过程监控系统设计方案如图1所示。系统分成离线建模和在线监控两个部分。在离线建模阶段,通过在控数据建立SOMM模型和设置控制图的阈值;在在线监控阶段,对制造过程进行在线抽样,将采集数据输入已建立的SOMM模型,计算得到最小欧氏距离和负对数似然值,与阈值(即控制限)进行比较即可判断当前过程是否在控。 图1 SOMM模型在多变量制造过程中应用Fig.1 Application of SOMM model in multivariate manufacturing process 为验证基于SOMM的ED图和NLLP图在航天产品的非线性和多模态制造过程的监控性能,设计了两组实验:第一组仿真了一个3变量非线性制造过程;第二组仿真了一个3变量多模态制造过程。为与传统控制图比较,本文同时测试了基于PCA的T2图、SPE图和基于SOM的MQE图的性能。用平均运行步长(ARL)、异常探测率等性能指标比较ED图、NLLP图、T2图、SPE图和MQE图的制造过程监控性能。 2.1 实验参数设置 实验前,用户需提前设置模型的部分关键参数。设EM迭代步数1 000以获得SOMM的参数,最终的SOMM的对数似然值也需被记录以评估SOMM模型的学习效果。执行EM算法前,SOMM的参数(均值和方差)需被初始化,以获取更快的EM拟合,本文用K-Means算法初始化SOMM的参数。EM算法终止的标准为:完成1 000次迭代;当SOMM的对数似然值在连续的两个迭代步骤未被提高。通常在迭代过程中会满足第二个终止标准,这样EM一般无需进行1 000次迭代,学习效率被提高。 2.2 非线性制造过程 本实验模拟了一个3变量非线性制造过程,该过程有变量3个,但只有自变量1个,定义 (13) 式中:e1,e2,e3为相互独立的干扰变量,服从N(0,0,1)分布;a为[0,2]间的随机数。根据式(13)生成仿真数据作训练样本200组,另生成仿真数据作测试样本300组,从第101处起,在测试样本中的变量x1中加入一个d(t)=g*(t-100)的趋势型异常。此处:t为时间;g为趋势坡度值,g>0为上升趋势,g<0为下降趋势。取g=0.02σ,所得在控数据与测试数据分布如图2所示。 图2 非线性制造过程的在控数据与测试数据分布Fig.2 Distribution of in-control data and test data of nonlinear manufacturing process 先进行PCA分析,可知其前2个主元包含了所给数据99.35%的信息,因此实验中选择前2个主元作为输入,得到基于PCA的T2图和SPE图如图3所示。为便于比较,本实验中控制限置信概率统一定为0.99。由图3可知:当出现趋势型异常时,T2图和SPE图的指标均随时间推移而逐渐上升,但效果相差很大,T2图在第160处才监测到异常,SPE图则远优于T2图,在第120处发现异常,但异常探测灵敏度有待进一步提高。 图3 非线性制造过程基于PCA的T2图和SPE图Fig.3 T2 and SPE graph of nonlinear manufacturing process based on PCA 用SOM进行分析,得到MQE图如图4所示,其置信概率为0.99。由图4可知:在约135处监测到异常发生,灵敏度优于T2图,但不及SPE图。 图4 非线性制造过程基于SOM的MQE图Fig.4 MQE graph of nonlinear manufacturing process based on SOM 根据在控数据建立SOMM如图5所示。由图5可知:模型充分描述了在控数据。SOMM建立后,将测试数据输入其中,所得ED,NLLP图如图6所示。由图6可知:当出现异常时,其ED,NLLP快速上升,在120处越过控制限,灵敏度优于T2图和MQE图,与SPE图相当。 图5 非线性制造过程SOMM建模Fig.5 SOMM modeling of nonlinear manufacturing process 图6 非线性制造过程基于SOMM的ED图和NLLP图Fig.6 ED and NLLP graph of nonlinear manufacturing process based on SOMM 2.3 多模态制造过程 在生产过程中,系统可能存在不同的稳定工作状态,本实验模拟了一个2模态3变量过程。定义变量 (14) 式中:si1,si2均服从高斯分布;i=1,2,3。状态Ⅰ总体均值向量μ1,Σ1分别为 μ1=[0 0 0]T, 状态Ⅱ总体均值向量μ2,Σ2分别为 μ2=[6 6 6]T, 状态Ⅰ、Ⅱ均为正常在控状态,分别仿真产生数据100组作为在控数据,另根据状态Ⅰ仿真生成数据300组作为测试样本,从101处起,在测试样本中s11加上一个大小为3σ的阶跃型异常,数据分布如图7所示。 图7 多模态制造过程在控数据与测试数据分布图Fig.7 Distribution of in-control data and test data of multi-mode manufacturing process 先进行传统PCA分析,通过分析选取前2个主元,所得基于PCA的T2图和SPE图如图8所示。为便于比较,本实验中置信概率统一定为0.99。由图8可知:T2图探测率非常低,监控效果很差;SPE图监控效果较好,但探测率仍较低。 图8 多模态制造过程基于PCA的T2图和SPE图Fig.8 T2 and SPE graph of multi-mode manufacturing process based on PCA 用SOM进行分析,所得MQE图如图9所示,其置信概率为0.99。由图9可知:MQE图可快速检测到异常,探测率较SPE图有所提高,但仍不很理想。 图9 多模态制造过程基于SOM的MQE图Fig.9 MQE graph of multi-mode manufacturing process based on SOM 根据在控数据建立SOMM如图10所示。由图10可知:模型充分描述了在控数据。SOMM建立后,将测试数据输入该模型,所得ED图和NLLP图如图11所示。由图11可知:当过程出现异常时, ED,NLLP快速上升,可快速检测到异常,探测率较MQE图进一步提高。 图10 多模态制造过程SOMM建模Fig.10 SOMM modeling of multi-mode manufacturing process 图11 多模态制造过程基于SOMM的 ED图和NLLP图Fig.11 ED and NLLP graph of multi-mode manufacturing process based on SOMM 由于传统的多变量统计过程控制方法对航天器的各类部件(主要关键铝合金部件)加工过程的多变量制造过程(呈现多模态、非线性分布)无法实现有效的控制,本文提出了基于SOMM的过程控制方法,并开发了ED,NLLP过程状态量化指标,进一步应用于多变量过程的监控,实验表明这两种控制图在非线性及多模态过程中具有良好的监控效果。为验证该模型的效果,将之与PCA和SOM模型在非线性和多模态过程的监控效果进行比较,分析结果表明:与其他控制图相比,ED,NLLP控制图在平均运行步长和异常探测率方面均有更好性能。基于SOMM的ED,NLLP控制图的提出,对非线性和多模态制造过程的质量控制提供了一种有效的解决途径。基于SOMM的ED,NLLP控制图可用于现代航天器的各类部件(如铝合金部件)的工序加工过程质量的控制,后续可对其在实际工程应用中的有效性进行验证,进一步研究基于SOMM的ED,NLLP控制图的多变量制造过程故障源诊断,以实现对失控过程的快速调整。 [1] 范蕾懿. 质量安全与质量风险管理研究[J]. 上海航天, 2014, 31(S1): 35-37+59. [2] SPANOS C J. Statistical process control in semiconductor manufacturing[J]. Proc IEEE, 1992, 80(6): 819-830. [3] JACKSON J E. A user’s guide to principal components[M]. New York: Wiley, 1991. [4] DONG D, MCAVOY T J. Nonlinear principal component analysis based on principal curves and neural networks[J]. Computers & Chemical Engineering, 1996, 20(1): 65-78. [5] LEE J M, YOO C K, LEE I B. Statistical process monitoring with independent component analysis[J]. Journal of Process Control, 2004, 14: 467-485. [6] LEE J M, QIN S J, LEE I B. Fault detection and diagnosis based on modified independent component analysis[J]. AIChE Journal, 2006, 52: 3501-3514. [7] HU K, YUAN J. Multivariate statistical process control based on multiway locality preserving projections[J]. Journal of Process Control, 2008, 18: 797-807. [8] ARADHYE H B, BAKSHI B R, DAVIS J F, et al. Clustering in wavelet domain: a multiresolution ART network for anomaly detection[J]. AIChE Journal, 2004, 50(10): 2455-2466. [9] GUH R S. On-line identification and quantification of means shifts in bivariate processes using a neural network-based approach[J]. Quality and Reliability Engineering International, 2007, 23(3): 367-385. [10] 朱波, 刘飞, 李顺江. 基于优化有向无环图支持向量机的多变量过程均值异常识别[J]. 计算机集成制造系统, 2013, 19(3): 559-568. [11] YU J B. Hidden Markov models combining local and global information for nonlinear and multimodal process monitoring[J]. Journal of Process Control, 2010, 20: 344-359. [12] SALEHI M, BAHREININEJAD A, NAKHAI I. On-line analysis of out-of-control signals in multivariate manufacturing processes using a hybrid learning-based model[J]. Neuro Computing, 2011, 74(12/13): 2083-2094. [13] YU J B. Fault detection using principal components-based Gaussian mixture model for semiconductor manufacturing process[J]. IEEE Transaction on Semiconductor Manufacturing, 2011, 24(3): 432-444. [14] 罗先喜, 苑明哲, 王宏. 基于主元分析确定多变量系统控制极限的方法[J]. 计算机集成制造系统, 2012, 18(10): 2331-2336. [15] YU J B, XI F. Using an MQE chart based on a self-organizing map NN to monitor out-of-control signals in manufacturing processes[J]. International Journal of Production Research, 2008, 46(21): 5907-5933. Multivariable Manufacturing Process Control for Aerospace Product Based on Self-Organizing Mixture Model YU Jian-bo1, LI Chuan-feng1, WU Hao2, CHENG Hui3 (1. School of Mechanical Engineering, Tongji University, Shanghai 201804, China; 2. Shandong Special Equipment Inspection Institute, Jinan 250101, Shandong, China; 3. Shanghai Aerospace Equipments Manufacturer, Shanghai 200245, China) To solve effective monitoring difficulties in process control when using conventional multivariate process control methods because of nonlinear or multimodal characteristics shown in some complicated multi-variable manufacturing processes for aerospace products due to the randomness of the manufacturing process, a process control method based on self-organizing mixture model (SOMM) was proposed to implement the modeling and monitoring of nonlinear and multimodal processes in this paper. Self-organizing map and mixture model were combined in this method to accomplish the modeling of the nonlinear and multimodal processes. The threshold value of the control chart was set. The two control charts were proposed to identify and assess the process states online, which were the minimum Euclidean distance chart and the negative log-likelihood probability chart. The proposed manufacturing process control system based on SOMM was composed of two parts which were modeling out line and control on line. To verify the monitoring performances of this method in nonlinear and multi-modal processes, two simulation experiments were conducted, and then comparison was performed with traditional methods such as principal component analysis and self-organizing map. The experimental results show that the proposed method has better monitoring performances than the regular method in nonlinear and multi-modal processes and it can apply to the quality control of the aerospace products manufacturing. Multivariable manufacturing process; Process quality; Statistical process control; Process control; Control chart; Multimodal; Nonlinear; Self-organizing mixture model 1006-1630(2016)05-0042-08 2016-06-27; 2016-09-04 国家自然科学基金资助(51375290);中央高校基本科研业务费 余建波(1978—),男,博士,副教授,主要研究方向为数据挖掘、智能维护和机器学习。 TP277; V461 A 10.19328/j.cnki.1006-1630.2016.05.007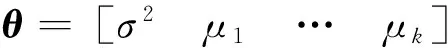
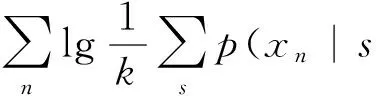

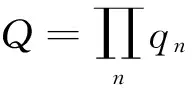

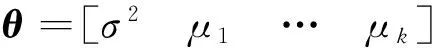

2 实验分析



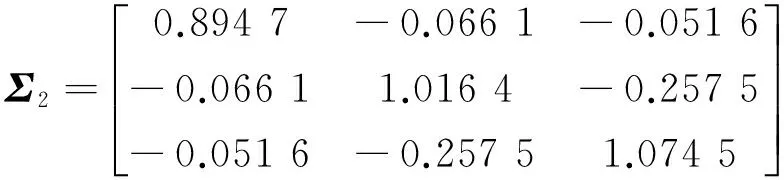


3 结束语
