整体思想在高中数学解题中的应用实践探讨

林津伊

摘 要：学生在学习数学时，要掌握数学解题思路与方法，能够做到触类旁通，而非死记硬背。在实际学习中，要不断总结各种数学解题思路，对于书本中的知识可以进行深入的理解与掌握。整体思想在中学数学学习中有着非常重要的作用，如果能够从整体出发，找到数学解题捷径，必然会达到事半功倍的效果，提高学习效率。本文主要分析了整体思想在高中数学解题中的应用，通过总结作者自身在高中数学学习中的整体思想运用经验，以期能够为其他学生提供一些参考借鉴。

关键词：整体思想；高中数学；解题；学生

整体思想是指从整体出发来研究问题，将问题中的不同部分细化成不同的整体，以此来提高数学解题效率。当在数学解题中运用整体思想时，我们应分析问题的整体特征，把一些图形以及式子都视作整体，并且研究不同整体间的关系，从而有目的、有针对性地对高中数学题进行整体处理。

一、学生要注意培养自身的数学学习兴趣

在学习数学时，学生要强化自身对数学的学习兴趣。在数学课堂上，当老师提出一个带有悬念的问题时，学生要积极地进行响应，分析问题所具有的各种答案，通过自身努力探索，勤于思考，在课下查阅资料或者向老师请教，从而找到问题的答案，以此来培养良好的数学学习兴趣。例如，在学习椭圆方程时，学生可以在课前查阅资料，利用几何画板等软件，了解椭圆曲线以及相应的方程，并且了解方程中的常数是怎么得出的，注重椭圆曲线的整体性。这样当老师在课堂上进行讲解时，学生就能够更加容易听懂，从而增强自信心，提高对于数学的学习兴趣，而不会对高中数学产生畏惧感。

二、学生要树立整体思想，有条不紊地进行学习

当学生有很好的数学学习兴趣以后，就要注重树立整体思想，并自主探索数学中所包含的各种规律。也就是说老师给学生提供整体思想框架，接下来学生自己要多去探寻框架内的各个知识点，从整体到局部，有计划地掌握数学知识。

例如，在学习数学集合这一节时，当老师为学生讲解集合方面的概念以后，学生就要主动了解集合的性质，分析并集、交集、子集所指的范围，归纳总结出集合所具有的确定性、互异性等性质，从而为基于集合知识的其他题目解答打下基础。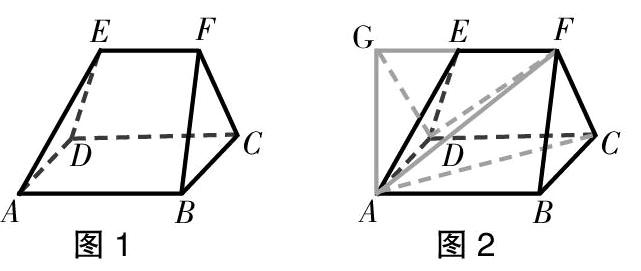

当树立整体思想以后，学生在解决具体数学问题时，就可以先找到问题的主线，分析主线上面的各个支干问题，对各种烦琐的数学问题加以处理。例如，在学习立体几何这一章内容时，当看到题目时，我们可能一开始会感觉束手无策，不知从何下手，但是当具备整体思想，了解立体几何的主线证明与计算以后，就可以很从容地解题了。我们先要根据题干中的已知条件证明所要得到的结论，先处理线与线的关系，再处理线与面、面与面关系。接着要进行计算，从角与距离这两条主线出发。关于角的计算包括线与线、线与面、面与面所组成的角的计算；关于距离的计算主要有点到点、点到线、点到面以及线到线、线到面的距离的计算，最后要处理面到面的距离。在这些问题处理过程中，我们要能够始终把握住主线，从整体出发，由整体到局部，有条不紊地解决各种问题。当所有的小问题得以解决之后，大问题也就解决了。

三、要注重构建数学整体，而非纠结于单一元素

在学习中，“温故而知新”是一种非常有效的学习方法，能够让学生在掌握旧知识的基础上学到新知识。对于高中数学学习也是如此，我们通过对旧知识进行总结、整理以及运用，从而达到解决新问题的目的。这一学习方法在高中代数学习中运用效果最为显著。当我们学习代数知识时，会遇到很多第一眼看起来好像已知条件不够无法求解的题目，但其实如果运用整体思想对这一类型的题目加以求解，就会很容易得到答案。这就需要我们平时有意识地构建起整体思想，而不能过于纠结某一个方面。在代数中有很多定理，这些定理在我们学习之后就成为潜在的已知条件了，因此在解决新的代数问题时学生可以运用这些定理。可以说我们对于旧知识运用的熟练程度，会在很大程度上决定我们处理新问题的效率。如关于三角函数的数学求解问题，一般角度的三角函数值我们学生都知道，如30°、45°、60°、90°等，但如果是不经常用到的角度如25°，这样我们就无法直接得出它的三角函数值，但如果学生过于纠结直接得出25°的三角函数值，就会陷入困境中。这时就需要我们能够从整个题目求解出发，运用所学的三角函数转换定理，将不常见的角度转换为常见的角度进行求解。这样我们不但可以简化数学问题，同时还能够温习所学过的知识，达到很好的学习效果，同时也为以后学习新的知识打下了扎实的基础。下面通过一个例子来对这一点进行更加充分的说明。

如果我们仅仅注重题目中的某一元素，那么这一题目必然无法顺利求解出来。因此可以看出不论是代数问题，或者是其他数学问题，我们都应该具有整体思想，当需要的时候能够及时搬出来加以运用，能够起到意想不到的效果。

四、适当添加，构造整体

整体构造，主要是按照已知条件以及所要求解的结果，对原来式子或已知条件进行补充，构建出一个整体再加以求解。很多试题一眼看上去感觉试题不够完整，无从下手，而如果运用整体构造方法，就能便捷迅速地得到答案。主要的着手点就是从局部出发拓展成一个整体，通过研究整体来解决局部问题。

从中可以看出巧妙运用整体思想，将部分补充为整体，会极大地简化解题过程，起到巧妙解题的效果。我们学生通过运用这一方法，不但能培养自身的解题能力，同时也能提高解题效率，有利于学习兴趣的强化。

五、整体换元，将复杂问题简单化

整体换元法也是整体思想中非常重要的一部分。它主要是指在试题求解过程中，对一个整体进行换元，从而引入新的元，把原先很复杂的公式转变为比较简单的式子，简化求解过程，使得学生能够理清解题思路，进行快速求解。

六、要注重班级或者小组这个整体，加强团队合作

在学习过程中要注重班级或者小组这个整体，相互交流学习思路、学习方法，当遇到难以求解的题目或者难点时，学生整体间可通过沟通、交流来解决，这样远远比一个人冥思苦想效率要高得多，而且大家一起思考，共同探索，有时候还可以找到新的解题思路，拓展视野。在小组内，同学间可以自由讨论，从而加快试题解决过程。通过小组讨论，还能够让不同学生互相取长补短，认识到自身的不足，缩短与他人的距离。注重班级这个整体，会增强学生对于班集体的荣誉感、归属感，从而使之愿意为班集体建设作出更多贡献，发挥团队精神，这样对我们以后的学习、工作都是非常有帮助的。

总而言之，在高中数学学习中，注重整体思想，合理利用整体解题思路能够有效激发学生对高中数学的学习兴趣，提高高中数学解题能力，从而在考试中缩短解题时间，取得更加优异的成绩。运用整体思路要求学生能够做到从整体出发，顾全大局，当遇到难解的试题时，可以找到主线，从而继续延伸下去，分析各个细节部分，由整体到局部，细化题干内容。增强对高中数学基础知识的掌握程度，具备运用旧知识处理新问题的能力，对于数学定理、公式能够随时记起并且当运用整体思想时能够灵活运用，要经常梳理基础知识，进行归纳总结，完善数学知识体系，查漏补缺，真正提高数学学习水平。

参考文献：

[1]董诗林.化归转化思想方法在高中数学中的应用实践[J].上海中学数学，2016（4）：40-42.

[2]蔡小雄.更高更妙的高中数学思想与方法（第七版）[M].杭州：浙江大学出版社，2015.