作为动直线运动轨迹的二次曲面

黄保军

（淮北师范大学 数学科学学院，安徽 淮北 235000）

作为动直线运动轨迹的二次曲面

黄保军①

（淮北师范大学 数学科学学院，安徽 淮北 235000）

二次曲面是空间解析几何最重要的内容之一.研究二次曲面，除利用平行截割法，通过综合分析截痕的变化来认识曲面的形状外，还可通过分析曲面的内部结构来把握其几何特征.文章基于单叶双曲面和双曲抛物面的直母线性质，详细论证了这2类曲面均是遵循一定规律的动直线的运动轨迹，从而直观揭示它们的几何特征，为利用几何法定义这些曲面奠定可靠的理论基础.

单叶双曲面；双曲抛物面；直母线

0 引言

所谓二次曲面，是指在空间直角坐标系下，由三元二次方程

所表示的图形.通过坐标变换可知，非退化实二次曲面共有9种：椭球面，2种双曲面，2种抛物面，二次锥面和3种二次柱面［1］.这些二次曲面中，二次锥面和二次柱面，显然分别是共点直线族和平行直线族的轨迹；而椭球面、双叶双曲面和椭圆抛物面上均没有直线［1］，所以，它们不可能是动直线运动而形成的轨迹；至于单叶双曲面和双曲抛物面，一般教科书上仅就其直纹性和直母线族的性质作了简单探讨，多数教科书对它们的直母线的性质没做证明（如文献［2-3］等）.受这2种曲面直母线性质的启发，文献［4］通过实例验证单叶双曲面和双曲抛物面，都可看成动直线运动而形成的轨迹；文献［5］则在理论依据不够充分的情况下，笼统地将单叶双曲面定义为与3条互相异面的直线都共面的动直线所生成的曲面，而将双曲抛物面定义为与2条异面直线都相交且平行于定平面的动直线所产生的曲面.本文一方面将文献［4］中实例的结果向一般化推广，同时也将纠正文献［5］中所给出的单叶双曲面和双曲抛物面定义的理论和逻辑上的错误.

1 单叶双曲面作为动直线运动的轨迹

定理1 设L1,L2,L3为3条两两异面的直线，且3条直线不平行于同一平面，则与3条异面直线均共面的动直线的轨迹是一单叶双曲面.

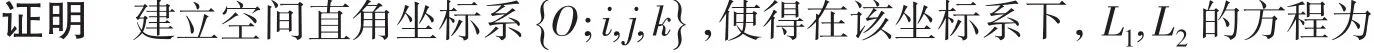
定义1 设L1,L2,L3为3条两两异面的直线，且这3条直线不平行于同一平面，称与L1,L2,L3均共面的动直线的轨迹为单叶双曲面.

2 双曲抛物面作为动直线运动的轨迹

定理2 设L1,L2,L3为3条两两异面直线，且这3条直线平行于同一平面，则与3条异面直线均共面的动直线的轨迹是一双曲抛物面.

注1 定理2推广了［4］中的例4.

定理3 设L1,L2为2条异面直线，π0为一定平面，L1,L2均不平行于π0，则与L1,L2均共面且平行于π0的动直线的轨迹是一双曲抛物面.

注2 定理3推广了［4］中的例6.

注3 若2条异面直线L1,L2有一与定平面π0平行，则与L1,L2均共面且平行于定平面π0的动直线的轨迹是二相交平面；若2条异面直线L1,L2均与定平面π0平行，则与L1,L2均共面且平行于定平面π0的动直线的轨迹是二平行于π0的平面.

由定理2和定理3，可给出如下的2个定义:

定义2 设L1,L2,L3为3条两两异面直线，且这3条直线平行于同一平面，称与L1,L2,L3均共面的动直线的轨迹为双曲抛物面.

定义3 设L1,L2是与定平面π0相交的2条异面直线，称与L1,L2均共面且平行于定平面π0的动直线的轨迹为双曲抛物面.

注4 对一种事物或一个概念下定义，即对这种事物的本质特征或这个概念的内涵和外延作简要说明.结合定理1—3，不难发现，本文关于单叶双曲面和双曲抛物面的定义，较文献［5］更为严密、准确，更切合定义的基本要求.

［1］杨文茂.解析几何习题选集［M］.武汉：武汉大学出版社，1983:8.

［2］郑崇友，王汇淳，侯忠义，等.几何学引论［M］.2版.北京：高等教育出版社，2005:8.

［3］吕林根，许子道.解析几何［M］.4版.北京：高等教育出版社，2005:8.

［4］刘绍颖.直纹面可视为动直线的轨迹［J］.承德民族师专学报，1995（2）：24-27.

［5］陈怀堂，杜彦武，刘建.关于单叶双曲面和双曲抛物面的定义［J］.临沂师专学报，1997，19（3）：1-3.

Quadratic Surfaces Defined as Locus of Rectilinear Motion

HUANG Baojun
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

Quadratic surfaces are important in solid analytic geometry.The shape of surfaces can be under⁃stood by using parallel section method and analyzing change of the sections.Geometric characteristics can al⁃so be understood by discussing internal structure of the surfaces.Based on the properties of the ruling of the surfaces，we concluded that hyperboloid of one sheet and hyperbolic paraboloid are loci of rectilinear motion complying with some rules，which reveal their geometric characteristics.These results would be a theoretical foundation on defining the surfaces with the use of geometric method.

hyperboloid of one sheet；hyperbolic paraboloid；ruling

O 182.2

A

2095-0691（2016）04-0004-04

2016-06-21

安徽省高校省级教学质量与教学改革工程项目（2012gxk191）

黄保军（1957- ），男，安徽砀山人，教授，研究方向：几何与拓扑.