基于变换域的局部最优纯方位航迹关联*
2016-12-20崔雨勇
崔雨勇
(中国西南电子技术研究所,成都 610036)
基于变换域的局部最优纯方位航迹关联*
崔雨勇**
(中国西南电子技术研究所,成都 610036)
针对同平台无源传感器纯方位线关联问题,提出了一种基于变换域的局部最优航迹关联算法。该算法采用霍夫变换(Hough Transform)将方位线映射到参数域等价为点描述,将不同方位线的点描述构建成时间的离散函数,利用时间对准形成具有相同时标的点序列。对关联门限内的目标构建指数判证函数,计算满足关联门限目标的关联矩阵,并确定各航迹关联程度,采用局部寻优方法求取最优关联度的目标作为关联对。实验表明,所提算法具有较好的稳定性及时效性,有效解决了同平台多方位线关联问题。
无源探测;航迹关联;局部最优;霍夫变换;纯方位线
1 引 言
随着探测技术的快速发展,现代战场获取的信息手段越来越多,使得处理变得越来越复杂。为了获取最有效的探测,单传感器探测已经无法满足战场作战指挥需求,因此必须使用多传感器进行探测并完成实时处理,形成统一态势[1]。当前,为了能够更有效发现敌人,无源探测技术如通信侦察、光电侦察等被引入使用。相对于有源探测而言,无源探测具有不易被敌人察觉、探测距离远等优点。
无源探测获取的目标信息很多情况下只有方位信息。雷达在敌方干扰情况下,获取的目标信息也可能仅有方位信息。航迹关联[2-3]是多传感器探测系统的关键技术之一,其关联的准确性对系统航迹生成具有重要的影响。纯方位航迹关联的难度更大。针对纯方位航迹关联问题,文献[4]提出了一种以航迹异同性和关联程度,进行总体位移差、总体一阶斜率差及二阶差,采用B型灰色相关方法(下文称为B方法)完成航迹相关。在测量误差增大时,其总体一阶斜率差与二阶斜率差波动增大,导致正确关联率下降。文献[5]提出将方位信息映射到单位圆坐标上进行Hausdorff距离计算,描述航迹的几何形状相似度,并结合灰度关联思想进行航迹关联。该算法(下文称H方法)随着目标个数的增加,其方向距离描述能力不能满足目标多的情况。文献[6]提出了一种基于期望检验和方差检验方法(下文称P方法),算法表现较前两者有效,但是其仍然需要对所有数据进行计算。该算法不能满足快速关联及目标先验概率未知的情况。
本文提出一种局部关联策略,采用变换域关联达到方位关联的目的。实验表明该算法在相同情况下比上述算法具有更好的稳定性。
2 纯方位航迹问题
2.1 问题描述
设同一平台具有两部无源传感器,由于无源探测获取的是目标方位信息,其航迹表现为不同时刻探测到的目标方位航迹信息。为了说明问题,作如下假设:
(1)无源探测传感器1、2的航迹号集合分别为
U1={1,2,3,…,n},U2={1,2,3,…,n}。
(1)
设
(2)
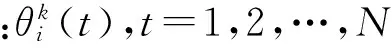
(2)假设传感器探测信息独立,同一传感器的不同航迹是互不关联的;
(3)无源关联问题可以等价于如下问题:
H0传感器1的第i条航迹与传感器2的第j条航迹是同一目标的航迹信息;
H1传感器1的第i条航迹与传感器2的第j条航迹不是同一目标的航迹信息。
这样,纯方位关联问题就可以转换为假设检验问题。
在本文中,假设传感1与传感器2的航迹间不存在明显不相关问题,即航迹相关性是相同的。
2.2 霍夫变换
霍夫变换(Hough Transform)是图像处理为了获取目标边缘、角点特征等信息所采用的一种变换域检测法,其基本思想是点-线对偶关系。具体原理描述如下:
y=ax+b。
(3)
式中:a为直线斜率;b为截距。将式(3)变形,可得到
b=-ax+y,
(4)
则(b,-a)为一组参数空间的点,直线为过该点的一条直线,如图1所示。
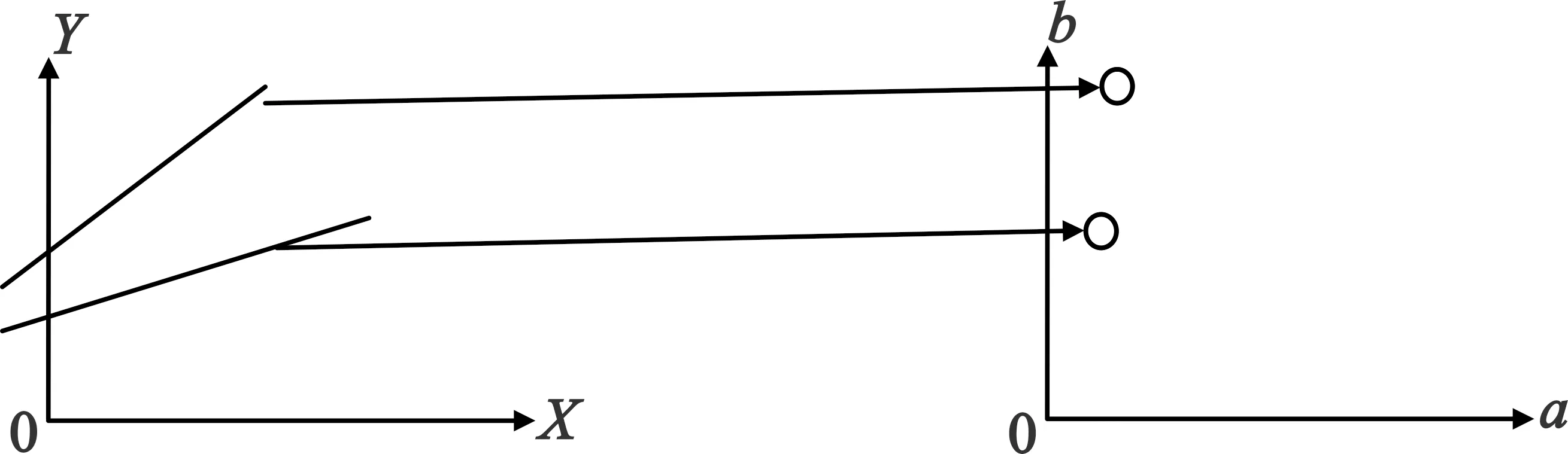
图1 霍夫变换示意图
Fig.1 Schematic diagram of Hough Transform
在传感器探测中,由于b始终为0,则可以将传感器探测角度定义为一组(t,a)曲线,其中t表示采样时间点,则可以进行有效的关联。
3 纯方位航迹关联算法
3.1 时间对准问题
解决纯方位多传感器的时间对准问题时,通常采用匀角速度变换率插值法进行。设无源传感器在ti与ti+1时刻获得的方位角分别为θ(ti)与θ(ti+1),则目标在t时刻的方位角θ(t)为
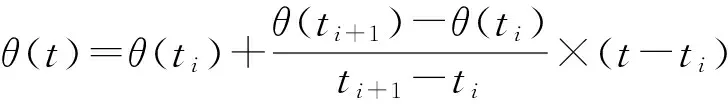
(5)
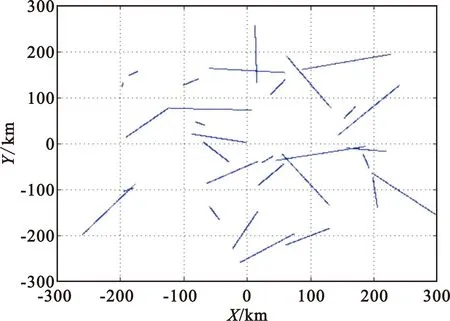
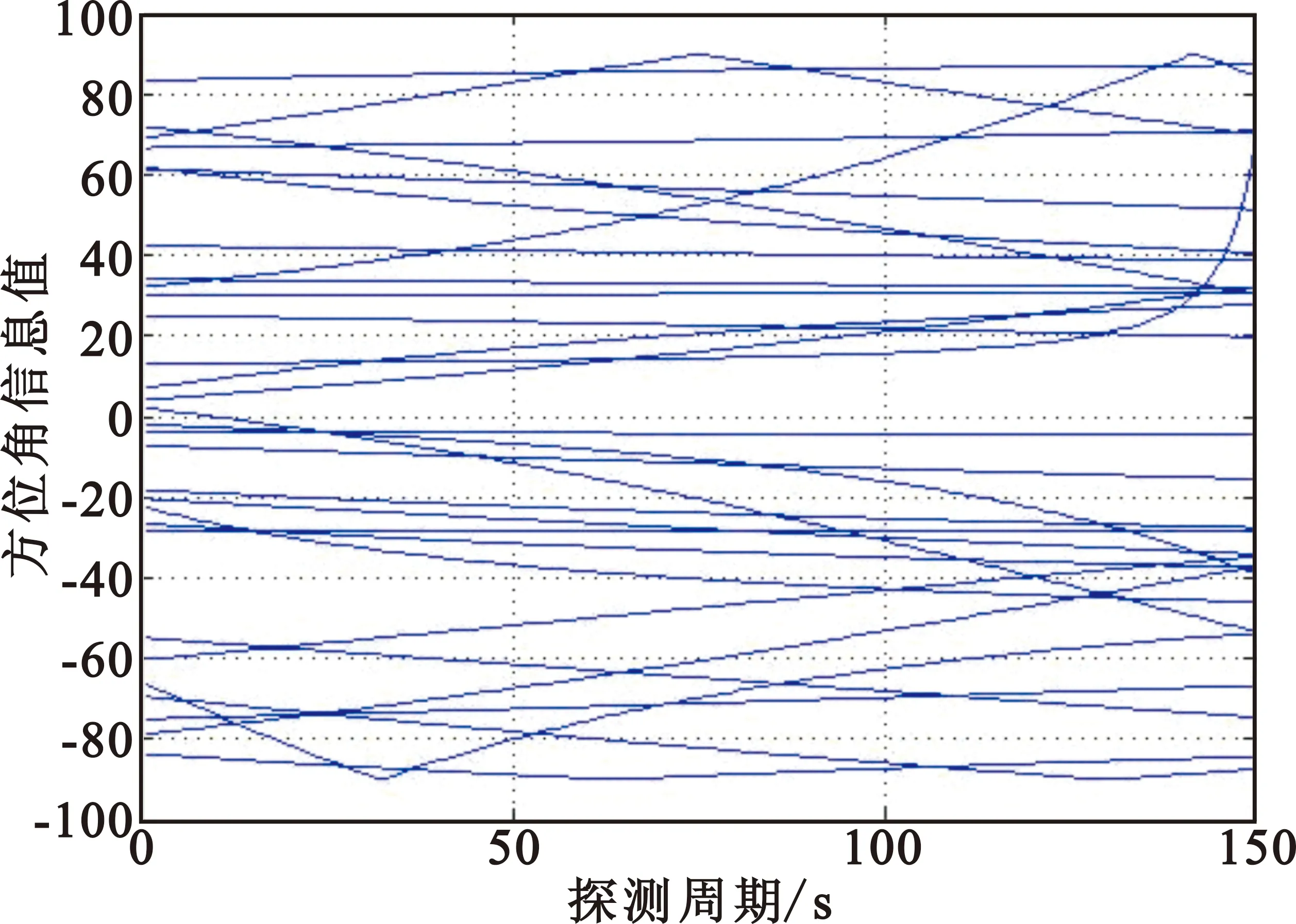
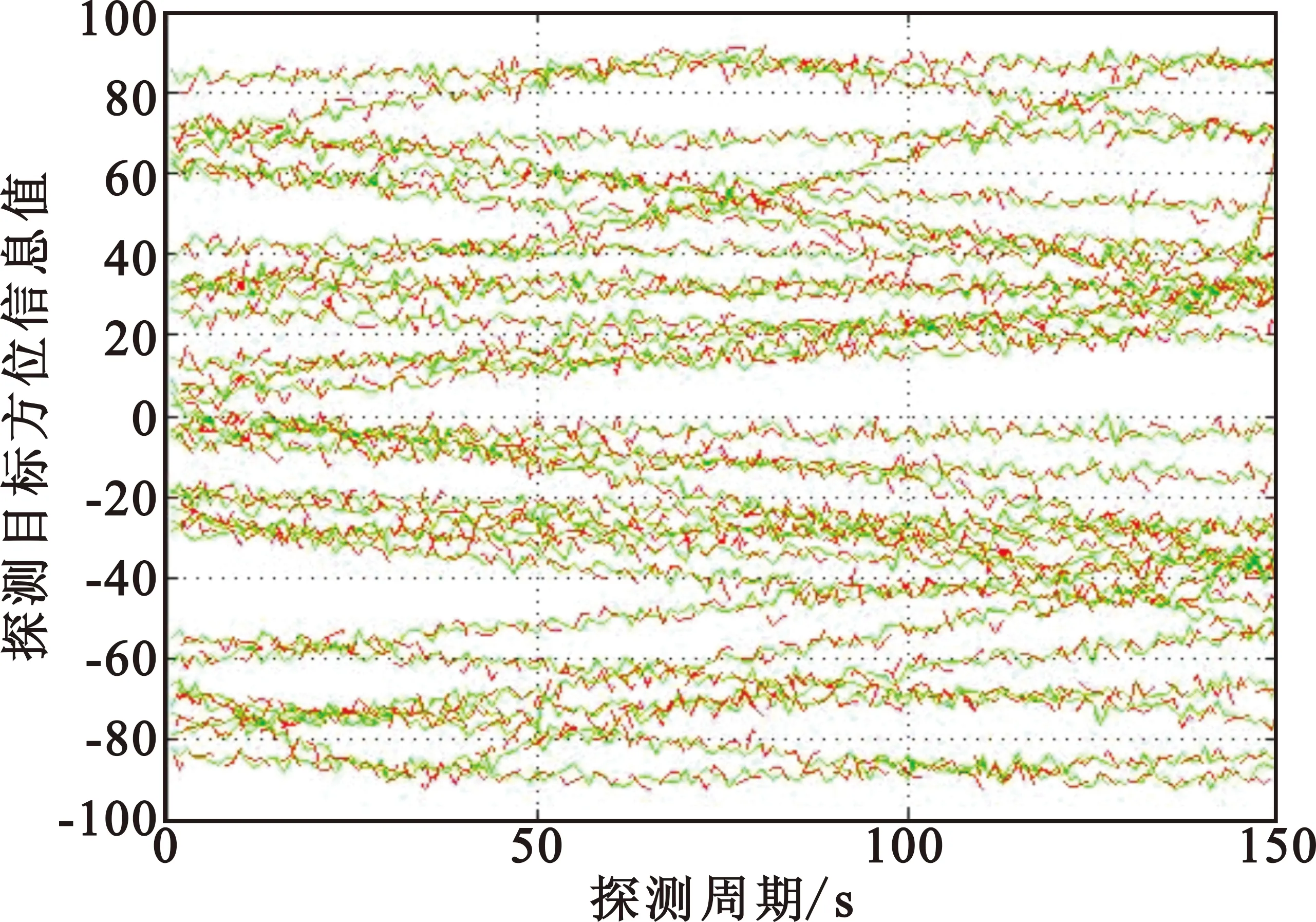
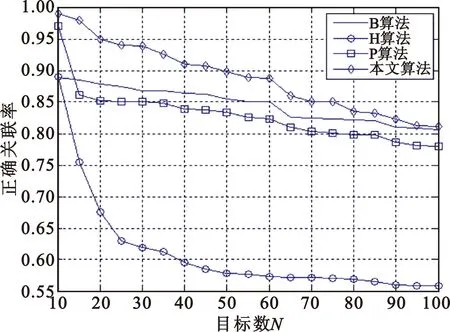
式中:ti 3.2 目标相似性衡量 假设在多目标较大量测误差情况下,假设其满足不同传感器的误差是零均值、方差恒定的高斯噪声,则构建其航迹关联的似然函数为 为了更有效地刻画目标运动相似性,构建目标的方位角变化率相似性似然函数: (7) 通过以上两者比较,可以较好地刻画目标运动,有效形成对目标航迹相似性的判断。 为了使其能够快速收敛,则取判证值为 Πi=Λi×Δi (8) 3.3 航迹关联算法描述 本文通过建立相似函数,完成对不同传感器间航迹相关性度量,在误差波动较大时,通过提高统计次数,可有效提高其统计量的关联程度。 实际应用中,传感器对目标的量测误差协方差很难获得,一般采用多拍求平均估计其协方差。 (1)同平台两无源传感器时间对准 将其方位信息根据公式(5)统一到相同时间点的方位信息集合。 (2)方位变换 测量角度信息变换到[0,2π]上,此时,将方位线进行霍夫变换。霍夫变换根据传感器位置及探测方位线值,不同时刻的传感器方位线通过霍夫变换后将形成目标方位线的点序列。为了描述简单,将传感器固定在坐标原点(0,0),则变换后为坐标轴上的一系列的点,因此将霍夫变换后的形式进行扩展,由于截距为0,则可以将目标点认为是(t,θ)域的一系列霍夫变换域的点。 (3)局部最优关联策略 全局关联以全部计算两两关联度为判决依据。根据实际经验,目标探测位置与传感器探测的误差水平有直接关系。针对变换域点关联策略,按照点航迹进行计算,则其关联矩阵构建以误差椭圆(以点为圆心、3δ误差为半径仅有角度维,因此椭圆变为圆)范围内可关联点作为关联对象: (θ-θt)2+(t-tt)2=(3δ)2。 (9) 考察该误差范围内所有关联点,对其一一建立关联矩阵。 目标关联的前提是目标距离间满足距离约束,因此建立目标方位角误差圆内关联矩阵进行关联分析,是一种符合实际的合理分析策略。根据传感器能力确定其误差范围,则可减少建立多义性处理矩阵的维度。 设角度误差满足如下条件: (10) (11) 根据此方法进行邻近方位线不同传感器相似性度量。由于此关联策略仅仅考虑误差范围内的传感器数据,因此获得关联是局部最优的,为了需求最优关联对,构建多义性关联矩阵。 (4)构建多义性度量矩阵 多义性度量矩阵一般以航迹关联矩阵进行描述: R=[rij]n1×n2。 (12) 式中: (13) 在同平台多传感器关联中,关联“鬼点”相对雷达组网要少得多。为了克服其出现的“鬼点”,本文采用统计量时间累积的方法进行克服,同时为了满足实时性要求,在传感器获取的各目标方位信息中,通过该变换后连续N点为周期进行特征序列构建并进行关联分析。即假设从第k个周期开始,则取k-N+1,k-N+2,…,k-1为变换域的方位点特征向量。 在航迹关联矩阵R中,如果对某一固定的i∈U1,存在两个以上的j所对应的rij为1,则根据最优关联策略,求取 rij=1,j∈{Πi1,Πi2,…,Πin}。 (14) 为了寻求航迹j的航迹最优关联方位,则选取其中值最小者: (15) 当求取的j值唯一时,则直接确定该值为最优者;否则,如果存在两个或以上关联方位,求取其中 j=argminjΛij,j∈{1,2,…,n}。 (16) 通过以上设置,可以获得最优的航迹关联对。 为了验证本文算法,构建了两部同一平台上的无源传感器。与实际环境相比,本文的环境设置是真实环境的简化,通过增加传感器可以类比真实环境试验。为了便于描述,假设平台坐标位于原点(0,0)m,模拟目标初始位置在[-200 km,200 km]×[-200 km,200 km]的区域内均匀分布,目标速度在4~100 m/s间均匀产生,航向在[0,2π]之间均匀产生,传感器量测周期设为6 s、10 s,仿真测试150个周期,目标按照上述要求匀速运动。目标个数N=30时,目标运动示意图如图2所示。 图2 目标运动示意图(N=30) Fig.2 Target motion schematic(N=30) 结合无源侦察获取的信息仅有方位信息,可以将目标获取的方位信息进行霍夫变换扩展后变换到(t,θ)域形式。图1中的目标运动方位角探测曲线如图3所示。 图3 目标运动参数域方位线变化曲线 Fig.3 Line of bearing in target motion parameter domain 无源传感器探测到的目标信息假设方位角误差均满足零均值正态分布,传感器1的方位量测误差的标准差为2°,传感器2的方位量测误差的标准差设为3°。加入误差后,则其目标方位线变化如图4所示。 图4 量测目标方位角变化曲线 Fig.4 Target azimuth measurement 为了便于说明问题,针对目标个数不同进行关联分析。给定目标个数为5,10,30,…,60,80,100批目标进行测试,传感器1的方位量测误差的标准差σ1=2°,传感器2的方位量测误差为σ1=3°,关联步长选择为N0=15。蒙特卡洛实验进行200次后取各点平均值获得图5~7结果。从图5可以看出,与其他3种算法比较,本文算法在目标数增多时关联正确率下降最慢。在实验中,由于目标之间信息缺失,误差影响成为关联的重要因素,究其原因,主要是由于关联中仅考虑关联度最高的传感器信息造成的;同时,本文采用局部最优获取最优算法,属于硬判决器,造成关联正确率变化,从多次实验平均值看,本文算法较其他算法具有较好的关联正确率。随着目标数目增多,关联正确概率整体都在下降,本文算法在100批目标时基本保证关联正确率在65%以上。 图5 目标正确关联率随目标数量变量变化曲线 Fig.5 Correctly-associated rate vs. target number 从图6中可以看出,随着关联目标数目的增加,4种算法的耗时均有所增加,其中H算法耗时随着目标数的增长快速增加,而其他算法则增加相对缓慢,本文算法由于仅考虑误差椭圆内的关联对,且取最优关联,因此其增速最慢。 图6 目标关联耗时随目标增加曲线 Fig.6 Target association time vs. target number 根据图5与图6分析可以看出,本文算法关联正确率与目标个数以及关联耗时都有所增加,在几种算法中,本文算法在目标较多的环境中具有一定优势;特别是在关联率近似相等的情况下,本文算法耗时和正确关联率均优于其他算法。 图7描述了算法在目标数相同情况下,关联正确率与量测误差关联曲线。考虑其不同相关序列进行误差分析,设定目标个数为N=60,传感器误差的方位误差的标准差为0.5°起始,以0.5°步长增加至5°进行考察,几种算法都可以有效关联且关联正确率均在90%以上,在误差达到1°左右时,其下降将明显增加。从几种算法比较来看,本文算法下降速度最慢,特别是在5°误差时,本文算法较最差算法的关联正确率高11%左右,说明该算法具有比较好的稳定性。 图7 目标正确关联概率随量测误差变化曲线Fig.7 Correctly-associated rate of target vs. measurement error 通过以上分析可知,本文算法在相同场景下,相关正确率在目标数增加、误差增大及关联时间上都比其他几种算法有一定提高,表明本文算法在同平台多传感器使用中具有抗噪能力高、时效性好、稳定性高等特点。 由于无源传感器探测信息缺维的特点,即仅有方位角信息,在航迹关联中存在信息量少、受误差影响大、关联难度大、一一比对耗时长等问题。本文在分析几种文献算法的基础上,提出了一种基于变换域局部关联策略的纯方位航迹关联方法。通过与其他航迹关联算法比较可以看出,本文提出的算法在目标较多情况下,正确关联率较其他算法有所提高,关联过程比较快,实时性能更优,算法效率更高。 随着探测能力的增强,传感器无源探测数据信息会不断增加,虽然本文算法较好地解决了纯方位关联问题,但是距离实际应用还有差距。如何利用传感器其他信息及目标实际运动情况,解决多角度多目标关联问题,将是进一步探索的方向。 [1] 贺文娇. 基于特征值和灰度关联的双机关联定位[J]. 电讯技术,2016,56( 4 ) :424-429. HE Wenjiao. Dual - aircraft correlation and localization based on characteristic value and gray correlative degree[J]. Telecommunication Engineering,2016,56(4) :424 -429.(in Chinese) [2] AZIZ A M.Fuzzy track-to-track association and track fusion approach in distributed multisensory-multitarget multiple-attribute environment[J]. Signal Processing,2007,87(6):1472-1492. [3] ARASARATNAM I,HAYKIN S. Cubature Kalman filters[J].IEEE Signal Processing Letters,2008,15(1):861-864. [4] 黄友澎,周永丰,谭秀湖,等. 基于B型灰色关联度的纯方位航迹关联算法[J].武汉理工大学学报(交通科学与工程版),2009,33(5):988-991. HUANG Youpeng,ZHOU Yongfeng,TAN Xiuhu,et al.Based on pure azimuth track association algorithm B gray relation of [J].Wuhan University of Technology(Transportation Science & Engineering),2009,33(5):988- 991.(in Chinese) [5] 郑庆利,关叶青.基于灰色关联分析的纯方位航迹关联算法[J].中国科技信息,2010(11):98-101. ZHENG Qingli,GUAN Yeqing. Bearings-track based on gray relational analysis correlation algorithms[J].China Science and Technology Information,2010(11):98-101.(in Chinese) [6] 孙顺,董凯,刘瑜,等.一种新的纯方位航迹关联方法[C]//第七届信息融合大会论文集.青岛:中国航空学会,2015:1201-1205. SUN Shun,DONG Kai,LIU Yu,et al.A new plain bearing track association method[C]//Proceedings of the Seventh General Assembly Information Fusion.Qingdao:Chinese Society of Aeronautics and Astronautics,2015:1201-1205.(in Chinese) 崔雨勇(1983—),男,山西襄汾人,2012年获博士学位,现为工程师,主要从事计算机视觉与信息处理。 CUI Yuyong was born in Xiangfen,Shanxi Province,in 1983. He received the Ph.D. degree in 2012.He is now an engineer. His research concerns computer vision and information analysis. Email:44989183@qq.com Local Optimal Bearing Track Correlation Based on Transform Domain CUI Yuyong (Southwest China Institute of Electronic Technology,Chengdu 610036,China) For the problem of bearing track correlation of passive sensors on the same platform,a local optimal track association algorithm based on transform domain is proposed.Bearing lines using Hough transform are mapped to equivalent parameter domain points which describe the different orientations in the method. A discrete point sequence with same time is formed by using alignment to build a discrete function of time.The recognition function is constructed and target correlation matrix is computed to meet the associated threshold.Optimal correlation relation is given by using local optimization method.The algorithm is shown better stability and less time and it provides a better solution to multi-sensor bearings on the same platform. passive detection;track association;local optimal;Hough transform;bearing line 10.3969/j.issn.1001-893x.2016.07.007 崔雨勇.基于变换域的局部最优纯方位航迹关联[J].电讯技术,2016,56(7):755-759.[CUI Yuyong.Local optimal bearing track correlation based on transform domain[J].Telecommunication Engineering,2016,56(7):755-759.] 2016-01-22; 2016-05-04 Received date:2016-01-22;Revised date:2016-05-04 TN971 A 1001-893X(2016)07-0755-05 **通信作者:44989183@qq.com Corresponding author:44989183@qq.com
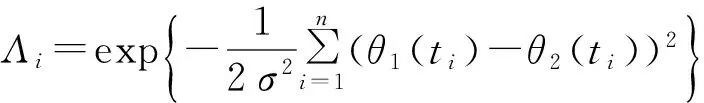
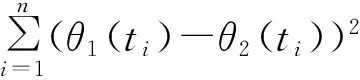
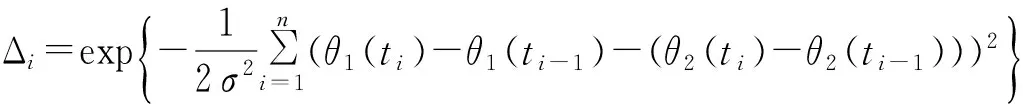
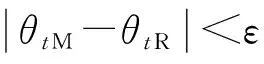
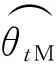
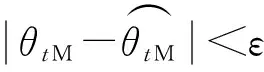
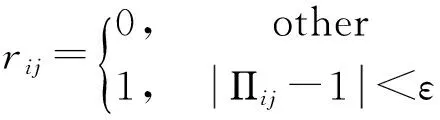
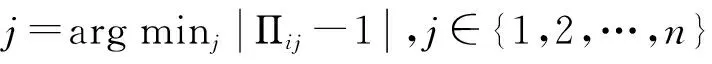
4 仿真分析
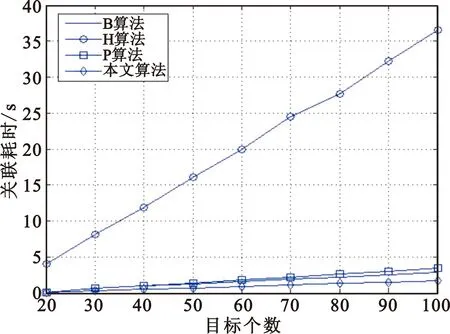
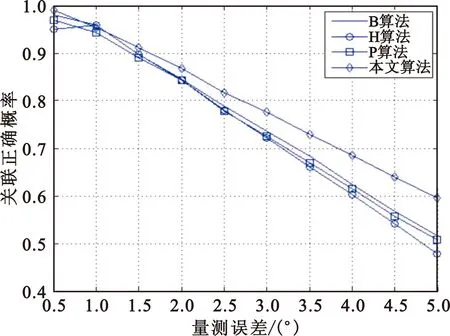
5 结束语

