基于振动模态观测器的TRUM两相协调控制优化运行

孙鹤旭，荆 锴，李国庆，董 砚

(1．河北工业大学，天津 300130；2．河北科技大学，石家庄 050018)



基于振动模态观测器的TRUM两相协调控制优化运行

孙鹤旭1,2，荆 锴1，李国庆1，董 砚1

(1．河北工业大学，天津 300130；2．河北科技大学，石家庄 050018)

根据行波型旋转超声电机两相振动模态与输出转矩的关系，提出了两相振动模态的协调控制的TRUM优化运行方法。首先，根据定子的等效电路模型，提出两相模态观测器的构建方法；其次，提出以一相模态为参考，动态地对另一相进行控制的协调控制方法，以达到两相模态幅值相等、相位互差90°的电机优化运行状态，从而减小输出转矩脉动，使电机运行更加稳定。最后，通过仿真和实验验证了所提出的控制方法的有效性。

行波型旋转超声波电机；振动模态；观测器；协调控制

0 引 言

行波型旋转超声波电机(Travelling-wave type Rotary Ultrasonic Motor，TRUM)是超声电机中应用较广泛的一种，其具有运行噪声低、转矩密度大、瞬态响应快、无电磁干扰、位置分辨率高等特点，通常用于高端精密运动控制系统[1]。

TRUM的运行机理是通过施加高频电压激发两相互差90°的振动模态，在定子中形成行波，从而通过定子表面质点的椭圆运动摩擦转子输出转矩。然而，TRUM的强耦合性、非线性等特点导致控制难度加大。国内外研究中，文献[2]实验分析了TRUM电压频率、相位的PI控制；史敬灼等采用线性化的特征模型，实现电压前馈的效率优化控制[3]，频率、电压双变量调速[4]等。上述控制均只是针对电机输入电压的相、幅、频进行的，直接从TRUM定子的振动实施控制的研究较为鲜见，文献[5]虽提出了针对振动的空间调相的相幅控制，但是是在电机结构改进的基础上进行的。

本文将针对定子振动直接进行控制，提出一种两相振动模态协调控制的运行方法，从TRUM定子等效电路模型基础上，以相电流、相电压构建电机的两相振动模态观测器，从而协调控制两相振动模态的幅值和相位，最终通过调节H桥驱动电路控制信号的占空比和相位实现对电机的稳定控制，减小输出转矩的脉动。

1 TRUM振动模态与转矩输出

根据压电陶瓷的逆压电效应，给TRUM两相压电振子上施加交变电压将分别激发出振动模态wA,wB，由于A、B两相的空间振型分布正交，两相模态在定子弹性体中激发出如下的一列行波：

(1)

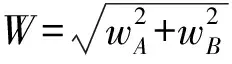
(2)

TRUM的输出转矩通常可以写成[6]：

(3)

式中：χ是与定转子接触边界位置、接触等速点位置相关的函数。当电机稳定运行时χ可近似认为是常数，则输出转矩Te正比于W，因此，只有在合成理想行波的条件下，电机输出转矩才可恒定。

在实际的控制过程中，由于两相振动模态不可直接测量，常通过直接控制两相电压幅值相等、相位差90°以获得理想的振动模态，但实际中由于电机两相参数无法做到完全一致，即使电压平衡的情况下振动模态也并不满足理想的要求，导致输出转矩会因行波波幅的变化而产生脉动，从而导致运行的不稳定。

2 TRUM两相协调优化运行方法

2.1 基于等效电路模型的振动模态观测器设计

TRUM的两相振动模态不可直接测量，但可以通过建立观测器对其进行观测。根据定子振动的机电耦合方程，TRUM定子振动可表示成如图1所示的两相等效电路的形式。

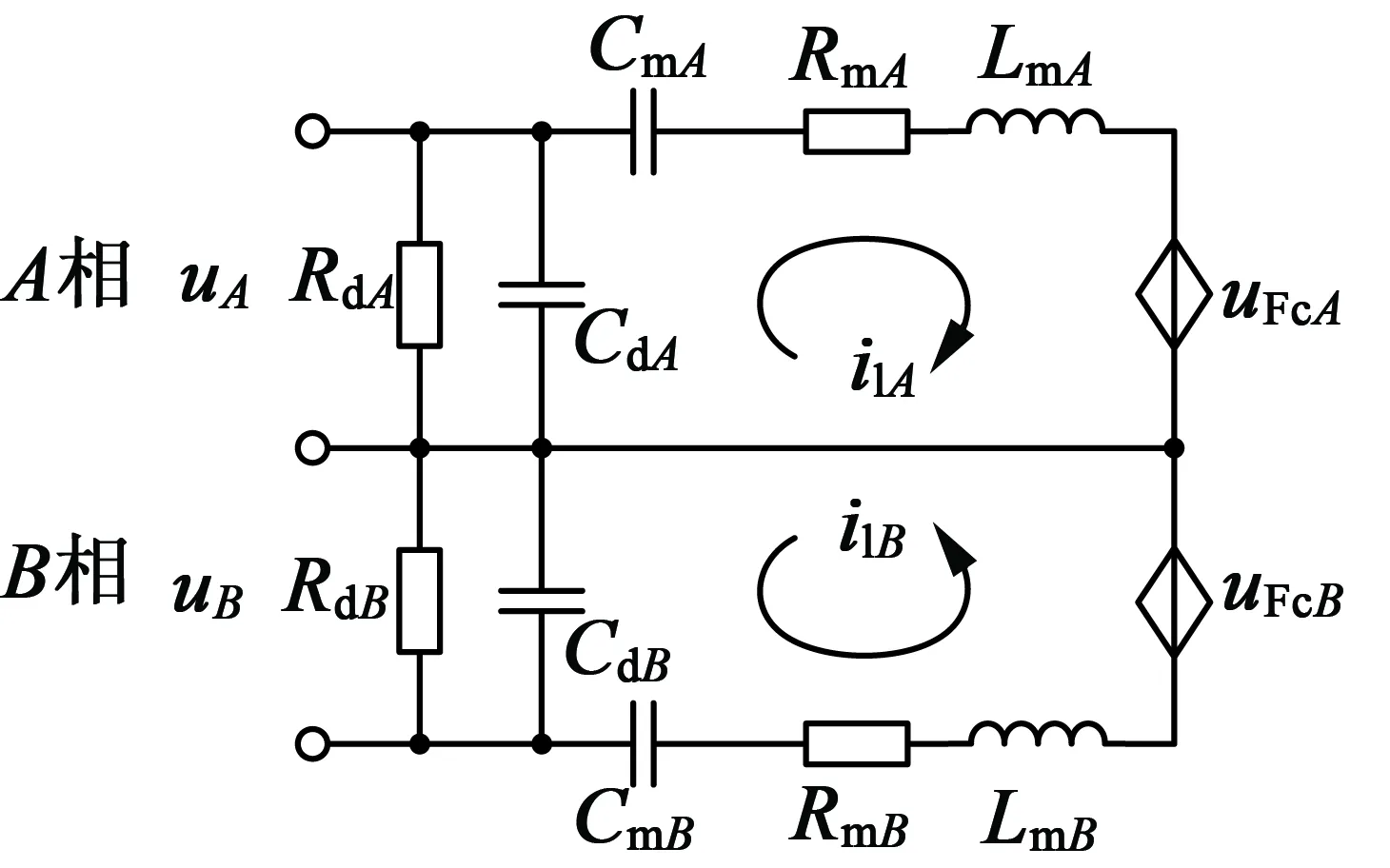
图1 等效电路模型

图1中，RdA，RdB为两相压电陶瓷的介电损耗电阻，CdA，CdB为两相压电陶瓷的静态电容，LRC支路参数CmA，CmB，RmA，RmB以及LmA，LmB，分别对应于两相的模态刚度、模态阻尼和模态质量。受控电压源uFrA，uFrB则表示两相界面接触模态力的反馈作用。并且LRC支路等效电流i1A，i1B与两相模态的一阶微分存在以下关系：

(4)

Θ为机电耦合常数。另外，根据输入电压电流可得：

(5)

则振动模态可由输入电流、电压来表示：

(6)

式中：RdA，RdB，CdA，CdB可通过测量得到，并且这些参数基本不受环境因素影响，故可通过检测电机的输入电压、电流，根据式(6)来计算电机两相的振动模态。

2.2 两相振动模态协调控制及运行方法

由于TRUM两相参数的差异，在施加等幅、同频的交流电时，两相模态幅值不相等。通常TRUM的H桥驱动控制器输出的最大电压是确定的，为控制两相模态幅值相等，相位互差90°，可选取在相同电压下振动模态较小的一相为参考，动态调节另一相的输入电压，以获得期望的振动模态。

如图 2所示为TRUM两相模态协调控制的控制框图。

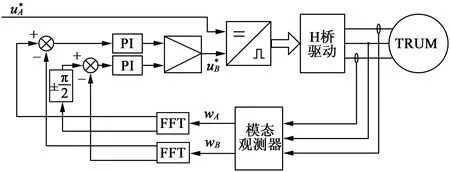
图2 两相振动模态协调控制框图

假设相同电压下A相的振动模态较小，取A相为参考。并设定A相H桥开关管控制信号占空比为50%，输出为最大电压。

通过高速A/D对电机两相电流电压采样，经模态观测器式(6)观测电机两相的模态值wA，wB，并通过FFT得到两相模态的幅值|wA|，|wB|和相角∠wA，∠wB，然后以A相为参考，通过PI控制获得如下的控制量：

(7)

式(7)中的“±”取决于电机的正反转。于是通过合理设置PI参数，可获得较为稳定的B相的给定电压，进而通过设置H桥驱动控制信号的占空比和相位实现对B向电压的控制。

此外，在该控制器基础上，增加转速或位置闭环，只需在一定条件下对A相给定电压进行控制即可实现。

3 协调控制方法的仿真与实验

本文仿真及实验采用TRUM-60型电机，电机的部分参数见表1所示。

在Simulink中搭建控制仿真模型，对本文方法进行控制仿真，并与常规H桥方波电压直接驱动的结果进行对比实验。控制驱动器采用H桥式LC谐振驱动器，H桥供电电压20 V，经1:5的升压变压器输出正负矩形波电压幅值为100 V，工作电压频率39.5 kHz。

表1 TRUM-60型电机参数

常规TRUM的H桥驱动中，A，B两均以正负电平各占50%的H桥输出方波电压直接驱动，其稳定运行时的相电压、电流、振动模态以及输出转矩的波形如图3所示。

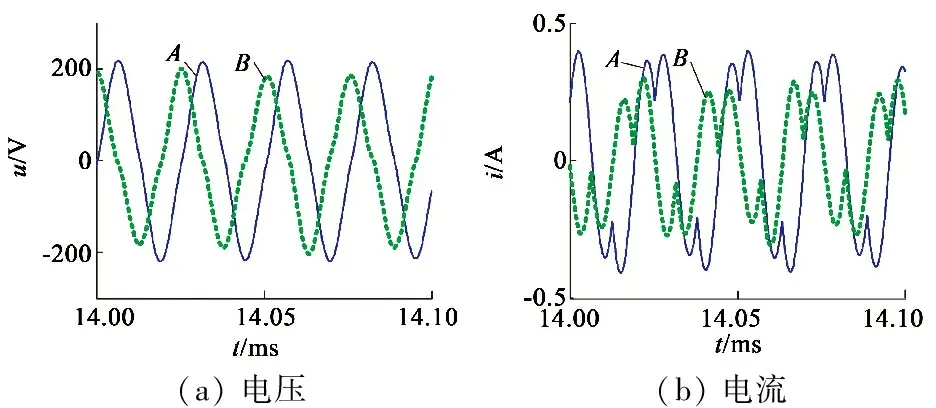
(a)电压(b)电流

(c)振态模态(d)转矩

图3 常规驱动控制结果

如图3(a)、图3(b)所示，两相输入电压是驱动器前端升压变压器输出100 V的方波电压经LC谐振升压后获得，幅值均达到200 V以上，并且A相的电压、电流均略大于B相。然而，由于定子结构参数的不一致，电机的工作频率更接近于B相的谐振频率，因此观测得到的B相振动模态大于A相，如图3(c)。在此情况下，驱动0.2 N·m的负载，输出转矩波形如图3(d)所示，其转矩在-0.18～0.39N·m之间变化，具有较大的转矩脉动。

相比较，采用本文的控制方法，A相保持与常规驱动相同的供电方式，而B相参考A相模态实施控制，电机稳定运行时，控制结果如图4所示。图4中，经模态协调控制，B相电压峰值降至130 V，与A相电压的相位差略小于90°，其电流幅值也响应减小，如图4(a)、图4(b)。而在此情况下，如图4(c)所示，两相振动模态达到幅值相等，相位差为90°的控制期望。同样驱动0.2 N·m的负载。此时的输出转矩仅有约±0.05 N·m的脉动(图 4(d))，相比前者，转矩脉动有了明显的减小。因此，采用本文的方法控制，对TRUM的稳定运行是有效的。

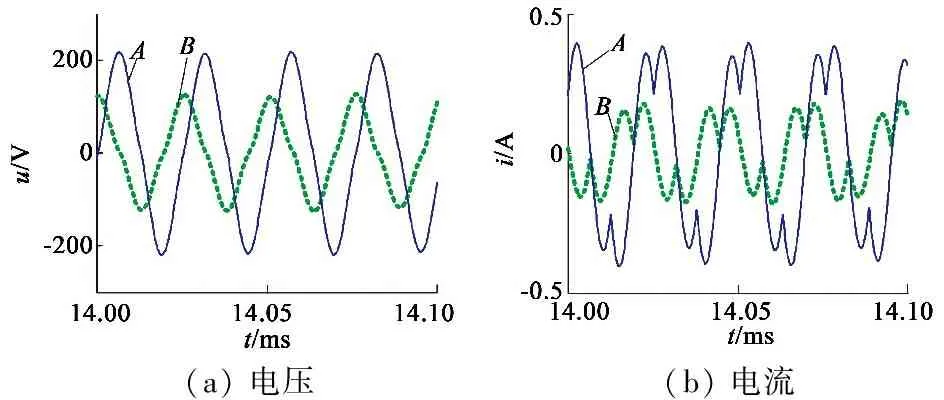
(a)电压(b)电流

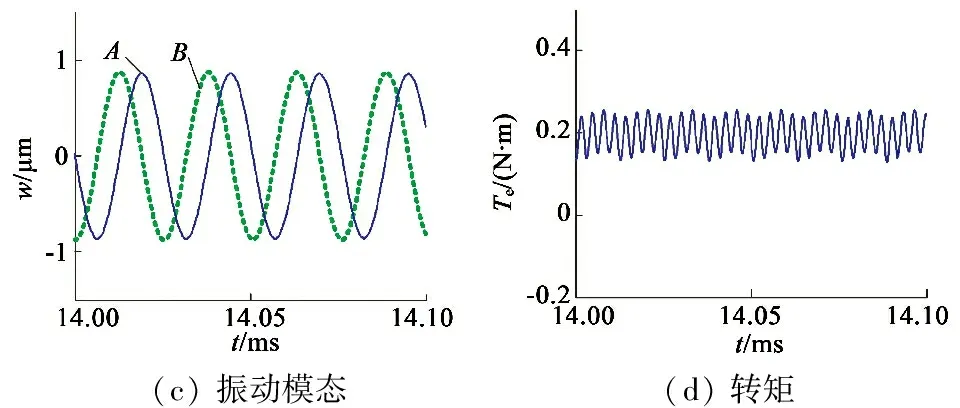
(c)振动模态(d)转矩

图4 本文方法控制结果

另外，通过测试平台实验对本文方法进行验证，测试平台如图5所示。

图5 TRUM实验测试平台

其中，TRUM控制器以DSP为控制核心，辅以CPLD逻辑单元输出控制H桥驱动电路的PWM信号，电流、电压采样由高速AD采样芯片构成。测试电机TRUM-60同轴连接至磁滞测功机，从而对上述两种方法的控制效果进行测试。

实验条件参数与仿真相同，负载转矩0.2N·m，可得到通常控制和本文方法在驱动恒定幅值情况下的输出转矩曲线，如图6所示。

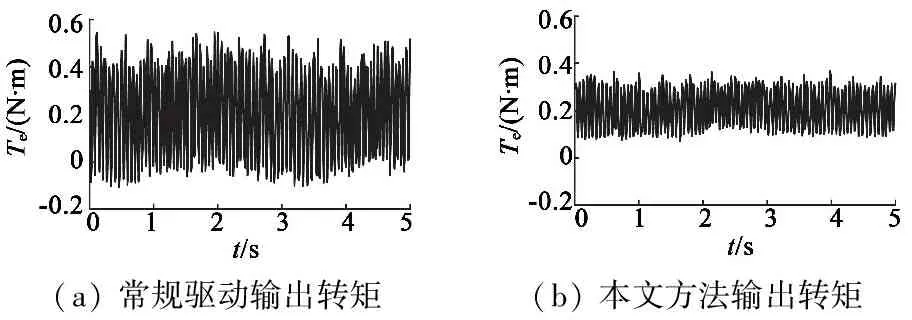
(a)常规驱动输出转矩(b)本文方法输出转矩

图6 两种控制方法的输出转矩曲线

从图6中可明显看出,在本文方法控制下，转矩脉动要小于通常的控制方法，电机运行更为平稳。

4 结 语

论文从TRUM定子振动出发，通过分析两相振动模态合成行波与输出转矩的重要关系，提出了直接控制两相振动模态的协调控制方法。方法通过建立振动模态观测器对两相振动模态动态观测，以其中一相为参考，动态调节另一相的控制电压的幅值和相位，以实现两相振动模态幅值相等、相位互差90°的控制期望。方法直接针对TRUM的定子振动进行控制，更有效地减小电机运行时的转矩脉动，提高电机运行的稳定性。论文最后通过仿真和实验，验证了本文所提两相振动模态协调控制方法在电机稳定运行控制中的有效性。

[1] 赵淳生.超声电机技术与应用[M].北京:科学出版社,2007.

[2] 李华峰,辜承林.使用PI控制的超声波电机精密位置控制[J]. 微电机,2002,35(2):23-26.

[3] SHI Jingzhuo,LIU Bo.Optimum efficiency control of traveling-wave ultrasonic motor system[J].IEEE Transactions on Industrial Electronics,2011,58(10):4822-4829.

[4] 史敬灼,王海彦.超声波电动机转速的双变量复合控制[J].微特电机,2010,38(5):42-44.

[5] 陆旦宏,胡敏强,金龙,等.基于空间调相的环形行波超声波电机的幅相控制[J].电工技术学报,2014,29(3):132-141.

[6] GIRAUD F，LEMAIRE-SEMAIL B，ARAGONES J，et al．Stability analysis of an ultrasonic motor for a new wave amplitude control[J]．IEEE Transactions on Industry Applications,2009，45(4)：1343-1350.

An Optimized Operation Method of Two-Phase Coordinated Control for TRUM Based on the Observer of Vibration Mode

SUN He-xu1,2, JING Kai1, LI Guo-qing1, DONG Yan1

(1.Hebei University of Technology,Tianjin 300130,China;2.Hebei University of Science and Technology,Shijiazhuang 050018,China)

An optimized operation method for travelling-wave type rotary ultrasonic motors was put forward by the coordinated control of two-phase vibration modes, in which the relationship of the vibration modes and the output torque was considered. Firstly, the observer of the two-phase vibration modes was built through the equivalent circuit model of the stator. Then, the coordinated regulation of dynamically controlling one phase mode by reference to the other phase was proposed to optimize the motor operation state, which expected the same mode amplitude and 90° phase difference of the two phases. By this method, the torque ripple will be reduced and the motor will run more steadily. Finally, the effectiveness of the method is verified by the simulations and experiments.

travelling-wave type rotary ultrasonic motor; vibration mode; observer; coordinated control

2015-09-07

河北省自然科学基金(E2013202108)；河北省重大科技成果转化项目(13041709Z)；河北省发改委项目(2013)

TM359.9

A

1004-7018(2016)10-0078-04

孙鹤旭(1956-)，男，教授，博士生导师，研究方向为运动控制、工程系统与控制。