由一道中考题说起
2016-12-19王欢
王欢
由一道中考题说起
王欢
例题如图1,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E,设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P.问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.
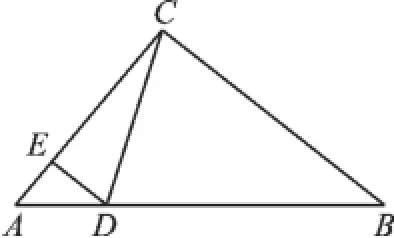
图1
这道是2015年杭州中考题的第22题第2小问,主要考查了等腰三角形的判定、三角形的有关概念,都是我们“平面图形的认识”里的内容.
近年来,中考命题突出了能力考查,简答题在形式和内容上都发生了很大变化.题目“源于教材,高于教材,活于教材”,“题在书外,理在书中,预料之外,情理之中”.题目设置更加灵活,角度多变,不再是教材知识的简单搬家.所以,我们在解答此类题型时也应掌握一定的解题方法和技巧:
1.认真审题,抓住关键字词和条件.
2.分析条件和问题,理清题目中的知识点.
3.抓住知识点,解决问题.
下面,老师就借助这道中考题,引导同学探讨如何来解决中考中的解答题.
【分析】主要条件有:①∠ACB=90°;②DE⊥AC;③以F,C,G为顶点的三角形与△EDC有一个锐角相等.
注意的字词:①BC>AC;②点D在AB边上,点F在线段EC上,点G在射线CB上.
问题是:判断CP是△CFG的什么线?
尤为引起疑问的一个条件是:“以F, C,G为顶点的三角形与△EDC有一个锐角相等”.△FCG和△EDC的哪个锐角相等?
一个引起疑问字词是:“D在AB上”,CD是什么线?是一般的线段还是特殊的线段?
通过尝试和思考可以画出三种示意图,发现此题可以分成三种情况讨论,其中图2,图3中CD是一般线段,图4中CD恰好是∠ACB的角平分线.这样,答案就非常明显了.

图2
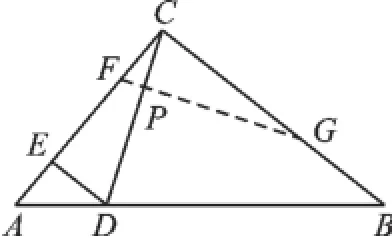
图3
【解答】①如图2,若∠CFG=∠ECD,此时线段CP是△CFG的FG边上的中线.
证明:∵∠CFG+∠CGF=90°,∠ECD+∠PCG=90°,又∵∠CFG=∠ECD,
∴∠CGF=∠PCG,∴CP=PG,
∵∠CFG=∠ECD,
∴CP=FP,∴PF=PG=CP,
∴线段CP是△CFG的FG边上的中线.
②如图3,若∠CFG=∠EDC,此时线段CP为△CFG的FG边上的高线.
证明:∵DE⊥AC,∴∠EDC+∠ECD=90°,
∵∠CFG=∠EDC,∴∠CFG+∠ECD=90°,
∴∠CPF=90°,
∴线段CP为△CFG的FG边上的高线.
③如图4,当CD为∠ACB的平分线时,CP既是△CFG的FG边上的高线又是中线.
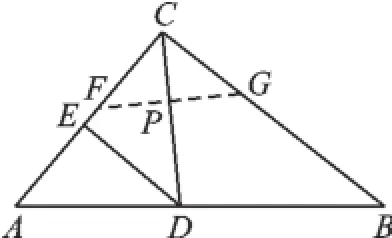
图4
