抓住基本图形巧添辅助线

张琼

抓住基本图形巧添辅助线

张琼

七年级同学们刚刚接触平面几何，难免会碰到需要添加辅助线的题目，此时，同学们普遍感觉这类题目比较难.许多同学常常会向老师提出这样的问题：“老师，为什么要添加这条辅助线？”要解决这些问题，同学们就要掌握添加辅助线更一般的规律.

平面几何可以通过不同图形的不同组合而发生无穷变化，一个几何问题，经过分析后，都一定会发现这样一个事实：它是由一个或若干个最简单最基本的图形组成的，我们把这些最简单最基本的图形称为基本图形.

如图1，已知AB∥CD.

求证：∠ABE+∠BEC+∠DCE=360°.

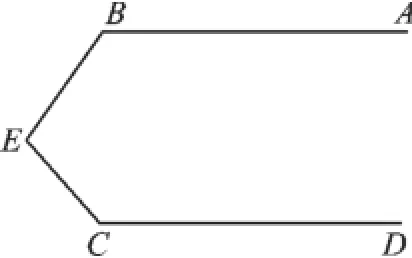
图1

首先，学会基本图形的识别.

人们常常感叹于优秀生反应快，并把原因归结为“此人天生聪颖”.实际上，优秀生之所以快，是因为他们善于将一些基本问题进行模块化，把它们的结构和图形储存在脑海中，到用的时候能迅速浮现出来.这好比电脑快是因为储存了大量的程序一样.因此，要想做到快速识别基本图形，平时就应当有意识地归纳和识记基本图形.譬如要解答此题，就应当先熟练掌握“两条平行线被第三条直线所截”的基本图形.

本题条件中出现了一组平行线：AB∥CD，所以考虑用“两条平行线被第三条直线所截”的基本图形进行证明.给出的图形中，发现基本图形不完整，所以需要添加辅助线，根据思考规律，分为两种情况：

①添加第三条直线；

②添加平行线.

其次，添加辅助线，构造基本图形.

实验组患者中有1例患者唾液增多,有1例患者失眠,不良反应发生率为12.5%;对照组患者中有1例患者唾液增多,有2例患者心动过速,有1例患者嗜睡,不良反应发生率为25.0%。实验组明显低于对照组,两组差异对比具有统计学意义,P<0.05。

（一）添加第三条直线

在给出的图形中，没有直接与AB、CD都相交的第三条直线，所以根据这个基本图形的思考规律，需要添加第三条直线.由于两平行线AB、CD可能被各种位置不同的第三条直线所截，所以就会出现添加辅助线的多种可能情况.

（1）若两平行线AB、CD被直线BC所截，由于图中没有直线BC，故连接BC，如图2.

证明（略）.

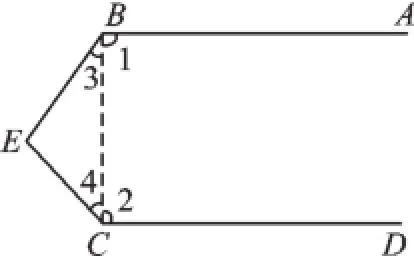
图2

（2）若两平行线AB、CD被直线BE（或CE）所截，由于BE与CD没有相交，所以基本图形不完整，故延长BE、DC交于F，如图3.

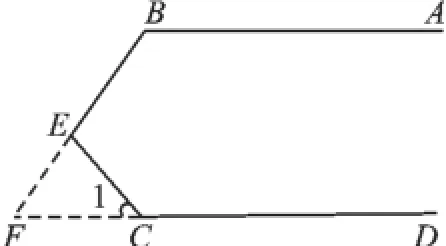
图3

证明（略）.

（3）若两平行线AB、CD被过点C且与AB、CD相交的直线所截，则可以过点C作CF交AB于F，如图4.

图4

证明（略）.

（二）添加平行线

若把BE（或CE）看作是截一组平行线的第三条直线，那么还缺少一条平行线，故过点E作EF∥AB.这里有两种情况：

（4）平行线AB、CD与EF构成同旁内角，如图5.

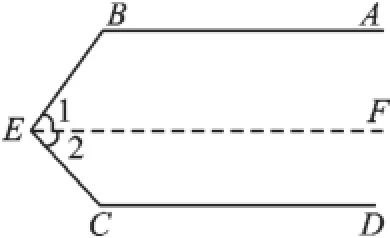
图5

证明（略）.

（5）平行线AB、CD与EF构成内错角，如图6.

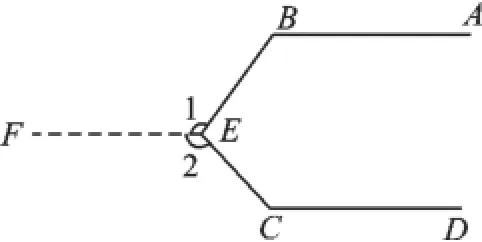
图6

证明（略）.

第三，对添加辅助线再思考.

基本图形的辅助线添加，首先需要根据题目条件和结论识别出基本图形，要做到这一点，需要在做完题后，进行如下的反思：自己是怎样想出来的？有没有别的方法？不同的解法有没有共同的东西？能把这个共同的东西应用于另外一些题目吗？如果发现这个思考方法具有普遍性，那么要把它整理出来，因为这就是一个基本图形.当我们总结的基本图形越多，再碰到相关题目的时候，就越容易识别基本图形，使之容易得到解决.

（作者单位：江苏省丹阳市华南实验学校）