基于各向异性Radon变换的叠前地震数据重建

王升超,韩立国,巩向博

(吉林大学地球探测科学与技术学院,吉林长春130012)



基于各向异性Radon变换的叠前地震数据重建

王升超,韩立国,巩向博

(吉林大学地球探测科学与技术学院,吉林长春130012)

基于常规双曲Radon变换进行叠前地震数据重建时,即使分辨率很高也难以得到准确的中远偏移距数据,因为地震信号同相轴在偏移距较远时已经不再满足双曲线假设。提出基于各向异性Radon变换,即由偏移距、慢度、非椭圆率三参数控制的各向异性Radon变换进行叠前地震数据重建的方法,考虑了偏移距较远时地震数据的非双曲线同相轴,通过稀疏约束控制Radon变换提高了地震数据的重建精度。针对时变Radon变换耗时较长的问题,在算子求解过程中采用快速迭代软阈值算法(Fast iterative shrinkage-thresholding algorithm,FISTA)加快了收敛速度,提高了计算效率。模拟数据和实际数据的应用结果表明,各向异性Radon变换方法在提高数据重建准确度和计算效率方面效果良好。

各向异性Radon变换;远偏移距;数据重建

地震数据受到施工条件、采集孔径、仪器故障等影响,难免会出现缺失及不规则的情况,对后续处理效果产生很大影响,特别是表面多次波衰减、波动方程偏移等基于多道处理的算法[1-4]。KABIR等[5]利用抛物Radon变换[6]重建近偏移距缺失数据,取得了良好效果,但只能处理规则采样数据,且需要多次迭代。SACCHI等[7]提出高分辨率Radon变换方法,并将其成功应用于近偏移距地震道重建,但在提高分辨率的同时增加了计算量。王维红等[8]提出并应用加权抛物线Radon变换法进行数据规则化和重建,在近偏移距地震数据重建中取得了良好效果。目前应用Radon变换进行数据重建的研究主要集中在提高分辨率和减小计算量两个方面,且多针对各向同性条件下的近偏移距地震数据。海上地震数据多为远偏移距,且深层陡倾角成像需要准确的远偏移距数据,准确重建偏移距较远的地震数据同样十分重要[9-10]。

相比于抛物Radon变换,双曲Radon变换分辨率更高,进行数据重建具有更高的精度。但目前使用双曲Radon变换重建远偏移距地震数据面临以下问题:①常规双曲Radon变换公式基于水平或中等倾角地质构造的反射同相轴在CMP道集上呈双曲线走时的假设,而偏移距较远的反射波同相轴已经不能用简单的双曲线走时公式进行准确描述;②双曲Radon变换具有时变属性,变换算子只能在时间域表示,利用共轭梯度法求解计算量巨大,这也是时间域求解Radon变换的固有问题[11-13]。本文提出各向异性Radon变换数据重建方法,将常规双曲变换公式改为由偏移距、慢度、非椭圆率三参数控制的各向异性变换公式[14];用FISTA算法[15]取代常规共轭梯度求解方法;采用稀疏约束控制各向异性Radon变换,通过正则化参数λ平衡反演误差与模型稀疏化程度[16]。理论模型和实际资料重建结果表明,本文方法对中远偏移距地震数据有着很好的重建效果。

1 方法原理

1.1 各向异性Radon变换原理

任意水平层状介质模型反射波走时方程可由级数展开得到与层厚、层速度及偏移距2阶、4阶、6阶等有关的复杂函数。当模型为各向同性且偏移距较小时(最大偏移距小于反射界面深度),可忽略4阶及更高阶项,用简单的双曲线公式来描述纵波反射同相轴。常规双曲Radon变换定义为:

(1)

式中:τ是截距时间;p是慢度(速度倒数);x是炮检距;d(t,x)为道集数据。

但长偏移距纵波反射同相轴时距曲线不满足双曲线规律,需用非双曲公式进行精确描述[17]。TSVANKIN[18]给出了水平单层各向异性介质长偏移距动校时差公式,ALKHALIFAH等[19]给出了该公式用动校速度和非椭圆率参数表示的形式。权衡计算精度与效率,本文采用ALKHALIFAH等[19]给出的非双曲时差公式定义了各向异性Radon变换,其正变换公式如下。

(2)

与常规Radon变换相比,各向异性Radon变换在包含高阶项的同时,增加了非椭圆率参数η,该参数与每个采样时刻一一对应。要想获得高精度的各向异性Radon变换域数据,需要准确的η值,因此如何求取实际数据的η值显得尤为重要。理论模型中的η值是已知的,对于实际地震数据,本文采用双参数速度分析的方法来求取准确的η值[20-21]。虽然各向异性Radon变换公式更加复杂,但是离散求解时矩阵的维数、大小未变,计算量与常规双曲Radon变换相当。

为避免数据重建时产生假频[22],得到高分辨率的采样结果,需要合理选择参数,下面讨论参数的选取准则。参数的采样率为:

(3)

已知p=1/v,则(3)式可化为:

(4)

令Δv=vk-1-vk,得:

(5)

当vk和vk-1比较接近时,vk≈vk-1,公式(5)变为:

(6)

设原始数据中最大有效反射速度为vmax,要使(6)式对所有的有效波场均成立,则式中vk应替换为vmax。同时,在CSP或CMP道集上做变换时,Δv选取的范围通常为50～100m/s,因而得到临界值关系如下:

(7)

确定了Δp的值后,根据p=1/v给出p的初始值p0和最大值pmax,就可以在不增加数据重建计算量的同时保证重建的准确性[15]。

1.2 稀疏约束反演

为了得到更准确的重建结果,本文在常规最小二乘反演的基础上,提出了基于稀疏约束的反演方法,采用正则化参数λ来平衡模型的稀疏化与反演误差,从而控制重建精度。高分辨率Radon变换通常先定义反变换,再通过求解最小二乘约束下的目标函数求取正变换。Radon变换反变换公式如下。

d=Lm

(8)

式中:d和m分别表示离散原始数据与Radon域数据的矩阵形式;L和LT分别为Radon变换算子和伴随变换算子。因Radon变换的非正交性,建立最小平方意义下的线性化反演误差目标函数,其范数条件的解为:

(9)

在时间域内进行稀疏约束可以很好地提高Radon域数据的分辨率。将Radon域数据作为稀疏条件进行约束反演,对反演误差取l2范数,对稀疏约束模型取l1范数,即通过线性反演问题的l1-l2混合范数求解,建立如下的目标函数:

(10)

式中:λ是正则化参数,用于平衡反演误差与模型的稀疏化,其值越大,Radon域内数据越稀疏。对于规则的模拟数据,λ通常取0,而对实际数据,合适的λ值可以使重建结果更加准确。

1.3 各项异性Radon变换求解算法

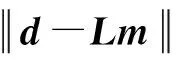
(11a)

rk+1=rk-αkA·pk

(11b)

(11c)

(11d)

pk+1=rk+1+βkpk

(11e)

(11f)

可见共轭梯度算法的递推步骤较多,在实际运算中收敛速度较慢。

为了提高计算效率,我们采用快速迭代软阈值算法(FISTA)加快反演的收敛速度,迭代更新公式如下:

m0=(LTL)z-1LTd

(12a)

x0=m0

(12b)

t0=1

(12c)

当k≥0时:

(13a)

(13b)

(13c)

式中:k是当前迭代次数;soft是取软阈值算子;a是Lipschitz常数,a≥max[eig(LTL)]。这样经过数次迭代就可以获得混合域高分辨率的Radon变换结果。

2 模型试算及实际资料处理

2.1 理论模型

为检验本文各向异性Radon变换数据重建方法的效果,建立了一个远偏移距数据模型,模拟地震记录共81道,道间距100m,每道500个采样点,采样间隔4ms,各向异性参数η取固定值0.1,如图1a所示。图1b为该模型不规则采样及缺失远偏移距数据的情况,即对原始数据前50道间隔抽样,且使第66至75道(共10道)远偏移距数据缺失。采用高分辨率双曲Radon变换和各向异性Radon变换分别进行数据重建,用FISTA算法迭代100次,其Radon域结果分别如图1c和图1d所示,重建后的结果分别如图1e和图1f所示。可以看出,各向异性变换使Radon域内聚焦效果更好,重建结果更接近原始数据,特别是远偏移距缺失数据的重建结果。

为进一步比较两种方法的重建误差,图2a和图2b分别给出了高分辨率双曲Radon变换和各向异性Radon变换重建数据与原始数据之差。图2c,图2d,图2e,图2f分别给出了原始数据、不规则缺失数据、高分辨率双曲Radon变换重建数据和各向异性Radon变换重建数据的f-k谱,对比可见,不规则缺失数据出现严重假频,两种Radon变换重建方法都能明显消除这些假频。为准确描述重建精度,定义重建误差如下:

(14)

高分辨率双曲Radon变换重建误差EΔ=9.84%,各向异性Radon变换重建误差EΔ=3.71%,各向异性Radon变换重建误差明显更小。

在求解各项异性Radon变换时,我们分别采用共轭梯度算法和FISTA算法进行了对比测试,运行环境为Intel(R)Core(TM)i5-2300 CPU@2.80GHz,8GB DDR3 1333MHz内存。FISTA算法在迭代100次的情况下重建误差为3.71%,耗时159.8s;共轭梯度法至少迭代150次才能使误差减小到4%以下,耗时为377.5s。可见FISTA算法不但计算效率高,而且收敛速度快。

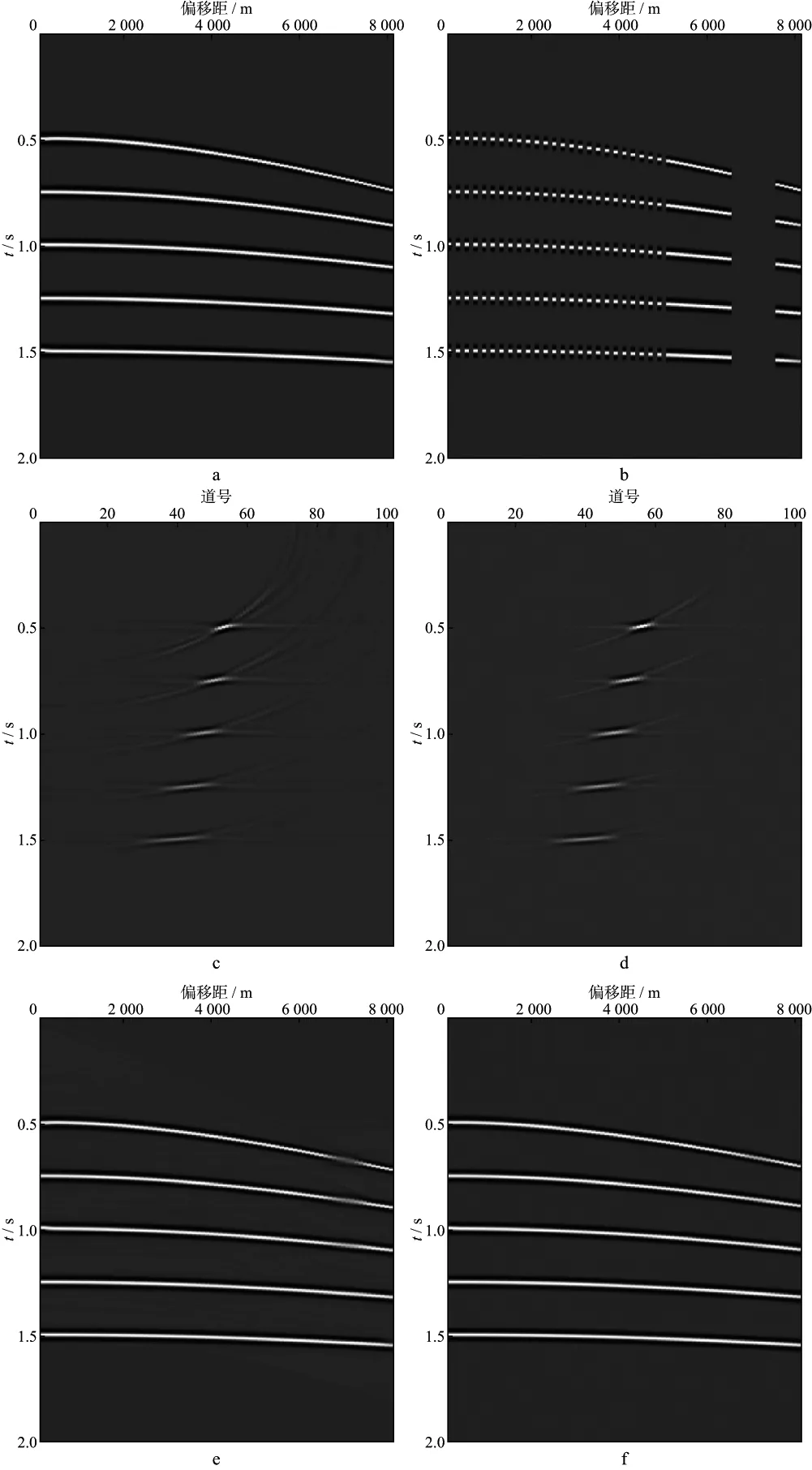
图1 模型数据重建a 原始数据; b 不规则缺失地震道数据; c 高分辨率双曲Radon变换结果; d 各向异性Radon变换结果; e 高分辨率双曲Radon变换重建结果; f 各向异性Radon变换重建结果

图2 重建误差对比a 高分辨率双曲Radon变换重建误差; b 各向异性Radon变换重建误差; c 原始数据f-k谱; d 不规则缺失数据f-k谱; e 高分辨率双曲Radon变换重建数据f-k谱; f 各向异性Radon变换重建数据f-k谱

2.2 实际数据处理分析

采用我国某地区实际地震资料CMP道集,验证本文各向异性Radon变换数据重建方法的实用性。该数据共126道,道间距24m,每道626个采样点,采样间隔4ms,记录长度2.5s,其中有效反射波的速度范围在1200～1600m/s。进行各向异性Radon变换数据重建之前,首先对道集进行双参数速度扫描,得到每个地震同相轴所对应的η参数,即扫描得到的η参数与同相轴个数相同;然后将η参数按时间方向插值,得到每个离散时间采样点对应的η值,如图3所示。

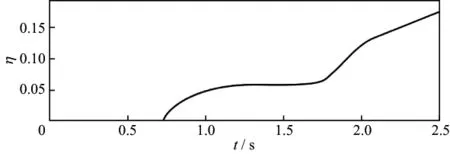
图3 双谱分析所得η参数曲线

图4a是原始实际数据,图4b是对实际数据前50道间隔抽样并缺失第101到110道远偏移距数据的结果,图4c为其各向异性Radon变换的结果,图4d 为各向异性Radon变换方法数据重建结果。可以看出实际数据重建效果较好,说明本文方法具有较强的实用性。分别对原始实际数据及其不规则缺失地震道数据和重建后数据做f-k谱分析,结果如图5a,图5b,图5c所示,可见不规则缺失地震道数据出现了明显假频,利用本文方法重建数据后有效地消除了这些假频。

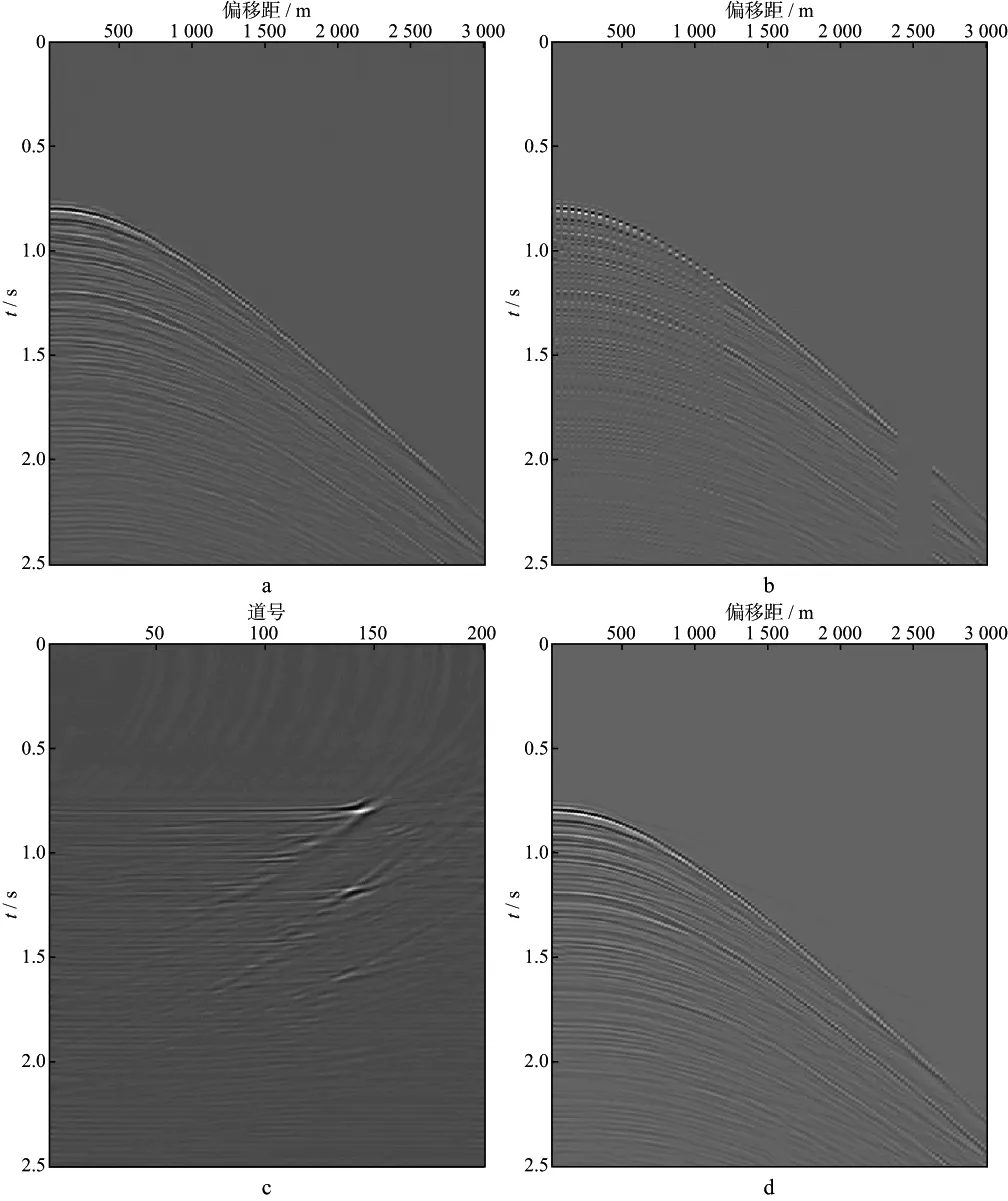
图4 实际数据处理a 原始实际数据; b 不规则缺失地震道数据; c 实际数据各向异性Radon变换结果; d 实际数据各向异性Radon变换重建结果

为进一步提高各向异性Radon变换重建效果,在实际数据处理中加入一定程度的稀疏约束,并取实际数据与重建数据的第101至110道进行对比。λ的取值范围一般为0.0001～0.0100,在该区间用二分法求解λ,仅需求解几次即可得到最佳λ值0.002。图6a为实际数据第101至110道,图6b为常规Radon变换的重建结果,图6c为λ=0时的各向异性Radon变换重建结果,图6d为λ=0.002时的各向异性Radon变换重建结果。图6b,图6c,图6d重建误差分别为11.84%,6.52%,5.04%,说明各向异性Radon变换重建效果更好,且λ=0.002时重建结果更接近实际数据。

图5 原始数据(a),不规则缺失数据(b)及重建数据(c)f-k谱

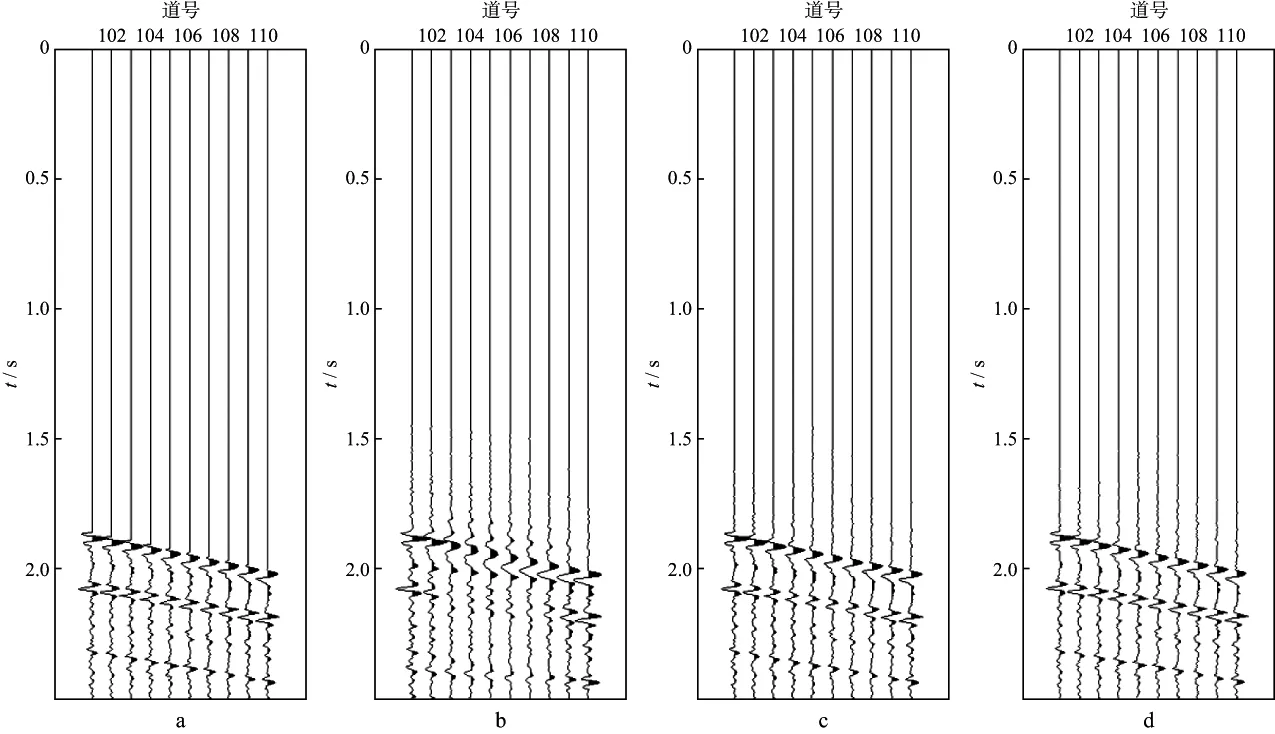
图6 实际数据重建位置对比a 缺失位置的实际数据; b常规Radon变换重建结果; c λ=0时各向异性Radon变换重建结果; d λ=0.002时各向异性Radon变换重建结果

3 结束语

本文提出的各向异性Radon变换重建方法可以更好地恢复远偏移距地震数据,弥补了常规Radon变换方法在远偏移距数据重建方面的不足。对于不同地区的实际数据,各向异性Radon变换前需进行双参数速度扫描,获得相应正确的各向异性参数η,确保Radon域内数据的高分辨率。采用稀疏约束反演的方法可以减小数据重建误差,得到更为准确的重建结果。在时间域Radon变换的求解过程中,采用FISTA算法取代常规的共轭梯度算法可以加快收敛速度,提高运算效率。

[1] 李庆忠.走向精确勘探的道路[M].北京:石油工业出版社,1994:98-112 LI Q Z.The way to obtain a batter resolution in seismic prospection[M].Beijing:Petroleum Industry Press,1994:98-112

[2] 黄新武,吴律,牛滨华.基于抛物线拉东变换的地震道重构[J].中国矿业大学学报,2003,32(5):534-539 HUNG X W,WU L,NIU B H.Reconstruction of seismic trace by parabolic Radon transform[J].Journal of China University of Mining & Technology,2003,32(5):534-539

[3] 李远钦.一种非线性Radon变换及非零偏移距VSP波场分离[J].石油物探,1994,33(3):33-39 LI Y Q.A non-linear Radon transform and non-zero offset VSP wave field separation[J].Geophysical Prospecting for Petroleum,1994,33(3):33-39

[4] 曾有良,乐友喜,单启铜,等.基于高分辨率Radon变换的VSP波场分离方法[J].石油物探,2007,46(2):115-119 ZENG Y L,YUE Y X,SHAN Q T,et al.VSP wave filed separation based high resolution Radon transform[J].Geophysical Prospecting for Petroleum,2007,46(2):115-119

[5] KABIR M M N,VERSCHUUR D J.Restoration of missing offsets by parabolic Radon transform[J].Geophysical Prospecting,1995,43(3):347-368

[6] HAMPSON D.Inverse velocity stacking for multiple elimination[J].Journal of the Canadian Society of Exploration Geophysicists,1986,22(1):44-55

[7] SACCHI M D,ULRYCH T J.High-resolution velocity gathers and offset space reconstruction[J].Geophysics,1995,60(4):1169-1177

[8] 王维红,裴江云,张剑锋.加权抛物Radon变换叠前地震数据重建[J].地球物理学报,2007,50(3):851-859 WANG W H,PEI J Y,ZHANG J F.Prestack seismic data reconstruction using weighted parabolic Radon transform[J].Chinese Journal of Geophysics,2007,50(3):851-859

[9] 张红梅,刘洪.基于稀疏离散τ-p变换的非均匀地震道重建[J].石油物探,2006,45(2):141-145 ZHANG H M,LIU H.Sparseness discreteτ-ptransform in irregular seismic trace reconstruction[J].Geophysical Prospecting for Petroleum,2006,45(2):141-145

[10] 李晶晶,孙成禹,谢俊法.相对保幅的抛物线Radon变换法地震道重建[J].石油物探,2014,53(2):181-187 LI J J,SUN C Y,XIE J F.Seismic trace reconstruction by relative amplitude preserved parabolic Radon transform[J].Geophysical Prospecting for Petroleum,2014,53(2):181-187

[11] 孙成禹,尚新民,石翠翠,等.影响地震数据相位特征的因素分析[J].石油物探,2011,50(5):444-454 SUN C Y,SHANG X M,SHI C C,et al.Analysis of influence factors on phase characteristics of seismic data[J].Geophysical Prospecting for Petroleum,2011,50(5):444-454

[12] 刘法启,张关泉.借助广义 Radon变换进行方位角校正[J].石油物探,1996,35(4):43-51 LIU F Q,ZHANG G Q.Azimuth correction with the aid of generalized Radon transform[J].Geophysical Prospecting for Petroleum,1996,35(4):43-51

[13] 张军华,吕宁,雷凌,等.抛物线拉冬变换消除多次波的应用要素分析[J].石油地球物理勘探,2004,39(4):398-405 ZHANG J H,LV N,LEI L,et al.Analysis of application factors in multiple attenuation by parabolic Radon transform[J].Oil Geophysical Prospecting,2004,39(4):398-405

[14] 巩向博,韩立国,李洪建.各向异性Radon 变换及其在多次波压制中的应用[J].地球物理学报,2014,57(9):2928-2936 GONG X B,HAN L G,LI H J.Anisotropic Radon transform and its application to demultiple[J].Chinese Journal of Geophysics,2014,57(9):2928-2936

[15] TRAD D,ULRYCH T,SACCHI M.Latest views of the sparse Radon transform[J].Geophysics,2003,68(1):386-399

[16] BECK A,TEBOULLE M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202

[17] 尤建军,常旭,刘伊克.VTI介质长偏移距非双曲动校正公式优化[J].地球物理学报,2006,49(6):1770-1778YOU J J,CHANG X,LIU Y K.Optimization of nonhyperbolic moveout correction equation of long offset seismic data in VTI media[J].Chinese Journal of Geophysics,2006,49(6):1770-1778

[18] TSVANKIN T.Nonhyperbolic reflection moveout in anisotropic media[J].Geophysics,1994,59(8):1290-1304

[19] ALKHALIFAH T,TSVANKIN I.Velocity analysis for transversely isotropic media[J].Geophysics,1995,60(5):1550-1566

[20] ABBAD B,URSIN B,RAPPIN D.Automatic nonhyperbolic velocity analysis[J].Geophysics,2009,74(2):U1-U12

[21] 张博,韩立国,谭尘青.VTI介质平移初至走时动校正双参数反演[J].石油物探,2012,51(2):119-124 ZHANG B,HAN L G,TAN C Q.Shifted first-arrival travel time NMO velocity andηinversion for VTI media[J].Geophysical Prospecting for Petroleum,2012,51(2):119-124

[22] 王立歆,李强,姬小兵,等.用Radon变换法消除沙丘鸣震的应用及效果分析[J].石油物探,2002,41(1):89-91 WANG L X,LI Q,JI X B,et al.Application of Radon transform to elimination of dune ringing and its effect analysis[J].Geophysical Prospecting for Petroleum,2002,41(1):89-91

[23] 张保卫.Radon变换及其在地震数据处理中的应用[D].西安:长安大学,2007 ZHANG B W.Radon transform and its application in seismic data processing[D].Xi’an:Chang’an University,2007

[24] 熊登,赵伟,张剑锋.混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J].地球物理学报,2009,52(4):1068-1077 XIONG D,ZHAO W,ZHANG J F.Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple.[J].Chinese Journal of Geophysics,2009,52(4):1068-1077

(编辑:戴春秋)

Prestack seismic data reconstruction by anisotropic Radon transform

WANG Shengchao,HAN Liguo,GONG Xiangbo

(CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130012,China)

Although the conventional hyperbolic Radon transform owns high resolution to reconstruct seismic data,it is difficult to reconstruct the far-offset seismic data,because the event of far-offset seismic signals is no longer satisfied with the hyperbolic assumption.Therefore,we proposed a prestack seismic data reconstruction method by anisotropic Radon transform to consider the effect of far-offset factor.The formula of anisotropic Radon transform is controlled by offset,slowness and anellipticity.The travel-time curve of horizontal layer can be accurately described for far-offset by the anisotropic anellipticity parameter of the non-hyperbolic moveout formula.We also use sparsity constraint to improve the accuracy of reconstruction.During the procedure of operator solving,fast iterative shrinkage-thresholding algorithm (FISTA) is used to speed up the convergence and reduce the calculation time.The results of theoretical model and field data demonstrate that anisotropic Radon transform has good effect on the reconstruction accuracy and calculation efficiency.

anisotropic Radon transform,far-offset,seismic data reconstruction

2016-01-14;改回日期：2016-03-11。

王升超(1990—),男,硕士在读,从事地震勘探处理技术研究。

国家自然科学基金项目(41204078)资助。

This research is financially supported by National Natural Science Foundation of China (Grant No.41204078).

P631

A

1000-1441(2016)06-0808-08

10.3969/j.issn.1000-1441.2016.06.005