多李群核覆盖学习算法在图像分类上的应用
2016-12-19吴鲁辉李凡长
吴鲁辉,李凡长
苏州大学 计算机科学与技术学院,江苏 苏州 215000
多李群核覆盖学习算法在图像分类上的应用
吴鲁辉,李凡长+
苏州大学 计算机科学与技术学院,江苏 苏州 215000
WU Luhui,LI Fanzhang.Multiply Lie group kernel covering learning algorithm for image classification. Journal of Frontiers of Computer Science and Technology,2016,10(12):1737-1743.
李群具有代数结构也具有流形几何结构。将数据映射到多李群空间,并根据李群样本点在李群流形上的轨道关系,对那些同伦的轨道加以覆盖,从而使得覆盖域呈现出类别信息。利用核函数的思想,进一步使得类别不同的覆盖域更具有可分性,同时覆盖边界更具有光滑性,因此提出了多李群核覆盖学习算法。在MNIST手写体数字图像上进行了多组实验验证,并对实验结果进行了分析,结果表明与多连通李群覆盖学习算法相比,多李群核覆盖学习算法具有较好的分类效果。
李群;流形结构;覆盖学习算法;核函数
1 引言
现实世界的数据具有多样性和复杂性,数据的空间结构信息往往蕴含着更多有效信息,能够对数据分析提供有力支撑。建模数据的空间结构的一种有效方式是流形,但是没有有力的数学工具作为流形可计算方式,最终还是利用流形局部同胚与欧式空间这个特点,将数据映射到欧式空间进行研究,处理完成后再映射回流形上。这种方式代价高,而且很难寻找到一个合适的流形结构。
李群不仅是一个群,也是一个微分流形。李群既能够表示数据所在的流形结构,也提供了一套完整可计算理论。近年来,越来越多的计算机学者开始熟知李群,并将李群引入到与计算机相关的各领域中。文献[1]给出了李群机器学习的公理系统和基本模型。文献[2]利用流形上样本点的内均值求解方式,提出了李群均值学习算法。文献[3]给出了基于李群的半监督学习算法,从而使得可以利用未知类别的李群样本以改进李群学习器的性能。文献[4]从深层结构出发,提出了基于李群的深层结构学习算法,从而能够获得原始数据中更抽象更具有不变性的特征。文献[5]利用李群正态分布抽取状态样本,提出了一种基于李群正态分布的粒子滤波算法,提高了跟踪算法的效率和鲁棒性。文献[6]将系统状态空间中动力演化建模成李群,然后利用自由坐标李群积分来提高受限多体系统(multibody system,MBS)的准确率。文献[7]通过探索动作的李群结构来估计全局动作以及相对测量间估计误差的协方差,提出了一个基于矩阵李群的高斯分布表示的生成模型,从而构建了一个更好的姿势回归模型。
文献[8]从多连通李群空间中的道路同伦等价关系出发,得出同一类别的道路是同伦等价的,从而构成一个道路等价类,并用最优道路表示来近似表示类别的道路等价类,从而提出了多连通李群覆盖学习算法。多连通李群覆盖学习算法克服了经典覆盖学习算法不能很好对待特征缺失和异常特征突出的问题。在处理分类问题遇到提取的样本特征较少且不具有代表性时,具有明显的分类优势。文献[9]对多连通李群覆盖学习算法中的道路存在的选择和交叉问题做了进一步优化。文献[8]通过采样图形样本形状上的若干点构成的点云,来将原始样本映射为SO(2)空间中的李群样本。这种方式具有一定的局限性。
本文考虑利用样本特征的协方差矩阵来将样本映射为李群样本,通过特征之间的关系矩阵在李群流形上的空间关系对样本的类别进行研究。为了使同类样本在李群流形上的轨道更具有可分性,本文考虑将李群覆盖学习和核方法相结合,提出了多李群核覆盖学习算法,以增强模型的抗干扰能力以及使覆盖域更具有可分性。最后利用多李群核覆盖学习算法对研究对象进行分类。
本文组织结构如下:第2章简单介绍相关的基础知识,并利用图像协方差矩阵将图像样本映射为李群样本;第3章提出了多李群核覆盖学习算法;第4章通过若干个实验验证了本文提出的多李群核覆盖学习算法的性能;第5章给出结论和展望。
2 相关概念介绍
2.1 李群中的覆盖学习
李群[10-12]G是一种连续群,其每个元素都可以用一组在欧式空间一定区域内连续变化的独立实参数表示。参数的变化区域称为群空间。一般取李群恒元e的参数为0,故恒元的邻近元素称为无穷小元素。无穷小元素与任意李群元素M的乘积仍然是该李群的元素,且结果是M的邻近元素。将无穷多个无穷小元素与M相乘得到M′,那么在群空间就表现为从M在群空间对应的元素A到M′对应元素B的一条连续曲线,称该条曲线为从M到M′的道路。任意李群元素M在群空间中的对应点A与恒元e对应元素之间的连续曲线,称为该点M的道路。依据同伦等价关系可以将李群元素的道路分成若干组。每组构成一个道路等价类。组数称为群空间的连通度。当李群的群空间是多连通的时候,则该群真实表示是多值表示。
对应于学习问题,可以利用李群样本道路之间的某种关系来和本文的研究目的建立特定联系,以道路来建模研究目的。比如,对于分类问题而言,由于同类样本映射到李群空间的群元素的独立实参数是相似的,那么它们在群空间上的道路是同伦等价的,故它们在同一个道路等价类中。而直接求解某个道路等价类是困难的。通过分析多连通李群的性质可知,李群元素M的某个邻近区域内的道路是同伦等价的。这样,利用邻域覆盖思想,可以近似地去逼近道路等价类,从而实现对未知样本的分类。
文献[8]利用最优道路表示来覆盖道路等价类,提出了多连通李群覆盖学习算法。但是,多连通李群空间中的道路是复杂的,除去覆盖方式中覆盖半径容易造成的误判和拒识现象外,道路的选择和交叉问题也是造成误判和拒识的两个原因。本文考虑利用核函数来减弱道路之间的交叉问题。
2.2 图像的区域协方差特征
一幅图像可以表示为I,每个像素的属性可以表示为I(x,y)。那么,图像特征F可以表示为F(x,y)= Φ(I,x,y),其中函数Φ可以表示任何与图像属性相关的映射,例如灰度值、颜色和梯度值等。取图像I中所关心的局部区域R⊆F,区域R内的所有像素对应的Φ值可以表示为,其中zi为d维向量,n为区域R内的所有像素的个数。R区域内的向量集构成的协方差矩阵为:

图像协方差矩阵[13-14]内的任意两个点P1、P2之间的距离由文献[15]给出:


其中i=1,2,…,d且xi≠0。可以证明式(2)的d满足内积空间度量的几条公理,因此满足正定矩阵的李群结构。
3 多李群核覆盖学习算法设计与分析
将原始样本图像进行分块,得到N个分区域。对于每个区域提出一些特征,构成特征向量s∈Rd。然后,对特征向量集合FS={s1,s2,…,sN}求协方差矩阵,从而将原始样本映射为李群样本。如图1所示,将手写体字0的一幅图像分成4个分块,从每个小块中提取出d维特征。然后,对这些特征求协方差矩阵。从而将一幅图像表示成由特征关系构成的矩阵李群元素。
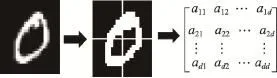
Fig.1 Block representation of an image图1 图像的分块表示
群与群之间存在着覆盖关系,从而构成覆盖群。覆盖关系是由覆盖映射定义的。由于直接寻找覆盖映射是困难的,通过元素之间的道路关系进行表示。模式识别理论指出,低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分。但是这种技术存在确定非线性映射函数的形式、参数和特征空间的维数等问题。核函数却有效避免了这些问题。核函数[16-19]的形式和参数会隐式地改变从输入空间到特征空间的映射,进而对特征空间的性质产生影响。本文希望利用核距离来度量李群样本之间的相似性,并在该距离的基础上对覆盖邻域进行求解,以使得模型具有更好的抗干扰能力和覆盖区域更具有可分性。
机器学习中,经常使用的高斯核函数是:

由于d(M1,M2)=d(M2,M1),能推出K(M1,M2)=K(M2, M1),故K(M1,M2)满足对称性。利用文献[20]中的方法可以证明K(M1,M2)是非负定的。因此,上述定义的李群高斯核函数满足Mercer定理,故李群高斯函数K(M1,M2)是一个核函数。
李群流形上,两李群样本间测地线距离定义为:

其中,M1、M2是两个李群样本;ln是以e为底的矩阵对数运算;||⋅||是Frobenius范数。根据Baker-Campbell-Hausdorff公式[21]并对其进行一阶近似,可以近似求得两个李群元素之间的测地线距离,即:
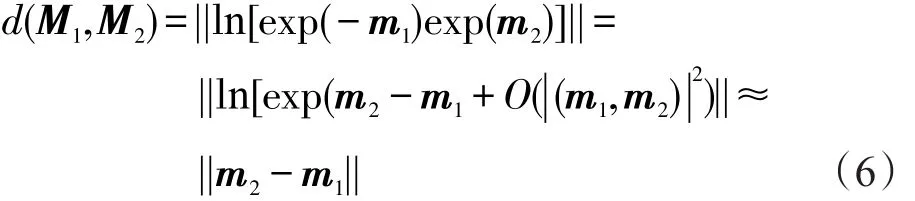
其中,m1、m2分别是M1、M2在单位元I处的李代数。
李群高斯核函数用于衡量两李群样本之间的相似性(距离)。相似性较高的样本,李群高斯函数的输出较大,而相异性较高的样本,李群高斯函数的输出值较小。经过这种核距离变换,可以使求得的覆盖域更具有可分性,能够减弱道路交叉情况。同一类别样本属于同一覆盖群,那么某李群样本M1的覆盖邻域为:

其中,M∉I表示与M1异类的李群样本集合。
覆盖学习存在两种固有现象,即误判和拒识。误判是由于覆盖域存在重叠造成的。而拒识是由于未知类别样本点落在未覆盖区域造成的。针对这两种现象,本文采用以下解决方案:
(1)针对误判现象,使用如下功能函数来最终确定样本的所属类别:

(2)对于拒识现象,本文依据观测样本集中的某一类别的所有样本求解出它们各自的内均值。然后求解拒识样本点到类别内均值的核距离,距离最小的类别即是该拒识样本点的类别。其中,内均值定义为如下形式:

其中n表示该类样本的个数。
根据上面的论述,很容易得到多李群核覆盖学习算法。多李群核覆盖学习算法的具体步骤如下:
输入:样本集U,一共s个类别。
输出:每个类别的覆盖集合Ci,i=1,2,…,s。
步骤1将训练样本集U,利用协方差矩阵映射为李群样本集X,且样本集共分为s个类别,即X= {X1,X2,…,Xs}。
步骤2在样本集Xi(i=1,2,…,s)中构造覆盖区域。依次取每个样本作为中心,利用式(7)求解每个样本的覆盖邻域θ。
步骤3删除样本集Xi中被覆盖的同类样本点,并将加入到覆盖集合Ci中。
步骤4重复上述步骤,直到所有样本都被覆盖。
假设对样本进行m分块的时间是常量t,而每块提取d维特征的时间开销为dm,则n样本所需的时间开销为n(t+mdm)。设样本共有s个类别,步骤2、步骤3中需要求解某一样本与异类样本之间的两两测地线距离,从而最大时间开销为(n′)2,其中n′≤n。故算法的时间复杂度为:

因此该算法的时间复杂度为O(n2)。
4 实验结果及分析
本文将通过两个实验验证多李群核覆盖学习算法的性能,并与多连通李群覆盖学习算法进行比较。两个实验采用的数据集都是MNIST手写体数据集。第一个实验选择相似性较大的样本和相异性较大的样本分别做了两个两类样本分类实验;第二个实验就MNIST数据集上的多类样本进行实验。
4.1 MNIST手写体数据集上两类样本的分类
本实验采用MNIST数据集,该数据集中的样本是一个二维图像,具体实例如图2所示。每个手写体数字都是28×28像素的灰度图像。利用2.2节的方法可以将图像转换为李群样本。实验中,选取数字6和9作为训练集和测试集,显然数字6和9具有很强的相似性。分别从6、9手写体数字测试集中随机选取100个样本作为实验测试集,然后依次分别从6、9手写体数字训练集随机抽取50、80、110、140、170、200个作为训练集。
由于李群高斯核函数中存在超参数γ,进行实验之前需确定超参数γ的取值。本文在确定的训练集和测试集上,给超参数γ一个初始值0.015,然后以步长10倍的关系进行缩小下降。实验结果如图3所示。从图中可以看到,γ的取值为0.015×10-14时最好,因此实验中选取该值作为超参数γ的取值。

Fig.2 Data of experiments图2 实验数据

Fig.3 Value of parameterλ图3 参数λ的取值
两类样本6和9的分类实验结果如图4所示。其中,MLGKCLA是本文方法的结果,而MCLCLA是多连通李群覆盖学习算法的实验结果。
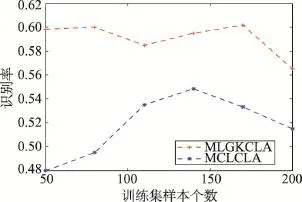
Fig.4 Result of two algorithms on 6 and 9图4 数字6和9的分类结果
选择手写体数字7和8,再次做了实验。该实验中的数字7和8具有很大的差异性。同样,分别从7和8的测试集中随机抽取100个样本组成包含200个样本的测试集。然后,分别从7和8的训练集中随机抽取50、80、110、140、130、200个样本构成相应的训练集。然后,利用多李群核覆盖学习算法和多连通李群覆盖学习算法对其进行分类,分类结果如图5所示。
在进行农产品创新之后,农家乐也是产业链中必不可少的,首先,农家乐的出现不仅给农民增添了收入,也是这一产业中的基本特征,也是在旅游业当中农民参与现代化利益的有效途径,实现了农村与城市间的贫富差距减少,但是在这之间对农家乐也需要创新,农家乐可以与旅游业更好的结合,实现第一、第三产业的相互促进,更多的是能在经济发展的同时也不会损害了环境上的利益。
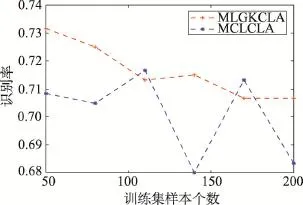
Fig.5 Result of two algorithms on 7 and 8图5 数字7和8的分类结果
对比图4和图5可知,在小样本训练集上,本文算法性能较好。同时,当样本具有很强的相似性时,多李群核覆盖学习算法能够进行较好的分类。而且,本文算法更具有稳定性。
4.2 MNIST手写体数据集上多类样本的分类
从手写体数据集中选择0、1、2手写体数字作为训练集以及对应的测试集。从0、1、2手写体数字的测试集中分别随机抽取100个作为本实验的测试集。同时,从0、1、2训练集分别依次取50、80、110、140、170、200个数据作为训练集。图6显示了两种算法的分类性能。
从图6中两个算法的比较来看,在随样本个数的增加而随机抽取一定数量的样本下,两个李群算法的变化趋势是相同的,即同升同降。但是,MLGKCLA算法比MCLCLA算法更稳定,且具有更高的分类准确率。利用协方差矩阵来提取图像的特征,考虑样本特征在李群中的空间结构,对图像的分类具有一定的优势。

Fig.6 Result of two algorithms on multi-class objects图6 两个算法在多类对象上的分类结果
5 结论与展望
本文将李群和核函数相结合提出了多李群核覆盖学习算法。该算法在小样本训练集及相似性较高样本分类中,具有一定的分类性能。但是,实验中发现一些问题,比如图5中存在两个特殊点。下一步对其进行深入研究,以发现是什么原因造成这种现象,以求对其进行改进。同时,对于覆盖学习来说,能不能利用生成模型,通过生成一些有效点来增加某类别的覆盖范围以减少拒识现象,或者细化其覆盖范围以减少误判呢,这些也是需要进一步研究的。而利用核函数思想,怎么更进一步利用核的相似性判定,来使得形成的覆盖域更具有可分性,期望接下来对其进行研究,以获得一定的解决方法。
[1]Li Fanzhang,Zhang Li,Yang Jiwen,et al.Lie Group machine learning[M].Hefei:University of Science and Technology of China Press,2013.
[2]Gao Cong,Li Fanzhang.Lie group means learning algorithm[J].Pattern Recognition and Artificial Intelligence, 2012,25(6):900-908.
[3]Xu Hanxiang,Li Fanzhang.Semi-supervised learning algorithm based on Lie group[C]//Proceedings of the 2009 WRI Global Congress on Intelligent Systems,Xiamen,China,May 19-21,2009.Washington:IEEE Computer Society,2009:573-577.
[4]He Wenhui,Li Fanzhang.Research on Lie group deep structure learning algorithm[J].Journal of Frontiers of Computer Science and Technology,2010,4(7):646-653.
[5]Ge Huilin,Zhu Zhiyu.Tracking video target via particle filtering on the Lie group normal distribution[C]//2013 32nd Chinese Control Conference,Jul 26-28,2013:904-908.
[6]Terze Z,Müller A,Zlatar D.Lie-group integration method for constrained multibody systems in state space[J].Multibody System Dynamics,2014,33(33):1-33.
[7]Bourmaud G,Megret R,Giremus A,et al.Global motion estimation from relative measurements using iterated extended Kalman filter on matrix Lie groups[C]//Proceedings of the 2014 IEEE International Conference on Image Processing, Paris,Oct 27-30,2014.Piscataway,USA:IEEE,2014:354-356.
[8]Yan Chen,Li Fanzhang,Zou Peng.Multiply connected Lie group covering learning algorithm for image classification[J]. Journal of Frontiers of Computer Science and Technology, 2014,8(9):1101-1112.
[9]Yan Chen,Li Fanzhang.Path optimization algorithms for covering learning[J].Journal of Software,2015,26(11): 2781-2794.
[10]Sagle A A,Walde R E.Introduction to Lie groups and Lie algebras[J].Siam Review,2010,8(1):11-46.
[11]Gallier J.Basics of classical Lie groups:the exponential map,Lie groups and Lie algebra[M]//Geometric Methods andApplications.New York:Springer,2011:459-528.
[12]Gallier J,Gallier C J.Notes on differential geometry and Lie groups[DB/OL].(2016)[2016-04-08].http://www.cis.upenn. edu/~jean/gbooks/manif.html.
[13]Politis D.High-dimensional autocovariance matrices and optimal linear prediction[J].Electronic Journal of Statistics, 2015,9:753-788.
[14]Yeh A B,Lin D K J,Mcgrath R N.Multivariate control charts for monitoring covariance matrix:a review[J].Quality Technology&Quantitative Management,2016(4):415-436.
[15]Förstner W,Moonen B.A metric for covariance matrices[M]//Geodesy-The Challenge of the 3rd Millennium.Berlin,Heidelberg:Springer,2000:299-309.
[16]Müller K R,Mika S,Tsch G,et al.An introduction to kernelbased learning algorithms[J].IEEE Transactions on Neural Networks,2001,12(2):181-201.
[17]Zhang Yingwei.Enhanced statistical analysis of nonlinear processes using KPCA,KICA and SVM[J].Chemical Engineering Science,2009,64(5):801-811.
[18]Bowman A W.An alternative method of cross-validation for the smoothing of density estimate[J].Biometrika,2015, 71(2):353-360.
[19]Agrachev A,Lee P W Y.Generalized Ricci curvature bounds for three dimensional contact subriemannian manifolds[J]. MathematischeAnnalen,2014,360(1/2):209-253.
[20]Yang Meng,Zhang Lei,Shiu S C K,et al.Robust kernel representation with statistical local features for face recognition[J].IEEE Transactions on Neural Networks&Learning Systems,2013,24(6):900-912. [21]Fletcher P T,Lu C,Joshi S.Statistics of shape via principal geodesic analysis on Lie groups[C]//Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Madison,USA,Jun 18-20,2003. Washington:IEEE Computer Society,2003:95.
附中文参考文献:
[1]李凡长,张莉,杨季文,等.李群机器学习[M].合肥:中国科技大学出版社,2013.
[2]高聪,李凡长.李群均值学习算法[J].模式识别与人工智能,2012,25(6):900-908.
[4]何文慧,李凡长.李群深层结构学习算法研究[J].计算机科学与探索,2010,4(7):646-653.
[8]严晨,李凡长,邹鹏.多连通李群覆盖学习算法在图像分类上的应用[J].计算机科学与探索,2014,8(9):1101-1112.
[9]严晨,李凡长.覆盖学习的道路优化算法[J].软件学报, 2015,26(11):2781-2794.

WU Luhui was born in 1990.He is an M.S.candidate at College of Computer Science and Technology,Soochow University.His research interest is Lie group machine learning.
吴鲁辉(1990—),男,安徽阜阳人,苏州大学计算机科学与技术学院硕士研究生,主要研究领域为李群机器学习。

LI Fanzhang was born in 1964.He received the M.S.degree in computer science and technology from University of Science and Technology of China in 1995.Now he is a professor and Ph.D.supervisor at Soochow University. His research interests include artificial intelligence and machine learning,etc.
李凡长(1964—),男,云南宣威人,1995年于中国科技大学获得硕士学位,现为苏州大学教授、博士生导师,主要研究领域为人工智能,机器学习等。
Multiply Lie Group Kernel Covering LearningAlgorithm for Image Classification
WU Luhui,LI Fanzhang+
College of Computer Science and Technology,Soochow University,Suzhou,Jiangsu 215000,China
+Corresponding author:E-mail:lfzh@suda.edu.cn
Lie group not only has algebraic structures,but also has manifold structures.Data are mapped to multiply Lie group,according to the track ralation of Lie group samples on the manifold,these tracks which are homotopic can be covered.So,these covering areas can present the category information.This paper proposes a new covering algorithm called multiply Lie group kernel covering learning algorithm that uses kernel function to make the covering area have more divisibility and the edge of covering area smooth.The experimental results on the MNIST datasets show that the proposed algorithm has better classification performance with comparison to the other algorithm called multiply connected Lie group covering learning algorithm.
Lie group;manifold;covering learning algorithm;kernel function
10.3778/j.issn.1673-9418.1605035
A
TP181
Received 2016-05,Accepted 2016-07.
CNKI网络优先出版:2016-07-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160701.1646.002.html
