DNA芯片一类特殊0-1规划问题的计算模型

朱建鹏，殷志祥

(安徽理工大学理学院，安徽 淮南 232001)



DNA芯片一类特殊0-1规划问题的计算模型

朱建鹏，殷志祥

(安徽理工大学理学院，安徽 淮南 232001)

作为整数规划问题的特殊情形，0-1规划问题是运筹学中应用广泛的问题之一，具有极大的研究价值。生物芯片技术与DNA计算相结合的产物DNA芯片在DNA计算模型中有着独特的优势。基于DNA芯片和DNA计算，针对一类特殊的0-1规划问题提出了DNA计算模型。该模型易实现操作过程自动化，具有操作简单、高信息量的优点。

整数规划问题；0-1规划问题；DNA计算；DNA芯片

自从Adleman博士以DNA序列为载体，利用分子生物学技术解决了有向Hamilton问题[1]以来，DNA计算成为新的研究领域，凭借其高度并行性、高存储、低耗能等优势而备受关注。1995年，文献[2]在Adleman的试验基础上，通过构造接触网络图G解决了SAT问题，文献[3]提出了利用质粒DNA分子来解决SAT问题，随后解决了最大独立集问题，文献[4]描述了一种基于自装配单链核酸链网络的空间图灵机。2000年，Sakamoto等利用DNA自组装形成的发夹结构解决了3-SAT问题。2001年，Benenson基于分子生物的可编程和自治计算机器的研究，开发了半自动化试管型DNA计算机。次年，文献[5]给出并基于半自动化自组装DNA计算模型解决了含20个变元的3-SAT问题。

作为整数规划的特殊形式，0-1规划问题是运筹学中的一个重要问题，具有广泛应用，如指派问题、选地问题等均可归为此类规划。解决该问题的算法很多，如穷举法，隐枚举法，分支定界法等，但目前为止还没有好的算法来完全解决该问题。2003年，Yin首次给出了一种基于荧光标记的方法，利用DNA计算解决了一类特殊0-1规划问题[6]，即指派问题的推广。文献[7]412-415等采用DNA芯片技术解决了简单0-1规划问题，文献[8]基于DNA芯片计算模型解决了组合数学中一类经典问题——全错位排列问题。随后，有不少学者对于其他类型的0-1规划问题，先后提出了相应的DNA计算模型[9-10]。

生物芯片在DNA计算领域的应用及其显著优点表明DNA芯片技术有望成为新型生物计算的芯片，在一定程度上弥补了以前DNA计算模型的不足。本文基于DNA芯片，利用荧光标记对一类特殊0-1规划问题提出了新的计算模型。该模型易实现操作过程自动化，具有操作简单、高信息量的优点。

1 一类特殊0-1规划问题的形式转换

0-1规划问题是整数规划问题的特殊情形，其变量仅取值0或1。其一般形式如下

max(min)u=c1x1+c2x2+…+cnxn

(1)

(2)

基于DNA计算，本文给出上式(2)中aij=-1、 0 或 1，bi为任意整数时的0-1规划问题的一种新的求解算法。对(2)中的任意约束方程，若bi≤0，则可通过对方程两边同时乘以-1使得bi≥0。故我们假定bi≥0，i=1，2，…，m。

对于(2)中任意约束方程

ai1x1+ai2x2+…+ainxn≤(=，≥)bi

(3)

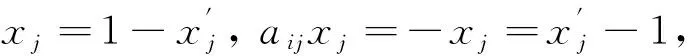
(4)

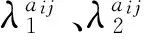
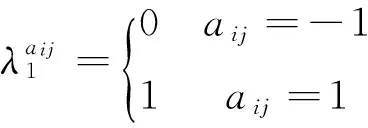
(5)

进而实现对(2)的变形，得到如下方程组

(6)

为便于理解，下面以具体的例子来解释和描述上述变形过程

min u=2x+3y-z

(7)

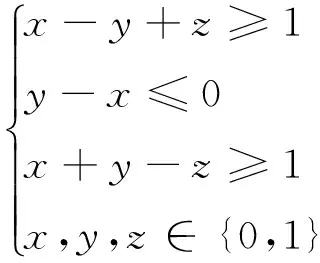
(8)

同理，第二个约束方程y-x≤0变为x′+y≤1；第三个约束方程x+y-z≥1变为x+y+z′≥2。于是，方程组(8)变形为

(9)

综上所述，对于式(2)中aij=-1、0或1，bi为任意整数的特殊0-1规划问题，可利用上述方法变形为0-1规划问题的一般形式。此形式转换的方法是新算法得以实施的前提与基础。

2 计算模型

2.1 基本算法

对于一个含有n个变量x1，x2，…，xn和m个方程的方程组，其算法的步骤如下：

步骤1 生成给定问题的变量取值为0或1的所有可能组合；

步骤2 利用每一约束方程筛选可行解；

步骤3 生成剩余解；

步骤4 对步骤2、3重复(m-1)次，即可得到问题的所有可行解；

步骤5 比较各可行解对应的目标函数值，最终得到最优解。

2.2 生物算法

步骤1 制作代表给定问题的变量的DNA链及其补链；

步骤2 根据碱基互补配对原则，将DNA链杂交，获得代表给定问题的变量取值为0或1的所有组合解的DNA数据库；

步骤3 用一定的生物方法对结果标记，使其可以检测到判断满足某约束条件的组合；

步骤4 根据约束方程筛选出所有满足该方程的组合；

步骤5 重复步骤4，筛选出所有满足各约束方程的组合，从而确定给定问题的所有可行解；

步骤6 求出各可行解对应的目标函数值，比较大小确定最优解。

基本思想：将0-1规划问题的变量映射为DNA链，将其按特定的排列方式固定在可寻址的DNA芯片上。通过加入代表变量的DNA链的互补链，DNA分子按照碱基互补配对原则杂交，生成给定问题的变量取值为0或1的所有解。在一定条件下进行反应，通过荧光扫描仪扫描反应标记结果及计算机分析可得到最优解。

2.3 编码及操作

步骤1 分为两步：

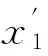
步骤2 将一定量的第三、四、五、六组的DNA链与步骤1表面的DNA矩阵在严格条件下杂交，形成包含该问题所有可能解的DNA数据库。杂交后在适当条件下用缓冲液清洗掉未杂交上的DNA链。

步骤3 由于步骤1中已经对第四、六组DNA链进行了荧光标记，所以若某DNA链发出荧光，则表示其对应的变量取值为1，否则取值为0。据此可在步骤4中找出可行解。

步骤4 利用激光共聚焦显微镜获取反应后DNA矩阵的图像信息并进行分析，保留满足约束方程的可行解。

步骤5 重复步骤4 (由于对DNA矩阵杂交后图像信息的一次获取即可对所有约束方程进行分析，故没必要再次获取图像信息)，筛选满足约束方程的可行解。

步骤6 计算各可行解所对应的目标函数值，经过比较找到问题的最优解。

现实性分析：由于DNA分子数量和种类的无穷性，合成2n种有较大差异的短的寡聚核苷酸是易实现的，因此可用ABI 392合成仪合成所需的不同的DNA链。其次，现有的荧光剂种类繁多，如二苯乙烯型、香豆素型等，而本算法中不论变量数n为何值，只需一种荧光剂即可。最后，DNA芯片技术有了重大进展，制备可寻址的DNA芯片也是可以实现的。然后利用激光共聚焦显微镜获取反应后DNA矩阵的图像信息并进行分析，保留满足约束方程的可行解即可。

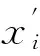
3 算法实例分析

下面以一个简单的特殊0-1规划问题为例对算法加以分析

min u=2x+3y-z

(7)

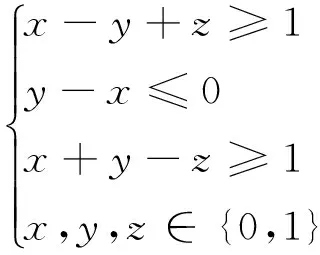
(8)

令x=1-x′，y=1-y′，z=1-z′，则(8)式变为

(9)

步骤1 分为两步：

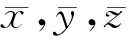
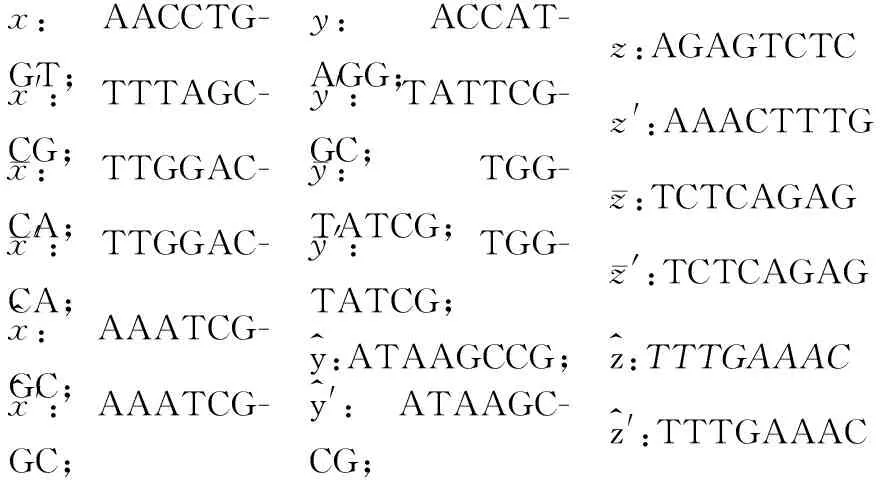
x:AACCTG-GT;y:ACCAT-AGG;z:AGAGTCTCx':TTTAGC-CG;y':TATTCG-GC;z':AAACTTTGx:TTGGAC-CA;y:TGG-TATCG;z:TCTCAGAGx':TTGGAC-CA;y':TGG-TATCG;z':TCTCAGAGx^:AAATCG-GC;y^:ATAAGCCG;z^:TTTGAAACx^':AAATCG-GC;y^':ATAAGC-CG;z^':TTTGAAAC

图1 各个变量的寡聚核苷酸编码示意图

② 将第一、二组的DNA片段的5′端进行巯基修饰，从上到下按照x，x′，y，y′，z，z′的顺序固定在芯片表面，重复排列为DNA矩阵，点样组数大于8(见图2)。

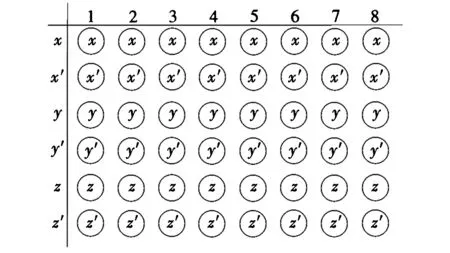
图2 芯片点样矩阵

步骤2 将第四、六组的DNA片段的5′端进行荧光标记，标记物为荧光黄(FAM)。将一定量的第三、四、五、六组的DNA链混合均匀，在合适的条件下(如42℃，6h)与DNA芯片矩阵杂交，产生满足给定问题的所有可能解。充分反应后在严格条件下用缓冲液清洗掉未杂交上的DNA链(见图3，填充部分表示发光)。

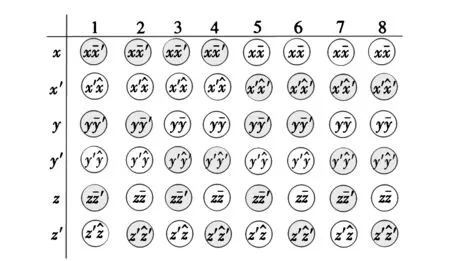
图3 杂交后的所有可行解

步骤4 利用激光共聚焦显微镜观察反应后的DNA芯片，记录并分析结果。对于第一个约束方程x+y′+z≥2，只需观察变量x、y′、z所在的第1、4、5行对应的各列发光情况即可。显然，变量x、y′、z之和不少于2，即与x、y′、z杂交发出的荧光数目之和不少于2的列满足该方程，即第1、3、4、7列为该方程的可行解。

步骤5 重复步骤4，由图3不难得出以下结论：对于第二个约束方程x′+y≤1， 第1、 2、 3、 4、7、8列为该方程的可行解； 对于第三个约束方程x+y+z′≥2，第1、2、4、6列为该方程的可行解。从而满足约束方程组的可行解为第1、4列，即对应的编码变量组合分别为(1，1，1，)、(1，0，0)。

步骤6 计算得到可行解(1，1，1，)、(1，0，0)对应的目标函数值分别为4、0，因此，目标函数的最优解为(1，0，0)，其最小值为2。

4 结论

本文对一类特殊0-1规划问题给出了DNA计算模型，通过变量替换使得所有变量的系数变为0或1，转化为简单的0-1规划问题。该模型将问题的变量映射为寡聚核苷酸链，采用DNA芯片技术制作可寻址的DNA变量矩阵。DNA片段遵循碱基互补配对原则进行杂交，生成给定问题的DNA数据库，利用激光共聚焦显微镜观察杂交矩阵上的荧光信息来筛选可行解，最终求出最优解。该模型展示了DNA芯片在DNA计算领域的独特优势，操作简单可行，并行性高，能够有效避免实验操作及人为因素对计算结果造成的误差，使计算过程的自动化成为可能，大大提高了计算效率和可行解的准确性。随着分子生物技术和DNA技术的进一步结合与发展，DNA芯片的应用将更加广泛，其研究价值与日俱增。相信未来DNA芯片技术的逐渐成熟，将对DNA计算领域产生积极的影响。

[1] ADLEMAN L M.Moleeular Computation of Solutions to Combinatorial Problems[J]. Seienee， 1994(266)： 1 021-1 024.

[2] LIPTON，R J.DNA Solution of Hard Computation Problem.Seienee，1995(268)：583-585.

[3] HEAD T，ROZENBERG G，BLADERGROEN R S，et al.Computing with DNA by Operating on Plasmids[J]. Biosystems，2000，57：87-93.

[4] ROWEIS S， WINFREE E， BURGOYNE R， et al. A Stieker-based Model for DNA Computation[J]. Comput.Biol.，1998，5(4)：615-629.

[5] BRAIEH R S.Solution of a 20-variable 3-SAT Problem on a DNA computer[J].Scienee，296：499-502.

[6] 殷志祥，张凤月，许进.0-1规划问题的DNA计算模型[J].电子与信息学报，2003，25(1)：62-66.

[7] 张凤月，殷志祥，许进. DNA芯片在0-1规划问题中的应用[J]. 生物化学与生物物理进展. 2003，30(3)：412-415.

[8] 孙侠，殷志祥，李勇，等. 全错位排列问题的基于芯片的DNA计算模型[J]. 大学数学， 2010，26(5)：79-82.

[9] 王雷，林亚平，李智勇. 一类特殊整数规划问题的DNA计算[J]. 计算机研究与发展，2005，42(8)： 1 431-1 437.

[10] 殷志祥，石晓龙，徐涛，等.0-1整数规划问题的半自动DNA计算模型[J].生物信息学，2006，4(3)：113-116.

[11] 王雷，林亚平. DNA计算在整数规划问题中的应用[J]. 计算机研究与发展，2005，27(5)：814-818.

[12] 胡宇舟，王雷，顾学道. 有界整数规划问题的DNA计算[J]. 计算机应用，2008，28(z1)： 18-24.

[13] 杨静，殷志祥. 基于抗原中介三链DNA结构的0-1整数规划[J]. 计算机工程与应用， 2008，44(2)：76-79.

[14] 任晓玲，白雪，刘希玉. 基于三链DNA结构的0-1整数规划改进研究[J]. 计算机应用研究， 2013，30(1)：56-59.

[15] 殷志祥，许进.分子信标芯片计算在0-1整数规划问题中的应用[J].生物数学学报，2007，22(3)：559-564.[16] 池晓菲，舒庆尧. 生物芯片技术的原理与应用[J]. 专论与综述， 2001，23(4)：370-374.

[17] 张旭，杨承，黄成军，等. 主动式生物芯片技术[J]. 微电子学， 2003，33(4)：324-327.

[18] 殷志祥. 图与组合优化中的DNA计算模型[M]. 北京：科学出版社， 2004.

[19] 周金凤. DNA计算在求解NP-完全问题的应用[J]. 科技视界，2012，2(35)：236-238.

[20] 李肯立，罗兴，吴帆，等. 基于自组装模型的最大团问题DNA计算算法[J]. 计算机研究与发展，2013，50(3)： 666-675.

[21] 周炎涛，李肯立，罗兴，等. 一种基于DNA自组装模型求解最大团问题的算法[J]. 湖南大学学报(自然科学版)， 2012，39(9)： 39-44.

(责任编辑：李 丽)

Computing Model Based on DNA Chip for Category of Special 0-1 Planning Problem

ZHU Jian-peng，YIN Zhi-xiang

(School of Science， Anhui University of Science and Technology， Huainan Anhui 232001，China)

As a special situation of integer planning problem，0-1 planning problem is widely applied in operational research and has great research value. DNA chip，a product of the combination of bio-chip technology and DNA computing，has unique advantage in the DNA computing. On the basis of the DNA chip and DNA computing，a new DNA computing model is proposed to solve a category of special 0-1 planning problem. The model is easy to realize the automatic operation process，and possesses the advantages of simple operation and high amount of information.

integer planning problem；0-1 planning problem；DNA computing；DNA chip

2016-04-13

国家自然科学基金资助项目(61170172)

朱建鹏(1991-)，男，河南新密人，在读硕士，研究方向：图论与DNA计算。

TP301

A

1672-1098(2016)05-0025-05