基于谐响应的弹性悬臂梁裂纹识别分析
2016-12-17刘文光郭隆清贺红林
刘文光,颜 龙,郭隆清,贺红林
(南昌航空大学 航空制造工程学院,南昌 330063)
基于谐响应的弹性悬臂梁裂纹识别分析
刘文光,颜 龙,郭隆清,贺红林
(南昌航空大学 航空制造工程学院,南昌 330063)
针对弹性悬臂梁的裂纹识别问题,探讨了谐响应分析在含裂纹梁损伤识别中的应用。首先结合连续介质弹性梁动力学方程和有限元方法,建立了含裂纹梁的受迫振动方程。然后,基于Abaqus平台建立了若干种含V型表面裂纹的悬臂梁有限元模型,在此基础上通过施加外部激励进行谐响应理论分析。最后,探讨了裂纹几何参数和加载位置对谐振频率及谐响应幅值的影响。结果表明,裂纹深度、裂纹位置、裂纹数量以及加载位置对谐响应变化规律有明显影响,为悬臂梁的裂纹识别提供了思路。
谐响应;裂纹;悬臂梁;参数识别
0 引言
梁是工程结构的基本单元,大量应用于航空航天等领域,如飞机的机翼、发动机的叶片、直升机的旋翼、导弹的弹体等。而振动是飞行器服役过程中必须承受的载荷形式之一,它贯穿于飞行器服役过程的各个阶段。当外部振动载荷频率与梁的固有频率一致或接近时,梁不可避免地会产生共振问题。在共振环境下,梁结构很可能产生裂纹,甚至发生振动断裂。为了提高工程梁的安全可靠性,研究梁裂纹的识别方法显得尤为重要。
基于振动的损伤识别方法,其原理大多数是通过振动试验得到系统的动力参数,然后比较系统损伤前后动力参数的变化规律,构造损伤指针对系统进行损伤识别。最常使用的动力参数有,固有频率、振型及振型曲率、频响函数以及模态应变能等,其中固有频率是最基本的振动参数。早在1968年,Lifshitz等就率先提出通过对比结构损伤前后固有频率的变化来识别结构损伤[1]。随后20世纪70年代,Cawley等利用固有频率进行损伤识别研究时发现,单损伤结构在损伤前后任意两阶固有频率的比值只与损伤发生的位置有关[2]。之后,Cerri等通过比较试验固有频率与解析固有频率的不同,求得了损伤位置[3];张兆德等通过分析两次实测固有频率的变化规律,初步定位了海洋平台的损伤[4];莫淑华等分析含损伤的复合材料层合悬臂梁固有频率时发现,利用固有频率变化率也能识别复合材料的损伤[5]。事实表明,基于固有频率的识别方法在含裂纹梁的损伤监测方面具有很大的应用价值。为此很多学者对含裂纹梁的固有频率进行了研究。吴国荣等推导了含裂纹梁的等效动力学模型,建立了含裂纹梁的固有频率方程[6];Swamidas等应用能量法和断裂力学建立张开式裂纹模型,求解了张开裂纹和无损伤梁的固有频率[7];李学平等对含多裂纹等截面梁进行振动分析,改进了梁的固有频率计算方法[8];赵迪等计算了含裂纹旋转叶片结构的固有频率[9];王振清等分析了含裂纹简支梁的振动频率随温度的变化趋势[10]。
尽管基于固有频率的含裂纹梁损伤识别理论与方法取得了很多的成果,但是多数研究者在计算含裂纹梁固有频率时候都假定裂纹处于张开状态。这显然与物理事实不符。工程中,结构裂纹的开合状态实际上会随梁的振动而变化。为此,刘文光针对裂纹的呼吸行为,研究了裂纹扩展与裂纹界面接触对弹性梁固有频率的影响[11],推导了呼吸式裂纹梁的固有频率方程[12]。之后提出了一种梁刚度随振幅变化的弹性梁固有频率计算模型,并结合等高线理论研究了一种基于固有频率的悬臂梁裂纹参数识别方法。结果表明,只要能准确地求得梁的固有频率,就能够较为理想的识别出裂纹所在的位置和裂纹的相对深度;但存在的问题是,梁的低阶固有频率对裂纹位置和深度不够敏感,需要精度极高的传感设备方能精确测取,极大地增加了裂纹识别的成本。
本研究拟通过设计含不同裂纹损伤弹性梁的有限元模型,在谐响应分析的基础上,探讨裂纹参数与响应幅值、谐振频率之间的内在联系,为基于固有频率的裂纹识别研究提供新的思路。
1 基本理论
为方便起见,取Euler-Bernoulli梁为对象,即梁在变形前垂直于梁中心线的平面,在变形后依然垂直于梁的中心线,这种假设忽略了梁的剪切变形和截面绕中性轴转动惯量的影响。
1.1 连续介质弹性梁的自由振动控制方程:
如图1所示为一等截面的均质直弹性梁,其弯曲自由振动微分方程为[13]:
(1)
式中:t为时间,w为x处的横向位移,S为x处的梁横截面积,I为截面关于中性轴的惯性矩,E为材料的弹性模量,ρ为质量密度。

图1 等截面的均质直弹性梁
假设梁的横向固有振动为
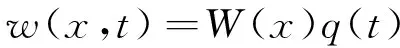
(2)
将式(2)代入式(1),整理得
(3)
式中,W(4)(x)表示W(x)对x求四阶导数。
式(3)左边为关于位置x的函数,右边全部为关于时间t的函数。因为x和t是彼此独立的量,所以式子两边必定是同时等于同一常数,且非负。因此,式(3)可以分离为2个独立的常微分方程:
(4)
(5)

(6)
(7)
式中:ω为待定固有频率;ai,bj(i=1,2,3,4;j=1,2)为待定系数。其中ω和ai由梁的边界条件确定。
悬臂梁的边界条件为

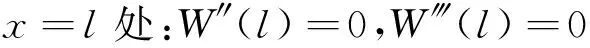
结合梁两端的边界条件,可以确定悬臂梁的固有频率ω方程为

(8)
求解该方程,可得到弹性梁的第n阶固有频率
(9)
基于方程(9)可以分析连续介质弹性悬臂梁的谐振频率,以确定梁谐响应分析的频带宽度。
1.2 含裂纹弹性梁的受迫振动控制方程
结合工程应用,通过有限元法可以建立含裂纹悬臂梁的动力学模型。忽略阻尼的影响,将Euler-Bernoulli梁转化为有限元梁模型,则无裂纹梁的受迫振动微分方程为
(10)
式中:[M]e表示梁单元质量矩阵,[Kwc]e表示梁单元刚度矩阵,{F(t)}e表示梁单元施加的外载荷向量,{q(t)}e是梁单元产生的位移向量,t是时间。
假定裂纹的存在只会对梁的刚度产生影响,而不会影响梁的质量,可得到梁模型中含裂纹单元的振动微分方程
(11)
式中:{qc(t)}e是梁模型中含裂纹单元的位移向量,[Kc]e是梁模型中含裂纹单元的刚度矩阵,并且其表达式可以写为
(12)
其中,
(13)
式中:[T]为初等变换矩阵,[C0](e)为无裂纹梁的单元柔度矩阵,[Cc](e)为裂纹单元的局部柔度矩阵,[C](e)为含裂纹梁单元的总柔度矩阵。
将含裂纹单元组装在无裂纹梁的系统中,即可得到含裂纹悬臂梁的运动微分方程
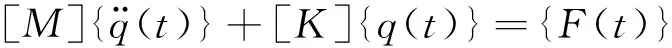
(14)
式中:[M]是组装后的整体质量矩阵,[K]为整体刚度矩阵,{F(t)}是整体外力向量,而[q]是系统的整体位移向量。
将外力向量定义为
(15)
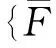
(16)

结合方程(14)~(16)可得整个含裂纹悬臂梁的运动控制微分方程:
(17)
对于一个给定的系统(即[M]和[K]确定),在外力的作用下,求解方程(17)就能得到系统的响应。
2 含裂纹悬臂梁的有限元建模
2.1 含裂纹悬臂梁的几何描述
几何建模时,设计了单裂纹、双裂纹以及不同深度裂纹多种工况模型,以探讨裂纹几何参数变化对弹性梁谐响应的影响规律,裂纹位置如图2所示,其中:a表示裂纹深度,L为梁长、b为梁宽、h为梁高,LC为裂纹距固支端的距离。为方便几何建模,假定梁为均质矩形截面梁,梁的几何尺寸L×b×h为500 mm×20 mm×29 mm,裂纹为V型表面裂纹,张开角为3°。数值计算时,取梁的弹性模量E=206.8 MPa,泊松比μ=0.3,密度ρ=7.78×103kg/m3。

图2 含裂纹悬臂梁的几何模型
2.2 有限元建模
基于Abaqus软件建立的含裂纹悬臂梁有限元网格模型如图3所示。有限元网格模型选用的是三维实体四面体单元C3D10,在对裂纹梁进行网格划分时,V型裂纹区域需要细化网格,本研究采用分割实体的网格划分技巧,即画一个小圆圈将裂纹区域围住,裂纹梁被分割成小圆圈部分和小圆圈外面的其他部分,将分隔出的这一小部分实体单独划分网格,网格的密度比其他区域的密度要大得多。划分网格时,小圆圈部分的网格密度为0.2 mm,其余部分网格密度为2 mm。

图3 含裂纹悬臂梁的有限元模型
3 裂纹对悬臂梁谐响应的影响
因为裂纹数量、裂纹深度以及裂纹位置等对悬臂梁的受迫响应具有明显影响,因此研究其内在规律对探讨基于谐响应的悬臂梁裂纹识别方法具有重要的意义。计算时,首先求取每个模型的前10阶固有频率并算平均值,并确定受迫响应分析所加载荷幅值为100 N(方向如图2所示)。然后对无损伤悬臂梁进行自由模态分析,发现第二阶弯曲模态(模态频率为96 Hz左右)对于裂纹参数变化比较敏感,所以确定第二阶模态频率为谐振频率,进而设置外部载荷频率搜索区间为0~120 Hz。
3.1 裂纹深度对谐响应的影响
假定裂纹离固支端375 mm(图2a),裂纹深度a逐渐由4 mm增加到20 mm,自由端加载。结果表明,无损伤悬臂梁的前10阶固有频率的平均值为1 322.32 Hz,且无损伤弹性梁载荷加载点的振幅在第二阶固有频率为96.56 Hz时,响应幅值达最大值4.81 mm(图4)。
从图4中可以看出,尽管裂纹深度发生变化,悬臂梁谐响应幅值最大处对应的频率都在96 Hz附近,观察局部放大图发现,谐响应曲线的峰值会随裂纹深度的增加稍稍往左移动(当裂纹深度a=4 mm时,波峰在96.5 Hz;而当a=20 mm时,波峰在95.3 Hz)。研究表明,悬臂梁的第二阶固有频率随着裂纹深度的增加而减小;而且随着裂纹深度的增加,谐响应曲线的峰值逐渐增大(当裂纹深度a=4 mm时,谐响应峰值为4.81 mm;当a=20 mm时,峰值为5.22 mm)。原因在于裂纹深度的增加导致了梁的刚度下降,使得悬臂梁的振幅增大。
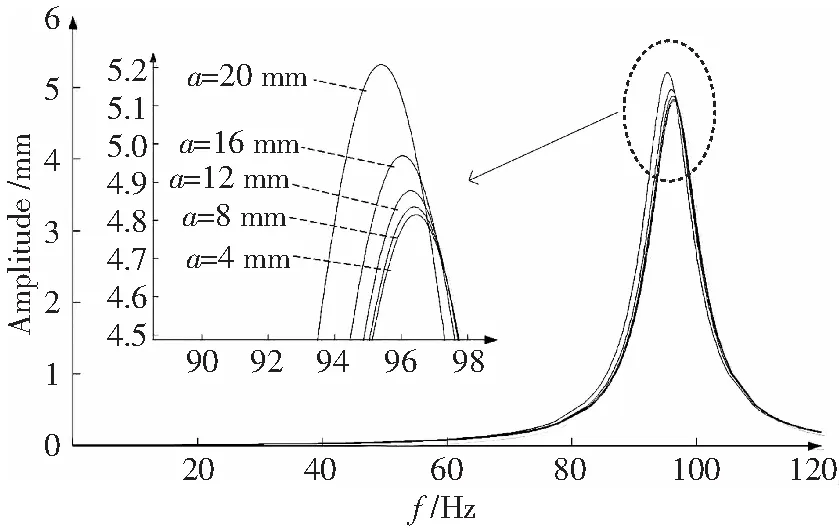
图4 裂纹深度对谐响应的影响

图5 外部激励力对谐响应的影响
谐响应规律不仅与悬臂梁模型有关,而且与加载位置有关。为探讨加载位置对谐响应曲线的影响,分析时改变外部载荷的激励位置为离固支端300 mm(图2b)。计算结果表明,谐响应幅值最大位置同样出现在96 Hz左右(图5)。分析发现,一方面谐响应幅值会随着裂纹深度的增加而增大,另一方面谐响应最大值发生位置随着裂纹的增加逐渐往左移动。结论说明,载荷位置变化不改变谐响应幅值随频率的变化规律,但是影响响应幅值对裂纹大小的敏感性。也就是说,在裂纹附近加载进行谐响应分析,因为响应幅值很小,对裂纹不甚敏感,不适于悬臂梁的裂纹识别。
3.2 裂纹位置对谐响应的影响
如图2a所示,保持裂纹深度a=4 mm不变,假定裂纹位置LC由165 mm逐渐变化到415 mm等不同位置,在自由端加载。结果如图6所示,随着裂纹远离固定端(即LC增大),梁的谐振频率逐渐增大,使得谐响应曲线图的波峰逐渐往右移动,且谐响应幅值逐渐减小。
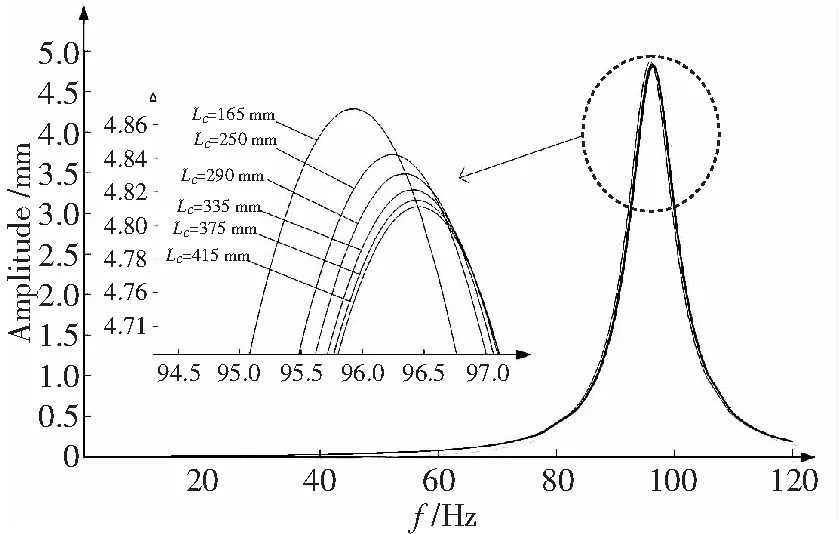
图6 裂纹位置对谐响应的影响
3.3 裂纹数量对谐响应的影响
为讨论裂纹数量对谐响应规律的影响,在梁表面设置2处裂纹,分别位于LC1=250 mm和LC2=375 mm,裂纹深度a逐渐由4 mm变化到20 mm,在自由端加载。谐响应计算结果如图7、表1所示。结果表明,随着裂纹深度变化,含双裂纹悬臂梁的谐响应幅值所对应的谐振频率在很大区间内变化。裂纹深度增加,谐振频率的位置往左移动,固有频率由96.3 Hz逐渐减小到85.5 Hz;此外,除了对应的谐振频率改变外,响应最大值也发生了改变,随着裂纹深度增加,响应幅值由4.84 mm增大到7.41 mm。研究结论显示,随着裂纹深度增加,双裂纹悬臂梁的谐振频率、谐响应幅值敏感性增加明显。

图7 裂纹数量对谐响应的影响
进一步比较图4、图7发现,不管是双裂纹还是单裂纹的悬臂梁,当裂纹深度由4 mm增加到20 mm时,其谐振频率值都会随着裂纹深度的增加而减小,谐响应幅值随着裂纹深度的增加而增大。而对于不同裂纹数量的悬臂梁,这种影响规律有一定差异,比如,含双裂纹悬臂梁的谐振频率并不总是在96 Hz附近,其变化范围较大,基于这个规律,可用于识别悬臂梁是否含有单裂纹或者双裂纹。
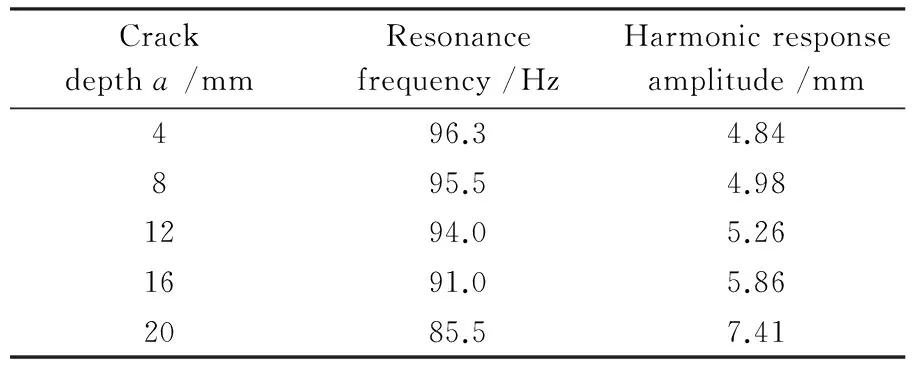
表1 不同裂纹深度的双裂纹悬臂梁谐振频率及谐响应幅值
4 结论
1)距固支端LC=375 mm的单裂纹,自由端加载,当裂纹深度由4 mm增加到20 mm时,悬臂梁的谐振频率由96.56 Hz减小至95.3 Hz,响应幅值由4.81 mm增加至5.22 mm;改变加载位置对悬臂梁的谐振频率没有影响,但是对响应幅值影响明显,当加载位置距固支端300 mm时,对应裂纹深度下的响应幅值由5 mm左右下降到1 mm左右。
2)裂纹深度4 mm的单裂纹,自由端加载,当裂纹位置LC由165 mm增加415 mm时,悬臂梁的谐振频率由95.85 Hz增加至96.49 Hz,响应幅值由4.861 mm减小至4.812 mm。
3)裂纹位置分别为LC1=250 mm、LC2=375 mm的双裂纹,自由端加载,当裂纹深度由4 mm增加到20 mm,悬臂梁的谐振频率由96.3 Hz逐渐减小至85.5 Hz,响应幅值由4.84 mm逐渐增加至7.41 mm。
[1] Lifshitz J M, Rotem A. Determination of reinforcement unbonding of composites by a vibration technique[J]. Journal of Composite Materials,1969,3(3):412-423.
[2] Cawley P, Adams R D. The location of defects in structures from measurements of natural frequencies[J]. Journal of Strain Analysis for Engineering Design,1979,14(2):49-57.
[3] Cerri M N, Vestroni F. Detection of damage in beams subjected to diffused cracking[J]. Journal of Sound and Vibration,2000,234(2):259-276.
[4] 张兆德,王德禹. 基于固有频率的海洋平台损伤检测方法的改进[J]. 海洋工程,2004,22(3):9-13.
[5] 莫淑华,王春艳,潘利剑. 基于固有频率改变率的复合材料层合结构损伤定位研究[J]. 材料科学与工艺,2008,16(2):274-277.
[6] 吴国荣. 含裂纹梁自由振动分析[J]. 噪声与振动控制,2008,11(5):31-34.
[7] Swamidas A S J, Seshadri R, Yang X. Identification of cracking in beam structures using timoshenko and euler formulations[J]. Journal of Engineering Mechanics,2004,130(11):1297-1308.
[8] 李学平,余志武. 含多处裂纹梁的振动分析[J]. 应用力学学报,2007,24(1):66-68.
[9] 赵迪,尚新春. 含裂纹旋转叶片结构的振动特征分析[J]. 武汉大学学报:工学版,2011,44(4):487-491.
[10] 王振清,刘兵,韩玉来. 高温下含裂纹铝合金梁自由振动频率分析[J]. 哈尔滨工程大学学报,2012,33(3):320-324.
[11] 刘文光,严铖,贺红林. 结构裂纹对弹性梁振动特性的影响[J]. 失效分析与预防,2013,8(5):259-263.
[12] 刘文光,陈国平. 呼吸式裂纹梁的振动疲劳裂纹扩展耦合分析[J]. 中国机械工程,2010,21(23):2798-2802.
[13] 胡海岩. 机械振动基础[M]. 北京:北京航空航天大学出版社, 2005.
Analysis on Crack Identification of an Elastic Cantilever Beam by Harmonic Response
LIU Wen-guang, YAN Long,GUO Long-qing,HE Hong-lin
(SchoolofAeronauticalManufacturingEngineering,NanchangHangkongUniversity,Nanchang330063,China)
According to the problem of crack damage in the elastic cantilever beam, a damage identification method of cracked beam was discussed by harmonic response. Combined with the elastic continuum beam dynamics and the finite element method, the forced vibration equation of the cracked beam was set up. Then several finite element models of the cantilever beam with V type crack were constructed, and the harmonic response analysis were carried out through acting external force on the models to discuss the relation of the crack parameters and the harmonic response. The impacts of loading position on the response magnitude were also discussed in the end. Results indicate that the impacts of crack depth, crack position, crack number and loading position on the change law of harmonic response are obvious, and it provides a new idea for crack identification of cantilever beam.
harmonic response; crack; cantilever beam; parameter identification
2016年4月6日
2016年5月20日
国家自然科学基金 (51565039)
刘文光(1978年-),男,博士,副教授,主要从事飞行器结构动力学与疲劳寿命预测等方面的研究。
TH212;TH213.3
A
10.3969/j.issn.1673-6214.2016.03.003
1673-6214(2016)03-0143-05
