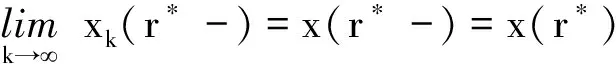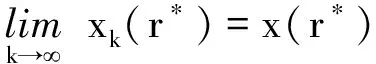Carathéodory方程解对参数的连续依赖性

李宝麟,张珍珍,张元德

(西北师范大学 数学与统计学院,甘肃 兰州 730070)



Carathéodory方程解对参数的连续依赖性

李宝麟,张珍珍,张元德

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

Carathéodory方程能转化为广义常微分方程的形式,利用广义常微分方程解对参数的连续依赖性证明了Carathéodory方程解对参数的连续依赖性定理。

Carathéodory方程;广义常微分方程;Kurzweil积分;连续依赖性

Kurzweil[1]在1957年首次提出了广义常微分方程,并对广义常微分方程进行了研究,得出了许多有用的结果。而且很多其他形式的方程都能转化为广义常微分方程,包括脉冲微分方程、测度微分方程[2]、时间轴上的动力微分方程[3]和一些其他方程等。众所周知,在适当的条件下,广义常微分方程的解关于参数具有连续依赖性[1]。研究借助广义常微分方程解关于参数的连续依赖性[4-8]得到Carathéodory方程的解对参数的连续依赖性。

考虑Carathéodory方程:

(1)

1 预备知识

首先介绍广义常微分方程与Kurzweil积分的相关理论。

定义1 函数F∶[a,b]×[a,b]→Rn在区间[a,b]上称为Kurzweil可积的[6],如果存在向量I∈Rn,对任意的ε>0,在区间[a,b]上存在正值函数δ,使得对区间[a,b]上的任何δ-精细分划D,都有

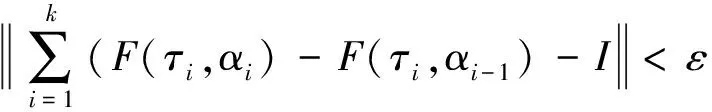
(2)

定义2 一个函数x∶[a,b]→Rn,如果对所有的s∈[a,b],有

则称函数x为广义常微分方程

(3)

的解[2]。

定义3 设函数F∶G→Rn,如果F属于函数族F(G,h,ω)[2],则对所有的(x,s2),(x,s1)∈G,有‖F(x,s2)-F(x,s1)‖≤|h(s2)-h(s1)|,

(4)

且对所有的(x,s2),(x,s1),(y,s2),(y,s1)∈G有‖F(x,s2)-F(x,s1)-F(y,s2)+F(y,s1)‖≤ ω(‖x-y‖)|h(s2)-h(s1)|,

(5)其中:h∶[a,b]→R为不减函数;ω∶[0,+)→R为连续的增函数,且ω(0)=0。

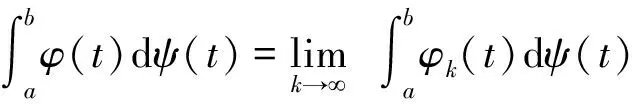
(6)

引理4 假设F∶G→Rn满足条件(4)。如果[α,β]⊂[a,b]且x:[α,β]→Rn是方程(3)的解,则对任意的s1,s2∈[α,β],不等式

‖x(s1)-x(s2)‖≤|h(s2)-h(s1)|

成立[2],其中h∶[a,b]→R为不减函数。

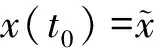
进一步,我们很自然地可以假设

(7)

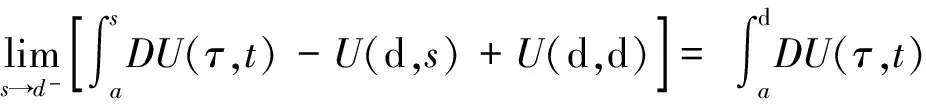
(8)

引理7 假设Fk∶G→Rn属于函数族F(G,h,ω),k=0,1,…,且对(x,t)∈G,有

(9)

成立。令xk∶[α,β]→Rn,k=1,2,…是广义常微分方程

(10)

在区间[α,β]⊂[a,b]上的解,并且使得

(11)

和(x(s),s)∈G,s∈[α,β]。则x∶[α,β]→Rn在区间[α,β]上是有界变差的并且是广义常微分方程

(12)

在区间[α,β]上的解[3]。

证明 类似于文献[2]中相关引理的证明。

2 主要结论

借助于广义常微分的方法证明Carathéodory方程的解关于参数的连续依赖性定理。

(13)

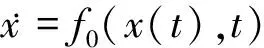
(14)

则对足够大的k∈N,方程

(15)

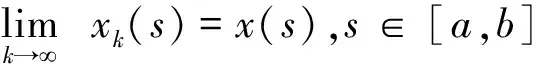
证明 首先证明Carathéodory方程能转化为广义常微分方程,令

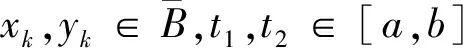
由假设可得(y,a)∈G且

因为

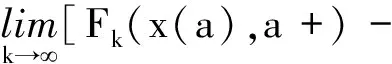
且

‖Fk(yk,a+)-Fk(x(a),a+)-Fk(yk,a)+ Fk(x(a),a)‖≤ω(‖yk- x(a)‖)(h(a+)-h(a))。

因此可得,存在k1∈N使得对k>k1有(yk,a)∈G,也就是说

(yk+Fk(yk,a+)-Fk(yk,a),a)∈G。

所以存在r>a使得,若t∈[a,r]且

‖x-(yk+Fk(yk,a+)-Fk(yk,a)‖≤ h(t)-h(t+),

则(x,t)∈G,k>k1。由引理5可得方程(10)存在解xk∶[a,r]→Rn使得xk(a)=yk,k>k1。

因此可得,对t∈[a,r]都有

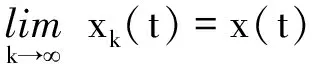
而且可以验证,和方程(10)右端的函数Fk类似,r>a的取值仅与函数h有关。

根据引理7和方程(12)的解的唯一性假设可知,若函数列xk在区间[a,r]上包含一个逐点收敛的子序列,则对t∈[a,r],这个子序列的极限一定是x(t)。进一步,再由引理4可知,区间[a,r]上的函数列xk,k>k1,在这个区间上等度有界并且一致有界变差,由引理7可知,序列xk对每个t∈[a,r]都有逐点收敛的子序列xk(t)。

上面的证明说明了这个结论在区间[a,r],r>a上成立。现在,假设这个结论在整个区间[a,b]上都不成立。由假设可知,存在r*∈(a,b)使得对于任意的r

但却在区间[a,r],r>r*上是不成立的。由引理4,有

‖xk(t2)-xk(t1)‖≤|h(t2)-h(t1)|, t1,t2∈[a,r*),

其中k∈N是足够大的。因此,xk(r*-)的极限存在,又因为方程的解x是左连续的,故有

令xk(r*)=xk(r*-),可得

这也就是说,这个定理在闭区间[a,r*]上是成立的。类似地,我们也可以用同样的方法证明这个结论在闭区间[r*,r*+Δ]上依然成立,其中Δ>0。这与原假设矛盾,即结论在整个闭区间[a,b]上是成立的。

[1] Kurzweil J.Generalized Ordinary Differential Equations and Continuous Dependence on a Parameter[J].Czechoslovak Math.J,1957,82:418-448.

[3] Slavík A.Dynamic Equations on Time Scales and Generalized Ordinary Differential Equations[J].J.Math.Anal.Appl,2012,385:534-550.

[5] 李宝麟,吕卫东.广义Carathéodory系统有界变差解的存在性[J].甘肃科学学报,2007,19(4):1-3.

[7] Halas Z.Continuous Dependence of Solutions of Generalized Linear Differential Equations on a Parameter[J].Mathematica Bohemica,2007,132(2):205-218.

[8] Krasnoselskij M A,Krein S G.On the Averaging Principle in Nonlinear Mechanics[J].Uspehi Mat.Nauk,1955,10(3):147-152.

Continuous Dependency of Solution of Carathéodory Equation on Parameter

Li Baolin,Zhang Zhenzhen,Zhang Yuande

(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,China)

Carathéodory equation can be transformed into the type of generalized ordinary differential equation,this paper uses the continuous dependency of solution of generalized ordinary differential equation to prove the continuous dependency theorem of solution of Carathéodory equation on parameter.

Carathéodory equation;Generalized ordinary differential equation;Kurzweil integration;Continuous dependency

Li Baolin,Zhang Zhenzhen,Zhang Yuande.Continuous Dependency of Solution of Carathéodory Equation on Parameter[J].Journal of Gansu Sciences,2016,28(6):1-4.[李宝麟,张珍珍,张元德.Carathéodory方程解对参数的连续依赖性[J].甘肃科学学报,2016,28(6):1-4.]

10.16468/j.cnki.issn1004-0366.2016.06.001.

2016-01-30;

2016-04-27.

国家自然科学基金项目(11061031).

李宝麟(1963-),男,甘肃天水人,博士,教授,研究方向为应用微分方程.E-mail:libl@nwnu.edu.cn.

张珍珍.E-mail:zhang151007@yeah.net.

O175.12

A

1004-0366(2016)06-0001-04