基于统计特征的轨道交通站点乘降量预测算法研究
2016-12-16牛琳博
姜 梅 牛琳博
(1. 中铁二院工程集团有限责任公司科学技术研究院 成都 610031;2. 西南交通大学交通运输与物流学院 成都 610031)
基于统计特征的轨道交通站点乘降量预测算法研究
姜 梅1牛琳博2
(1. 中铁二院工程集团有限责任公司科学技术研究院 成都 610031;2. 西南交通大学交通运输与物流学院 成都 610031)
针对现有预测方法因未考虑城市轨道交通站点乘客的随机性,致使乘降量预测精度不高的问题,提出一种基于统计特征的客流量预测方法。依据日期、时段、天气、突发事件等因素将历史数据进行分类。建立基于乘降量统计特征的分布模型,根据其预测客流的统计特征,结合随机数产生算法,产生的随机数即为客流乘降量预测值,最后结合算例予以说明,证明该模型的可行性。
轨道交通;乘降量;预测算法;统计特征;随机数产生算法
乘降量预测是确定轨道交通发车间隔、合理分配车底的前提,预测结果是制定轨道交通系统调度计划的依据。因此,乘降量预测对轨道交通的运营效能具有重要意义。
目前,对于城市内公共交通车站的乘降量预测方法很多,主要有以下两种:一类研究是基于时间序列对乘降量进行短期预测,其代表性成果有张世英[1-2]等人通过时间序列、沈家军[3]等人结合灰色预测模型预测公交站点短时乘降量;另一类研究是利用相关智能算法进行预测,代表性研究有Zijpp Van der[4]等人利用人工神经网络、张春辉[5]等人利用卡尔曼滤波法、郭士永[6]等人利用最小二乘支持向量机回归算法、刘凯[7]等人利用小波预测方法等建立的乘降量预测模型。
上述方法从不同层面完善了站点乘降量的预测研究,但仍存在一定的不足之处:1)短期客流预测模型很难建立精确的输入-输出模型;2) 对节假日等特殊客流波动规律反映不充分;3) 相关智能算法求解困难。鉴于这些不足,笔者提出一种基于统计特征的短期站点乘降量预测方法,以历史乘降量数据作为预测依据,以期达到较高的预测精度。
1 基于客流影响因素的站点乘降量类型划分
轨道交通线路上每个站点乘客的到达是随机的。乘客的乘降量会受到日期(工作日、节假日)、时段(高峰、平峰)、天气(非雨天、雨天)、客流敏感点事件(交通事故、大型集会)等因素影响。因此,为了构建统计分布模型,保证客流构建具有一致性,依据历史数据,构建统计数据集。
依据上述条件,将历史客流数据中的某一天某一时段乘降量数据进行参数化分类表达,如图1所示。
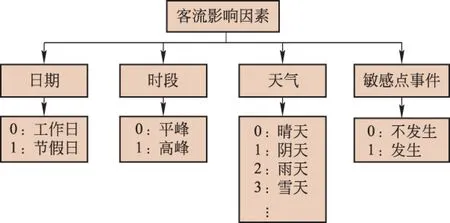
图1 历史客流数据参数化分类表达
通过上述客流分类,对所搜集的客流数据进行数据库编码存储(见图2),整理成为历史客流数据库,为本客流预测方法提供依据。
考虑到一天内不同时段乘降量的变化,对于第i站,将某一轨道交通线路在第p周中第q天客流数据的运营时间[ts,te]划分为k个等间距区间,每个区间为一个统计时段,即
[tb,te]=[ts,ts+Δt)+[ts+Δt,ts+2Δt)+
…+(ts+(k-1)Δt,te]
(1)
(2)
(3)
其中,ts为轨道交通运营开始时刻,te为轨道交通运营结束时刻,Δt为一天内统计时段长度,datap,q,Δt为某一年第p周中第q天的乘降量。
由于受经济发展的影响,客流具有动态变化性,因此,早期的数据会对短期预测的精度产生影响。为提高预测的精度,必须实现客流数据集的实时更新。将当天该站点不同时段、不同因素条件下的实时数据按不同类别存储到相应的客流数据集合,替换同类型的早期数据,完成对数据集的更新,从而为准确的预测提供数据支持。
2 基于乘降量统计特征的分布模型构建
在统计乘降量分布函数之前,需要调用历史乘降量数据。依据对已有数据的划分,判断当前的日期、天气情况、站点的预测时段、线路环境情况,对应数据的分类情况,调用已经存储的该类数据。
建立精确的短期客流预测模型,必须首先明确客流数据的统计特征,为此应采取统计学的手段对客流数据进行系统分析。
2.1 基于客流数据集的客流分布类型检验
在未受到随机因素干扰的情况下,客流服从正态分布。在实际过程中,由于受到天气、假期等随机因素的干扰,造成客流波动较大,有可能服从非正态分布。因此,引入统计学中参数与非参数检验方法。首先对客流数据采用参数检验的方法,若其检验结果不服从正态分布,采用非参数检验的方法,得出其统计特征。
2.2 基于参数统计的车站乘降量分布模型
在参数检验方法中,分布拟合χ2检验通过比较总体客流样本的实际值与理想期望的差异,判断是否服从正态分布。现对其检验过程进行详细阐述。
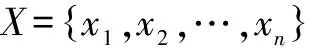
2) 再统计出总体样本X的数值出现在各个Ai(i=1,2,…,r)中的实际频数ni。
3) 在假定所选用的客流历史数据服从正态分布的前提下,总体客流样本X~N(μ,σ2),其中μ、σ2未知,用极大似然法估计确定两个未知参数。
(4)
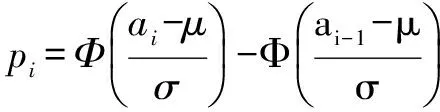
4) 考虑统计量。
(5)
式中,χ2表示实际客流乘降量结果与理想期望结果的相对差异的总和。m为被估计的分布参数的个数,其中正态分布含有2个参数,m=2。
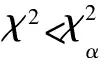
(6)
2.3 基于非参数统计的车站乘降量分布模型
客流在受到随机因素干扰的情况下,服从非正态分布,由于其分布未知,引入非参数检验方法。科尔莫格洛夫提出的Kolmogonov检验适用于除正态分布之外的其他分布,现对其进行详细阐述。
1) 客流数据样本的经验分布函数Fn(x),其假设分布函数为F(x),根据Kolmogonv定理,可得到
(7)
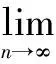
(8)
式中,k为客流数据样本X的秩。
提出假设问题H0:客流数据样本X服从非正态分布,即F(x)=F(x0),做显著性检验。
3) 给出显著性水平α,客流数据样本个数n,查Kolmogonov表得出
(9)
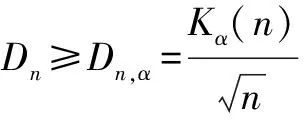
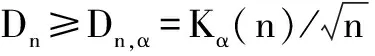
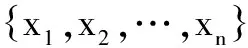
(10)
其中,xm为客流乘降量数据的中位数。
3 基于客流分布特征的车站乘降量预测
短期客流乘降量的预测结果具有随机性,结合随机数产生算法,依据其分布产生的随机数即为预测结果。对于预测服从正态分布的客流乘降量,选用线性同余法进行预测的模型如下。
采用线性递推公式[9],有
xn+1=ξxn+c(modM)
(11)
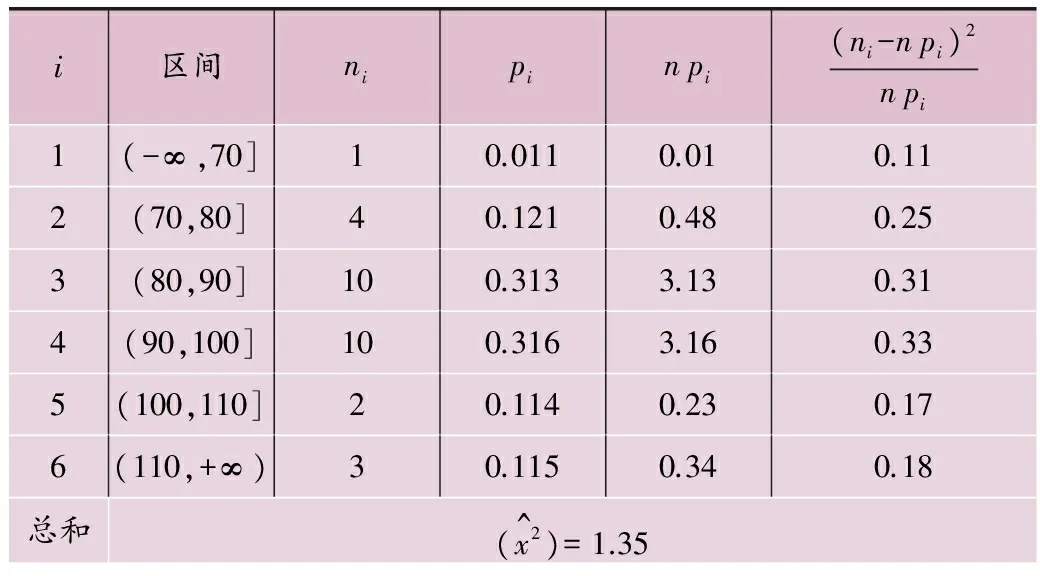
0≤xn+1 其中,ξ为乘子,c为增量,M为模。 产生客流乘降量预测随机数列 ln=xn/M (12) 其中,ln为第n个客流乘降量预测随机值,0≤ln<1。 根据上述方法得出一组服从正态分布的客流随机数:l1,l2,…,ln,将其带入下式 (13) 根据中心极限定理可知,随机变量X~N(0,1),由Y=σX+μ~N(μ,σ2),得出服从正态分布的短期客流乘降量预测结果。 假设某轨道交通线路运营时间为8:00—20:00,选取统计时段Δt=15 min,站点总数为30个。根据已知数据进行短期站点客流预测,以预测第2天的客流乘降量为例,假设其为周一并且为非节假日,由于无法预知次日运行线上是否发生突发事故,考虑其未发生敏感事故。 首先预测第1个统计时段8:00—8:15的上车人数,假设在该时段为晴天,调用数据存储中与其性质相同的数据。其结果为:90,103,62,93,88,72,81,88,121,113,72,115,92,84,92,83,84,100,99,99,91,73,92,101,90,95,92,82,88,77。应用分布拟合检验,检验上述结果是否为正态分布。将以上客流总体样本划分成6个子区间,分别为:(-∞,70],(70,80],(80,90],(90,100],(100,110],(110,+∞)。 假定客流总体样本为正态分布,其均值μ=85,方差σ2=3.22。计算过程如表1所示。 表1 样本正态分布检验过程 本文针对目前客流预测方法的不足,提出了一种基于统计特征的轨道交通站点乘降量预测方法,综合考虑日期、天气、突发事件等因素,将采集的全年历史数据进行划分并存储,引入统计分布思想,预测各个站点在相应统计时段的乘降量。其主要研究成果有:基于线路的历史乘降量数据,按照不同影响因素进行详细划分;在进行特定时段乘降量预测时,调用对应的历史乘降量数据;为了验证所调用的各组数据的统计特征,建立基于客流乘降量统计特征的分布模型,结合随机数产生算法,得出客流预测结果。本文所提出的预测方法能够克服节假日等特殊客流波动对预测结果的影响,随着轨道交通线路客流数据的累计,预测精度将得到进一步提升。针对本文成果的工程应用,统计时间间隔的划分将是下一步研究的重点。 [1] 张世英,陆晓春,李胜朋.时间序列在城市交通预测中的应用[J].天津大学学报(社会科学版),2006(5):370-372. [2] VAN D V,DOUGHERTY M,WATSON S.Combining kohonen maps with ARIMA time series models to forecast traffic flow[J].Transportation Research Part C,1996,4(5):307-318. [3] 沈家军,王炜,陈峻.基于灰色马尔可夫模型的近期公交客流量预测[J].公路交通科技,2007,24(9):120-123. [4] VAN DER ZIJPP N J,DE ROMPH E D.A dynamic traffic forecasting application on the amsterdam beltway[J].International Journal of Forecasting,1977 (13) : 87-103. [5] 张春辉,宋瑞,孙杨.基于卡尔曼滤波的公交站点短时客流预测[J].交通运输系统工程与信息,2011(4):154-159. [6] 郭士永,李文权,白薇,等.基于最小二乘向量机的公交站点短时客流预测[J].武汉理工大学学报(交通科学与工程版),2013(3):603-607. [7] 刘凯,李文权,赵锦焕.短时公交客流小波预测方法研究[J].交通运输工程与信息学报,2010,8 (2):111-117. [8] 李裕奇,赵联文,王泌,等.非参数统计方法[M].成都:西南交通大学出版社,2010. [9] 郑列,宋正义.伪随机数生成算法及比较[J].湖北工业大学学报,2008(5):65-68. (编辑:郝京红) Prediction Algorithm of the Passengers on and off at Tram Stations Based on Statistical Characteristics Jiang Mei1Niu Linbo2 (1. Research Institute of Science and Technology China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031;2. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031) This paper proposes a statistical characteristics-based ridership predicting method to solve the low predication accuracy of the number of passengers on and off as the current prediction method does not consider passenger randomness of urban rail stations. The method covers the following steps: divide and classify historical data according to such factors as dates, time intervals, weather and emergencies; create a distribution model based on the statistical characteristics of the number of passengers on and off; and calculate random numbers in accordance with the statistical characteristics of the predicted passenger flow and the random number generation algorithm. The random number is the predicted number of passengers on and off, which along with the example demonstrates that the distribution model is workable. urban rail; the number of passengers on and off; prediction algorithm; statistical characteristics; random number generation 10.3969/j.issn.1672-6073.2016.04.018 2015-09-14 2015-11-03 姜梅,女,硕士研究生,工程师,从事新型轨道交通规划与线路设计,jiangmei@vip.126.com 四川省科技计划项目(2014GZ0081) U231 A 1672-6073(2016)04-0081-044 算例
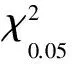
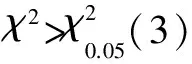
5 结语
