深大宽张裂隙条件下岩质桥基边坡稳定性分析

孙春卫,巫锡勇,凌斯祥,任勇,李涛,廖昕

(西南交通大学 地质工程系,四川 成都 611756)



深大宽张裂隙条件下岩质桥基边坡稳定性分析

孙春卫,巫锡勇,凌斯祥,任勇,李涛,廖昕

(西南交通大学 地质工程系,四川 成都 611756)

某拟建桥位附近地层移动造成桥基岸坡岩体中部分节理面发育成深大宽张裂隙，此类卸荷裂隙往往影响桥基位置的选择，也是桥基荷载下边坡稳定性分析的重点。在现场勘察的基础上，采用赤平投影法分析节理岩体稳定性，确定岩体质量指标，用经验公式结合岩体中宽张裂隙位置确定并修正桥基安全距离。运用离散元和有限元数值模拟深大宽张裂隙及桥基荷载条件下边坡岩体的破坏模式及应力情况，综合分析并验证提出的在安全距离位置桥基荷载条件岸坡的稳定性。研究结果表明，由于裂隙的存在，荷载对裂隙坡前岩体影响不大，但宽张裂隙底部是高应力集中区，将可能导致裂隙再次破坏。在建议的桥位下荷载应力对边坡岩体影响下，桥墩基础是安全的。

宽张裂隙；岩质边坡；稳定性；数值模拟

在岩质边坡工程中，边坡岩体的失稳和破坏模式往往受控于坡体结构面的空间几何关系和结构面的物理力学特性。在桥基荷载条件下的岩质边坡稳定性研究还需要考虑岩体风化卸荷裂隙带的分布。周德培等[1]认为岩质边坡坡体结构除了具有岩性和地质构造特征外，还具有临空面的特性，这使得它直接受到自然营力的作用，而造成坡面一下一定深度的岩体发生很大的变化，如风化、卸荷裂隙等，这种上部岩体风化层常处于上层建筑影响范围内，对工程稳定性影响大。

目前，岩质边坡稳定性分析的方法较多，而不同的方法考虑边坡岩体的工程地质特征的程度和方式各不相同。主要有经验公式法、极限平衡法、有限元法、离散元法等。蒋爵光等[2]应用统计分析、概率方法、定量化理论等数学方法建立了基于边坡岩体质量指标与岩石边坡坡度的岩石边坡稳定性的定量的评价方法。许湘华等[3]在对岩质边坡赤平投影分析的基础上，利用极限平衡分析法对不同破坏模式边坡进行了稳定性计算。詹志峰等[4]采用初步地质评价、经验公式法以及岸坡应力场有限元模拟综合分析清江大桥岩质边坡的稳定性。田洪铭等[5]考虑岩质边坡节理裂隙发育情况，应用ABAQUS有限元软件中的节理材料，采用强度折减法模拟桥基荷载作用下岸坡稳定状态。周涛等[6]基于弹塑性平面离散元原理，分析了岩石边坡的应力场、位移场、塑形屈服区和整体稳定性变化情况。赵志明等[7]在试验确定的岩体结构面强度参数的基础上，采用离散单元法计算分析了岸坡岩体在自然、桥基荷载作用下、地震加桥基荷载作用工况条件下的破坏趋势。然而，在实际岩质边坡工程中，岩体中发育的控制性结构面包括风化卸荷裂隙、深大结构面等是考虑桥基选址和岸坡稳定关键因素。

拟建大桥桥址位于深沟峡谷地区，且周边受煤层采空区影响，地层移动造成桥基岸坡岩体中部分节理面发育成深大宽张裂隙，这类控制性结构面往往影响桥基位置的选择，也是桥基荷载下边坡稳定性分析的重要因素。本文依托拟建桥基所在岩质边坡，考虑岸坡风化卸荷裂隙等结构面发育特征，基于岩体质量指标，运用经验公式法确定边坡稳定坡角和桥基安全距离，然后分别采用有限元和离散元法综合分析岩质边坡破坏模式，得到了桥基荷载对岸坡应力变形的影响规律，对桥基位置的选取和岸坡稳定性评价有重要指导意义。

1 地质概况

拟建桥基位于内蒙古鄂尔多斯境内，线路所处地质构造单元属华北地台内的内蒙地轴、山西断隆及鄂尔多斯台拗三个二级构造单元的结合部位，有轻微的波状褶皱和小断裂构造，除黄河等较大河流的冲洪积平原沉积了厚层第四系覆盖层外，其余地段地层以中生代及古生代沉积岩为主，局部岩层倾角最大可达45°，其余地段岩层平缓或近于水平，多为缓倾的单斜构造，局部呈宽缓波状起伏，地质构造较为简单。研究点附近多为深沟峡谷，分布有二叠系、石炭系等煤系地层。

2 坡体结构特征

拟建桥墩设置在谷深近40～50m的沟谷的岩质边坡上，岩体岩性为砂岩。不考虑区域构造特征时，基础的稳定性决定于岸坡的稳定性和墩台基础下岩体的强度。受区域地质构造和浅表生改造，以及煤层采空区造成地层移动的影响，该桥址边坡岩体节理裂隙发育，现场调查统计得到2组节理，分别为节理面1：315°84°，节理面2：30°70°。另外，层理面产状为215°25°，坡面产状为275°∠80°。

图1 赤平投影分析图Fig.1 Analysis graphic of the stereographic projection

图2 边坡岩体宽张裂隙Fig.2 Wide tension fissure of the slope rock mass

根据该桥基岸坡岩体结构特征，赤平投影分析如图1所示。可以看出，坡面投影穿插滑块12，1，G和3，滑块2的滑动方向指向坡面内部，因此上述滑动方向上的滑块稳定。滑块13和23为两个结构面切割形成的楔形体，有继续滑塌的可能，滑动方向为交线的倾向方向，分别为228°和301°。 J1和J3切割的块体13倾倒破坏是边坡破坏的主要形式。受煤层采空引起地层移动，两组节理均张开，张开宽度最大可达40 cm以上，且延伸很长，坡顶发现走向平行边坡走向的宽张裂隙数条，在岸坡谷底也发现了近期崩塌落石的痕迹,边坡在现阶段处于不稳定阶段，边坡岩体仍有继续崩塌的可能。

总的来说，边坡整体欠稳定，存在坡面岩体崩塌落石的可能性。此外，坡顶存在数条宽张裂隙如图2所示，若桥基置于宽张裂隙之间，桥基的稳定性将决定于裂隙岩体的稳定性，边坡顶部桥基施工加载后，由于垂直荷载引起的侧向力会加剧岸坡岩体的位移，甚至导致坡顶岩体的崩塌，因此，需要对边坡自然状态下及受桥基荷载作用下的边坡稳定性进行评估。

3 边坡稳定坡角的确定

在一般意义上，桥基岸坡的稳定性与自然岸坡的稳定性有关，而自然岸坡的稳定坡角是考虑岸坡自我生存能力下的稳定坡角，在此基础上，可进一步分析加载条件下的岸坡稳定性。利用边坡岩体质量法经验公式来确定岸坡在天然状态下的稳定坡角，利用荷载作用对边坡岩体应力的影响，确定荷载作用下的边坡稳定坡角。

3.1 边坡自然稳定坡角的确定

边坡自然稳定坡度主要采用谢强[8]提出的岩体质量法经验公式计算。通过对岸坡岩体结构面特征的调查和力学性质的试验，三组结构面平均距离分别取120 cm、160 cm和125 cm，回弹值取R=29。按上述经验公式计算得岩体块度为:

133.89≈134(cm)

该地区气候干燥，坡面未见地下水出露，因此取地下水折减系数γw=0.9；高度折减系数取γh=0.9，代入上述公式计算边坡自然稳定坡角为：

θ=0.9×[14.7×ln(0.9×29×lg134)+

13]=64.8≈64°

3.2 荷载作用下边坡稳定坡角的确定

大量的数值分析结果表明，桥基荷载作用下，边坡是否会产生整体破坏主要看荷载对边坡坡面岩体应力的影响。荷载作用产生的附加应力在高陡边坡中有一定的影响范围，基于应力影响范围确定桥基位置基本观点为：如果岩体应力影响范围未到达边坡坡面，则边坡坡面岩体应力不受荷载影响，坡面岩体保持原始稳定状态，边坡不会产生整体破坏，桥基位置是可行的；如果应力影响范围到达坡面，认为荷载对坡面岩体产生了明显的影响，坡面岩体可能不稳定，这种情况的桥基的位置不合理。研究表明，荷载作用的应力影响范围主要与荷载强度、桥基宽度、边坡坡度、边坡岩体质量等有关[9]。桥基安全距离可以用下式表示：

Sf=0.031·α1.482 3·[(1-0.87B)·q]0.7·

(0.5+RMR/200)-0.7

式中：Sf为桥基安全距离，即桥基外缘与坡面的水平距离；α为边坡坡度；q为荷载强度；B为桥基宽度；RMR为岩体质量。

式中相关参数确定如下：

1)边坡坡度

边坡坡度通过野外实测获得，朔州岸桥基及下方边坡平均自然坡度分别为76°、44°。

2)桥基宽度B及荷载强度q

设计桥墩距离坡顶宽张裂隙较近，基础承台初步拟定尺寸为29 m10.5 m，设计设计荷载竖向力43 506 kN，纵向水平力1 151 kN，纵向水平弯矩36 087 kN·m，横向水平力4 669 kN，横向水平弯矩115 922 kN·m。桥基宽度和荷载强度是桥梁荷载的两个因素，由于考虑为平面应变问题，因此不考虑桥基长度，基础宽度B=10.5 m，荷载强度按q=0.4 MPa计算。

3)边坡岩体质量RMR

边坡岩体质量采用宾尼奥斯基的岩土力学分类法，该方法给出的一个总的岩体评分值(RMR)，这个评分值取决于5个通用参数：岩石强度、岩芯质量、地下水条件、节理和断裂的间距及节理的特征[10-11]。采用该方法时将节理和断裂的间距改为岩体的块度[9]。根据野外调查资料及试验资料，则σc=30 Mpa；RQD=55%；岩体块度D=1.34 m；节理表面粗糙，节理张开度大于5 mm，硬岩壁；坡面干燥。根据以上特征得到RMR=52。

4)桥基安全距离确定

将以上参数代入公式可得设计荷载条件下桥基安全距离如下：

Sf=0.031·761.482 3·[(1-0.8710.5)·0.4]0.7·

(0.5+52/200)-0.7=10.2 m

该桥基安全距离没有考虑坡顶裂隙的影响，为基础外缘与坡面边缘的水平距离。由于坡顶存在宽张裂隙，宽张裂隙对桥基的位移及基底岩体应力有较大的影响，对于存在宽张裂隙的岩体高边坡，原则上桥基必须置于裂隙之后。赵文[8]通过对不同桥基水平距离时荷载对坡面岩体应力的影响规律的研究，认为荷载对边坡岩体应力的影响可以用应力影响角来表示，得出边坡上桥基荷载应力影响角约为55°，荷载对坡面岩体应力的影响在应力影响角所对应的位置上最大。如图3所示，荷载应力影响角BAC=55°。假定利用上述方法确定的桥基水平距离为Sf1，如果裂隙深度较小，裂隙与图中的AC线不相交，则认为荷载作用下裂隙对的坡面岩体应力影响不大，桥基水平距离仍为Sf1；当卸荷裂隙与AC线相交时，则将AC平移至AC使其刚好与裂隙相交于F点，得出桥基水平距离Sf2，即图中的BA，当裂隙深度很大时，Sf2值相应变大，此时假定裂隙为新的坡面，裂隙的倾角为新的边坡的坡角，利用前面的方法可以得出假定的这个边坡的桥基水平距离为Sf3，即图中的EA，则此时桥基水平距离取BA与BA中的较小者。

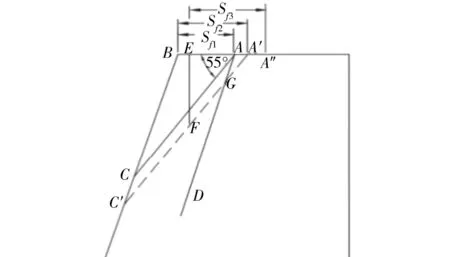
图3 对卸荷裂隙边坡桥基位置的修正示意图Fig.3 Correction of unloading slope bridge foundation position

图4 宽张裂隙影响下的桥基安全距离Fig.4 Bridge safety distance under the influence of the wide tension fissure

边坡顶部靠近边坡发育14#和15#裂隙两条宽张裂隙。一般情况下，桥基宜置于裂隙后，即应置于15#裂隙以后，因此对15#裂隙进行讨论。钻孔揭示该处地表下砂岩厚31.3 m，砂岩下覆泥岩，15#裂隙地表张开宽度约40 cm，该张开裂隙系构造节理受采空区影响而产生地层移动形成的，调查发现该组构造节理延伸长，初步认为张开裂隙的深度较深，贯穿整个砂岩层，即15#裂隙深度30 m以上。当裂隙深度很深时，则桥基安全距离计算时应考虑将裂隙作为虚拟的坡面，虚拟坡面的坡度为90°，则桥基安全距离为：

Sf=0.031·901.482 3·[(1-0.8710.5)·0.4]0.7·

(0.5+52/200)-0.7=13.2 m

桥基安全距离距裂隙为13.2 m，而15#裂隙距坡面13.08 m，则安全桥基距离应距坡面26.28 m以上，如图4所示。按桥基荷载的应力影响角55°计，当裂隙深度大于20.7 m时，就应将裂隙当作虚拟坡面考虑桥基安全距离，实际裂隙深度可达30 m以上，因此，以裂隙当作虚拟坡面考虑。

4 岸坡岩体破坏模式及应力分析

数值分析中各材料计算参数选取如表4所示，根据设计资料，桥墩基底应力按0.4 MPa计，桥基宽度B=10.5 m。

表4 各材料计算参数

4.1 边坡岩体破坏模式分析

离散单元法是求解块体集合体在外力作用下，块体间的相互作用以及运动过程的有效方法，非常适合非连续介质、节理岩体的应力及破坏的分析[12-15]。利用离散单元法，对岸坡的天然状态下、桥基荷载作用下岩体破坏模式及可能产生的破坏范围进行分析。

4.1.1 计算模型及计算参数

基于野外地质调绘结果，建立离散单元模型，考虑到计算的精度要求及模型的合理简化，岩层倾角20°，节理倾角90°，采用二维离散单元软件，建立模型划分块体并在坡面选择了7个观测点如图5所示，令各点的水平位移偏向坡面内的方向为正，反之为负，垂直位移向上为正，反之为负。

图5 离散单元模型及坡面位移记录点Fig.5 Discrete element model and slope displacement record points

4.1.2 天然状态下岩体破坏模式

天然状态下边坡岩体位移趋势特征如图6所示，图中箭头长度表示该点位移的相对大小。从图中可以看出，边坡坡面上及裂隙处岩体位移最大，向坡内部岩体位移越来越小，坡面岩体可能移动块体主要分布在变坡点附近。同时由于裂隙的存在，裂隙前坡体受坡后岩体影响降低，所以天然状态下坡面岩体相对稳定，但是，自然边坡上部陡坡段岩体存在崩塌的可能，自然边坡有变缓的趋势。图7为天然状态下边坡岩体位移速率图示意图，从图中可以看出边坡岩体位移速率最大为墩后方G点处岩体，裂隙靠近墩一侧次之，坡面最小；由此可见边坡岩体由坡后部至坡前位移速率逐渐变小，边坡岩体也逐渐变稳定。

图6 天然状态下岩体位移趋势Fig.6 Trend of the natural state of the rock mass displacement

图7 天然状态下岩体位移速率Fig.7 Displacement rate of rock mass under natural condition

(a)水平位移;(b) 竖向位移图8 天然状态下岩体关键点位移发展趋势Fig.8 Development trend of the key points displacement in the rock mass under natural condition

从图8(a)中可以看出，坡面岩体水平位移随着自然历史的演化逐渐增大，最终趋于稳定。坡面岩体在边坡自然历史发展演化过程中，会产生较大的水平位移，岩体水平位移往往体现在外倾节理的张开、位移直至破坏，边坡上卸荷节理、近期崩塌痕迹证明边坡岩体位移还在发展期。坡面E点裂隙靠墩一侧附近岩体水平位移相对最大，坡中部B点岩体位移次之，D点位移最小。D点处于分割边坡岩体的裂隙顶部，且位于靠近坡面的这部分岩体上，裂隙贯穿整个砂层直至泥岩，降水沿裂隙直达泥岩层形成软弱岩层，另外，裂隙底部也受上坡岩体影响出现顺坡向的应力集中，造成下坡岩体底部向坡外位移大于坡体上部，坡体向坡内向方向倾斜，因而裂隙顶部下坡岩体上的D点出现坡内向方向上的位移。随着边坡岩体的演化，下坡坡体底部位移向坡外继续增大，D点开始向坡外方向移动，最终形成了位移先向坡内方向(正向)，后向坡外方向(负向)的运动状态。

从图8(b)中可以看出，坡面岩体竖向位移同样随着自然历史的演化逐渐增大，最终趋于稳定。坡面岩体竖向位移由坡脚A点至坡后侧岩体位移依次逐渐增加。坡角处竖向位移为坡后侧岩体G点位移的19.1%，其他各点位移均为坡后侧岩体G点位移的50%以上。

根据边坡岩体变形发展历史可知，边坡在形成初期，变形发展迅速，而在边坡形成后期，岩体变形趋于平缓。从图8中也可以看出，在水平位移和竖向位移随时间的变化曲线中，曲线有变形加速阶段和变形平缓阶段。可以认为，天然状态下边坡岩体仍处于变形阶段，目前状态下边坡是处于变形发展平缓期，坡面大部分岩体不会产生较大的变形，坡顶部受节理切割岩体可能产生局部的崩塌落石，裂隙后侧岩体有向坡外位移的趋势。

4.1.3 桥梁荷载作用下岩体破坏模式

桥梁荷载作用下边坡岩体位移趋势特征如图9所示，图中位移向量表示仅由荷载产生的岩体位移，而未包括天然状态下岩体仍将产生的变形。从图中可以看出：荷载作用下，基础底部岩体位移最大，约为天然状态下的51%，沿陡倾节理向下位移，其向下的影响深度约至坡内30 m，向坡外影响至裂隙发育处，由于裂隙的存在，桥梁荷载对裂隙至坡前侧岩体影响不大，向边坡内部岩体位移越来越小，坡面岩体受荷载影响较大的岩体主要分布在基础附近。荷载作用增加了边坡岩体运动的趋势，认为荷载作用对边坡岩体的位移和破坏影响有一定的影响，裂隙的存在未对边坡的总体稳定性产生影响。图10为荷载作用下边坡岩体位移速率示意图，分布规律与天然状态下基本一致，从图中可以看出边坡岩体位移速率主要集中在墩后方G点处岩体，裂隙至坡前侧岩体的位移速率很小，可见荷载对边坡岩体位移速率的影响主要集中在墩后侧，边坡岩体由坡后部至坡前位移速率逐渐变小。

图9 荷载作用下岩体位移趋势Fig.9 Displacement trend of rock mass under loading condition

图10 荷载作用下边坡岩体位移速率Fig.10 Displacement rate of rock mass under loading condition

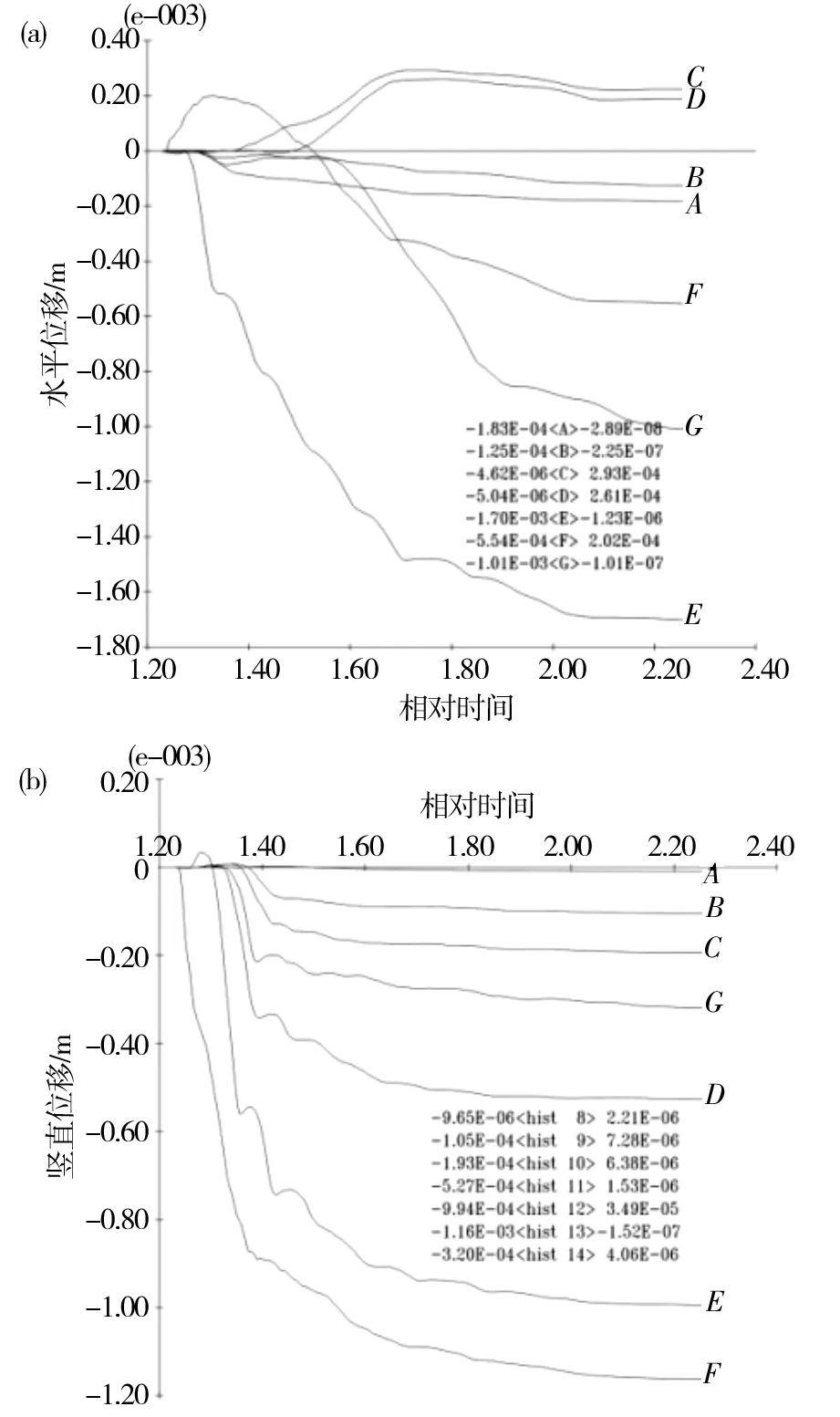
(a)水平位移;(b)竖向位移图11 桥梁荷载作用下边坡关键点岩体位移发展趋势Fig.11 Development trend of the key points displacement in the rock mass under bridge loading condition

桥梁荷载作用下坡面关键点岩体位移特征如图5所示。由图11(a)可以看出，水平位移最大点位于E点；其次是坡后部G点；裂隙前A、B、C及D点位移相对最小，其中C和D点位移方向与其他各点相反，荷载作用下坡顶部分岩体向坡后产生少量位移；裂隙前坡体位移约为E点的7.4%，也说明和桥梁荷载对裂隙前侧岩体的水平位移影响不大。由图11(b)可以看出，桥梁荷载对边坡竖向位移影响最大的是离墩最近的F点和E点，D点次之，A点最小，其中D点竖向位移约为E点的53.0%，说明荷载对裂隙前侧岩体竖向位移的影响要低于后侧的位移，荷载的影响范围是有限的。E点在初始阶段有向上的微小位移，是由于荷载作用下，基础底部岩体向坡下位移相对较大，对其下坡向顶部岩体有向上的应力作用，造成裂隙顶部E点有向上的微小位移，但随着坡体的演化，各测点竖向位移总体趋势是向下的。

4.2 考虑宽张裂隙的边坡岩体应力分析

有限单元法在边坡稳定性分析的应用越来越广泛，它不但能考虑边坡岩体本身的变形对边坡稳定性的影响，而且能给出边坡岩体中应力应变分布，分析边坡破坏的发生和发展过程[16-19]。在考虑14号和15号两条宽张裂隙条件下，对边坡在建议桥位下岩体力学行为特征进行分析。根据现场勘察及钻孔资料，建立边坡数值分析模型如图12所示。

图12 有限元分析模型Fig.12 Finite element analysis model

桥基荷载作用下边坡岩体最大主应力特征如图13所示，由于地层由砂岩、泥岩及煤层组成，地层不均匀，因此岩体应力分布状态也不均匀。受宽张裂隙的影响，在张裂隙底部正下方岩体呈现张应力状态，而在张裂隙底部两侧则呈现较高的压应力状态，即裂隙底部附近区域既有张应力集中现象，也有压应力集中现象。虽有较高的压应力，但压应力远低于岩体抗压强度，因此岩体不会出现因抗压强度不足而破坏的现象，但张裂隙底部的张应力使裂隙有进一步加大加深的趋势。此外，桥基荷载改变了基础底部应力状态，使基底岩体应力显著提高，同样，基底岩体应力远低于岩体抗压强度，基底不会出现岩体抗压强度不足而破坏的现象，基础和基底岩体均是安全的。

图13 边坡岩体最大主应力分布Fig.13 Distribution of maximum principal stress of slope rock mass

桥基荷载作用下边坡岩体最小主应力特征如图14所示，边坡岩体最小主应力分布极不均匀。基础底部附近岩体最小主应力局部存在张应力，但不影响基础及基底岩体的稳定。受宽张裂隙的影响，在张裂隙底部正下方岩体最小主应力呈现张应力状态，且张应力值较高，对岩体的稳定不利。张裂隙底部岩体拉张应力对裂隙附近岩体的稳定不利，对裂隙后方的岩体的稳定影响不大。

图14 边坡岩体最小主应力分布Fig.14 Distribution of the minimum principal stress of slope rock mass

桥基荷载作用下边坡岩体剪应力特征如图15所示，边坡中岩体剪应力集中区主要分布在裂隙底部和基础底部。由于岩体抗剪强度较高，设计荷载下，基础底部产生剪切破坏的可能性不大。但宽张裂隙底部的高剪应力集中则可能导致裂隙的进一步破坏。

图15 边坡岩体剪应力分布特征Fig.15 Shear stress distribution characteristics of rock slope

5 结论

1)采用赤平投影法并结合岩石试验深入探究包括岩石质量和岩体节理面的岩体结构特征，并通过现场地勘资料，计算岩体质量指标，由此通过经验公式分别计算自然条件和桥基荷载条件下岩质边坡稳定坡角，并确定坡面宽大裂隙以修正桥基安全距离是对岩质边坡稳定性分析的较为方便、有效的方法。

2)当不考虑坡顶宽张裂隙的影响时，边坡自然稳定坡角为64°。坡顶宽张裂隙深度较大，对桥墩基础的确定有较大的影响，桥墩基础建议距边坡边缘宜大于26.28 m，距15号裂隙13.2 m。推测桥墩坡内方向存在地下裂隙，将岩体切割成巨块状，但无临空面，岩体无位移空间，因此对边坡和桥基的稳定影响较小。建议在施工开挖后，根据揭示的裂隙规模及发展形态，进行适当处理。

3)边坡岩体卸荷裂隙有逐渐增大的趋势，坡顶岩体存在局部崩塌的可能。桥梁荷载下基础底部岩体位移明显，影响深度约至坡内30 m，向坡外影响至裂隙发育处；由于裂隙的存在，荷载对裂隙至坡前侧岩体及荷载下边坡整体稳定性影响不大。

4)宽张裂隙底部是高应力集中区，将可能进一步导致裂隙的破坏。在建议的桥位下，桥墩基础荷载对边坡岩体应力的影响较小，桥墩基础是安全的，但不排除宽张裂隙前方岩体的进一步破坏，在铁路运营期应该加强对裂隙宽度的监测，以评估对桥基础安全性的影响。

[1] 周德培，钟卫，杨涛. 基于坡体结构的岩质边坡稳定性分析[J]. 岩石力学与工程学报，2008,27(4):687-695. ZHOU Depei, ZHONG Wei, YANG Tao. Stability analysis of rocky slope based on slope structures[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4):687-695.

[2] 蒋爵光，谢强，吴光. 北盘江大桥岸坡稳定性及桥基选址的综合分析[J]. 铁道工程学报，1995,47(3):75-81. JIANG Jueguang, XIE Qiang, WU Guang. Synthetis analyses on stability of river’s bank slopes and disposition of bridge foundations for beipanjiang railway bridge[J]. Journal of Railway Engineering Society, 1995, 47(3):75-81.

[3] 许湘华, 朱能文, 方理刚, 等. 贵州地区浅变质岩公路边坡稳定性分析[J]. 铁道科学与工程学报，2010, 7(4): 42-48. XU Xianghua, ZHU Nengwen, FANG Ligang, et al. Stability analysis of shallow metamorphic rock slope in guizhou area[J].Journal of Railway Science and Engineering, 2010, 7(4):42-48.

[4] 詹志峰，谢强，赵文. 峡谷区岩质桥基岸坡稳定性分析方法研究[J]. 四川大学学报(工程科学版), 2003, 35(6): 31-35. ZHAN Zhifeng, XIE Qiang, ZHAO Wen. Analysis method research on rocky slope stability of bridge foundation in gorge area[J]. Journal of Sichuan University(Engineering Science Edition), 2003, 35(6): 31-35.

[5] 田洪铭, 陈卫忠, 郑鹏强, 等. 桥梁荷载下跨谷拱桥岩质桥基岸坡稳定性分析[J]. 岩土力学，2013，34(增1)：379-385. TIAN Hongming, CHEN Weizhong, ZHENG Pengqiang, et al. Stablity analysis of rocky slope for arch bridge foundation in gorge area[J]. Rock and Soil Mechanics, 2013，34(Suppl1):379-385.

[6] 周涛，张家生，陈晓斌. 龙滩电站航道岩石边坡弹塑性平面离散元分析[J]. 铁道科学与工程学报, 2006, 3(4):62-67. ZHOU Tao, ZHANG Jiasheng, CHEN Xiaobin. Two dimensional elastoplastic distinct element analysis of rock slope in navigation route of longtan hydropower station[J]. Journal of Railway Science and Engineering, 2006, 3(4):62-67.

[7] 赵志明，吴光，王喜华，等. 金沙江特大桥左岸岸坡岩体结构面强度参数取值及工程稳定性评价[J]. 工程地质学报，2012, 20(5)：768-773. ZHAO Zhiming, WU Guang, WANG Xihua, et al. Strength of structure surfaces and slope stability evaluation for left rock slope of Jinshajiang bridge[J]. Journal of Engineering Geology, 2012, 20(5): 768-773.

[8] 谢强. 道路岩石边坡坡度确定方法的研究[J]. 中国公路学报，2000，13(2)：24-26. XIE Qiang. Research on calculating method of rock slope angle for highway and railway[J]. China Journal of Highway and Transport,2000, 13(2):24-26.

[9] 赵文. 荷载作用下高陡边坡岩体力学行为及桥基位置确定方法研究[D]. 成都：西南交通大学，2001. ZHAO Wen. Study on mechanical behaviour of rock mass on high-steep slope under load and determination of bridge foundation position[D]. Chengdu: Southwest Jiaotong University, 2001.

[10] Bienlawski Z T. Engineering rock mass classification[M]. New York Intercience Publication, Viley, 1993.

[11] Bienlawski Z T. The geomechanics classification in rock engineering applications[J]. Isrm Motntrewx Proc.int.cong.on Rock Mech.1979(1):55-95.

[12] 刘凯欣, 高凌天. 离散元法研究的评述[J]. 力学发展, 2003, 33(4): 483-485. LIU Kaixin, GAO Lingtian. The comments of discrete element method[J]. Advances in Mechanics, 2003, 33(4): 483-485.

[13] 胡夏嵩，赵法锁. 低应力区地下洞室开挖后围岩位移二维离散元数值模拟[J]. 水利水电技术，2004，35(9)：37-39. HU Xiasong, ZHAO Fasuo. 2D discrete element method simulating displacement characteristics of surrounding rock mass of underground excavation in the low ground stress region[J].Water Resources and Hydropower Engineering, 2004, 35(9): 37-39.

[14] 曹帅，杜翠风，母昌平，等. 崩落法转充填法采矿地表移动二维离散元程序数值模拟及其规律验证[J]. 岩土力学，2015，36(6)：1737-1751. CAO Shuai, DU Cuifeng, MU Changping, et al.UDEC-based modelling of mining surface movement due to transforming from block caving to sublevel filling and its law verification[J]. Rock and Soil Mechanics, 2015, 35(6): 1737-1751.

[15] 雷远见, 王水林. 基于离散元的强度折减法分析岩质边坡稳定性[J]. 岩土力学, 2006, 27(10): 1693-1698. LEI Yuanjian, WANG Shuilin. Stability analysis of jointed rock slope by strength reduction method based on UDEC[J]. Rock and Soil Mechanics, 2006, 27(10): 1693 -1698.

[16] 陈祖煜. 土质边坡稳定分析：原理·方法·程序[M]. 北京：中国水利水电出版社，2003. CHEN Zuyu. Soil slope stability analysis：theory，methods and programs[M]. Beijing：China Water Power Press，2003.

[17] 朱伯芳. 有限单元法原理与应用[M]. 北京：中国水利水电出版社， 1998. ZHU Bofang. Principle and application of FEM[M]. Beijing： China Water Power Press，1998.

[18] 赵尚毅，郑颖人，邓卫东. 用有限元强度折减法进行节理岩质边 坡稳定性分析[J]. 岩石力学与工程学报，2003，22(2)：254-260. ZHAO Shangyi, ZHENG yingren, DENG Weidong. Stability analysis of jointed rock slope by strength reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 254-260.

[19] 张季如. 边坡开挖的有限元模拟和稳定性评价[J]. 岩石力学与工程学报，2002，21(6)：843-847. ZHANG Jiru. Finite element simulation and stability analysis of slope excavation[J]. Chinese Journal of Rock Mechanics and Engineering，2002，21(6)：843-847.

Analysis of rock slope stability of bridge foundation under the condition of wide tension fissure

SUN Chunwei, WU Xiyong, LING Sixiang, REN Yong, LI Tao, LIAO Xin

(Department of Geological Engineering, Southwest Jiaotong University, Chengdu 611756, China)

Some joint surfaces develop into the deep and wide tension fissure in the rock slope of a bridge foundation because of stratigraphic heave. The fissure, one type of stress-release crack contributing to human activity, has a great influence on the determination of the position of bridge foundation and is the focal point to the analysis of rock slope under bridge loading. On the basis of field investigation, the method of stereographic projection was utilized to analyze the stability of the jointed rock mass, and the safe distance of bridge foundation was obtained by calculating the empirical formula involving RMR and fixing that after defining the position of the wide fissures. The failure model and stress regime of the rock mass were analyzed using finite element method and Discrete element method. The rock slope stability of the bridge foundation under the proposed safe distance position was analyzed comprehensively and verified. The analysis results indicate that the front of the rock mass slope is not susceptible to the load for the existence of the wide tension fissures, while the bottom of the fissure is high stress concentration area where it is prone to failure of the rock mass again. The bridge foundation is safe under the proposed position.Key words：wide tension fissure; rock slope; stability; numerical simulation

2016-01-11

国家自然科学基金资助项目(41172261)

巫锡勇(1963-)，男，四川成都人，教授，从事岩石风化及其工程特性评价、岩土体稳定性研究;E-mail:wuxiyong@163.com

U212.22

A

1672-7029(2016)11-2154-09