水平掏土迫降纠倾法机理分析及计算方法
2016-12-16邓正定张小兵
邓正定,张小兵,王 珑
(1.中国铁道科学研究院, 北京 100081; 2.中铁西北科学研究院有限公司, 甘肃 兰州 730000)
水平掏土迫降纠倾法机理分析及计算方法
邓正定1,张小兵2,王 珑2
(1.中国铁道科学研究院, 北京 100081; 2.中铁西北科学研究院有限公司, 甘肃 兰州 730000)
针对水平掏土成孔形成的土条带侧向应力解除,条带边缘会产生剪胀滑移破坏的特征,基于对其破坏模式分析的基础上,运用经典土力学观点,假定土体弹性区与塑性区交界处服从摩尔-库伦准则,认为塑性区土体产生滑移剪切破坏,弹性区土体主要承担上部荷载,服从虎克定律,提出针对水平掏土成孔土压缩变形的计算方法,并应用于建筑物纠偏实例中,对计算结果和工程应用结果比较表明,该方法能够很好计算出掏土临界应力以及掏土孔孔径、土条宽度等相关重要参数,预测附加沉降量,并与实际结果吻合较好,证明了计算方法的正确性和合理性,填补了纠偏设计不能预测沉降量的理论空白,对于建筑物纠偏设计与施工具有较强的指导意义。
纠偏; 掏土成孔; 机理分析; 计算方法
随着国民经济的快速发展和基础设施建设工程增加,各式各样的建筑形式不断涌现,建筑规模也越来越大,一些建筑物不得不座落在地质条件差的场地上,由于上部结构的多样性,地基基础的复杂性及不确定性,再加上勘察、设计、施工等多方面的原因,近年来建筑物倾斜事故时有发生[1]。目前,建筑物纠倾的方法共有三十多种,根据处理方式可归结为迫降法、抬升法、预留法、横向加载法和综合法(或组合纠倾法)等五大类[2], 由于大部分建筑倾斜是由于地基土的不均匀沉降引起,故在各种纠倾方法中,水平掏土迫降纠倾法适用范围广,纠倾沉降量容易控制,适用于软土地基、黄土地基、片筏基础上的倾斜建筑物。通过大量工程实践,获得了许多关于掏土纠倾法的有价值结论[3],但由于建筑物掏土纠倾的特殊性,此方法还大多以不完全适合的土力学理论为导向,借鉴以往设计经验,来指导工程实践,至今尚无成套的、系统的理论体系,对该方法的应用和推广造成较大阻碍。目前针对水平掏土纠倾的理论研究还存在以下问题:
(1)针对纠倾过程中孔间土的破坏模式、损伤机理尚无系统研究,尚无合理的计算掏土成孔后地基土附加沉降的计算方法,从而无法精确计算掏土量及附加沉降;
(2)由于掏土孔的存在,相当于孔间土侧限解除,土体产生部分滑移剪切破坏,这与传统的地基土附加沉降计算方法有较大区别。
针对以上主要问题,通过理论研究、结合具体工程实例等方法,运用经典土力学方法,提出能够适用于水平掏土纠倾法的附加沉降计算方法,并应用于实际纠倾工程中进行验证,为今后采用此法的纠倾加固工程提供理论依据,具有广阔应用前景和学术价值。
1 水平掏土纠倾法原理及土的破坏模式
1.1 水平掏土纠倾法原理
水平掏土迫降纠倾法是指在倾斜建(构)筑物沉降较少的一侧基础底部,采用人工或机械按照设计的次序和掏土量进行水平掏土,以消减基底的承压面积,增大其附加应力,随着基底附加应力的增大,基底土体由压密变形向塑性变形发展,同时辅以锚索加压进一步增加基地应力,使土体再次被压缩而引起建(构)筑物下沉,如图1。

图1 水平掏土迫降纠倾法示意
1.2 孔间土的破坏模式
建筑物的荷载通过基础传递到土中,因此基础底面的压力分布形式将对土产生直接影响,其涉及到上部结构物、基础和地基土共同作用问题,是一个十分复杂的课题,因此在简化分析时仅看作压力接触问题,即看作上部结构自重直接传递到土体中,由于掏土孔的存在,会导致承担荷载面积减小,而上部荷载大小不变,从而造成土体应力增加,引起应力重分布,同时由于孔间土侧限应力减少,造成孔边缘形成塑性破坏区,随着掏土量增加,塑性区范围增大,部分土体受剪胀破坏,见图2。基于以上实际,可将孔间土看成原状土及破坏土,孔间土在初始状态时全部为原状土,随着应力增加,侧向应力解除,孔间土边缘部分土体逐渐受剪胀破坏,滑入孔中,在掏土造就应力增加的过程中,其受力特性是两种土体动态变化的综合反映。

图2 孔间土破坏模式
对于掏土纠倾过程中的土体,在压应力和剪应力作用下,当达到临界状态时,部分土体开始发生剪胀破坏,由于土体前期已经过固结,可认为原状土不再发生体应变,将受剪胀破坏土体所占比例用ω表示,则孔间土的力学特性可表示为二者加权平均值:
S=(1-ω)Si+ωSd
(1)
式中:S为土的某种力学指标;Si与Sd分别为原状土和破坏土的同一力学指标。
2 水平掏土成孔机理
2.1 掏土成孔塑性力学分析
由于掏土成孔后,在上部荷载P一定时,随着受荷面积A不断减小,孔间土应力σ不断增加,有如下关系:
(2)
(3)
式中:σ0为掏土前初始应力;P为上部荷载;A0为掏土前基底面积;σ为掏土成孔后条带土竖向应力;D为掏土孔直径;L为掏土孔间土宽度。
由于掏土孔的存在,孔周地基土初始应力被解除,随着应力的增加,孔周一定范围地基土将由弹性状态转为塑性状态,且塑性区范围随着掏土量的增加而增加,而在塑性区之外的土体仍保持弹性状态,由于孔间土破坏往往发生在孔间土宽度最小处,故可将孔间土看成近似宽度一致的条带,孔间土水平方向应力由边缘向中间逐渐增大,孔间土受压缩剪胀破坏,其受力特性如图3所示。

图3 孔间土单元体受力分析
考虑单元力系的平衡方程有:
(4)
式中:r为土条中某一点处到掏土孔中心的水平距离;σr为某一点处径向应力;σe为某一点处环向应力。
假设孔间土中,塑性区土体服从摩尔-库伦准则,则有如下关系:
σe(1-sinφ)-σr(1+sinφ)=2ccosφ
(5)
式中:c为土体粘聚力;φ为土体内摩擦角。
结合公式(4)、(5)得到:
(6)
通过对式(6)非齐次微分方程求通解可得:
(7)
式中:C为待定常数。
(8)
由于在掏土迫降时,只需考虑掏土孔两侧土的应力状态,而忽略掏土孔上下方的应力,在两侧土体塑性区与弹性区交界处,可认为环向应力与由上部荷载引起的竖向应力近似相等,应力只与掏土孔削弱面积相关,结合式(3)可得:
(9)
同时σe、σr需满足:
(10)
结合式(8)、(9)、(10)联解得掏土孔中心在水平方向的塑性区范围为:
(11)
由上式可知,塑性区范围大小随上部荷载、掏土孔削弱面积以及掏土孔径的增大而增大。当2r≤D时,孔间土没有形成塑性区,即孔间土为全弹性区;当孔间土宽度L≥2r-D时,孔间土部分形成塑性区,部分为弹性区,即孔间土为半塑性半弹性区,当孔间土宽度L<2r-D时,塑性区范围覆盖整个孔间土宽度,即形成全塑性区。
由式(11)可知,当r=D/2时,孔间土全部为弹性区,但即将形成部分塑性区,即处于临界状态,这在纠偏中是很重要的参数,即可采取“掏土至临界,锚索加压至破坏”的措施,设计掏土量为达到临界应力即可,再通过锚索加压使塑性区范围扩大,加速沉降量,计算得掏土临界应力值为:
(12)
式中:σcr为即将形成塑性区时临界应力值。
结合式(3)、(12)可得达到临界应力时,所对应的掏土孔间土条宽度与各相关参数的关系为:
(13)
式中:Lcr为达到临塑状态时孔间土条宽度。
同样,由式(11)可知,当r=(D+L)/2时,条带土全部为塑性区,即无弹性区,计算可得条带土形成全塑性区时临界应力值σqr为:
(14)
2.2 地基土附加沉降计算方法
假定土体的剪胀破坏是瞬时发生,无时间效应。对于孔间土来说,塑性区土体大部分受到剪切滑移破坏,可将这部分土体当成损伤土,为描述孔间土损伤区的发展,需建立描述损伤发展的方程,即损伤演化方程。沈珠江[4~6]等结合大量实验研究认为,损伤伴随着应变的发展而发展,但结合掏土成孔的特点,将塑性理论与损伤理论相联系,可认为损伤区伴随着塑性区的范围发展而发展,其损伤演化方程可表示为:
(15)
式中:a为损伤修正系数,可取0.8~0.9。
沈珠江等[4]认为原状土变形性状近似为弹性体,即服从虎克定律,则非损伤区原状土应力应变关系有:
(16)
式中:εe为非损伤区应变;E为原状土弹性模量。
孔间土由于部分土体发生剪切破坏,由于损伤土会滑移到掏土孔中,可承担的荷载较小,为简化计算,可忽略损伤土的应力,认为荷载全部由弹性区原状土承担,则有:
ε=εe
(17)
式中:ε为孔间土总应变。
由于土溃变导致实际承担荷载孔间土面积A进一步减少,故可认为非损伤区土的压缩变形是一个新的平衡过程,则原状土区土体承担的应力为:
(18)
由于掏土造就应力小于临界应力时,孔间土同样可认为弹性变形,同样服从虎克定律,则可建立最终能够描述掏土成孔后地基土附加沉降的计算方程:
(19)
从式(19)可知,掏土造就应力超过临界应力时,由于可承担荷载面积随着破坏区的增大进一步减小,应力进一步增大,沉降速率会明显加快,进入“恶性”循环,这就是在纠偏实践中,当掏土至临界后,辅以少量锚索加压或堆载,都能起到事半功倍效果的原因。
3 计算方法在建筑纠偏中的应用
3.1 工程概况
甘肃省某高层商住楼为地下1层,主楼地上17层,裙楼3层,主楼总高度为50 m。其中主楼为剪力墙结构,裙楼均为框架剪力墙结构;基础形式均为平板式筏形基础,且主楼与裙楼筏板相连。筏板东西向最大长度43 m,南北向宽度36 m。筏板埋深5.2 m,筏板板厚1.0 m,筏板外伸1.2 m,筏板下为厚150 mm的C20素混凝土垫层,垫层与筏板之间做建筑防水,防水层上做50 mm厚C20混凝土保护层,垫层下做厚500 mm的3∶7灰土垫层。
该楼所在场地属于关川河西岸二级阶地后缘。根据详勘报告及后期勘察资料显示,场地地层自上而下主要由黄土、角砾及泥岩三层组成,由于对湿陷性黄土进行了孔内深层强夯法(DDC法)整片处理,该楼基础坐落于黄土复合地基土地层之上,复合地基土物理力学指标见表1,倾斜变形情况见图4。

表1 复合地基土物理力学参数
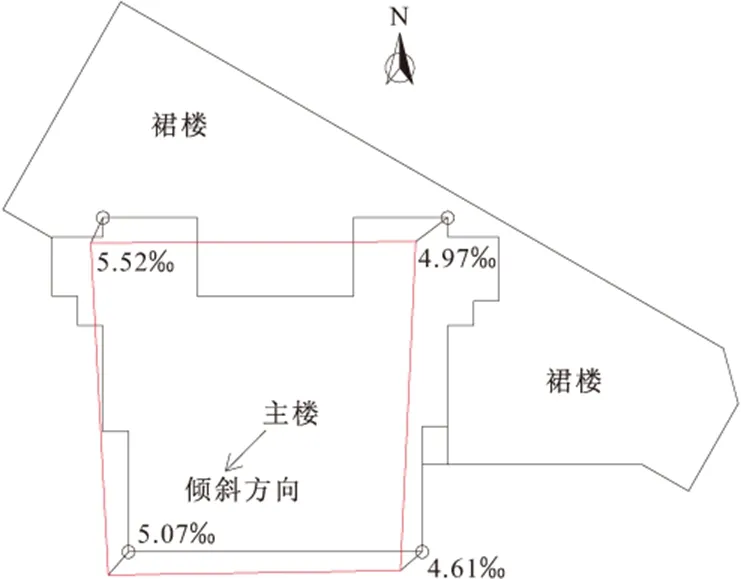
图4 大楼平面示意
3.2 相关参数计算
由于大楼存在设计缺陷,导致偏心严重,建筑物基础底面的压应力可按下式计算[7~9]:
(19)
式中:pk为荷载效应标准组合时,基础底面平均压应力;pkmax为荷载效应标准组合时,基础底面边缘最大压应力;pkmin为荷载效应标准组合时,基础底面边缘最小压应力;Fk+Gk为上部荷载组合;A为基础底面面积(m2);Mp为偏心荷载;W为基础底面抵抗矩(m3)。
通过计算可得掏土前各区域地基应力分布等势图如图5所示。
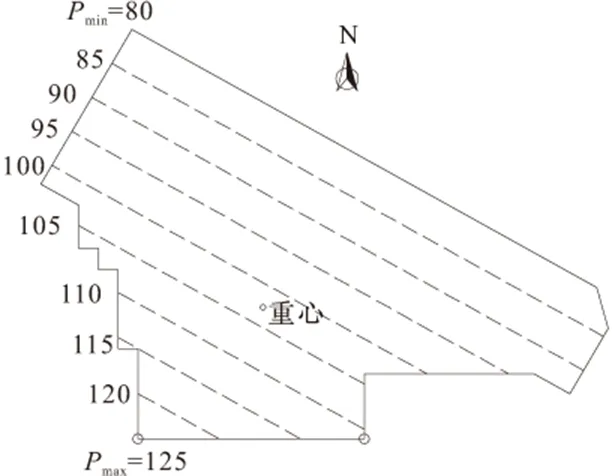
图5 掏土前各区域地基应力等势图/kPa
结合钻孔机械特点,一般可供选择钻孔孔径为130 mm或150 mm,由于大楼东北侧筏板边缘目标沉降量为70~80 mm,目标沉降量较大,而孔周土破坏压缩后需占用部分体积,故选择钻机孔径为150 mm较为合适。
结合式(13)及各相关物理参数进行计算,各区域达到临界状态时所需最小土条宽度Lcr如图6所示。
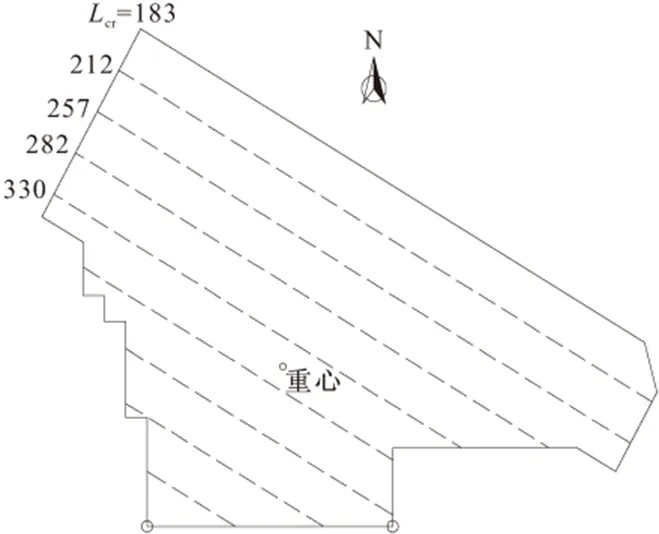
图6 各区域达到临界状态时所需最小土条宽度/mm
结合式(14)及各相关物理参数进行计算,各区域达到全塑性区状态时所需最小土条宽度Lqr如图7所示。
本着“掏土至临界,锚索加压至破坏”的原则,并使东北侧塑性区范围适当扩大,甚至达到全塑性区,西南侧介于全弹性区与全塑性区之间,掏土区范围为重心以东南1~2 m,根据纠倾目标,东北边缘所需沉降量为70~80 mm,重心附近所需沉降量为40~50 mm,故设计东北侧边缘掏土孔土条宽度为40 mm,结合式(18)计算可得孔间土压缩变形量为65 mm,设计重心以东南边缘掏土孔土条宽度为60 mm,计算可得孔间土压缩变形量为28 mm,基本与大楼纠倾目标值相吻合。
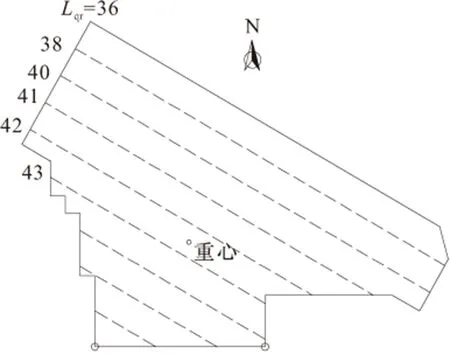
图7 各区域达到全塑性状态时所需最小土条宽度/mm
3.3 纠倾效果验证
2014年11月1日开始对大楼进行纠倾,历时4个多月,大楼最大倾斜率由原来5.52‰回到2.54‰,达到我国规范的建筑物安全使用要求,监测点布置及沉降曲线分别见图8、9。
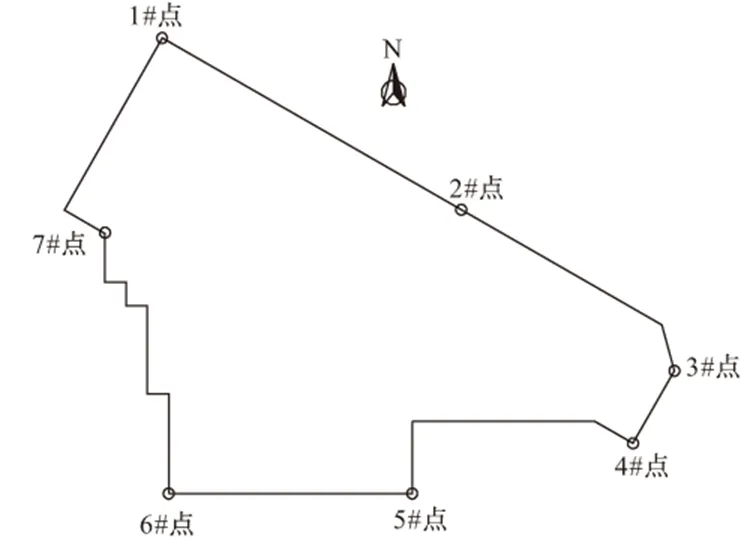
图8 各沉降观测点布置

图9 各观测点沉降曲线
由图9可知,大楼沉降基本趋于稳定,位于东北侧的1、2、3#观测点沉降值为60~70 mm之间,西南角的6#点沉降最小,约10 mm,为加固侧竖井开挖及拖带沉降影响所致,大楼附加沉降量与计算结果基本一致,说明本文所提出的计算方法有较好的实用性。
4 结论与建议
本文通过经典土力学与现代损伤力学结合,构建出简单实用的针对掏土迫降纠偏附加沉降的计算方法,并成功应用于纠偏工程实例,得出以下结论:
(1)基于摩尔-库伦准则,分析孔间土的应力分布特点,得出孔间土塑性区范围,以及达到临界状态时所对应的土条宽度,为纠倾设计提供依据;
(2)引入损伤力学观点,根据设计参数预测出最终附加沉降量,填补了以往纠偏只能依靠经验,不能准确计算的空白;
(3)将所提出的计算方法应用于基础形式复杂的纠偏工程中,计算结果与实际沉降量基本吻合;
(4)本文提出的计算方法需确定的材料参数较少,且都是土力学最基本的物理参数,简单而实用。
(5)本文所提出计算方法,没有考虑损伤区所承担荷载,而实际上,损伤区也承担一定荷载,服从特定的屈服准则,后续应加强研究,以建立更加符合掏土纠偏实际的计算方法。
[1] 唐业清, 万墨林. 建筑物改造与病害治理[M]. 北京: 中国建筑工业出版社, 2000.
[2] 王 桢. 锚索技术用于建筑物可控精确纠倾[J]. 施工技术, 2011, 40(s1), 24-27.
[3] 赵锡宏, 孙 红, 罗冠威. 损伤土力学[M]. 上海: 同济大学出版社, 2000.
[4] 沈珠江. 结构性粘土的弹塑性损伤模型[J]. 岩土工程学报, 1993, 15(3), 21-28.
[5] 沈珠江. 结构性粘土的非线性损伤力学模型[J]. 水利水运科学研究, 1993, (3), 247-255.
[6] 何开胜, 沈珠江. 结构性粘土的弹粘塑损伤模型[J]. 水利水运工程学报, 2002, (4), 7-13.
[7] 唐业清, 徐国彬. 特种工程新技术(2009) [M]. 北京:中国建筑工业出版社, 2009.
[8] CECS 225:2007, 建筑物移位纠倾增层改造技术规范[S].
[9] JGJ 270-2012, 建筑物倾斜纠偏技术规程[S].
Mechanism Analysis and Calculation Methed of Horizontal Soil Landing Rectifying Method
DENGZheng-ding1,ZHANGXiao-bing2,WANGLong2
(1.China Academy of Railway Sciences, Beijing 100081, China; 2.Northwest Research Institute Co Ltd of CREC, Lanzhou 730000, China)
Because of the characteristics of the horizontal soil into hole forming soil lateral stress relief, edge banding producing dilatancy sliding failure, and based on the failure mode analysis, on the basis of using the classical soil mechanics point of view, it assumes that the elastic zone and the plastic zone of soil on the border obey Moore-coulomb criterion, shear damage responses of the plastic zone of soil slip, the elastic zone soil mainly undertakes the upper load, obey hooke’s law, proposed in view of the level of soil pore forming and the calculation method of soil compression deformation and applied to the building rectifying example. The comparing result of the calculation results and engineering application showed that this method can calculate the soil stress and critical soil hole diameter, width related important parameters, such as soil, additional subsidence prediction, and are in good agreement with the actual results, proving the correctness and rationality of the calculation method and fill in the gap theory, in which design cannot predict settlement, and has strong guiding significance in rectifying for building design and construction.
rectifying; soil pore forming; mechanism analysis; calculation method
2015-12-03
2016-03-03
邓正定(1987-),男,江西萍乡人,博士研究生,研究方向为建筑物纠倾加固(Email:dengzhengding@126.com)
中铁科学研究院有限公司科技开发项目(2015-SQ1-05)
TU746.3
A
2095-0985(2016)05-0038-06
