乙二醇-1,4-丁二醇-二乙二醇三元物系气液平衡研究
2016-12-16陈卫航李怡恩张婕蒋元力王训遒
陈卫航,李怡恩,张婕,蒋元力,王训遒
(1.郑州大学 化工与能源学院,河南 郑州 450001;2.河南能源化工集团,河南 郑州 450046)
乙二醇-1,4-丁二醇-二乙二醇三元物系气液平衡研究
陈卫航1,李怡恩1,张婕1,蒋元力2,王训遒1
(1.郑州大学 化工与能源学院,河南 郑州 450001;2.河南能源化工集团,河南 郑州 450046)
实验主要测定了6.67 kPa下乙二醇-1,4-丁二醇-二乙二醇的三元体系气液相平衡数据.使用广泛适用的WILSON、NRTL和UNIQUAC模型对实验数据进行拟合关联,结果表明:实验数据与预测数据之间最大平均相对误差为5.326%,可以满足工程上分离设计的要求.
煤制乙二醇;三元气液平衡;NRTL方程;Wilson方程;UNIQUAC方程
0 引言
作为一种重要的有机化工原料,乙二醇广泛应用于生产聚酯纤维、防冻剂和非离子表面活性剂等,其中90%用于聚酯行业[1].近些年得益于聚酯行业的飞速发展,乙二醇消费也日趋增长,而我国乙二醇的产能严重不足,严重依赖进口,这必将严重影响相关行业的正常发展.目前,世界上生产乙二醇的方法主要有石油路线[2]和非石油路线[1,3-4]两种.但我国由于石油资源贫乏而煤炭资源相对丰富,因此发展煤制乙二醇技术符合我国发展需求.然而煤制乙二醇路线中会产生较多的副产物如:1,4-丁二醇、二乙二醇和1,6-己二醇等,其中二乙二醇含量较高且具有较好的经济价值,需要将其分离提纯.乙二醇及其副产物的沸点较高,实际工业生产中采用减压精馏的方法进行分离.笔者对乙二醇-1,4-丁二醇-二乙二醇物系在6.67 kPa下进行气液相平衡数据的实验测定,并利用相关模型进行模拟,为该物系分离工艺的设计提供基础数据.
1 实验部分
1.1 实验试剂
乙二醇:分析纯,质量分数≥99.5%,天津市风船化学试剂科技有限公司.1,4-丁二醇:分析纯,质量分数≥99.5%,上海晶纯生化科技股份有限公司.二乙二醇:分析纯,质量分数≥99.5%,天津市化学试剂二厂.
1.2 实验装置及操作
实验选用操作简单、稳定性好的气相冷凝循环平衡釜(见下图1),该装置已经过相关物系验证[5-7];真空泵;U型管水银压差计;0~50 ℃和100~150 ℃温度计各1支,使用过程中均已进行零点校正、刻度校正及露颈校正.实验中,选取低沸点的乙二醇为主体,向其中加入配置好的1,4-丁二醇与二乙二醇溶液,连接好装置后打开加热套开关与真空泵开关,保持体系内部压力始终维持在6.67 kPa,当温度稳定后即可认为体系达到平衡状态,继续加热1.5 h使体系处于完全平衡
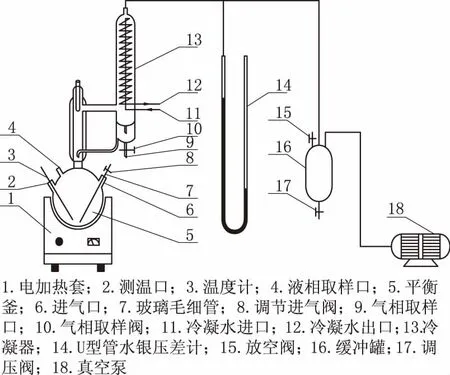
图1 实验装置
状态,记录平衡时的温度值,取样0.5 mL进行检测.然后再向平衡釜中加入一定量1,4-丁二醇与二乙二醇,重复上述操作,得到一系列浓度的气液两相样品.
1.3 分析方法
将得到的气液样品进行色谱检测,并采用归一化法进行定量分析.所用气相色谱为上海科创色谱仪器有限公司GC-9800气相色谱仪,分析条件如下:50 m×0.32 mm×0.25 μm的聚乙二醇毛细管柱;FID检测器;高纯氮载气;柱前压0.045 MPa;尾吹压力0.035 MPa;氢气压力0.03 MPa;空气压力0.05 MPa;分流流量60 mL/min;柱箱温度180 ℃;气化室温度300 ℃;检测器温度280 ℃;进样量0.1 μL.
2 实验结果
实验测定了6.67 kPa下乙二醇(1)-1,4-丁二醇(2)-二乙二醇(3)三元物系气液相平衡数据,实验结果见表1.

表1 6.67 kPa下乙二醇(1)-1,4-丁二醇(2)-二乙二醇(3)三元体系气液平衡数据
注:气液数据均为质量分数.
3 三元体系数据关联
采用Aspen软件,选用WILSON[8-9]模型、NRTL[10]模型和UNIQUAC[11-12]模型,分别对实验数据进行关联,以检测实验数据与检测结果之间的吻合度.
多元体系WILSON方程模型参数表达式如下:
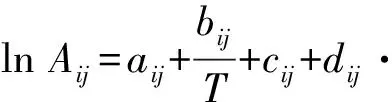
(1)
多元体系NRTL方程模型参数表达式如下:
Gij=exp(-aij·tij);
(2)
(3)
Aij=cij+dij·(T-273.15).
(4)
多元体系UNIQUAC方程模型参数表达式如下:
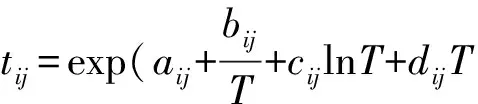
(5)
式中:aij、bij、cij、dij、eij及fij分别为各模型二元交互作用参数.
采用阻尼最小二乘法对所选物系的气液平衡数据进行关联,选用目标函数:
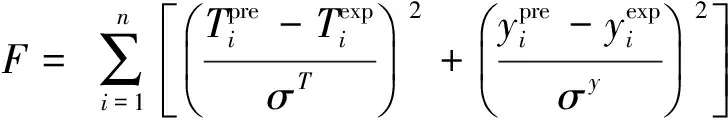
(6)
其中,σT和σy是温度和气相组成的标准偏差,代入数据回归得到二元交互作用参数.笔者所在课题组已经测得该体系中各二元物系的汽液平衡数据,经热力学一致性检验,所得数据均符合热力学一致性[5].二元交互作用参数如表2~4所示.
分别采用二元交互作用参数代入Aspen Plus对所测得的液相数据进行模拟得到规定条件下的气相预测数据如表5所示.由模拟所得数据与实验数据进行比较得到其相对误差见表6.
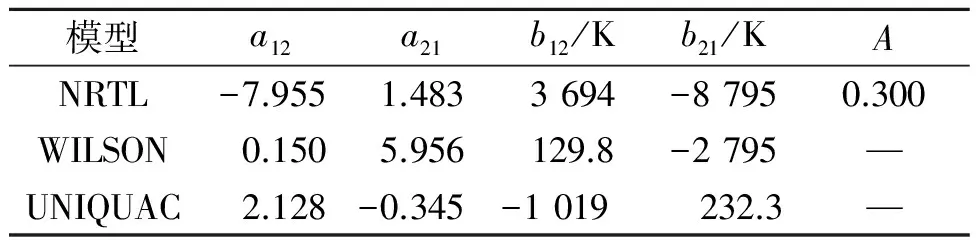
表2 6.67 kPa下乙二醇(1)-1,4-丁二醇(2) NRTL、WILSON和UNIQUAC模型二元交互作用参数
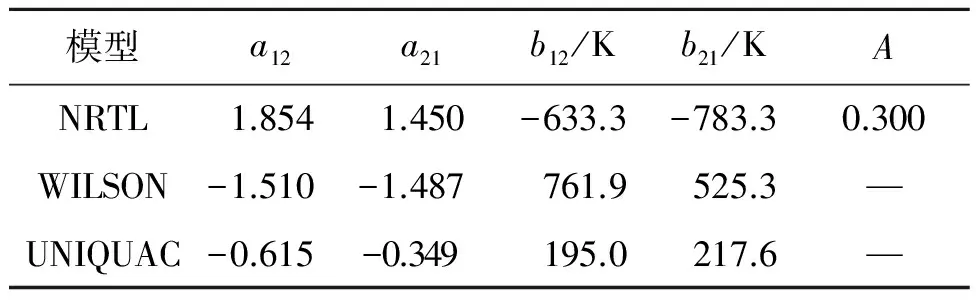
表3 6.67 kPa下1,4-丁二醇(2)-二乙二醇(3) NRTL、WILSON和UNIQUAC模型二元交互作用参数
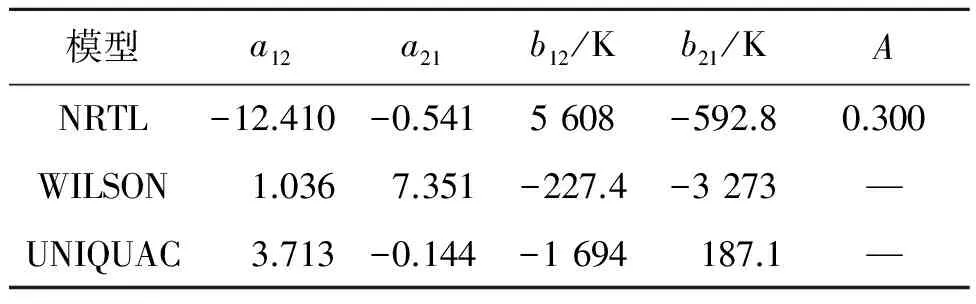
表4 6.67 kPa下乙二醇(1)-二乙二醇(3) NRTL、WILSON和UNIQUAC模型二元交互作用参数
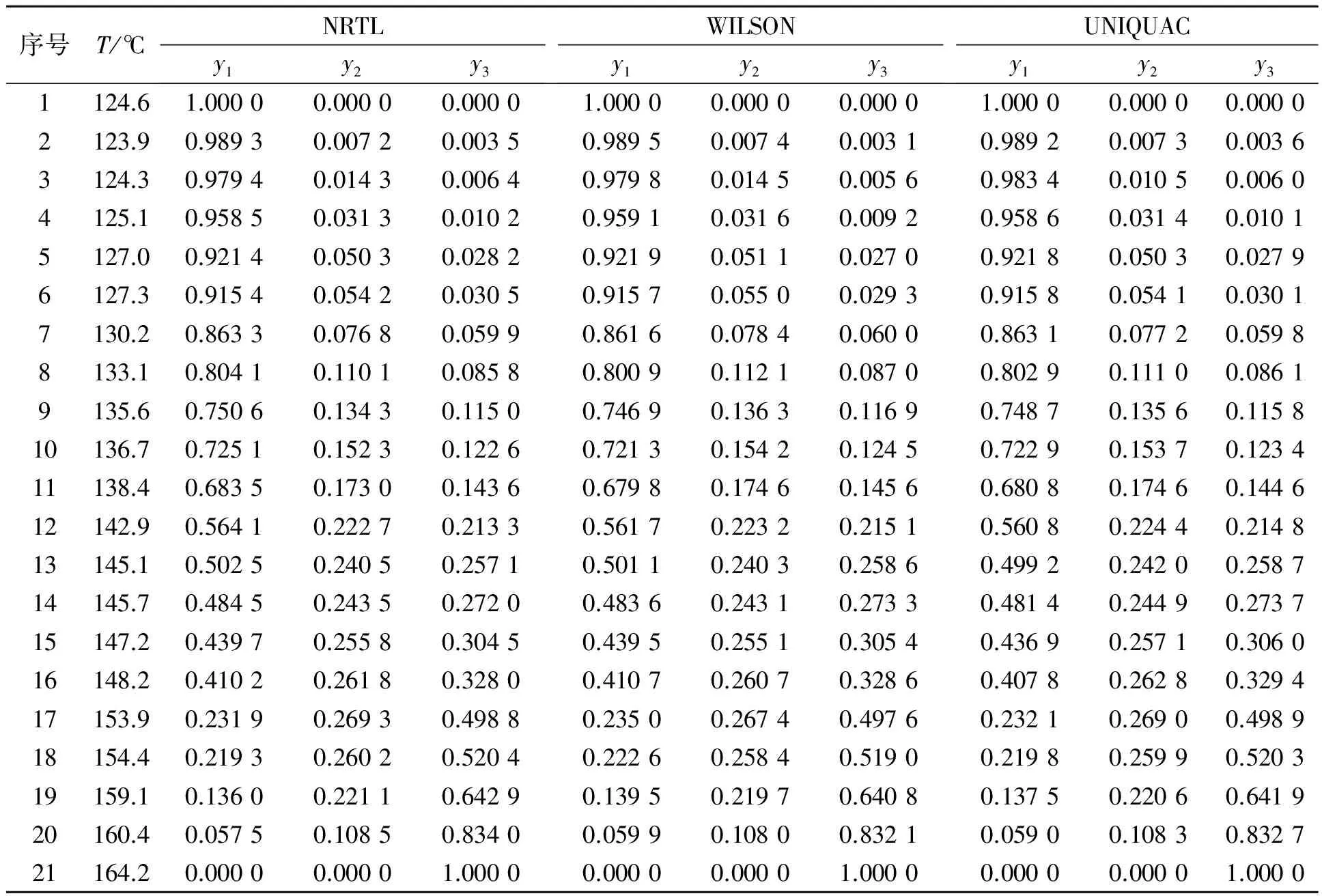
表5 6.67 kPa下乙二醇(1)-1,4-丁二醇(2)-二乙二醇(3)三元气相预测数据

表6 6.67 kPa下三元体系实验数据与预测数据比较
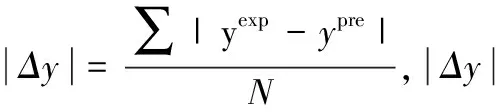
由表6可知,实验检测数据与模拟结果之间最大绝对误差为0.012 6,最大相对误差为5.326%.其中,乙二醇与1,4-丁二醇检测数据与模拟结果之间吻合度高于二乙二醇,这是由于在气相组分中重组分相对较少,因此较小的绝对误差就会引起其相对误差较大.但是,3种模型对于乙二醇-1,4-丁二醇-二乙二醇三元物系都有较好的适用性,模拟结果并无明显差异,其结果均可以认为满足工程分离设计的要求.
由实验数据绘制6.67 kPa下乙二醇-1,4-丁二醇-二乙二醇三元物系的气液平衡相图见图2.
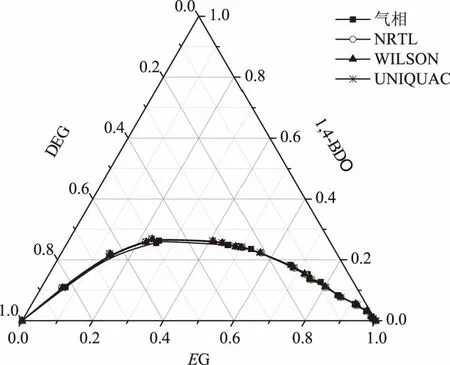
图2 6.67 kPa下乙二醇-1,4-丁二醇-二
4 结论
(1)实验测定了6.67 kPa下乙二醇-1,4-丁二醇-二乙二醇三元物系的气液平衡数据,与工业实际生产中使用压力比较接近,丰富了化工设计基础数据,具有一定的参考价值,可以认为满足工程上分离设计的要求.
(2)分别采用了NRTL、WILSON以及UNIQUAC模型对实验数据进行了关联,发现3种模型对实验所用三元物系适用性并无明显差异,实验数据与3种模型模拟数据之间吻合度都较高,说明3种模型都能很好的适用于该物系.
符号说明:
x——液相质量分数;aij,bij,cij,dij,eij,fij——模型参数;
y——气相质量分数;σ——偏差;
F——目标函数;Δ——偏差;
T——温度,℃;||——绝对值;
上标下标
exp——实验值;i,j——组分;
pre——预测值.
[1] 黄格省,李振宇,李顶杰.石油和煤生产乙二醇技术现状及产业前景分析[J].化工进展,2011,30(7):1461-1465.
[2] 何立,肖含,李应成.乙二醇合成技术研究进展[J].工业催化,2006,14(6):11-15.
[3] 周张锋,李兆基,潘鹏斌.煤制乙二醇技术进展[J].化工进展,2010,29(11):2003-2009.
[4] 孙玉净,于春梅.我国煤制乙二醇产业化现状与前景[J].化学工业,2012,30(1):49-52.
[5] 陈卫航,李清亚,蒋元力.乙二醇-1,4-丁二醇二元物系6.67kPa下汽液平衡研究[J].高校化学工程学报,2015, 29(1):238-241.
[6] 陈军航,陈卫航,蒋元力.真空下1,2-丁二醇-乙二醇二元体系汽液平衡数据的测定及关联[J].天然气化工,2013,38(4):55-59.
[7] 陈卫航,陈军航,蒋元力,等.真空下1,2-丙二醇-乙二醇二元体系汽液平衡研究[J].郑州大学学报(工学版),2013,34(6):36-39.
[8] GORALl M.Derivation of Wilson equation for GE from association models[J].Fluid phase equilibria,1995,106(1):11-16.
[9]NAGATA I.Representation of ternary liquid-liquid equilibria by means of modified from the Wilson equation[J].Thermochemical acta,1995,249(1/2):75-87.
[10]RENON H,PRAUSNITZ J M.Local compositions in thermodynamic excess functions for liquid mixtures[J].AIChE J,1968,14(1):135-144.
[11]ABRAMS D S,PRAUSNITZ J M.Statistical thermodynamics of liquid mixtures: a new expression for the excess Gibbs energy of partly or completely miscible systems[J]. AIChE J, 1975,21(1):116-118.
[12]WISNIEWSKA-GOCOWSKA B,MAIANOWSKI S K.A new modification of the UNIQUAC equation including temperature dependent parameters[J].Fluidphase equilibria,2001,180(1/2):103-113.
Vapor-Liquid Equilibrium for Ternary System of Ethylene Glycol-1, 4-Butylene Glycol and Diethylene Glycol
CHEN Weihang1, LI Yien1,ZHANG Jie1, JIANG Yuanli2, WANG Xunqiu1
(1.School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou 450001, China; 2.Henan Energy Chemical Industry Group Co., Ltd, Zhengzhou 450046, China)
In this study, isobaric vapor-liquid equilibria (VLE) data for the ternary system of Ethyleneglycol, 1,4-Butylene glycol and Diethylene glycol were measured at 6.67 kPa. The experimental data were correlated by the widely used NRTL, UNIQUAC, and Wilson models, and the results showed that the maximum average relative error between the experimental data and the predicted data was 5.3262%, which could meet the requirement of separation engineering.
producing glycol by coal;ternary VLE;NRTL equation;WILSON equation; UNIQUAC equation
2016-05-16;
2016-07-20
河南省重大科技专项(豫科计【2011】6号)
陈卫航(1957—),女,湖南湘潭人,郑州大学教授,主要从事化学分离工程研究,E-mail:cwh295@126.com.
1671-6833(2016)06-0019-05
TQ 013.1;O 642.42
A
10.13705/j.issn.1671-6833.2016.06.017
