超宽带引信取样脉冲宽度与相关接收输出信号幅度关系研究

李萌， 黄忠华

(北京理工大学 机电学院, 北京 100081)



超宽带引信取样脉冲宽度与相关接收输出信号幅度关系研究

李萌， 黄忠华

(北京理工大学 机电学院, 北京 100081)

超宽带无线电引信接收机基于相关接收原理获取预设炸高处的目标回波信号，回波信号与经过延迟的取样脉冲信号进行相关运算得到引信接收机输出信号。优化取样脉冲宽度可以提高超宽带引信探测灵敏度。根据超宽带引信相关接收原理，建立超宽带引信相关接收数学模型，分析取样脉冲宽度与相关接收函数幅值的关系。发射脉冲宽度分别为50 ps、100 ps、200 ps时对引信相关接收输出信号进行仿真，仿真结果表明取样脉冲宽度与发射脉冲宽度相等时引信相关接收输出信号幅度最大；通过实验结果验证了该理论模型的正确性。研究结果适用于超宽带引信接收机优化设计。

兵器科学与技术； 引信； 超宽带； 相关接收； 时域多普勒

0 引言

超宽带无线电引信接收机基于相关接收原理获取预设炸高处的目标回波信号，回波信号与经过延迟的取样脉冲信号进行相关运算得到引信接收机输出信号[1-4]。优化取样脉冲宽度可以提高超宽带引信探测灵敏度，采用不同宽度的取样脉冲信号时引信接收机输出信号幅度发生改变，研究取样脉冲宽度与引信相关接收输出信号幅值的关系，对超宽带无线电引信接收机优化设计具有指导意义。国内外对取样脉冲宽度研究较少，文献[4]针对指数型取样积分电路通过电路模型研究取样脉冲宽度对超宽带引信回波信噪比影响，仅得到取样脉冲不应过宽或过窄的结果。

本文通过分析超宽带引信接收回波信号的过程建立超宽带引信相关接收数学模型，通过建立的超宽带引信相关接收函数仿真分析取样脉冲宽度与引信输出信号幅值的关系，完善超宽带无线电引信的理论，为引信接收机优化设计奠定理论基础。

1 超宽带引信相关接收原理

基于取样积分[5-6]的超宽带无线电引信相关接收原理如图1所示，接收天线输出信号作为引信相关接收机输入信号，通过取样脉冲控制的取样门实现取样过程，取样后的信号经过积分得到相关接收输出信号。

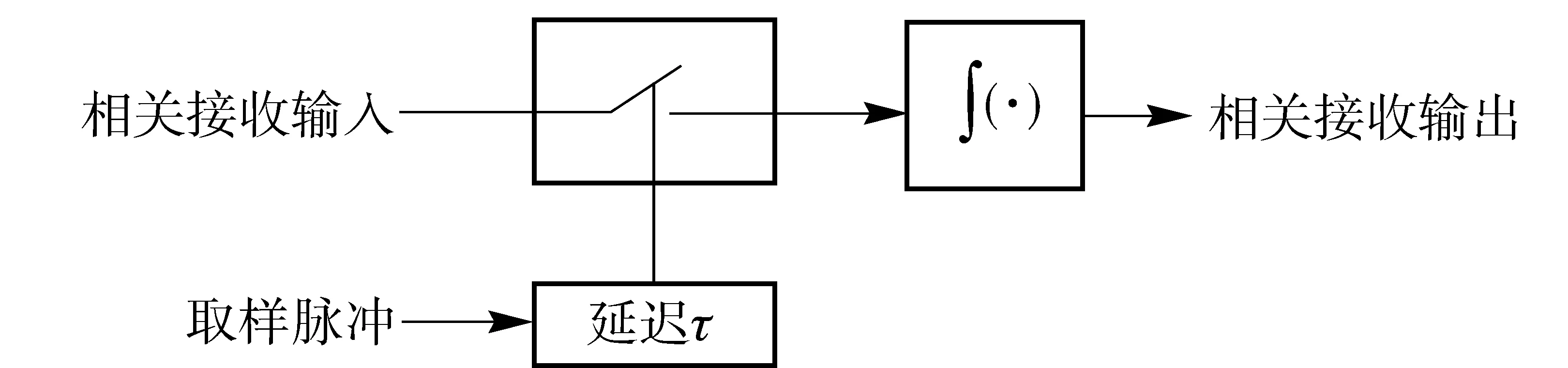
图1 相关接收原理框图Fig.1 Block diagram of correlation receiving principle

由图1可以看出，超宽带引信相关接收过程实质为取样脉冲与相关接收输入信号进行相关运算，表示为

(1)

式中：r(t)为取样脉冲；gt(t)为相关接收输入脉冲序列。

将取样脉冲数量和宽度、脉冲重复周期、引信对地速度等参数代入引信相关接收表达式中建立完整的超宽带引信相关接收数学模型。

2 超宽带引信相关接收过程的取样脉冲数量

超宽带引信的取样脉冲序列表示为

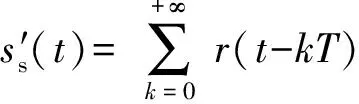
(2)

式中：T为发射脉冲的重复周期。

根据时域多普勒效应[7-10]，在引信接近地面的运动过程中接收脉冲信号重复周期小于发射脉冲的重复周期，表示为

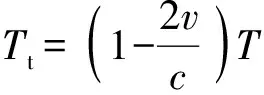
(3)

式中：Tt为回波信号重复周期；v为引信相对地面的运动速度；c为电磁波速度。

超宽带引信接收的回波脉冲序列表示为

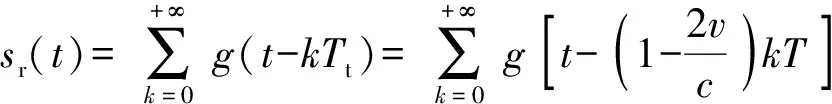
(4)

式中：g(t)为单个回波脉冲信号。

超宽带引信取样脉冲信号与回波脉冲信号之间的时移关系如图2所示。

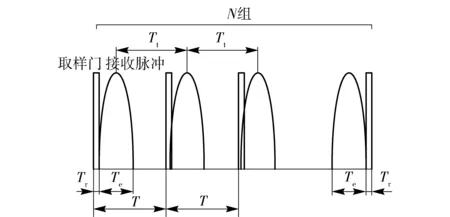
图2 回波脉冲相对取样脉冲的时移Fig.2 Time shifting of echo pulse relative to sampling pulse

根据图2示意的时移关系可得

(N-1)T=(N-1)Tt+Tr+Te=

(5)

式中：N为取样脉冲个数；Tr为取样脉冲宽度；Te为接收的回波脉冲信号宽度。

整理(5)式计算可得

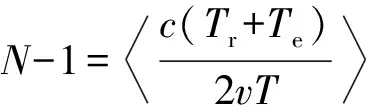
N-1= c(Tr+Te)2vT

(6)

式中：〈·〉表示取整符号。

根据(6)式将(2)式和(4)式改写为

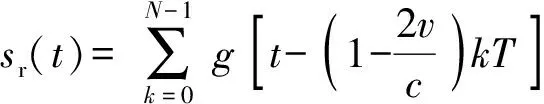
(7)

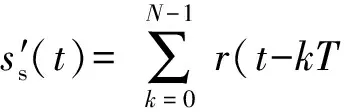
(8)

3 超宽带引信相关接收数学模型

根据图3所示取样脉冲与回波脉冲信号相关过程，回波脉冲通过取样门经过的区间为

(9)

图3 取样脉冲与回波脉冲相关过程Fig.3 Correlated process of sampling pulse and echo pulse

超宽带引信在图2所示的区间内完成取样脉冲与回波脉冲信号的相关运算，引信预定炸高ϑ0表示为

(10)

式中:τ0为取样脉冲信号的预定延迟时间。

图2所示的相关接收区间表示为

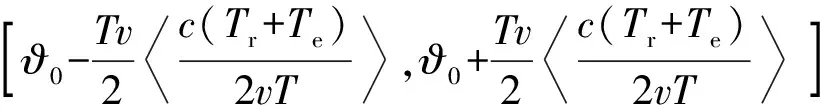
[ϑ0-Tv2 c(Tr+Te)2vT ，ϑ0+Tv2 c(Tr+Te)2vT ]

.

(11)

(11)式表示的区间即为取样脉冲与回波脉冲信号相关运算过程中引信距离地面的高度范围，用引信距地面高度表示相关运算的取值范围：

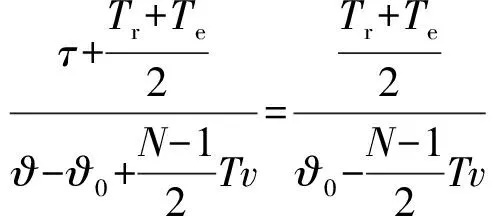
(12)

整理(12)式得

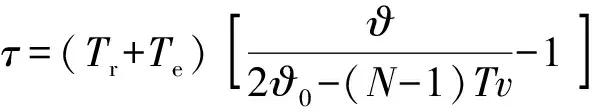
(13)

将(13)式代入(1)式得到引信相关接收函数表达式为

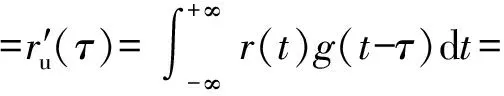
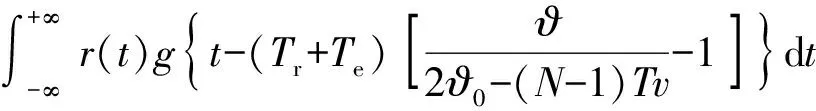
(14)

式中：ϑ

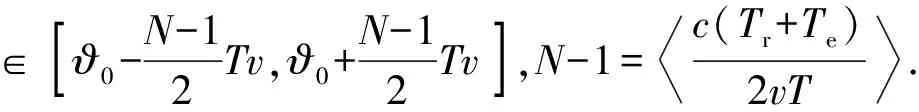
∈[ϑ0-N-12Tv，ϑ0+N-12Tv]，N-1= c(Tr+Te)2vT ．

4 取样脉冲宽度与相关接收函数幅值的关系

采用高斯2阶导函数模拟超宽带引信发射的窄脉冲信号[11]，高斯2阶导函数表达式为

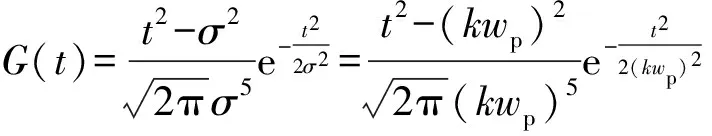
(15)

式中：σ为高斯信号的均方差，控制了脉冲的有效宽度，也称为脉宽因子，可表示为σ=kwp，wp为脉冲宽度，k为脉宽因子系数。脉冲宽度分别为50 ps、100 ps和200 ps的窄脉冲幅度归一化时域波形如图4所示。

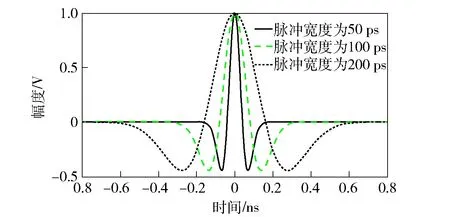
图4 超宽带窄脉冲时域波形Fig.4 Time domain waveform of UWB narrow pulse

超宽带引信发射信号经过发射天线、地面散射和接收天线后得到的回波信号表示为

(16)

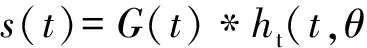
(17)

式中：MeNe表示分解的单元数量；Rq为引信到地面单元的距离。

为简化计算，忽略天线在不同辐射方向上辐射波形的不同，弹体落角为90°，仿真得到引信发射信号脉宽为200 ps，引信对地速度200 m/s，距离地面6 m的回波信号如图5所示。

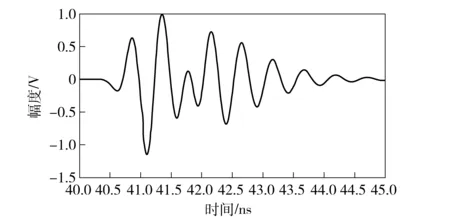
图5 地面目标引信回波信号Fig.5 UWB fuze echo signal from ground target

图6 引信相关接收函数输出信号Fig.6 UWB fuze output signal of correlation receiving function

取样脉冲信号r(t)用高斯2阶导函数表示，将(17)式代入(14)式得引信相关接收函数表达式为

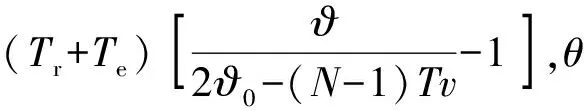
(18)

式中：ϑ

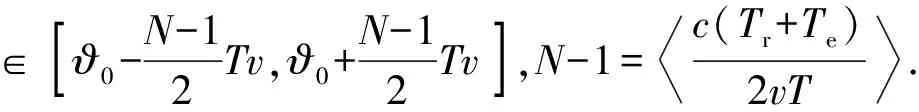
∈[ϑ0-N-12Tv，ϑ0+N-12Tv]，N-1= c(Tr+Te)2vT ．

引信发射信号为200 ps脉宽的高斯2阶导函数，取样脉冲信号选用不同脉宽的高斯2阶导函数时引信相关接收函数输出信号如图6所示。

取样脉冲宽度与引信相关接收函数输出信号幅度关系曲线如图7所示。

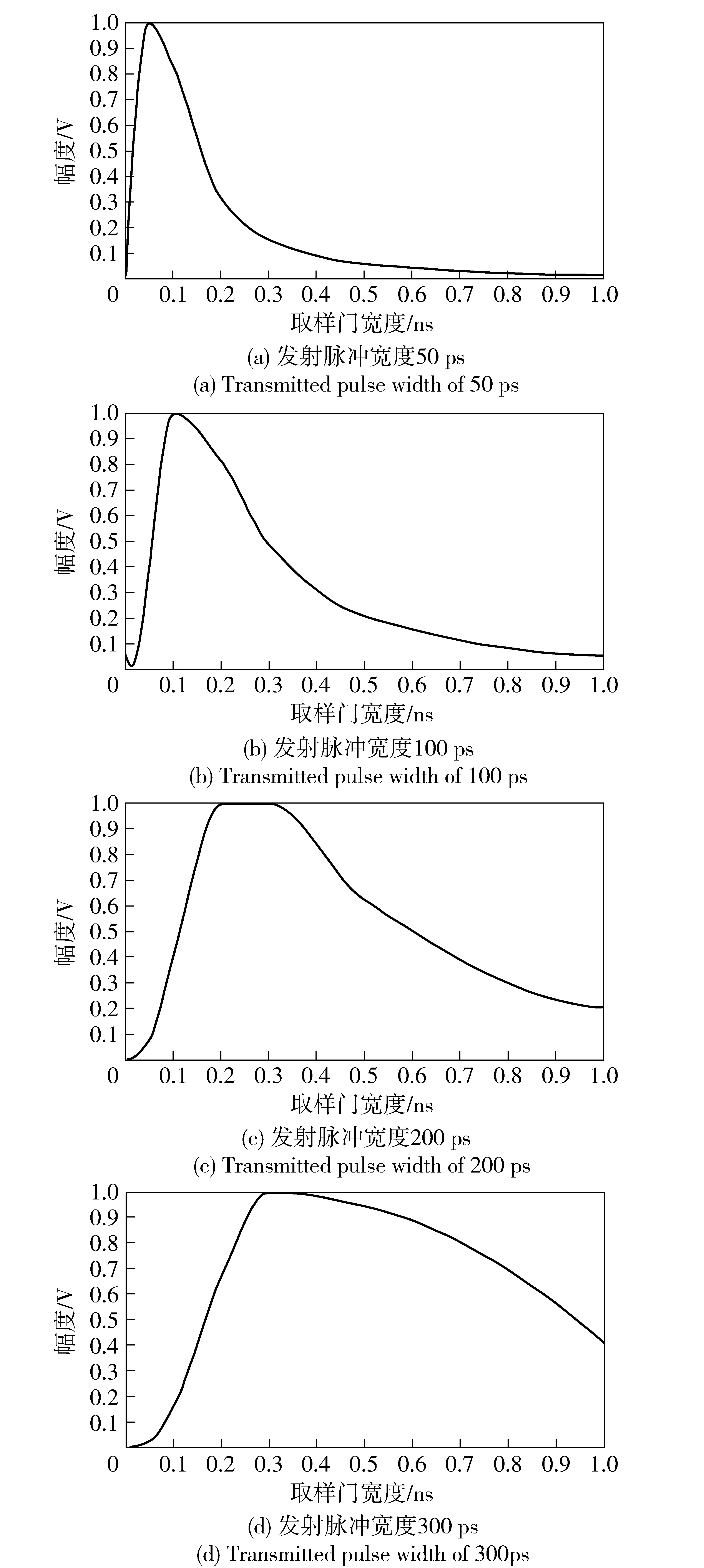
图7 取样脉冲宽度与相关接收输出信号幅度关系曲线Fig.7 Relation curve between sampling pulse width and amplitude of correlation received output signals

如图6所示通过数值仿真得到超宽带引信相关接收输出信号，选取发射脉冲宽度分别为50 ps、100 ps、200 ps和300 ps时绘制取样脉冲宽度从0到1 ns对应的超宽带引信相关接收输出信号幅度曲线如图7所示，可以看出取样脉冲宽度与发射脉冲宽度相等时引信相关接收输出信号幅度取得最大值。

5 实验结果

引信预设炸高6 m，采用推板法测试超宽带引信相关接收机输出信号，敷铜推板尺寸为76 cm×77 cm，选取不同脉宽的取样脉冲进行实验测试，取样脉宽分别为489 ps、511 ps和555 ps引信相关接收机输出信号如图8所示。

如图8所示取样脉宽分别为489 ps、511 ps和555 ps引信相关接收机输出信号幅度依次为4.7 V、7.5 V和5.5 V，引信发射脉冲宽度为502 ps，实验结果验证仿真方法正确性，表明取样脉宽等于发射脉宽引信相关接收机输出信号幅度较大。

6 结论

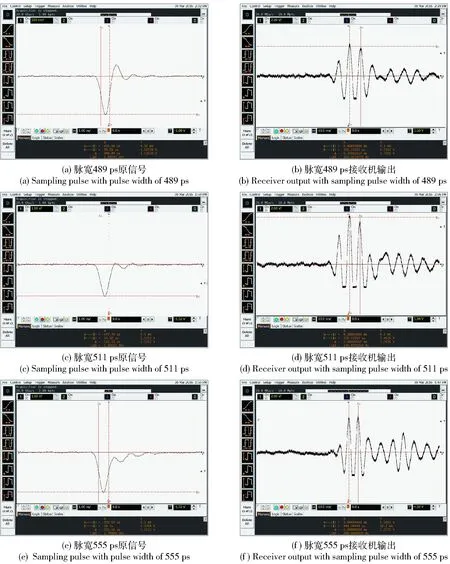
图8 引信相关接收机输出信号Fig.8 Fuze correlation receiver output signals

根据超宽带引信相关接收原理建立超宽带引信相关接收数学模型，分析取样脉冲宽度与相关接收函数幅值的关系。发射脉冲宽度分别为50 ps、100 ps、200 ps时对引信相关接收输出信号进行仿真，利用高斯2阶导函数模拟超宽带引信发射窄脉冲信号，仿真结果表明取样脉冲宽度与发射脉冲宽度相等时引信相关接收输出信号幅度最大。通过实验结果验证理论模型正确性，研究结果适用于超宽带引信接收机优化设计。

References)

[1] Chen S, Zhao H C, Zhang S N. Study of ultra-wideband fuze signal processing method based on wavelet transform[J]. IET Radar, Sonar & Navigation, 2014, 8(3):167-172.

[2] Wang S G, Wei G H, Liu H B. Test research on UWB effects and mechanism of radio fuze[C]∥4th Asia-Pacific Conference on Environmental Electromagnetics. Dalian, China:IEEE, 2006.

[3] Li Z B. Implementation and development of compact UWB proximity fuze sensor system[C]∥2011 International Conference on Computational Problem-Solving. Chengdu, China:IEEE, 2011.

[4] 宋宝军, 付红卫, 王欣. 取样脉冲宽度对冲激引信回波信噪比的影响[J]. 探测与控制学报, 2012, 34(5):11-15. SONG Bao-jun, FU Hong-wei, WANG Xin. Effect of sampling impulse width on impulse radar fuze echo SNR[J]. Journal of Detection and Control, 2012, 34(5):11-15.(in Chinese)

[5] Wu Y, Sepehri N. Interpolation of band limited signals from uniform or non-uniform integral samples[J]. Electronics Letters, 2011, 47(1):53-55.

[6] Holt A G J, Hill J J, Linggard R. Integral sampling[J]. Proceedings of the IEEE, 1973, 61(5):679-680.

[7] Ubolkosold P, Knedlik S, Loffeld O. A method to extend the estimation range of the existing time-domain Doppler centroid estimators[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(2):185-188.

[8] Wang Y Y, Fish P J. Arterial Doppler signal simulation by time domain processing[J]. European Journal of Ultrasound Engineering, 1996, 3(1):71-81.

[9] Barber W D, Eberhard J W, Karr S G. A new time domain technique for velocity measurements using Doppler ultrasound[J]. IEEE Transactions on Biomedical Engineering, 1985, 32(3):213-229.

[10] Vaitkus P J, Cobbold R C. A new time-domain narrowband velocity estimation technique for Doppler ultrasound flow imaging.

I. Theory [J]. IEEE Transactions on Ultrasonics, Ferroelec-trics, and Frequency Control, 1998, 45(4):939-229.

[11] YU X F, Gao M, Li W Z. Computer simulation design of a UWB proximity fuze impulser based on SRD[C]∥ 2009 WRI World Congress on Computer Science and Information Engineering. Los Angeles, CA, US:IEEE, 2009:141-143.

[12] 沈磊, 黄忠华. 超宽带无线电引信回波信号建模与仿真[J]. 兵工学报, 2015, 36(5):795-800. SHEN Lei, HUANG Zhong-hua. Modeling and simulation of echo signal of UWB radio fuze[J]. Acta Armamentarii, 2015, 36(5):795-800.(in Chinese)

Research on Relation between Sampling Pulse Width and Output Signal Amplitude for Ultra-wideband Radio Fuze

LI Meng， HUANG Zhong-hua

(School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081，China)

Ultra-wide bandwidth (UWB) radio fuze receiver receives a target echo signal based on a correlation receiving principle. The signals from fuze receiver are obtained by the correlation calculation of echo signal and delayed sampling pulse signal. The sampling pulse width can be optimized to increase the detection sensitivity of UWB fuze. A correlation receiving mathematical model of UWB fuze is established based on the correlation receiving theory, and the relationship between the sampling pulse width and the amplitude correlation receiver function is analyzed. The received output signals are simulated when transmitted pulse width is 50 ps, 100 ps and 200 ps. The simulated results show that the fuze-received output signal has the maximum amplitude when the sampling pulse width is the same as the transmitted pulse width.

ordnance science and technology; fuze; ultra-wide bandwidth; correlation receiving; time-domain Doppler

2016-04-18

总装备部预先研究项目(62201040601)

李萌(1986—)，男，博士研究生。E-mail: phdmeng@bit.edu.cn； 黄忠华(1965—)，男，副教授，博士生导师。E-mail:huangzh@bit.edu.cn

TJ43+4.1

A

1000-1093(2016)11-1989-06

10.3969/j.issn.1000-1093.2016.11.004