基于Radon变换的滤波反投影重建算法研究

张晓瑞

摘要：层析成像技术目前在生物学等领域广泛应用，而Radon变换是投影重建的数学理论基础。文中简单介绍了Radon变换的基本原理，重点介绍了滤波反投影重建算法，尤其是滤波函数的选取，并对重建结果进行了比较。

关键词：图像重建；Radon变换；滤波反投影

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2016）27-0259-03

1 引言

层析成像技术在医疗、 生物等领域具有广泛应用。图像重建是指通过物体外部测量数据，经过处理从而获得物体的形状信息的技术。开始主要应用在放射医疗设备中，用于人体各部分图像的显示，即计算机断层摄影技术，简称CT技术，后来逐渐在许多领域获得应用。

透射CT的理论基础是投影重建。而Radon变换是投影重建的数学基础，它是数学家J.Radon提出来的，被广泛应用于医学、分子生物学等领域，迄今为止，人们已研究出基于Radon变换的多种重建方法。文中重点介绍的滤波反投影算法也是基于Radon变换的一种变换法重建，目前在CT系统中应用非常广泛。滤波反投影算法的比较重要的是滤波函数的选取。

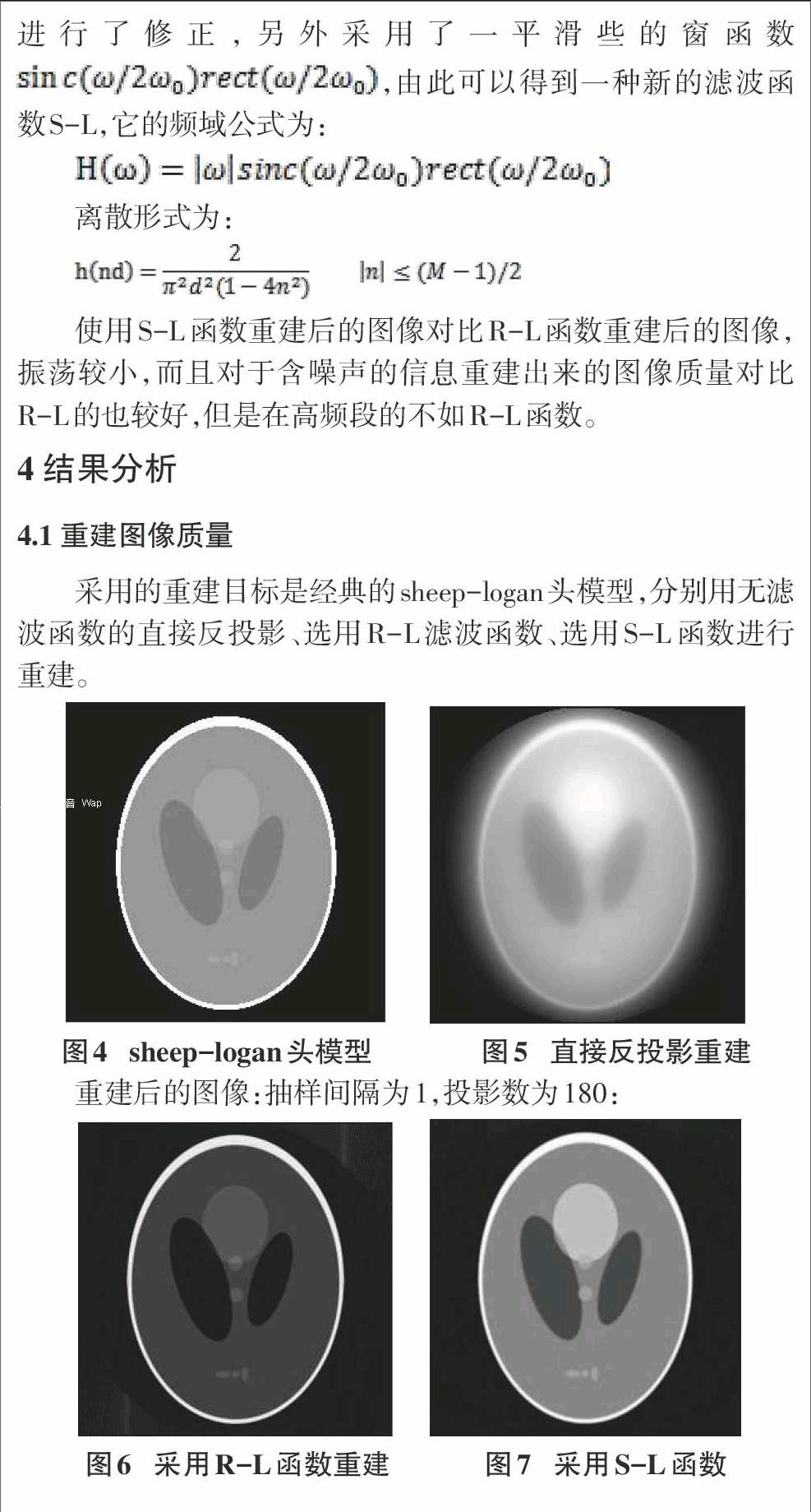
4.3 结果分析

（1）图像比较：直接反投影算法的重构对像的边缘很不明显，有阴影。滤波反投影算法重构对象相对来说清晰很多，没有阴影。

（2）重建时间对比：滤波反投影算法的重构时间较长，因为多了卷积、滤波这个步骤，使重构时间加长。不过在实际应用中，这个时间增加不会有很大影响，但是质量却明显变好，所以，实际应用中一般采用此方法。

5 总结

滤波反投影法是重构图像基本常用的算法，也是其他多种算法的基础。在医学CT 等领域中的应用较为广泛。但是这种算法的关键是选取的何种滤波函数，会直接影响重建图像的质量。除了滤波函数对图像质量有着较大的影响外，根据抽样定理，投影数和抽样间距均对重建图像的质量有影响[2]。以后的工作中也应对抽样间距进行研究。

参考文献：

[1] 高欣.新型迭代图像重建算法的理论研究与实现[D].浙江：浙江大学，2004.

[2] 刘晓.工业CT图像重建算法的计算机模拟研究[D].四川：四川大学，2004.

[3] 莫华，龙莉玲. X-CT图像重建的卷积反投影图解法[J].中国医学物理学杂志，1999，16（3）：143-145.