基于稀疏优化算法的视频运动分割
2016-12-15冯思桐武坚
冯思桐+武坚

摘要:该文提出一种基于子空间模型分割视频中多个运动目标的方法。实际视频序列中提取的特征点是复杂的高维数据,本文结合现有文献,首次提出使用稀疏主成分分析(SPCA)算法降维,将原始高维数据投影到一个具有稀疏表示的低维空间,在此基础上,提出基于特征角的“稀疏近邻”估计方法得到相似度矩阵,从而获得最终的子空间聚类结果。将该文提出的方法应用到视频序列中,并与现有的运动分割的算法进行比较。实验结果表明,本文提出的方法可以准确对视频中不同运动的物体进行分类,并在精度和运算速度方面与其他算法相比都有很大的提高。
关键词:视频分割;稀疏优化;子空间模型
中图分类号:TP302 文献标识码:A 文章编号:1009-3044(2016)27-0139-05
1 介绍
视频的运动分割,旨在从视频序列中分解出多个连续移动的不同物体。将不同运动物体的信息从视频中提取出来之后,可以做很多后续的研究,如异常行为分析或者运动物体的追踪。近几年,基于特征点轨迹聚类的视频运动分割问题是主要的研究方向,首先对提取的实际视频序列进行预处理获得特征点轨迹,如KLT[1],SIFT[2]或者SURF[3]等特征点提取算法,基于不同的运动目标对特征点轨迹集合进行聚类。但是长视频序列中提取和跟踪的特征点集合往往是高维复杂的大数据,需要寻求一种高精度并能快速对高维复杂数据进行分类的方法。基于子空间模型下的运动分割,是现如今被普遍研究的分类方法。子空间模型下分类的基本思想是,从视频序列中提取到的每一组特征点轨迹都认为其点集合共同构建了一个子空间,那么不同特征点集合的聚类问题,即转化为对一组子空间集合进行聚类的问题。
本文基于LSA聚类算法[7]以及稀疏子空间聚类算法(SSC)[6]的思想,提出一种基于稀疏优化对子空间进行聚类的新方法。实验结果表示,本文所提出的方法,可以有效且快速地分类实际视频中的不同运动目标。
2 基于子空间模型下的运动分割
2.1 子空间聚类模型
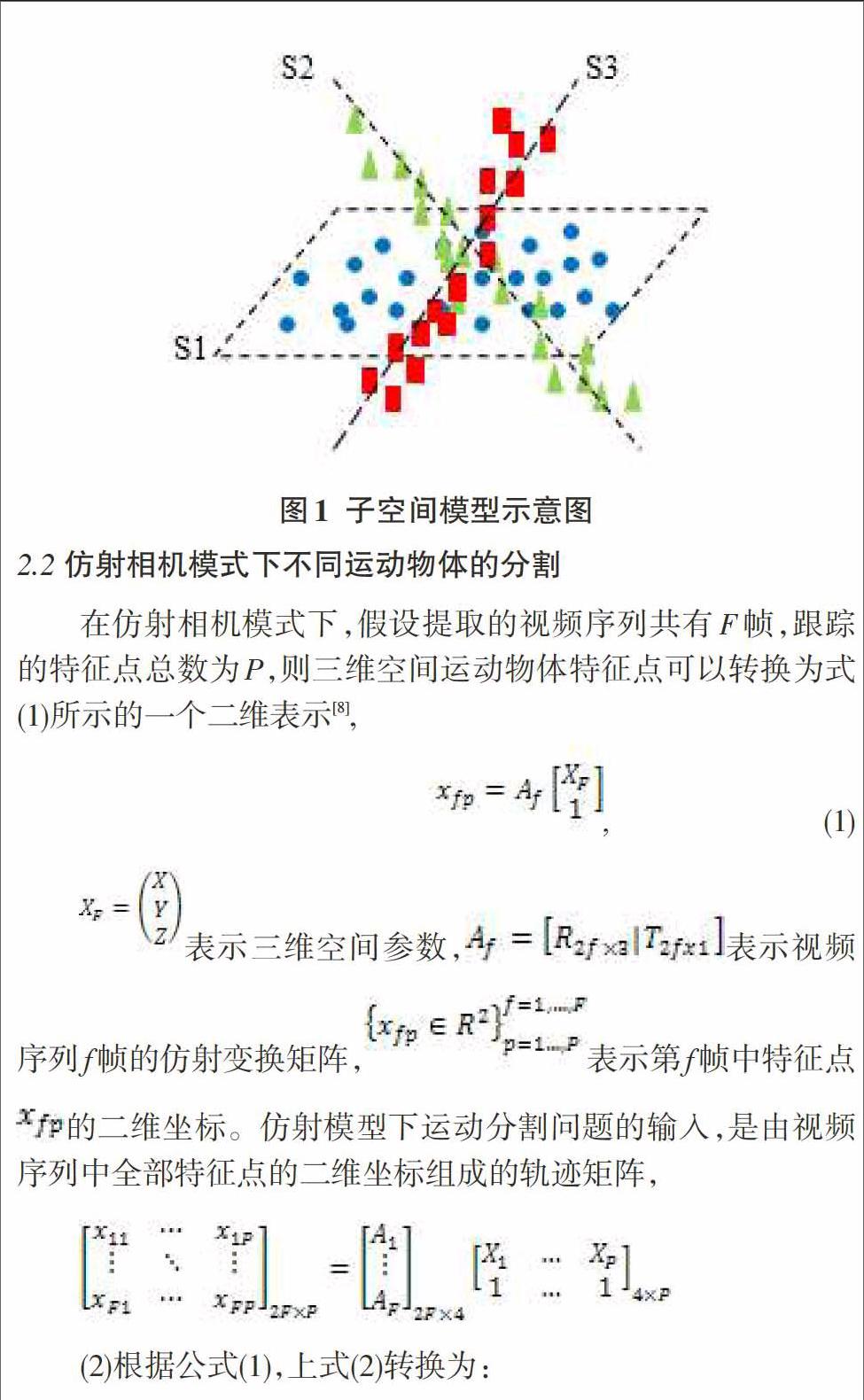
对特征点集合组成的高维数据聚类,基于子空间的模型,首先需要获得高维数据的低维表示,而这个低维表示能够保持原大数据矩阵的本质特征。假设,将原高维数据的低维投影看作一个变换后的“全局子空间”,而全局子空间是由不同的更低维度的“本地子空间”相互交叠构成,如图1,三种数据点集合构成三种子空间S1,S2,S3,集合S={ S1,S2,S3}称作全局子空间,S1,S2,S3相对的称作本地子空间。本文中基于子空间模型进行分类的基本思想就是从全局子空间中找出不同的本地子空间,属于同一本地子空间的数据应当被划分到同一类中,即划分为属于同一种运动目标。
4 实验结果与分析
本文实验数据选自标准的视频数据库Hopkins 155数据集[13]。并将本文提出的优化算法与现今其他优秀的运动分割算法进行比较,在分割的过程中,假设所有视频中运动目标的个数已知。
图6,7,8是采用本文所提出算法进行聚类的结果,不同颜色代表不同的运动目标。图6中包含3中运动,红色点代表背景,蓝色和绿色代表两种汽车的运动,图7中包含2种运动,人的手臂以及手上拿的物体分别用红色和绿色进行区分,图8代表了3种物体的运动,红色点代表背景,由图7可知,对于特征点多且复杂的难以区分运动模式,我们所提出的算法可以有效的对不同的运动目标进行区分。为了进一步表明本文所提出算法的优势,我们将从错误率和运算时间与SSC [6], LSA [7], RANSAC [4], GPCA [5], LLMC [14]算法进行对比。
从表1、2、3、4可以得出,我们所提出的算法具有比较好的准确度,虽然相比SSC算法来说准确度略低,但是我们的优化算法与SSC相比加快了运算的速度。
5 总结
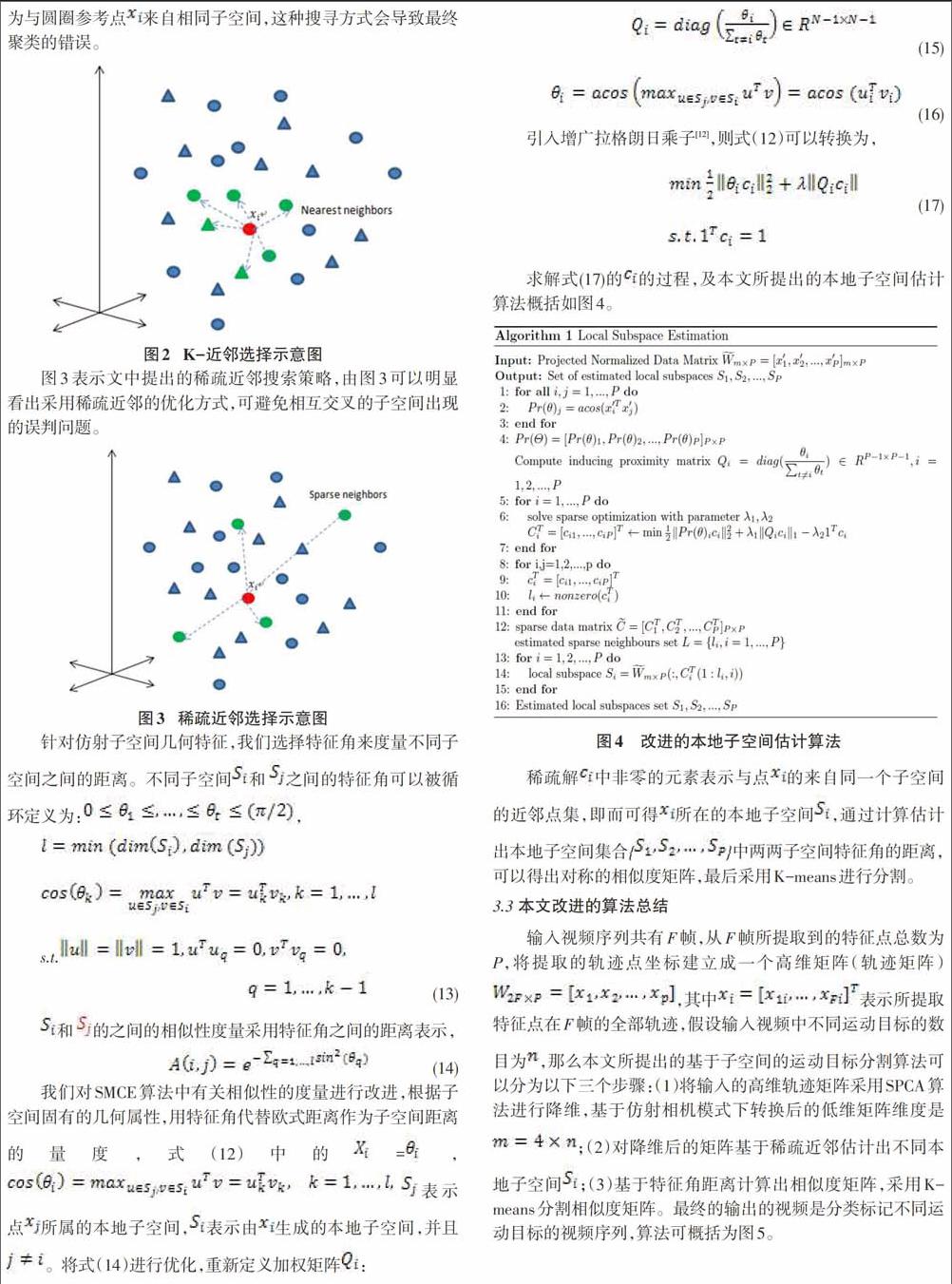
本文提出了一种基于子空间的运动分割优化方法,可以对实际视频序列中不同的运动物体进行有效分类。首先通过SPCA算法[15]将高维数据投影在一个低维的空间上,并且具有少数的非零元素;基于SMCE [9]的思想,对投影后低维空间中不同的子空间进行估计,寻找在低维空间中每一个数据点的稀疏近邻(隶属于同一子空间),将投影后分布于低维空间中的不同子空间分割出来,这种方式相比较LSA算法来说,改善了过度估计和不同子空间相互交叉的问题,大大提高了准确率。与SSC算法相比,运算时间得到提升。在未来的研究中,将对长视频序列中运动目标分割的研究作为主要方向,并侧重数据缺失或不完整轨迹等问题,进一步提升算法的准确性和实用性。
参考文献:
[1] Tomasi C, Kanade T. Detection and tracking of point features. School of Computer Science, Carnegie Mellon Univ. Pittsburgh,1991.
[2] Zhou H, Yuan Y, Shi C. Object tracking using sift features and mean shift.Computer vision and image understanding, (2009,113:345,352.
[3] Bay H, Ess A, Tuytelaars T, Van Gool L.Speeded-up robust features (surf). Computer vision and image understanding, 2008,110:346,359.
[4] Fischler M A, Bolles R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM 1981:24:381,395.
[5] Vidal R, Ma Y, Sastry S.Generalized principal component analysis (gpca). Pattern Analysis and Machine Intelligence, IEEE Transactions,2005,27:1945,1959.
[6] Elhamifar E, Vidal R. Sparse subspace clustering. In: Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on IEEE,2009:2790,2797.
[7] Yan J, PollefeysM.A general framework for motion segmentation: Independent,articulated, rigid, non-rigid, degenerate and non-degenerate. In: Computer Vision ECCV 2006. Springer (2006,94:106.
[8] Hartley R, Zisserman A.Multiple View Geometry in Computer Vision. 2 edn. Cambridge University Press, New York, NY, USA.2003.
[9] Elhamifar E, Vidal R. Sparse manifold clustering and embedding. In: NIPS,2011:55,63.
[10] Journ_ee , Nesterov , Richt_arik , Sepulchre . Generalized power method for sparse principal component analysis. The Journal of Machine Learning Research,2010, 11:517,553.
[11] dAspremont A, El Ghaoui L, Jordan M I, Lanckriet G R.A direct formulation for sparse pca using semidefinite programming. In: NIPS. Volume,2004, 16.:41,48.
[12] Tibshirani R.Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological,1996:267,288
[13] Tron R, Vidal R.A benchmark for the comparison of 3-d motion segmentation algorithms. In: Computer Vision and Pattern Recognition, 2007. CVPR07. IEEE Conference on, IEEE,2007:1,8.
[14] Goh A, Vidal R.Segmenting motions of di_erent types by unsupervised manifold clustering. In: Computer Vision and Pattern Recognition, 2007. CVPR07. IEEE Conference on, IEEE,2007:1,6.
[15] Zou H, Hastie T, Tibshirani R. Sparse principal component analysis. Journal of computational and graphical statistics,2006,15:265,286.
