谈初中数学新知教学的创新方式

何菲

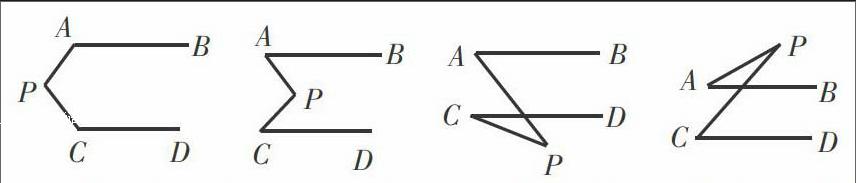
[摘 要]想要实现初中阶段的优质数学教学，在合理安排教学内容的同时，还需要从教学方式上不断进行创新，这样方能双管齐下，全面推进.本文从教学创新的基本理论与实践经验出发，分阶段提出若干创新对策.

[关键词]初中数学 创新方式

[中图分类号]G633.6[文献标识码]A[文章编号] 16746058（2016）260028

数学，无论是知识的运用，还是内容的理解，总是会随着环境与思维的变化而变化.这种灵活性正是数学学习的魅力所在.数学知识内容的每一次变化，都是在以一个全新的面貌加以呈现，想要时刻与之保持同步，妥善应对，就需要学生具备一个动态、创新的头脑，与数学一起灵动向前.为了有效培养学生的创新意识，创新的教学方式也就成为数学课堂的必需.作为数学思维建立形成的基础阶段，初中数学课堂更呼唤这种开拓的教学视野与创新方式.

一、课前提出创新问题，激活学习热情

数学教学的创新从教学正式开始之前就已经启动了.为了实现高效的主体知识教学，教师经常会在课堂教学一开始先设置一个简短的知识导入环节，将学生们的思维从课外衔接到课内.也正是这个看似转瞬即逝的小动作，为教学方式创新提供了一个宝贵的切入点.如果能够抓住这个时机一改往日的常规导入途径，将会给学生焕然一新的感觉.

例如，在对正多边形的内容进行教学时，我并没有直接将理论内容铺开，而是先向大家提出了这样一个问题：现在想要对教室进行装修，重新铺设地砖.那么，你会选择哪一种正多边形的瓷砖呢？起初，大家大多从美观的角度出发，认为正三角形、正四边形、正五边形等等都是可以的.可有的学生画图模拟了一下，发现并不是每种多边形瓷砖都可以将地面铺满的.这便引发了大家的热烈思考，学生们纷纷期待能够总结出正多边形的特点，下面的教学内容也就呼之欲出了.

有的时候，只需要一个简单的变化，就可以让课堂教学以另一种全新的方式推展开来.课程导入环节是学生接触新知的第一步，如果能够抓住这个机会，让学生带着全新的眼光看待新的知识内容，对于接下来的探究热情提升是大有好处的.这是教学创新的开端，更是高效学习的起点.

二、课堂开展创新活动，优化学习效果

新知呈现的效果如何，很大程度上取决于课堂教学是如何推进的.既然需要教学的知识内容是课堂标准所确定的，那么，教师就可以考虑从形式上进行灵活创新，给固定的内容以全新的样貌，学生的接受效果也就完全不同了.在课堂教学过程当中进行教学方式的创新，是教师所要关注的一个重点课题.

例如，在对一元二次方程根与系数的关系内容进行教学时，我先将基本公式、定理加以呈现，然后将学生分组，请大家关于“在方程ax2+bx+c=0（a≠0）中，a、b、c的作用是什么？”的问题开展自由讨论.这种形式给学生们预留出了十分广阔的探索空间.起初，大家的思路还比较局限，只能找到“二次项系数a是否为零决定着方程是否为二次方程”这样的结论.随着彼此之间的启发越发灵活，学生逐渐找到了当“a≠0，c=0时，方程必有一个根为0”、“当a≠0时，b=0，a、c异号，方程两根互为相反数”等更有价值的结论.在这样的创新互动模式下，教学效果得到了显著优化，学生对知识内容的印象更深了，方法运用也更熟练了.

不同于常规形式的知识讲解，笔者在教学实践当中，有意识地加入了许多生动的教学活动.将抽象晦涩的理论内容以具体有趣的课堂活动展现出来，原本单调的数学学习瞬间变得活灵活现.随着学生亲身投入到教学活动当中，大家对于知识内容的感知也更为真切了.

三、课后设置创新练习，延续学习深度

数学教学的创新并不会随着课堂教学的结束而告一段落.想要完成知识的深入理解与全面巩固，高质量的课后练习必须及时跟上.如何衡量这个“高质量”呢？除了练习的内容之外，形式上是否能够被学生欣然接受也是很重要的标准.

例如，在完成了平行线内容的学习后，我为学生设置了这样一个课后练习：已知AB∥CD，点P分别与A、C相连.随着点P位置的不断变化，形成了如下四种图形状态.请分别分析下面四种情况中∠P与∠A和∠C的关系.

同以往一个问题对应一个图形的情况相比，这种练习形式新颖了许多.在变化的图形当中把握不变的平行关系，让学生们得以更加灵活、深入地感悟平行线相关的理论知识.

课后练习是课堂教学的延续与深化.学生在课后练习当中的表现，一方面反映出了大家对于课堂教学的接受效果；另一方面也帮助学生巩固、深化了对于知识方法的理解掌握.优质创新的练习设置，往往能够对教学实效提升起到四两拨千斤的效果.

初中数学的教学，处处都可以成为教师开展创新的入手点.笔者在文中所阐述的，是从教学进行的时间顺序入手.教师还可以按照知识内容的种类或是适用的教学形式进行分类，从另外的视角来加以探索.

（特约编辑 章 强）