创设多元氛围 培养个性潜能

江苏省阜宁县明达初级中学(224400)

陈海燕●



创设多元氛围 培养个性潜能

江苏省阜宁县明达初级中学(224400)

陈海燕●

新课标一直强调指出，学生的数学学习内容应当是富有挑战性的，在探索过程中去发展他们个性.为此，在数学课堂教学中，我们要结合教学内容，创设多元氛围，设计具有现实的、有意义的数学问题，激发同学们学习数学动力，积极引导学生开动脑筋、仔细观察，探究数学新知识和规律，让学生的个性潜能得到充分发展.下面，结合笔者多年教学实践经验谈几点对创设多元氛围，培养个性潜能的认识，以供读者参考.

一、营造变通氛围 培养个性思维

所谓变通就是指有一个对象问题与另一个对象问题或设想问题之间的相似点，而通过另一个问题或设想问题找到解决问题途径.新课程标准强调：人人都能获得必需的数学，不同的人在数学上得到不同的发展.我们教师要及时了解学生个体差异，运用多元方法或手段，去满足学生多样化的学习，要科学的去挖掘学生学习潜能，让学生大胆创新，进行有效地拓宽、挖掘更深、更广的知识，并激励他们主动参与教学活动，去探索运用自己的方式解决问题，去发现问题，发表自己的看法，培养学生良好的学习个性.

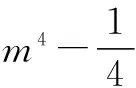
当然，我们要培养各层次学生具有创造个性，只停留在营造变通氛围这个层面上是远远不行的.我们还要做好以下几点 ：1.重视营造民主、宽松、富于创新精神的教学气氛；2.高度重视尊重各层次学生个性，穷尽方法去抓住所有时机，激发他们创新的潜能；3.要注重对学生创造的意识、创新精神培养.这样我们的学生个性思维才能得以彰显.

二、创设多变氛围 激发个性发展

所谓多变氛围就是指根据某一教学内容，进行设计多种变式问题或多元开放问题，进而营造一种变化的气氛.我们教师要根据新课程教学理念，结合学生心理特征，从不同的角度，引导同学们深入思考数学问题的各种演变，尤其是数学变式问题或开放问题，能有效地唤起他们的好奇心和求知欲，能有效地培养学生灵活分析数学问题能力和提升学生发散分析问题能力，也培养学生个性思维能力.

例如：在探索平行四边形教学时，为了激发个性发展，创设多变氛围，运用多媒体展示下列问题：已知四边形MNPQ是平行四边形，A、B分别是边MN、QP上的点，且MA=PB，求证：NB∥QA.

笔者打破以往教学策略，不去直接讲解而是采用开放的方法，让同学们在小组里进行讨论完成(要求：每个人至少一种解法).

由于笔者采用开放策略，同学们在下面学习欲望特别强，积极性高，在小组里进行热烈讨论、交流，各组学生不时脸上露出胜利的微笑，其中第三小组学生周萌萌说出自己的证明思路：从平行四边形的判定定理：“两组对角分别相等的四边形是平行四边形”进行开始，去证四边形NAQB是平行四边形，之后通过平行四边形的定义即得NB//QA.接下来，第六小组学生李荣荣说出自己的证明思路：运用平行四边形的判定定理(两组对边分别相等的四边形是平行四边形)，进行证明四边形NAQB是平行四边形，此时教者可采用让该组学生先口头说明证明过程.紧接着第八小组学生王凯克说出：第一种方法与周萌萌一样方法；第二种方法是根据平行四边形判定定理(一组对边平行且相等的四边形是平行四边形)去证得四边形NAQB是平行四边形，不难得到NB∥QA.等等，课堂气氛显得非常活跃.

笔者通过开放的策略，给同学们营造了多变氛围，既巩固了所学过的平行四边形的判定定理与性质定理，也发展了学生个性思维.另外还有利于培养同学们灵活思维，尤其是广阔、变通、创造性等思维，达到锻炼了同学们的发散思维目的，又调动学生学习积极性，并出现进一步探索问题的势头，既遵循合理性思维的规律，又遵循同学们的认识规律，是在学生最近发展区形成理性认识的基础上的第二次提升，是一个质的飞跃.

G

B