振动噪声环境影响下脉搏信号的非线性特性比较

杨 峰, 韩清鹏

(上海电力学院 能源与机械工程学院, 上海 200090)



振动噪声环境影响下脉搏信号的非线性特性比较

杨 峰, 韩清鹏

(上海电力学院 能源与机械工程学院, 上海 200090)

应用代替数据法计算振动噪声环境影响下脉搏信号的混沌特性,根据所得到的几个特征参数值对不同振动噪声环境下的脉搏信号进行非线性特性对比与分析;阐述了基于代替数据法的时间序列的混沌特性计算原理,通过实验测量不同振动噪声参数并计算与之相应的脉搏信号,获得了振动噪声参数对脉搏信号特征参数的数值变化及影响规律.

振动噪声; 脉搏信号; 代替数据法; 特征参数

随着我国汽车制造业的发展及环保意识的提高,人们越来越重视车内振动噪声环境对人体生理特征造成的影响规律.车内噪声主要来源于发动机、进气管、排气管、冷却系统等,在汽车行驶过程中,各种冲击、振动激励、噪声等通过座椅、悬架等车身及壁板部件传递到车辆内部,激发人们感受到振动反射,进而会影响到乘员的心跳、血压、呼吸等生理指标的波动,长此以往甚至会导致各种生理疾病的产生[1-2].

在汽车振动噪声环境下,乘员的心跳或脉搏、血压、体温、心电、脑电、呼吸都具有一定的数值,甚至脑思维活动都有其正常的变化范围.当环境发生变化时,一般心跳和脉搏会变快,呼吸增多,体温增高,血压发生波动,白血球含量增加等.这些用来衡量人体生理指标的各个参量,都表现出不正常的波动.因此,改善汽车内部声学环境,降低车内噪声水平逐渐成为汽车设计与制造业中共同关心的重要问题[3-6].

由于环境影响因素较多,且无确定的规律可寻,加之人体生理系统的复杂性,对汽车减噪系统的设计及研究带来重重困难.因此,选择非线性算法对脉搏信号的混沌特性开展研究,通过对复杂环境影响下(在这里主要讨论振动噪声)脉搏信号的量化对比分析,能够不同程度地促进减噪系统设计的发展.在非线性预测分析的基础上,可以对有色噪声、随机序列和混沌序列进行有效的区分[7-9].

本文通过测量不同振动噪声影响下的实测脉搏信号,分析信号的主波间期序列,并采用代替数据法对数据进行分析计算,通过对应的算法对参数值进行分析比对,探索人体在不同振动噪声影响下其脉搏信号的变化规律.

1 时间序列特征参数计算理论研究

非线性预测法主要包括随机型和混沌型,是在非线性和非平稳时间序列分析预测时间变化的规律,其算法是通过计算预测值与实际值之间的误差,来判断时间序列的类型[10],可采用Takens原理计算特征参数并予以区别量化[7].

1.1 重构相空间

参考Takens原理的设计思路,对测量得到的一维信号时间序列x(n)进行重构,设d维相空间的状态点为:

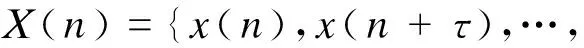
(1)

式中:d——嵌入维数;

1.2 计算拟合集及检验集

通过分割原信号数据点(拟分解为两部分),其中一部分分解为拟合集Nf,剩下的部分分解为检验集Nt.首先通过搜索拟合集内与当前时刻m的状态点X(m)最为邻近的k个状态点(X1(m),X2(m),X3(m),…,Xk(m),m≤n),并计算当前点与X(m)的欧氏正则距离的极值(此处去最小值).在获得当前m时刻的k个状态点后,与下一时刻(m+1)的k个状态点构建相应的二维点对,通过拟合计算,获得预测拟合公式为:

(2)

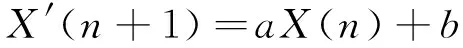
(3)

式中:a,b——拟合系数;X(n+1)——下一时刻预测点.

通过迭代计算,在X(n)状态点遍历整个检验集Nt后,迭代结束,并获得N/2个预测误差ε,ε=X′(n+1)-X(n+1).为保证下一步检验中统计量的正确性,此处还需计算所有误差的平均绝对值.

1.3 生成代替数据集

采用Fourier变换方法,生成新的离散随机数据序列y(n),其中,该序列服从正态分布且长度等参数均与原序列保持不变,并将得到的数据序列按照一定规律重新排序变成新序列z(n),以保证两个序列的秩是不变的.对z(n)进行Fourier变换得P(ω,φ),并采用随机变换方法改变P(ω,φ)的相位,记为P(ω,φs),最后计算序列的逆Fourier变换y′(n).时间序列y′(n)与原数据x(n)保持频谱和自相关函数不变.

1.4 计算虚假设

由于原始数据x(n)的选择具有随机性,这里称为虚假设(Null hypothesis).通过计算数据集差异的显著度,检验对原始数据的虚假设.

(4)

式中:χ——代替数据与原数据的差别;QD——原始数据序列的平均绝对值MAE;us——MAE的均值;σs——MAE的标准差.

如果χ的数值越小,则代表原假设成立,说明具有随机性.现有研究表明,随着χ的增大,混沌性越来越明显,当χ大到使us的分布远离QD时,时间序列满足混沌性要求.与之对应,拒绝虚假设的最大概率P获得较大值.

(5)

式中:erf()——数据序列误差函数,即:

2 不同振动噪声环境下脉搏信号的混沌识别试验

为了研究振动参数对人体生理的应激与变化,对汽车多种行驶工况下(包括匀速行驶、车窗封闭低噪声、开窗高噪声等)车内振动噪声特性进行测量分析,同时记录人体脉搏信号随噪声振动产生的变化.

试验中采用脉搏采集装置连续采集实验对象的脉搏信号.

图1为两种不同工况下座椅振动和车内噪声的测试结果.

图1a和图1b为汽车在平稳行驶时车辆垂直振动参数及车内噪声参数的3D谱阵;图1c和图1d为车辆加速行驶且高噪声工况下座椅垂直振动与车内噪声的3D谱阵.

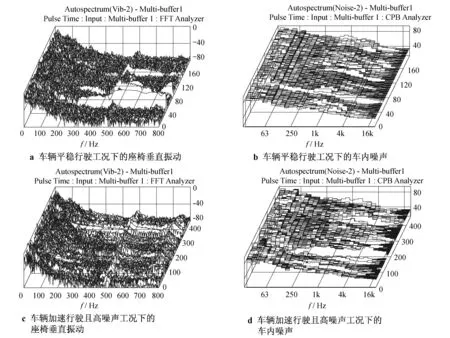
图1 两种不同工况下的座椅振动和车内噪声图谱

采样频率取128 Hz,采样时间取30 s,分别测量上述两种工况下不同乘客的脉搏信号,如图2所示.由图2可知,仅从脉搏波形图来看,很难明确分析振动噪声对脉搏的影响.

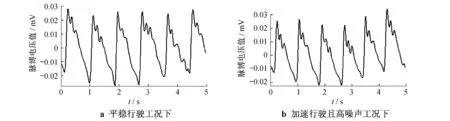
图2 两种振动噪声环境下的实测脉搏信号

对两组实测脉搏信号进行代替数据法分析计算,选取脉搏信号作为原始时间序列x(n),计算分析试验中的128组随机代替数据集.平稳及加速工况下具体特征参数的计算结果如表1所示.

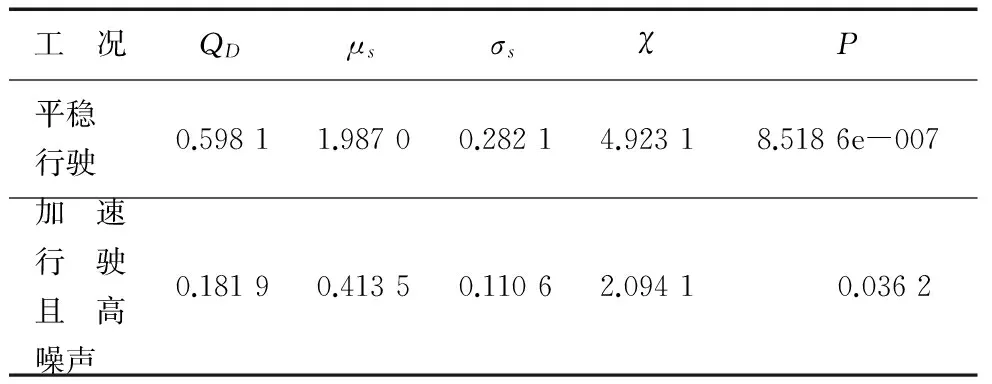
表1 平稳行驶及加速行驶工况下的代替数据法计算数据

由表1可知,两种工况下的P值都远小于0.05,均可以判定为符合混沌特性,且两种工况下的P值具有明显的差异性,即加速工况下P值的数量级远远高于平稳工况下.根据P值的计算结束,从另一个角度分析可知,在平稳行驶时,脉搏信号有明显的混沌趋势,这一结果和人体生理应激机制的一般规律相符.

3 结 语

对汽车振动噪声环境下脉搏信号的分布特点进行分析,能有效促进对人在噪声环境下的生理反应的研究,也能为汽车行业的发展提供理论支持,但仅从脉搏波形图很难得出不同振动噪声参数下的影响规律.

本文阐述了采用代替数据法计算脉搏信号有关特征参数的基本原理,分析并完成了对车辆平稳行驶及加速行驶两种不同工况下的实测脉搏信号,并通过3D谱阵图进行了对比分析.试验结果表明,平稳行驶及加速行驶工况下脉搏信号的特征参数数值有较大差异.

[1] 刘沛,庞宇,吴宝明.脉搏波形态特征与血压相关性的研究[J].生命科学仪器,2015,13(2):31-34.

[2] 徐可欣,王继寸,余辉.脉搏波时域特征与血压相关性的研究[J].中国医疗设备,2009(8):42-46.

[3] GOLDBERGER A L,WEST B J,RIGHNEY D R.Chaos and fractal in human physiology[J].Scientific American,1990,262(1):42-49.

[4] 刘磊,吴秋峰,张宏志.脉诊客观化研究综述[J].智能计算机与应用,2013,3(3):20-24.

[5] GOLDBERGER A.Fractal mechanisms in electrophysiology of the heart[J].IEEE Med Biol,1992:47-52.

[6] GOLDBERGER A L,Bhargara V,WEST B J,etal.On a mechanism of cardiac electrical stability:The fractal hypothesis[J].Biophys J.,1985(48):525-528.

[7] TSONIS A,ELSENER J.Nonlinear prediction as a way of distinguishing chaos from random fractal sequences[J].Nature,1992:217-223.

[8] GRASSBERGER P,Procaccia I[J].Measuring the strangeness of strange attractors.Phys. D,1983(9):189-199.

[9] THEILER J.Testing for nonlinearity in time series:the method of surrogate data[J].Phys. D,1992,58(1-4):77-94.

[10] CASDAGIL M.Nonlinear prediction of chaotic time series[J].Phys. D,1989,35(3):335-356.

(编辑 胡小萍)

Comparison of Nonlinear Characteristics of Human PulseWaves under Vibro-Noise Environments

YANG Feng, HAN Qingpeng

(SchoolofEnergyandMechanicalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

The chaos of pulse wave are identified by surrogate data method.Firstly,the main principle of chaotic identification is introduced,in which the median absolute error (MAE) of one-step prediction for pulse wave is set as the statistic.The algorithm is checked with a known chaotic system response and a colored noise signal.Then,some typical pulse waves under vibration and noise conditions are analyzed by means of surrogate data,and some characteristic parameters from this method are compared.

vibro-noise environment; pulse wave; surrogate data method; characteristic parameters

10.3969/j.issn.1006-4729.2016.05.017

2015-05-24

简介：杨峰(1984-),女,讲师,山东济宁人.主要研究方向为制造工艺、先进制造技术等.E-mail:yangfeng1310@126.com.

R318.04;TN911.7

A

1006-4729(2016)05-0495-04