基于关联维数的不同压力下液压管路振动信号的非线性分析
2016-12-15韩清鹏
韩清鹏, 朱 瑞, 梁 磊
(上海电力学院 能源与机械工程学院, 上海 200090)
基于关联维数的不同压力下液压管路振动信号的非线性分析
韩清鹏, 朱 瑞, 梁 磊
(上海电力学院 能源与机械工程学院, 上海 200090)
关联维数可定量分析不同压力状况下液压管路的工作状态.详细讨论了不同压力下液压管路系统的振动信号中关联维数的计算方法,并通过实验进行了分析.实验结果表明,通过偏相关积分算法计算得到的指数维数(关联维数近似值),能表征不同压力变化下的液压管路振动信号的变化,当压力变大时维数逐渐增大.
关联维数; 液压管路; 振动信号; 非线性
当液压系统管路中的介质突然换向、控制阀关闭或打开时,液体流速会发生急剧变化,产生液压冲击现象,造成较大的振动和噪声;系统中的柱塞泵引起的压力脉动和流量脉动也可以引起管路的振动;流体与管路之间产生的流固耦合现象,也会引起管路的振动,这些因素都影响系统的正常工作.[1]对不同压力下液压管路振动信号进行分析可以避免液压管路系统振动导致的严重事故,可改善液压管路系统的动态特性,提高可靠性,因此对这些振动故障的产生机制、故障特征,以及相应的设计处理方法和监测振动方法进行深入研究具有十分重要的意义.
不同压力下液压管路振动信号具有时变特征[2]和周期脉冲等特点.不同压力下的液压管路振动特征会发生变化.此时,最有效的分析方法是非线性动力学分析方法.不同压力下的液压管路振动信号是复杂的,具有非平稳的噪声和非线性特征,这些变化包括拟周期运动到完全无规则运动.[3]关联维数可以用来分析不同压力下液压管路振动信号和其非线性动力学特征.可以用偏相关积分算法计算指数维数,并由此推算出关联维数.[4-5]本文将详细讨论不同压力下液压管路系统的振动信号中关联维数的计算及其应用中的若干问题.
1 关联维数和关联积分的定义和计算方法
关联维数是分形维数的一种.所谓分形(Fractal)是指一类体形复杂的体系,其局部与整体具有相似性.[5]分形体的维数不一定是整数,它可以取连续变化的各种数值,称之为分形维数.分形与系统的混沌运动密切相关,是非线性科学研究的重要分支.分形维数的定义很多,主要包括容量维数或盒维数(Dc)、Hausdorff维数(Df)、相似维数(Ds)、信息维数(Di)、关联维数(Dr)等.
对一个时间序列进行关联维数估算时,原理清晰,过程简便,因而应用非常广泛.估算关联维数的基本原理如下.
按一定采样周期(dt)去测量得到的时间序列数据蕴涵着原系统的动力学运动的信息.根据相空间重构理论,利用测量数据构筑一个抽象空间,即嵌入空间(Embedded Space),即将测量数据嵌入在这样的空间内,然后再对这样的空间作分维分析.
测量数据记录为:x(n)={x(1),x(2),x(3),…,x(i),…,x(n)},其中,x(n)为idt时刻测量得到的数据.采用延时嵌入相空间重构的思想,步骤如下.
1.1 嵌入空间的构筑
对于单变量时间序列,x(i),i=1,2,3,…,N,进行嵌入空间构筑.设嵌入空间的维数(嵌入维数)为p,构筑如下向量代表该系统在该时刻(idt)的状态:
(1)
式中:g——时延常数(嵌入间隔).
所有Di组成的序列为整个测量数据在嵌入空间内的所有点向量组成的序列,即:
(2)
在这里g不可太大也不可太小.
1.2 关联积分的计算
为了计算由时间序列包含的动力学信息,引入关联积分的概念.在嵌入空间构筑完成后,任选一个参考点Di,计算其余各点到它的距离,即:
(3)
对事先设定的一个距离值r,检查rij与设定值r的对比,如果rij (4) 式中:H——阶跃函数(Heaviside函数). (5) 1.3 关联维数的计算 讨论关联积分(相关积分)C(r)与r的关系.根据C(r)的定义,可以定性地看出,C(r)随着r的增加而增加,但C(r)随r增加的趋势与运动状态有关.如果系统作周期运动,随着r的增加,C(r)将不变或者变化很慢;而系统作混沌运动时,C(r)将随r的增加而单调增加.与容量维数的计算方法基本相同,定义如下关联维数,即一维曲线散落在尺度r内的点数正比于r的一次方,二维平面上散落在尺度r内的点数正比于r2,三维体积内散落在尺度r内的点数正比于r3.因此,对于关联积分与关联维数的对应情况,应有: (6) 式中:A——比例常数. 对式(6)取对数,有: logC(r)=Drlogr+logA (7) 取不同的r值对式(7)作图,将得到一直线(logC(r)-logr曲线),直线部分的斜率即为所求的维数. 1.4 几个重要参数的讨论 (1) 嵌入维数p在实际计算时,嵌入空间的维数p十分关键.根据有关研究,选择嵌入空间的维数p=2Dr+1进行重构才合理.一般可以从小到大取数个p值,画出Dr-p曲线.可以发现开始时Dr会随p的增加而增加,以后会逐渐变慢以至恒定,这时就可以确定Dr. (2) 时延常数g时延常数g太小,重构的吸引子在坐标中处于主对角线位置,表明x(t)与x(t+τ)(τ=gdt)太近,不可以充当独立的坐标.理论上g应取足够大,以保证相空间中各变量不相关.但g太大时,要求数据序列太长,在很多情况下并不合适.这里,采用x(n)的自相关函数降到初始值的1/e倍的方法确定g值. (3) 数据长度N由于实验中的信号将不可避免地含有噪声,同时数据长度不可能是无限长,因此在实际应用中,数据长度和噪声干扰是影响关联维数计算结果的重要因素.考虑数据长度N对Dr的计算影响时,同时还应考虑与采样频率的关系,根据有关资料,在计算含噪声吸引子关联维时,采样频率应是信号平均周期频率的50~200倍.Kantz给出了Nmin=10(Dr+2)/2,以估计最小样本长度.采样频率对Dr的影响一般很小. (4) 噪声影响 实验或现场采集到的信号都不可避免地含有噪声干扰.当信噪比高于50时,关联积分有足够的收敛区间,可以可靠地估计信号的关联维数. 本文通过利用上述方法分析不同压力情况下液压管路的振动特征,计算出不同压力下液压管路振动信号的指数维数. 2.1 实验设计 液压管路振动实验系统如图1所示.油系统主要采用齿轮泵或柱塞泵提供动力,其工作方式可以在地面实际液压系统中复现,以定性分析齿轮泵或柱塞泵的液压系统中管路的振动状态. 本次实验主要测试柱塞泵出口处的一段管路,其中包含一段弯管,一个单向阀,一个高压胶管,具有比较典型的特征.选取了5个测试点,对柱塞泵出口处测试点1进行分析,其中当压力变化分别达到10 MPa,19 MPa时,恒压变量泵动作.使用IOTECH650记录数据,采样频率为 1 kHz.图2为不同压力下液压管路振动信号频域图. 图1 液压管路振动实验系统 2.2 不同压力下液压管路振动信号关联维数的计算与比较 对不同压力作用下的液压管路振动信号进行关联维数估算时,首先采用延时坐标法对其进行相空间重构,其中采用互信息法确定其延迟时间,即利用信号自身的互信息函数确定用于时间滞后重构合适的滞后时间.图3是两组不同压力作用下的液压管路振动信号的最小延迟时间,这里采用x(n)的自相关函数降到初始值的1/e倍的方法确定g值,分别为11和8,对应图3各曲线中的第一个极小值点. 根据关联积分的对数lnC(r)与度量尺度对数ln(r)之间存在的线性区域,利用最小二乘法估算出这个线段的斜率,所得结果即为不同压力作用下的液压管路振动信号时间序列的关联维数.图4为上述两组不同压力下的液压管路振动信号的lnC(r)-ln(r)曲线,估算得到的关联维数分别为2.957 3,3.755 9. 图2 不同压力下液压管路振动信号频域分析 图3 根据互信息法确定最小延迟时间 由此可知,关联维数可以用来量化振动信号的非线性特征.随着压力越来越大,复杂度也越来越大,关联维数代表了系统的复杂度. 图4 关联积分与度量尺度曲线 关联维数反映了压力突变下液压管路振动信号中的频率成分.随着压力的逐步升高,其关联维数的变化也由低到高逐渐增大,因此关联维数值能够很好地反映压力突变下液压管路振动信号的频率高低. [1] LI B,CHOW M Y,TIPSUWAN Y,etal.Neural-network based motor rolling bearing fault diagnosis[J].IEEE Transactions on Industrial Electronics,2000,47(1):1 060-1 069. [2] SAMUEL P D,PINES D J.A review of vibration-based techniques for helicopter transmission diagnostics[J].Journal of Sound and Vibration,2005,282(1):475-508.[3] HIVELY L M,PROTOPOPESCU V A.Machine failure forewarning via phase-space dissimilarity measures[J].Chaos,2004,14(2):408-419. [4] 谢全民,龙源,钟明寿,等.小波包与分形组合技术在爆破振动信号分析中的应用研究[J].振动与冲击,2011,30(1):11-15. [5] 陈新,黄洪钟,黄文培.分形理论及其在机械工程中的应用[J].机械科学与技术,2000,19(5):692-695. (编辑 桂金星) Nonlinear Analysis of Hydraulic Pipe Vibrating Signals Under Different Pressures Based on Correlation Dimensions HAN Qingpeng, ZHU Rui, LIANG Lei (SchoolofEnergyandMechanicalEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China) The correlation dimensions can be applied to quantitatively analyze the hydraulic pipe vibration signal under different pressures.The correlation dimensions of the vibration signals of hydraulic pipe of different pressures,the fractal dimension changes of different frequency components of hydraulic pipe vibration signal under different pressures are discussed in detail.The correlation dimensions change with the frequency of hydraulic pipe vibration signals under different pressure is analyzed.It is showed that the correlation dimensions are an important parameter. correlation dimensions; hydraulic pipe; vibration signals; nonlinear 10.3969/j.issn.1006-4729.2016.05.011 2015-03-23 简介:韩清鹏(1973-),男,博士,副教授,山东济宁人.主要研究方向为振动与非线性分析.E-mail:han1011@163.com. TH137 A 1006-4729(2016)05-0463-04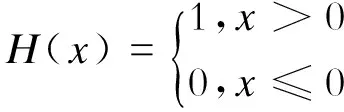
2 不同压力条件下液压管路振动信号分析

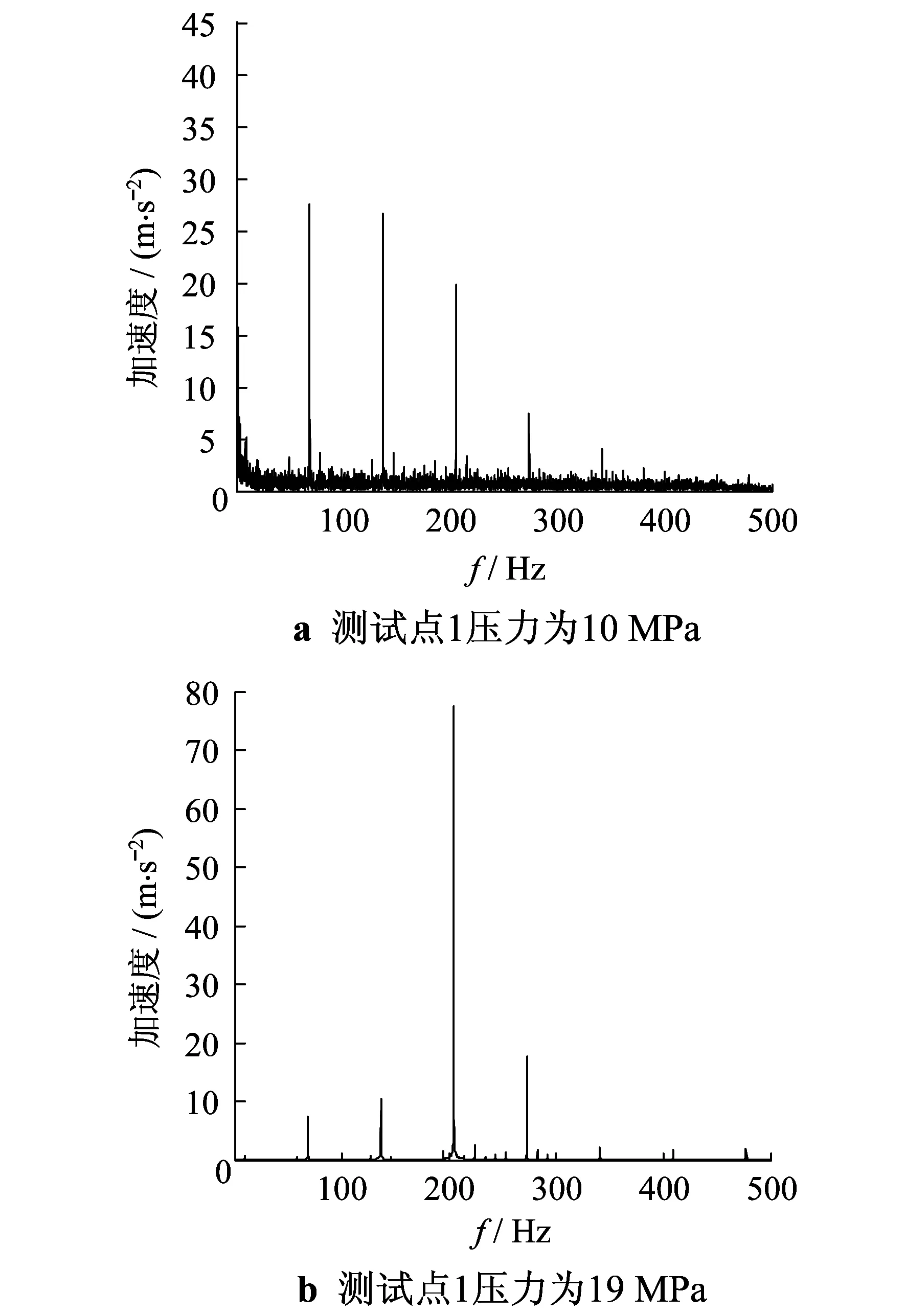
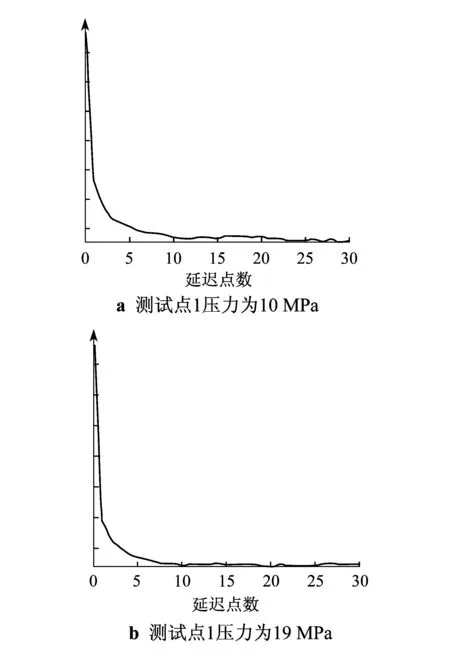
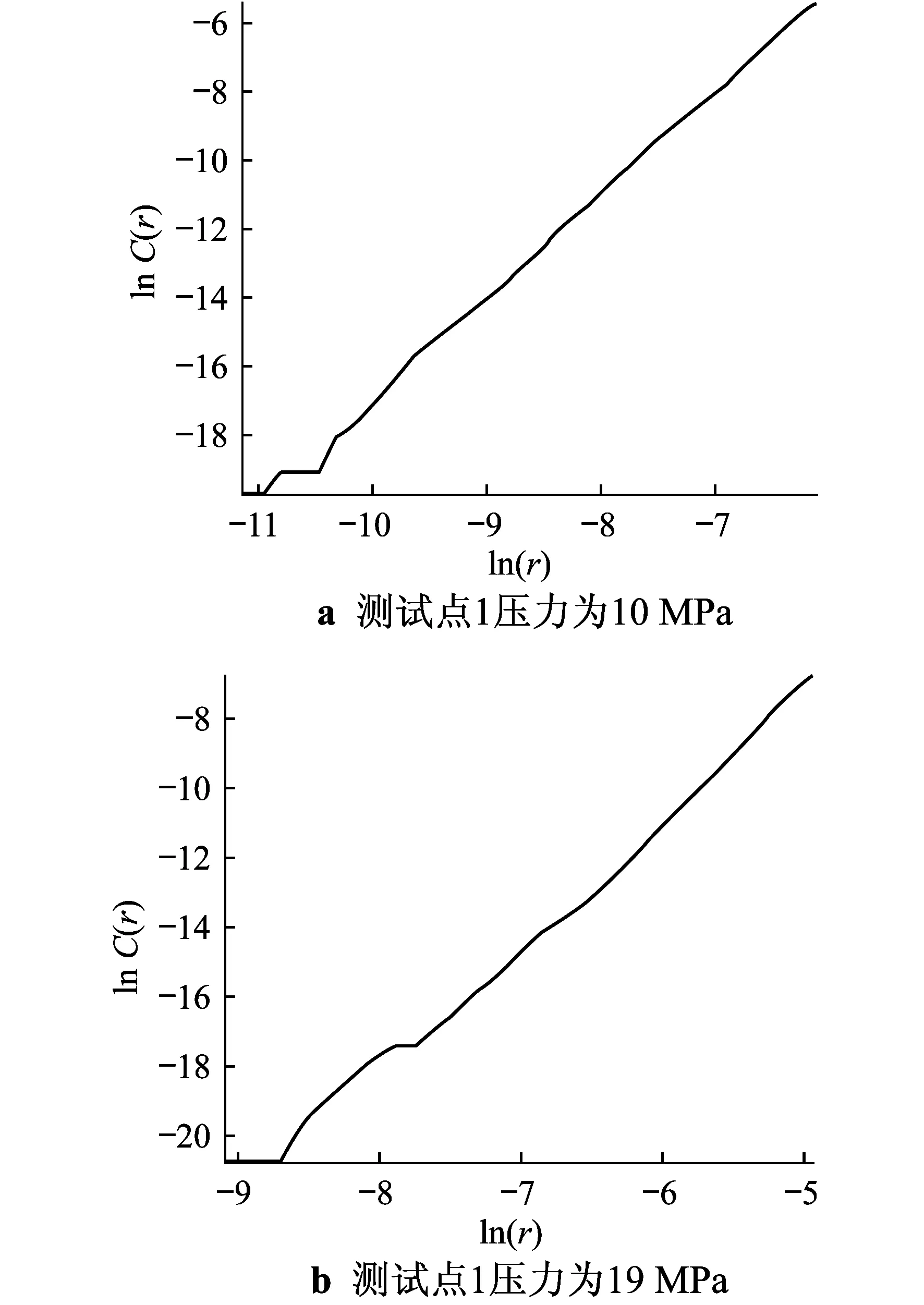
3 结 语
