无序三维点云重建技术研究

2016-12-15胡友健

测绘通报 2016年9期

关键词：三角网无序栅格

龚珍，胡友健，董恒，黎华

(1. 武汉理工大学资源与环境工程学院，湖北武汉 430079； 2. 中国地质大学，湖北武汉 430079)

无序三维点云重建技术研究

龚珍1,2，胡友健2，董恒1，黎华1

(1. 武汉理工大学资源与环境工程学院，湖北武汉 430079； 2. 中国地质大学，湖北武汉 430079)

如何对海量三维点云数据进行快速三维重建是三维场景重现中关键的问题。本文从项目出发，对采集的无序点云提出根据内容进行重建，对非关键区域进行数据压缩，将压缩后的数据与关键区域的数据放在一起进行三维重建。试验结果表明，该方法能完整地呈现三维场景中的地物，同时也能减少三维场景重建的时间，可以为类似的三维重建提供一定的参考依据。

三维场景重建;无序点云;数据压缩;数据分类

三维激光测量技术是一种快速、准确获取真实地物空间信息的技术。采用三维激光扫描仪对被测量地物进行扫描，操作简单且精度高。由于获取的三维点云数据量庞大、散乱，如何组织这些点云数据，使得其通过计算机虚拟地呈现出来，成为空间信息处理、计算机图形学、计算机视觉等领域研究的热点。

点云按照排列方式的不同可以分为有序点云和无序点云[1]。有序点云的点与点的拓扑结构完整，相邻点之间存在连续关系，领域操作高效。无序点云由于点与点之间缺乏拓扑关系，因此常采用八叉树、空间单元格、kd-tree数对其进行管理。本文主要研究无序点云的三维重建，为点云快速重建提供基础。

一、点云重建国内外研究现状

根据重建曲面和数据点云之间的关系可将曲面重建分为两大类：插值法和逼近法。前者得到的曲面重建完全通过原始数据点，而后者则是通过分片线性曲面或其他形式的曲面类逼近原始数据点，从而得到的是重建曲面是原始点集的一个逼近。

插值法常用的算法有Delaunay三角网重构法[2-3]，该方法将三维点云数据的空间坐标投影到二维平面上，然后针对二维投影平面进行缺失补充，将投影的二维平面三角网格化，再利用反向映射的思想得到三维网格重建模型，最后完成点云数据的重建。由于该算法需要构造三角网格，因此具有很好的网络拓扑结构，然而在两次投影转化计算过程中存在维数的压缩，这样很可能导致点云数据空间深度信息的改变或丢失，这种两次转化投影的方式很难处理封闭或点云模型表面被遮挡的情况。后来在点云重建方面也出现了基于Delaunay空间区域增长方法的改进算法，即选取一个三角面片作为种子面片，在保证拓扑结构正确和几何结构正确的前提下，对种子面片进行扩张，最后形成完整三角网格曲面，改进算法有最小内角最大等优秀特性，但对于点云，当数据中的三维点进行三角网格剖分的时间复杂度较大，如果点云数据达到千百万数量级，Delaunay三角网格剖分算法的点云数据重建时间过长，因此此方法并不适合大规模点云数据的重建操作[4]。

逼近法常用的算法有泊松重建、MC重建、EarChipping重建。即通过最优化的插值方法，对点云数据进行处理，进而获得点云模型的近似曲面。

二、三维点云快速重建算法

为了解决现有的Delaunay三角网重建算法中存在的算法效率低下的问题，本文提出并采用根据内容进行压缩的快速Delaunay三角网重建方法。首先根据研究内容对非关键区域采用包围盒压缩算法进行点云数据压缩，然后利用贪婪投影三角化算法将压缩区域的点云和非压缩区域的点云进行三维点云重建。

1. 基于包围盒的点云数据压缩

根据点云中点的分布特点，可将点云分为有序点云和散乱点云。对于有序点云的数据压缩，常用的采样方法有均匀采样法、倍率缩减法、栅格法、等量缩减法、最小包围盒区域法、等分密度法等。散乱点云数据压缩中，常用的方法有随机采样法、最短距离法、包围盒法、均匀格网法、三角网格法、曲率采样法等[5-10]。

目前，针对点云的压缩大致可以分为3类：基于概率的数据精简(随机采样法)、基于格网的数据精简法(包围盒法、均匀格网法等)和基于曲率的数据精简法(最短距离法、曲率采样法)[5]。

包围盒重心法是点云处理中较为常见的方法，其核心思想是用包围盒中点云的重心来代替点云中的点实现数据精简。其实现方法为：首先采用一个最小外包长方体来约束点云，然后将长方体根据一定的数量或大小分割成若干个小立方体包围盒，最后选取小包围盒中离点集的重心点最近的点作为特征点，即每个包围盒中最多只保留一个数据点。算法流程如图1所示。

图1

2. 试验结果

(1) 数据处理

由于现有的数据格式(*.ply,*.stl,*.obj,*.x3d)格式不支持PCL库，PCD格式能支持PCL数据库引进的n维点类型机制处理中的某些扩展，因此，需要将采集到的数据按照PCD格式进行转化，PCD格式如图2所示。其中，version表示PCD文件版本，fields表示一个点可以有的每一个维度和字段的名字，size表示每一个维度的大小，type表示每一个维度的类型，count表示每一个维度包含的元素数目，width表示点云数据集的宽度，height表示点云数据集的高度，viewpoint表示数据集中点云获取的视点，data表示存储的点云的数据类型。

图2

(2) 数据压缩

PCL提供了两种点云数据管理方式，一种是kd-tree数据结构，一种是octree数据结构，也称八叉树。其中，kd-tree树用来对点云数据进行检索，octree树在PCL中用于点云数据压缩。因此，本文采用八叉树对点云数据进行管理和压缩。

对采集到的点云数采用八叉树进行数据管理，构造点云数据的最小空间包围盒，并把它作为数据点云拓扑关系的根模型；再将外界立方体分割成大小系统的8个子栅格，每个子栅格均视为根节点的子节点；如此递归分割，直到最小子栅格的边长等于给定的点距，将点云空间划分成为2的幂次方个子栅格。

由于PCL库中提供了十几个基于八叉树(octree)的点云高效管理、检索、空间处理算法库，因此，本文用采集到的数据点将数据分为变形区和非变形区，将非变形区的数据采用八叉树进行组织，在此基础上采用基于最小包围盒的方式对数据进行压缩，压缩前后的效果如图3、图4所示。图3中数据的压缩比为0.25%，数据点为2928；图4中数据的压缩比为4.5%，数据点为52 374。

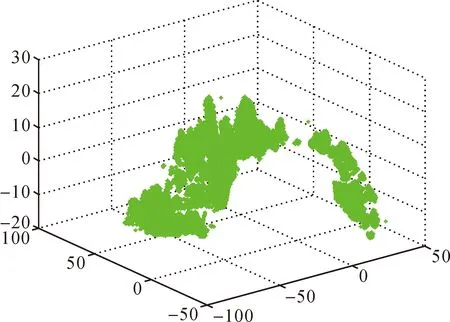
图4

三、场景重建

为了减少海量点云数据的三角网生成时间，本文将非变形区域的数据和变形区域的数据融合在一起进行三角网重建，贪婪三角网算法原理处理一系列可以使网格“生长扩大”的点，延伸这些点直到所有符合几何正确性和拓扑性的点都参与构网。其具体做法是将点云投影到某一局部二维坐标平面内，再在坐标平面内进行平面内的三角化，根据平面内的拓扑连接关系获得一个三角网格模型。基于上述思想，本文将压缩后的非变形区域点云和变形区域点云放在一起进行三角网重建，其中变形区域观测点为12 470 691个。

在图5中的程序参数设置如下：

连接点之间的最大距离设置为300，gp3.setSearchRadius(300);

样本点搜索其邻近点的最远距离为40，gp3.serMu(40);

三角化后得到的三角形最小角度为10°，gp3.setMinimumAngle(10);

三角化后得到的三角形最大角度为120°，gp3.setMaxmumAngle(120);

当某一待选点的法线方向偏离某一样本点超过45°时，该点不连接到样本点上，gp3.setMaximumSurfaceAngle(45);

样本可搜索的领域个数为100个，gp3.setMaximumNearestneighbors(100)。

效果如图5所示。

在图6中的程序参数设置如下：

连接点之间的最大距离设置为300，gp3.setSearchRadius(300);

样本点搜索其邻近点的最远距离为60，gp3.serMu(60);

图5

三角化后得到的三角形最小角度为10°，gp3.setMinimumAngle(10);

三角化后得到的三角形最大角度为120°，gp3.setMaxmumAngle(120);

当某一待选点的法线方向偏离某一样本点超过45°时，该点不连接到样本点上，gp3.setMaximumSurfaceAngle(45);

样本可搜索的领域个数为100个，gp3.setMaximumNearestneighbors(100)。

效果如图6所示。

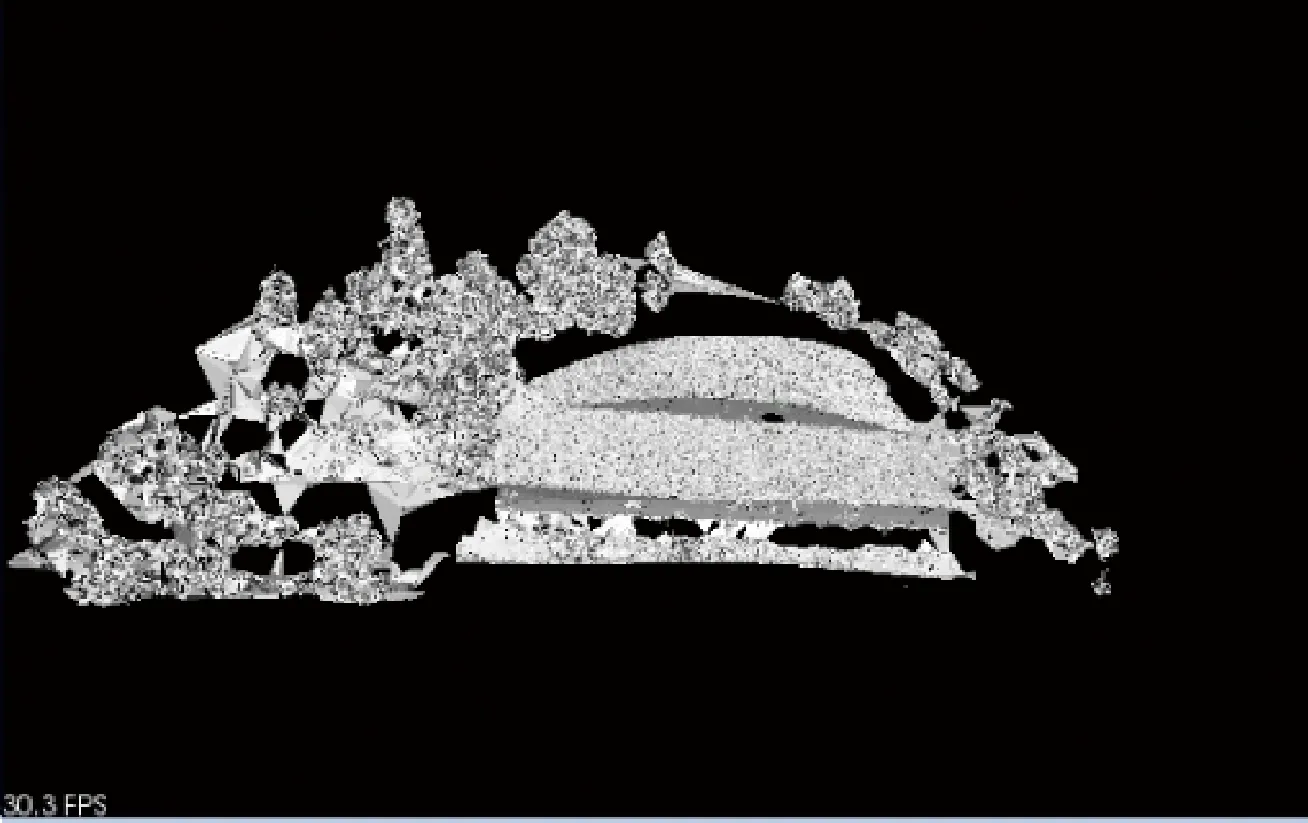
图6

四、结束语

由于三维激光点云能够便捷、高效地获取数据，因此具有广阔的应用前景[11-12]。由于在扫描过程中，有些区域反射率太低，使得该区域的数据无法获取，导致在三角网重建过程中出现了空洞。本文主要是根据项目需要对三维点云数据的压缩方式进行了研究，利用PCD格式支持数据扩展的优势，提出根据内容来对点云进行压缩，采用贪婪三角网算法对压缩之后的无向点云进行重建。试验结果证明该方法可行，这为三维点云的重建提供了新的思路。

[1] 樊宇，王宇楠.三维激光扫描点云数据预处理技术研究[J].科技创新导报，2011(32):27-28.

[2] 吕琼琼.激光雷达点云数据的三维建模技术[D].北京：北京交通大学, 2009.

[3] 梁群仙，许宏丽.一种基于点云数据的快速曲面重构方法[J].计算机工程学报(图形图像处理)，2013,39(2):238-240.

[4] 梁锡坤.B 样条类曲线曲面理论及其应用研究[D].合肥：合肥工业大学,2003.

[5] 喜文飞.激光点云数据压缩的精简研究[D].昆明:昆明理工大学,2012.

[6] 赵俭辉，龙成江，丁乙华，等.一种基于立方体小栅格的K邻域快速搜索算法[J].武汉大学学报(信息科学版),2009(5):615-618.

[7] 刘越华，廖文和，刘浩.逆向工程中散乱点云的K邻域搜索算法研究[J].机械设计与制造,2012(3):256-258.

[8] 孟娜.基于激光扫描点云的数据处理技术研究[D].济南：山东大学,2011.

[9] 黄文明，肖朝霞，温佩芝，等.保留边界的点云简化方法[J].计算机应用,2010(2):348-350.

[10] 杨楠，校江超，王明海.利用点云数据的法矢及曲率估算[J].现代制造工程,2010(7):35-37.

[11] 卢小平，王宇飞，杜耀刚，等.利用点云构建隧道断面的形变监测方法[J].测绘通报，2016(1):80-83.

[12] 李珵, 卢小平, 朱宁宁, 等.基于激光点云的隧道断面连续提取与形变分析方法[J].测绘学报，2015,44(9):1056-1062.