石英挠性加速度计标度因数受气压影响分析

黄丽娟，吕江涛，郑永强

（中国航天科工集团第九总体设计部，武汉430040）

石英挠性加速度计标度因数受气压影响分析

黄丽娟，吕江涛，郑永强

（中国航天科工集团第九总体设计部，武汉430040）

石英挠性加速度计是惯导产品的核心器件之一，主要敏感载体运动中的加速度，为系统提供位置信息。加速度计具有力学敏感特性，其测量精度易受环境因素变化的影响。针对加速度计在不同地域测试时标度因数发生较大变化的问题，分离了加速度计异地测试过程中的时漂、温变、形变等多个环境因子后，提出了造成加速度计异地标度因数改变的主要原因是环境气压发生了较大变化。根据石英挠性加速度计的基本原理，结合加速度计检测质量摆的具体受力情况，对气压变化造成加速度计标度因数改变的机理进行了详细分析，给出了标度因数随气压变化的相对变化理论计算公式，经过验证试验，实测情况与理论分析结果一致，可以为石英挠性加速度计的优化改进提供参考依据，具有一定的工程应用价值。

加速度计；标度因数；气压影响；理论分析；试验验证

0 引言

惯导设备因具有全自主、可靠性高、抗干扰能力强、动态特性好等特点，在火箭系统、空间运载以及地面导航中得到大量应用［1］。因惯导设备的精度直接影响火箭系统的制导精度，在实际应用中，用户方对惯性产品的使用性能提出了与精度相关的两大需求［2］。一是性能保持期长，比如从3个月延长到6个月，再到1年，甚至提出了免标定的需求，减少维护产品的人力和物力，力求使用方便、简单、快捷，提高整个系统的待机能力［5］；二是环境适应能力强，能够适应不同地域、不同气候和不同使用环境的需求，特别是在进行长期大范围跨地域的机动后，能够保持产品的精度，提高火箭系统的反应能力和作战效能［3］。

惯导设备主要由陀螺和加速度计两大核心部件组成，分别敏感载体运动中的角速度和加速度。随着国内光学技术的发展进步，光学陀螺已经得到大量应用和装备，精度和可靠性得到充分验证；而加速度计暂未有新的技术突破，仍以石英加速度计为主，较易受环境的影响是整体性能提升的难点。本文针对加速度计异地使用标度因数变化较大的现象进行了分析，在排除时间、温度、形变等因素的影响后，提出主要是受气压变化的影响。传统的整机密封措施受制于国内工艺技术和检测手段的限制，难以有效检测和消除缓慢漏气的现象，需要进行改进和完善［4］。

1 现象描述

近年来，惯导产品经常随系统执行高原任务。在发射阵地测试时，有一定比例的惯组加速度标度因数稳定性超差。例如，在某次任务中，惯导产品在某总装生产地标定测试后，随系统转场到高原某地进行发射试验，产品到达目的地并放置1天后进行标定测试，结果有一部分惯导产品的加速度标度因数发生较大变化，具体结果如表1所示，约占产品总数量的五分之一；其他通道变化量均在1．0×10-5以内。

从表1中可以看出，10个加速度计通道标度因数的变化方向均为正向（增大），RMS值为1．18× 10-4。后续对上述惯组进行二次标定，在高原的两次结果变化不大（均在1．0×10-5以内）。

表1　某次任务加速度计标度因数变化情况Table 1 The scale factors of some accelerometers

2 问题初步分析

针对上述问题，对标度因数发生变化的主要原因进行了分析，主要有如下几个方面［5］：

1）加速度计、I／F变换电路的器件参数随时间发生漂移；

2）运输过程中的力学振动导致加速度计参数发生改变；

3）惯导内部温度环境改变引起加速度计和I／F变换电路参数发生改变；

4）其他外界环境引起的结果。

2.1 参数随时间发生的漂移

在惯导产品中，加速度计、I／F变换电路的某些器件均会随时间发生缓慢的漂移。而上述测试时间间隔不到10天，在短时间内发生的综合漂移一般在1．0×10-5以内。因此基本可以排除参数漂移1．0×10-4的情况。

2.2 运输导致的参数改变

惯导产品经历振动、运输等力学环境后，对挠性加速度计的质量摆片可能产生一定的应力，这种应力会给质量摆片造成一定的形变，从而影响到加速度计的标度因数值。

在当次试验任务中，惯导产品放置在有良好减震措施的包装箱中进行运输，产生的应力得到缓冲；产品到达目的地后，放置了1天以上再进行测试，应力释放较充分；另外，若应力释放不充分，也会对加速度计零位产生影响，但上述各通道对应的零位变化均在1．0×10-5g以内。因此，可以排除力学环境带来的参数改变。

2.3 内部温度环境改变引起的参数改变

这批惯导产品内部均采取了两级温控，控温精度在0．5℃／4h以内；惯导产品的标定测试间温度控制在20℃±5℃，由外部环境产生的温差很小。另外，惯导内部温度改变同时会影响加速度计零位、陀螺标度因数等参数，上述产品的加速度计零位、陀螺标度因数变化均很小。因此，可以排除温度环境带来的参数改变。

2.4 其他外界环境引起的结果

在其他环境因素中，惯导产品从内地转场到高原某地，海拔高度有明显的改变，这种改变对加速度计测量带来的影响主要表现在重力加速度和大气压强。

对于重力加速度，惯组标定测试间建造时都进行了重力加速度的精确测量，并定期进行复验；在惯组标定测试结果计算时，已考虑了不同地点的重力加速度差异，因此不会因重力加速度的改变带来误差。

对于大气压强，因对石英挠性加速度计有密封要求，因此对气压可能带来的改变没有给予考虑。

下面详细分析因海拔高度不同引起的大气压强改变会给加速度计标度因数带来的影响。

3 海拔高度影响分析

3.1 石英挠性加速度计的组成及原理

石英挠性加速度计由表头和伺服电路两部分组成。表头主要由整体石英挠性摆组件、差动电容传感器、力矩器、壳体等部分组成。其中，整体石英挠性摆组件由中电盘、安装环、连接中心盘、安装环的2个挠性平桥及固定在中心盘上的2个铝质骨架的力矩器动圈组成。石英摆片的镀金区形成差动电容传感器的2个动极板，力矩器由2个铁磁组合和2个顺向连接的力矩器动圈组成。表头的内部结构示意图如图1所示［9］。

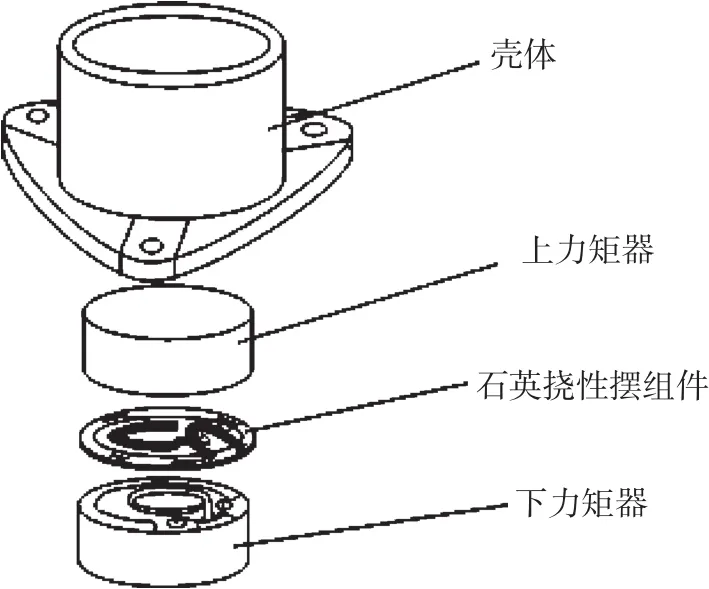
图1　表头内部结构示意图Fig.1 The interior structure of accelerometer

石英挠性加速度计的工作原理为［8］：石英挠性加速度计安装在要检测的载体上，当载体在加速度计输入轴方向上相对惯性空间以加速度a运动时，加速度计检测质量摆将产生惯性力矩Mg=mla，惯性力矩使检测质量摆沿挠性轴产生角位移，该角位移使差动电容传感器产生电容差值，经伺服电路变换成与加速度a成比例的电流信号I，该电流使力矩器产生一电磁反馈力矩Mt=Kt·I。当反馈力矩与惯性力矩相平衡时，即有：

其中，m为检测质量的质量；l为检测质量的质心到挠性轴的距离；Kt为力矩器的标度因数（kg·m2／s2·A）。

式（1）中，m、l、Kt都是常量，因此测量出电流I即可得到沿输入轴方向的加速度a。加速度计的原理框图如图2所示。

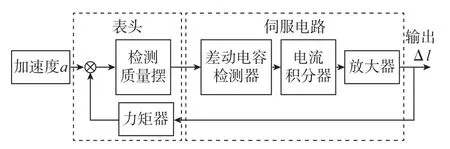
图2　加速度计原理示意图Fig.2 Principle of accelerometer

3.2 加速度标度因数值的力学原理分析

根据石英挠性加速度计的测试原理及牛顿力学原理，加速度计标度因数测试时，是将检测质量m置于水平状态下，认为此时检测质量m受到2个力：向下的重力mg，向上的反馈力Ft，且2个力产生的力矩平衡［6］。

则由上述原理可得，测试点重力加速度g0对应的反馈力矩电流值I0为：

式（2）变为：

式（3）中，因m、l、Kt都是常量，I0与测试点的重力加速度g0呈正比例关系。I0可以通过地面测试得到，因此将式（3）中的（I0/g0）定义为重力加速度g0对应的测试标度因数值［8］。

而实际上，上述推理忽略了环境中空气对检测质量m产生的浮力。下面讨论空气浮力在加速度计实际测量中带来的影响。

当考虑空气浮力情况时，检测质量m受到3个力：向下的重力mg、向上的反馈力Ft、空气浮力Ff，有：

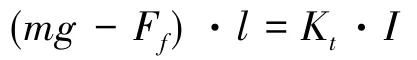
检测质量m置于水平状态时，为：

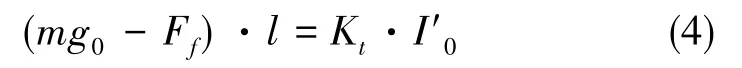
设检测质量m的密度为ρm、体积为V，测试点的空气密度为ρf，则有：

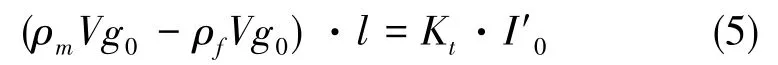
式（5）化为：

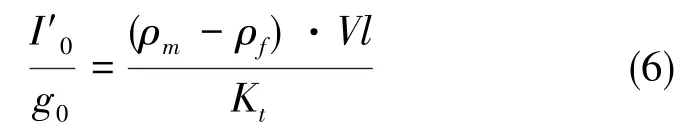
式（6）即为考虑空气浮力的标度因数值。

又因空气密度ρf与大气压强有关，有如下关系：

式（7）中，P为实际大气压强；P0为标准大气压强；T为实际温度的绝对温度；T0为0℃时的绝对温度。

而实际大气压强P与海拔高度有关，有如下关系：

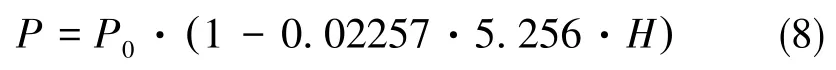
式（8）中，H为海拔高度。

式（7）、式（8）代入式（9），得到考虑空气浮力影响的标度因数值为：

从式（9）可以看出，空气产生的浮力对加速度计标度因数测量值的影响最终也就是海拔高度H带来的影响。当实际温度T为恒定值时，环境对标度因数的主要影响因素也就是海拔高度H。

3.3 海拔高度的影响分析

假定惯组进行了甲、乙两地的标定测试，其中甲、乙两地空气密度分别为ρf甲、ρf乙，两地重力加速度都为g0甲、g0乙。根据式（6），分别得到甲、乙两地的重力加速度标度因数值I0甲、I0乙：

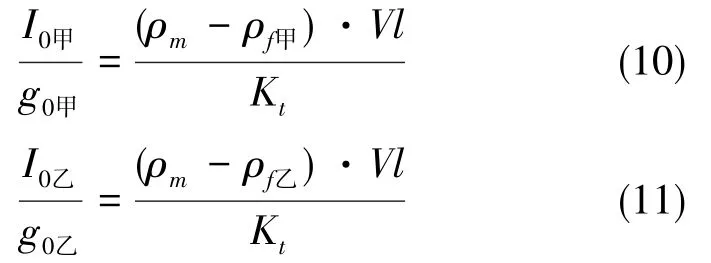
因空气浮力引起的两地标度因数相对差δ为：

假定两地测试时加速度计环境温度T相同，甲、乙两地海拔高度分别为H甲、H乙，将式（7）、式（8）代入式（12），得：

从式（13）可以看出，当加速度计环境温度为恒定值时，加速度计标度因数相对变化与两地的海拔高度差（H乙-H甲）成正比，且变化方向一致。高度差越大，标度因数相对变化越大。

4 分析结果试验验证

4.1 气压变化前后标度因数验证测试

为了验证上述分析结论，取部分加速度计进行验证测试。验证条件为：

1）加速度计前后两次测试的环境大气压强相差△P=0．4P0；

2）测试环境温度均为恒定的58℃。

（1）理论分析结果

根据验证条件，代入式（12）、式（7），可得到标度因数变化的理论分析结果δ理为：

（2）实际验证结果

验证过程：

1）取生产中有缓慢漏气现象的石英挠性加速度计30只，在加速度计测试间自然放置，每隔3天左右进行1次标度因数测试，测试环境温度基本恒定在58℃±0．5℃以内，共测试3次。

2）取其中28只标度因数稳定性1σ＜4．0×10-6的5只加速度计进行本次验证试验。将这28只加速度计放置到低气压箱中，将箱中气压降到标准大气压的0．6倍（测试环境大气压强P≈0．994P0，按P0计），保持箱内气压3天。

3）将28只加速度计取出立即进行测试，得到降低气压后的标度因数值。

较之于降低气压前的测试结果，有5只加速度计标度因数相对变化大于1．0×10-4，其余23只加速度计标度因数相对变化小于1．0×10-5。相对变化较大的5只加速度计的测试数据如表2所示。

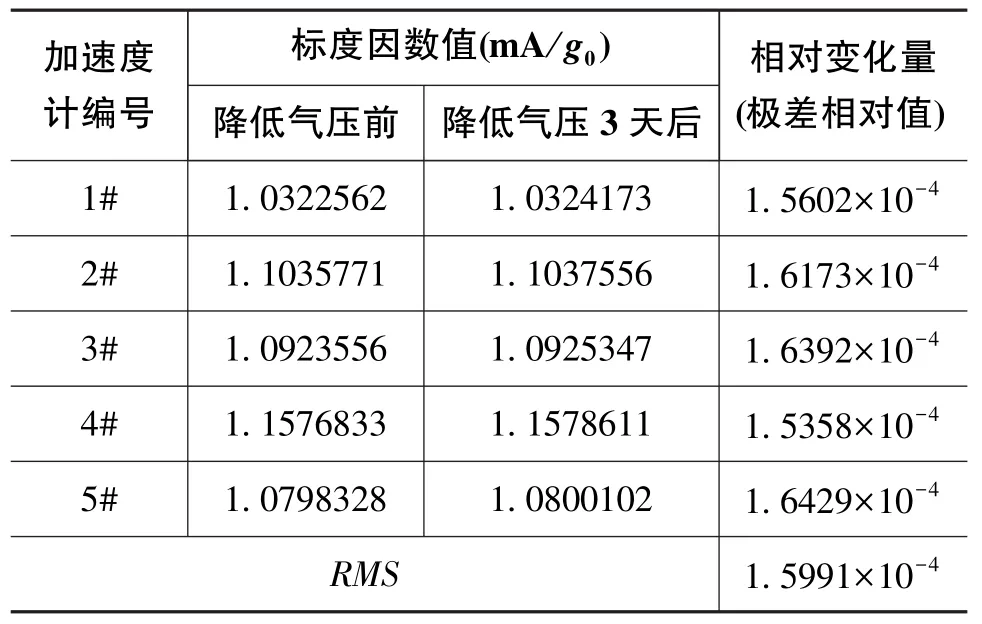
表2　5只加速度计气压变化前后标度因数值Table 2 The scale factors of 5 accelerometers before＆after affected by air pressure

从表2的测试结果可以看出，降低气压后与降低气压前的标度因数值相对变化量与理论计算结果1．6097×10-4非常接近（差值均不大于1．0×10-5）。

为了排除加速度计自身参数漂移，将5只加速度计在原测试间自然放置3天后，再次进行标度因数测试，与降低气压前比较，标度因数变化均小于1．0×10-5（极差相对值）。

由此验证了上述分析结果的正确性。

4.2 本文第1章数据结果的理论分析

对本文第1章中的测试结果进行验证性计算。假定内地惯组测试间为甲地、高原发射场惯组测试间为乙地，各地理参数如表3所示。

表3　两地测试环境参数Table 3 The environment parameters of the two places

将表3中的参数代入式（13），得到由空气浮力（海拔高度）改变引起的标度因数相对误差为：

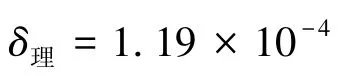
扣除因浮力引起的标度因数相对误差1．20×10-4后，惯组在高原测试时加速度计标度因数实际漂移不超过1．0×10-5，与上述产品在高原的两次测试数据较接近，也符合该状态石英挠性加速度计的标度因数稳定性能。

5 结论

本文通过某批惯导设备加速度计标度因数异地标定结果超差问题，对两地测试环境差异进行了分析，发现引起石英挠性加速度计标度因数超差的主要原因是部分加速度计密封后存在缓慢漏气现象，在异地放置一段时间后，内部气压按新的环境逐渐稳定到一个新的气压状态，导致加速度计摆片受力发生变化，从而引起测量标度因数变化。通过对部分试验器件的验证，证明了本文分析结果的正确性。

本文的分析结论可以给石英挠性加速度计的生产、应用者提供参考，也可以为加速度计的改进设计提供依据，有较高的工程应用价值。

［1］Lv B J，Wang P F，Wang D B，et al．A high⁃performance closed⁃loop fourth⁃order sigma⁃delta micro⁃machined ac⁃celerometer［J］．Key Engineering Materials，2012，503：134⁃138．

［2］Yang J，Wu W Q，Wu Y X，et al．An iterative calibration method for nonlinear coefficients of marine triaxial acceler⁃ometers［J］．Journal of Central South University，2013，20（11）：3103⁃3115．

［3］刘建波，魏宗康．石英加速度计误差系数显著性分析［J］．中国惯性技术学报，2011，19（5）：615⁃620．LIU Jian⁃bo，WEI Zong⁃kang．Significance analysis of QFPA's error model's coefficients［J］．Journal of Chinese Inertial Technology，2011，19（5）：615⁃620．

［4］张鹏飞，龙兴武．石英挠性加速度计误差补偿模型的研究［J］．传感技术学报，2006，19（4）：1100⁃1102．ZHANG Peng⁃fei，LONG Xing⁃wu．Research on compen⁃sating error model of quartzose flexible sccelerometer［J］．Chinese Journal of Sensors and Actuators，2006，19（4）：1100⁃1102．

［5］王世明，任顺清．精密离心机误差对石英加速度计误差标定精度分析［J］．宇航学报，2012，33（4）：520⁃526．WANG Shi⁃ming，REN Shun⁃qing．Relationship between calibration accuracy of error model coefficients of acceler⁃ometer and errors of precision centrifuge［J］．Journal of Astronautics，2012，33（4）：520⁃526．

［6］高雅彪，毛伟玲，李醒飞．石英挠性摆式加速度计闭环检测电路设计［J］．电子技术应用，2012，38（2）：70⁃76．GAO Ya⁃biao，MAO Wei⁃ling，LI Xing⁃fei．A closed⁃loop detection circuit for quartz flexure accelerometer［J］．Ap⁃plication of Electronic Technique，2012，38（2）：70⁃76．

［7］李安，张云电．石英挠性加速度计摆片组件的应力分析［J］．机电工程，2010，27（10）：1⁃4．LI An，ZHANG Yun⁃dian．Stress analysis of quartz flexible accelerometer's chip components［J］．Journal of Mechanical＆Electrical Engineering，2010，27（10）：1⁃4．

［8］王春爱，蔡体菁．挠性加速度计石英摆片的力学分析［J］．舰船电子工程，2009，29（3）：56⁃60．WANG Chun⁃ai，CAI Ti⁃jing．Mechanical analysis of flex accelerometer's quartz chip［J］．Ship Electronic Engineer⁃ing，2009，29（3）：56⁃60．

［9］Yu X T，Zhang L，Guo L R，et al．Identification for tem⁃perature model of accelerometer based on proximal SVR and particle swarm optimization algorithms［J］．Control Theory and Technology，2012，10（3）：349⁃353．

Analysis on Scale Factor of Quartz Flexible Accelerometer Affected by Air Pressure

HUANG Li⁃juan，LV Jiang⁃tao，ZHENG Yong⁃qiang
（Designing Institute of Hubei Space Technology Academy，Wuhan 430040）

The quartz flexible accelerometers are one of the core devices，and they mainly measure accelerate of mov⁃ing vehicles to provide position information for system．Because of the force sensitive properties，accelerometer is easily af⁃fected by external environment．Through analysis of all of the environment factors affecting the scale factor of accelerometer in different places，such as time drift，temperature variation，shape change，this paper proposes that the main reason of which is the change of air pressure．Based on the principle of quartz flexible accelerometer and the force analysis of quartz pendulous reed，this paper analyzes the mechanism in detail about the change of air pressure leading to the change of accel⁃erometer scale factor，and givens in a formula to calculate the change value．A verification test proves the analysis and the formula in this paper to be correct．This conclusion in this paper can provide a reference to optimizing quartz flexible accel⁃erometer．It possesses a high value in engineering．

accelerometer；scale factor；influence of air pressure；theoretical analysis；experimental verification

TP21

A

1674⁃5558（2016）02⁃01247

10．3969／j．issn．1674⁃5558．2016．06．012

2016⁃03⁃06

黄丽娟，女，硕士，高级工程师，研究方向为飞行器惯性导航系统的设计与应用。